우리는 [호몰로지 대수학] §Ext와 Tor, ⁋정의 2에서 $\Tor$ functor들을 정의했으며, 만일 $B$가 flat $A$-algebra라면, 다음의 canonical isomorphism
\[B\otimes_A\Tor_i^A(M,N)\cong\Tor_i^B(B\otimes_AM, B\otimes_AN)\]이 존재한다는 것을 보았다. 이는 특히 $B=S^{-1}A$인 경우 잘 적용된다.
명제 1 $A$-module $M$과 $A$의 ideal $\mathfrak{a}$가 주어졌다 하자. 그럼 multiplication map $\mathfrak{a}\otimes_AM \rightarrow M$이 injection인 것과 $\Tor_1^A(A/\mathfrak{a}, M)=0$인 것이 동치이다. $M$이 flat인 것은 모든 finitely generated $\mathfrak{a}$에 대하여 $\mathfrak{a}\otimes_AM \rightarrow M$이 injection인 것과 동치이다.
증명
Short exact sequence
\[0 \rightarrow \mathfrak{a} \rightarrow A \rightarrow A/\mathfrak{a} \rightarrow 0\]에 $\Tor$ long exact sequence를 취하면
\[\cdots \rightarrow \Tor_1^A(A, M) \rightarrow \Tor_1^A(A/\mathfrak{a}, M) \rightarrow \mathfrak{a}\otimes_AM \rightarrow A\otimes_AM \rightarrow (A/\mathfrak{a})\otimes_AM \rightarrow 0\]을 얻는다. 이로부터 $\mathfrak{a}\otimes M \rightarrow M$이 injection인 것과 $\Tor_1^A(A/\mathfrak{a},M)=0$인 것이 동치인 것은 자명하다.
이제 두 번째 주장을 보여야 한다. 이를 위해서는 임의의 injection $L \rightarrow N$에 대하여, $L\otimes_AM \rightarrow N\otimes_AM$이 injection이 된다는 것을 보여야 한다. 그런데 이를 보이기 위해서는 $N$이 finitely generated임을 가정해도 충분하다. 임의의 $z\in N\otimes_AM$은 $x\otimes y$ 꼴의 원소들의 유한한 합으로 적히므로, 이러한 $x$들을 모아 만들어진 finitely generated module $N’$에 대해, $z$가 $N’\otimes_A M$의 원소라고 가정하여도 되기 때문이다.
이제 두 finitely generated $A$-module $N$, $L$ 사이에 있는 submodule들의 sequence
\[L=N_0 \subseteq N_1\subseteq\cdots\subseteq N_p=N\]을 잡아서, $N_{i+1}/N_i$들 각각이 하나의 원소로 생성되도록 할 수 있다. 그럼 $A$의 적당한 ideal $\mathfrak{a}$가 존재하여 $N_{i+1}/N_i\cong A/\mathfrak{a}$이다. 또, 이들 inclusion들을 반복하여 $L\hookrightarrow N$을 얻으면 이 또한 injection이므로, 결과적으로 $p=1$로 가정하고 $N/L\cong A/\mathfrak{a}$로 가정해도 충분하다. 위의 논의에 의하여, 임의의 finitely generated ideal $\mathfrak{a}’$에 대해 $\mathfrak{a}’\otimes_AM \rightarrow M$이 injection이라면 이 조건은 임의의 ideal $\mathfrak{a}$에 대해서도 $\mathfrak{a}\otimes_AM \rightarrow M$이 injection이 되는 것을 보이는 것도 기억하자. 이제 다음의 short exact sequence
\[0 \rightarrow L \rightarrow N \rightarrow N/L \rightarrow 0\]에 $\Tor$ long exact sequence를 취하면
\[\cdots \rightarrow \Tor_1^A(N/L, M) \rightarrow L\otimes_AM \rightarrow N\otimes_AM \rightarrow (N/L)\otimes_AM \rightarrow 0\]를 얻는데, 여기서 $\Tor_1^A(N/L,M)=\Tor_1^A(A/\mathfrak{a},M)$는 $0$이므로 원하는 결과를 얻는다.
이로부터, 특별한 몇몇 경우에 다음 따름정리들을 얻는다.
따름정리 2 Field $\mathbb{K}$와 ring $A=\mathbb{K}[t]/(t^2)$, 그리고 $A$-module $M$이 주어졌다 하자. 그럼 $M$이 flat $A$-module인 것과, multiplication $\times t: M \rightarrow tM$이 isomorphism $M/tM \rightarrow tM$을 유도하는 것이 동치이다.
증명
$A$의 유일한 ideal이 $(t)$이므로, $M$이 flat인 것은 $(t)\otimes_A M \rightarrow M$이 injective인 것과 동치이다. 한편, $\times t: A \rightarrow (t)$는 $A$-linear map이고, 그 kernel이 $(t)$이다. 더 명시적으로 이 $A$-linear isomorphism은 다음 식
\[A/(t)\cong \mathbb{K} \rightarrow (t);\qquad a+(t)\mapsto at\]으로 주어진다. 이제 이로부터 isomorphism
\[M/tM\cong A/(t)\otimes_A M \cong (t)\otimes_A M\]을 얻는다. 한편 multiplication map $(t)\otimes_AM \rightarrow M$은 $A$-bilinear map
\[(t)\times M \rightarrow M;\qquad (ta, x)\mapsto (ta)x\]을 통해 얻어지는 것이며, 이를 위의 isomorphism과 합성하면 그로부터 얻어지는 $M/tM \rightarrow M$은 임의의 $x+tM\in M/tM$에 대하여,
\[x+tM \mapsto (1+(t))\otimes x\mapsto t\otimes x\mapsto tx\]으로 얻어진다. 즉, $M/tM \rightarrow M$이 정확히 $t$를 곱하여 얻어지는 함수 $tM$이며, 이 함수의 image가 $tM$인 것은 자명하므로, $\times t: M/tM \rightarrow tM$이 isomorphism인 것과 $(t)\otimes_AM \rightarrow M$이 injective인 것이 동치이고, 이는 다시 명제 1에 의해 $M$이 flat인 것과 동치이다.
따름정리 3 Zero-divisor가 아닌 원소 $a\in A$를 고정하자. 만일 $M$이 flat $A$-module이라면, $a$는 $M$의 zero-divisor가 아니다. 만일 $A$가 PID라면 그 역도 성립한다.
증명
$M$이 flat $A$-module이라면 $(a)\otimes_AM \rightarrow M$이 injection이므로 $a$는 $M$의 non-zerodivisor이다. 한편 $A$가 PID라면, $A$의 모든 ideal이 non-zerodivisor 하나로 생성되고, 특히 모든 ideal $\mathfrak{a}$에 대하여 $\mathfrak{a}\otimes_AM \rightarrow M$이 injective이다.
일반적으로 tensor product의 원소를 표현하는 방식은 유일하지 않다. 다음 보조정리는 이를 어느정도 해소해준다.
보조정리 4 두 $A$-module $M,N$을 고정하고, $N$이 $\{y_j\}_{j\in J}$들로 생성된다 하자. 이제 $M\otimes_AN$의 임의의 원소를 유한합
\[\sum_{j\in J} x_j\otimes y_j\]으로 나타냈을 때, 이 원소가 $0$이 되는 것과, 적당한 $M$의 원소들 $\{x_j’\}_{j\in J}$, index set $I$, 그리고 $a_{ij}\in A$가 존재하여 다음 식
\[\sum_{i\in I} a_{ij}x_i'=x_j\quad\text{for all $j$},\qquad \sum_{j\in J} a_{ij}y_j=0\quad\text{for all $i$}\]이 성립하는 것이 동치이다.
증명
우선 주어진 조건을 만족하는 $x_j’$들과 $a_{ij}$들이 모두 존재한다 하면
\[\sum_{j\in J} x_j\otimes y_j=\sum_{j\in J}\left(\left(\sum_{i\in I}a_{ij}x_i'\right)\otimes y_j\right)=\sum_{i\in I} x_i'\otimes\left(\sum_{j\in J} a_{ij} y_j\right)=0\]이 되므로 역방향은 쉽게 얻어진다.
이제 원래의 방향을 보이기 위해 먼저 $N$이 free module익고 $\{y_j\}_{j\in J}$가 $N$의 basis인 경우를 살펴보자. 그럼 다음의 isomorphism
\[M\otimes_AN\cong\bigoplus_{j\in J} (M\otimes_A Ay_j)\cong \bigoplus_{j\in J} M\]을 생각하면 ([대수적 구조] §가군의 직접곱과 직합, 텐서곱, ⁋정리 6), 원소 $\sum_j x_j\otimes y_j$는 $(x_j)_{j\in J}$에 해당되므로 이 원소가 $0$인 것과 모든 $x_j$가 $0$인 것이 동치이다.
이제 임의의 module $N$에 대하여, 적당한 free $A$-module $F$, $\varepsilon: F \rightarrow N$을 택하여 $F$의 basis $\{f_j\}_{j\in J}$가 $\varepsilon$을 통해 $\{y_j\}_{j\in J}$로 옮겨지도록 할 수 있다. ([다중선형대수학] §기저, ⁋정의 1) 그럼 다음의 short exact sequence
\[0 \longrightarrow\ker\varepsilon \longrightarrow F \overset{\varepsilon}{\longrightarrow} N \longrightarrow 0\]를 얻으며, 다시 $\ker \varepsilon$을 [다중선형대수학] §기저, ⁋명제 2를 통해 free module $G$의 quotient로 보면 다음의 exact sequence
\[G \rightarrow \ker\varepsilon \rightarrow 0\]를 얻는다. 이들을 통해 $N$의 free presentation
\[G \overset{\eta}{\longrightarrow} F \overset{\varepsilon}{\longrightarrow} N \longrightarrow 0\]을 얻는다. 한편 $M\otimes_A-$는 right exact이므로, 이로부터 다음의 exact sequence
\[M\otimes_A G \overset{\id_M\otimes\eta}{\longrightarrow} M\otimes_AF \overset{\id_M\otimes \varepsilon}{\longrightarrow} M\otimes_AN \longrightarrow 0\]을 얻으며, 가정에 의해 $\sum_{j\in J} x_j\otimes f_j$는 $\id_M\otimes\varepsilon$을 통해 $0$으로 보내진다. 따라서, $M\otimes_AF$에서의 exactness로부터 적당한 $x_i’\in M$, $z_i\in G$들을 택하여
\[\sum_{i\in I} x_i'\otimes\eta(z_i)=(\id_M\otimes\eta)\left(\sum_i x_i'\otimes z_i\right)=\sum_j x_j\otimes f_j\]이도록 할 수 있다. 한편 $F$의 basis $\{f_j\}_{j\in J}$를 이용하여
\[\eta(z_i)=\sum_{j\in J} a_{ij}f_j,\qquad\text{$(a_{ij})_{j\in J}$ finitely supported for all $i$}\]로 적을 수 있다. 이를 위의 식에 대입하면
\[\sum_{j\in J} x_j\otimes f_j=\sum_{i\in I} x_i'\otimes\eta(z_i)=\sum_{i\in I}\sum_{j\in J}a_{ij}x_i'\otimes f_j\]으로부터
\[0=\sum_{j\in J} x_j \otimes f_j-\sum_{i\in I}\sum_{j\in J} a_{ij}x_i'\otimes f_j=\sum_{j\in J} \left(x_j-\sum_{i\in I} a_{ij}x_i'\right)\otimes f_j\]을 얻고, 따라서 위에서 보인 free module일 때의 결과에 의해 $x_j=\sum_{i\in I} a_{ij}x_i’$인 것을 안다. 이 때 $\eta(z_i)$의 $\varepsilon$에 의한 image를 생각하면
\[0=(\varepsilon\circ\eta)(z_i)=\varepsilon\left(\sum_{j\in J} a_{ij}f_j\right)=\sum_{j\in J} a_{ij}y_j\]이므로 원하는 결과를 얻는다.
더 일반적으로 다음이 성립한다.
따름정리 5 $A$-module $M$이 flat인 것과 다음 조건이 동치이다.
$0=\sum_{i\in I} a_ix_i$를 만족하는 $x_i\in M$과 $a_i\in A$가 주어질 때마다 index set $J$, $x_j’\in M$, $b_{ij}\in A$들이 존재하여 다음 두 식
\[\sum_{j\in J} b_{ij} x_j'=x_i\quad\text{for all $i$},\qquad \sum_{i\in I} b_{ij} a_i=0\quad\text{for all $j$}\]을 만족한다.
증명
명제 1의 결과로부터, $M$이 flat인 것과 임의의 finitely generated ideal $\mathfrak{a}$에 대해 multiplication map
\[\mathfrak{a}\otimes_A M \rightarrow M\]이 injective인 것과 동치이다. 이는
\[\sum_i a_i\otimes x_i\in \mathfrak{a}\otimes_AM\]이 위의 multiplication map의 kernel에 속한다면 이 원소가 반드시 $0$이 되어야 한다는 것과 동치이며, 이제 보조정리 4를 이용하여 이 원소가 언제 $0$이 되는지를 살펴보면 원하는 결과를 얻는다.
한편 flatness 또한 [호몰로지 대수학] §분해, ⁋정의 1과 비슷한 형태로 diagram의 언어를 이용해 서술할 수 있다.
따름정리 6 $A$-module $M$에 대하여 다음이 모두 동치이다.
- $M$이 flat $A$-module이다.
-
임의의 finitely generated free module $F$, morphism $u:F \rightarrow M$과 $\ker u$의 monogeneous submodule $K$에 대하여, 다음 diagram
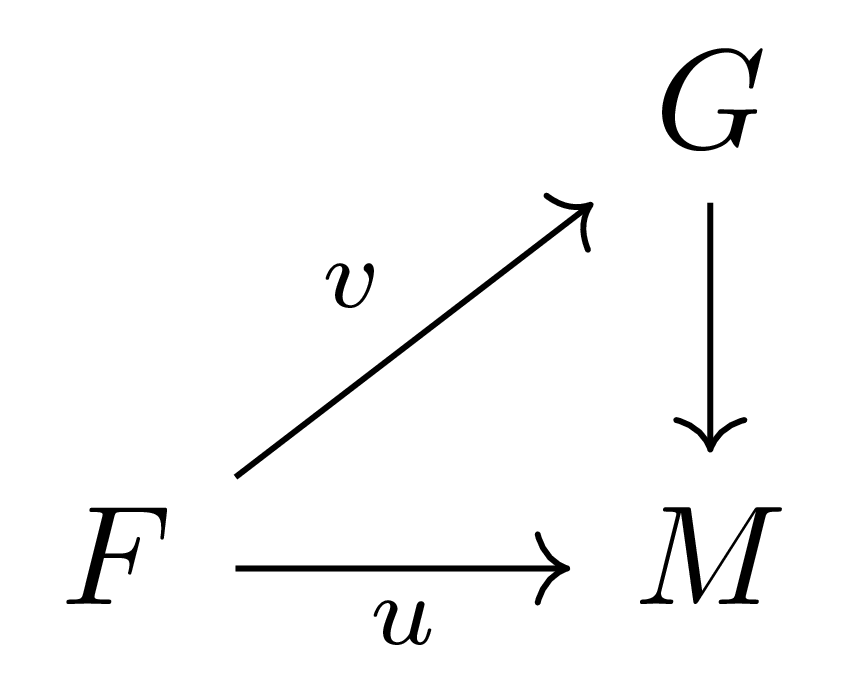
이 존재하여 $K\subseteq \ker v$이도록 할 수 있다.
- 2번 조건은 가정을 $\ker u$의 monogeneous submodule 대신 finitely generated submodule로 약화시켜도 성립한다.
증명
첫 번째와 두 번째 조건이 동치인 것은 따름정리 5에 의해 자명하다. 따라서 둘째 조건을 가정하고 셋째 조건만 보이면 충분한데, 이는 $K$의 generator들 $x_1,\ldots, x_n$에 대하여 monogenous submodule $x_1$를 죽이는 $v_1:F \rightarrow G$를 택한 후, $v_1(K)$의 남은 generator들 $v_1(x_2),\ldots, v_1(x_n)$에 같은 과정을 반복하면 된다.
만일 $M$이 finitely presented라면, 다음의 exact sequence
\[0 \rightarrow K \rightarrow F \rightarrow M \rightarrow 0\]이 존재한다. 여기서 $F$는 finitely generated free $A$-module이고, $K$ 또한 finitely generated이다. 만일 $M$이 flat이라면, 위의 따름정리에서 $\im v\subseteq G$는 $G \rightarrow M$에 의하여 $M$으로 isomorphic하게 옮겨진다. 따라서 $G \rightarrow M$이 split하고, 이로부터 $M$이 $G$의 direct summand인 것을 안다. 즉, finitely presented flat module은 finitely presented projective module과 같은 것이다. ([다중선형대수학] §사영가군, 단사가군, 평탄가군, ⁋명제 4)
따름정리 7 Field $\mathbb{K}$와 $A=\mathbb{K}[\x]$를 고정하고, $E$가 flat $A$-algebra라 하자. 만일 $E/\x E$가 domain이고, $S$가 $f\in E$에 대해 $1-\x f$ 꼴의 원소들의 모임이라면 $S^{-1}E$는 domain이다.
증명
우선 주어진 명제를 간단한 형태로 바꾸자. Localization을 취하는 것은 $\otimes$를 보존하므로, $E$를 $S^{-1}E$로 바꾸어도 $S^{-1}E$는 여전히 flat $A$-algebra이다. 또, $E/\x E$가 domain이라면 $S^{-1} E/ \x S^{-1}E$ 또한 domain이므로, 처음부터 $E$를 $S^{-1}E$로 택해도 된다. 이 때, $S$를 조건과 같이 선택하는 것은 $E$의 $1-\x f$ 꼴의 모든 원소가 unit이라는 가정으로 바꿔줄 수 있다.
이제 위의 조건 하에서 $E$의 ideal들 $\mathfrak{a}, \mathfrak{b}$가 $\mathfrak{a}\mathfrak{b}=0$을 만족한다 하고, $\mathfrak{a}=0$ 혹은 $\mathfrak{b}=0$이 성립해야 한다는 것을 보여야 한다. 그럼 $\mathfrak{a}\mathfrak{b}=0$이므로, 필요하다면 $\mathfrak{a}$와 $\mathfrak{b}$를 키워서 이들이 서로의 annihilator라고 가정할 수 있다. 이제 $\mathfrak{a}\mathfrak{b}=0$ modulo $\x$이고, $E/\x E$가 domain이므로 $\mathfrak{b}\subseteq (\x)$라 가정할 수 있다. 그럼 $\x$는 $E$의 non-zerodivisor이고 $\mathfrak{a}(\mathfrak{b}:(\x))\x=0$이므로 $(\mathfrak{b}:(\x))$는 $\mathfrak{a}$를 annihilate한다. 즉, $(\mathfrak{b}:(\x))\subseteq \mathfrak{b}$이므로 $\mathfrak{b}=\x\mathfrak{b}$이다. 이제 §정수적 확장, ⁋보조정리 7으로부터 원하는 결과를 얻는다.
참고문헌
[Eis] David Eisenbud. Commutative Algebra: with a view toward algebraic geometry. Springer, 1995.

댓글남기기