인자 - Blackbox

이번 글에서 우리는 §분수아이디얼, ⁋정의 4에서 정의한 $\CaDiv(A)$와 $\Pic(A)$에 대해 조금 더 자세히 살펴본다.

데데킨트 정역

우선 다음을 정의하자.

정의 1 Ring $A$의 ideal $\mathfrak{a}$가 pure codimension $1$이라는 것은 $\mathfrak{a}$의 임의의 associated prime ideal이 codimension $1$인 것이다.

특별히 $\mathfrak{a}=A$인 경우 associated prime ideal이 존재하지 않으므로, 이 경우에 $A$는 vacuous하게 codimension $1$을 갖는다. 그럼 다음이 성립한다.

정리 2 Noetherian integral domain $A$에 대하여, $A$의 maximal ideal에서의 localization $A_\mathfrak{m}$이 항상 UFD라 하자.

임의의 ideal $\mathfrak{a}\subseteq A$가 invertible인 것은 $\mathfrak{a}$가 pure codimension $1$인 것과 동치이다.
임의의 invertible fractional ideal $\mathfrak{A}\subseteq K$는 codimension $1$짜리 prime ideal들의 유한한 곱으로 유일하게 나타낼 수 있으며, 따라서 $\CaDiv(A)$는 codimension $1$의 prime ideal들로 생성되는 free abelian group이 된다.

증명

우선 $\mathfrak{a}$가 invertible이라 가정하자. 그럼 우선 $\mathfrak{a}$를 임의의 maximal ideal $\mathfrak{m}$에서 localize하여 얻어지는 $\mathfrak{a}A_\mathfrak{m}$은, $A_\mathfrak{m}$을 $\Frac(A)$에 속한 것으로 보면, $K$의 non-zerodivisor로 생성되는 principal ideal이다. 한편 임의의 maximal ideal $\mathfrak{m}\subseteq A$에 대해 $\mathfrak{A}_\mathfrak{m}$은 §정수적 확장, ⁋명제 9에 의하여 임의의 normal domain이므로, §정칙국소환, ⁋정리 8을 적용하면 principal ideal $\mathfrak{a}A_\mathfrak{m}$의 associated prime ideal $\mathfrak{p}A_\mathfrak{m}$에 대하여,
\[(\mathfrak{p}A_\mathfrak{m})(A_\mathfrak{m})_{\mathfrak{p}A_\mathfrak{m}}\cong \mathfrak{p}A_\mathfrak{p}\]
는 $(A_\mathfrak{m})_{\mathfrak{p}A_\mathfrak{m}}\cong A_\mathfrak{p}$에서의 principal ideal이고 따라서
\[\codim \mathfrak{p}=\dim A_\mathfrak{p}=\codim \mathfrak{p}A_\mathfrak{p}\leq 1\]
인데, $A_\mathfrak{p}$는 integral domain이므로 $(0)\subseteq \mathfrak{p}A_\mathfrak{p}$로부터 $\codim \mathfrak{p}=1$인 것을 안다.

거꾸로 $\mathfrak{a}$가 pure codimension $1$이라 가정하고 invertible임을 보이자.
우선 주장의 조건 하에서, $A$의 임의의 codimension $1$ prime ideal $\mathfrak{p}$는 invertible이다. 이는 우선, 만일 $\mathfrak{p}\not\subset \mathfrak{m}$일 경우 $\mathfrak{p}A_\mathfrak{m}=A_\mathfrak{m}$이 되고, 만일 $\mathfrak{p}\subseteq \mathfrak{m}$일 경우 위의 계산에 의해 $\mathfrak{p}A_\mathfrak{m}$은 $A_\mathfrak{m}$의 codimension $1$ prime ideal이며, $A_\mathfrak{m}$은 domain이므로 minimal prime ideal이고, 따라서 §차원, ⁋따름정리 8을 적용하면 principal ideal이 되어 invertible하다. 이제 invertible module들의 곱은 다시 invertible이므로, 우리는 $\mathfrak{A}$가 codimension $1$ prime ideal들의 곱이라는 것만 보이면 충분하다.
결론에 반하여 pure codimension $1$이지만 codimension $1$ prime ideal들의 곱으로 나타나지 않는 ideal이 존재한다 하고, $\mathfrak{A}$가 이러한 ideal들 중 maximal한 것이라 하자. $\mathfrak{p}$가 $\mathfrak{A}$를 포함하는 codimension $1$ prime ideal이라면, $\mathfrak{p}^{-1}\mathfrak{p}=A$이고 따라서 $A\subsetneq\mathfrak{p}^{-1}$이다. 이제 만일 $\mathfrak{p}^{-1}\mathfrak{A}=\mathfrak{A}$라면, §정수적 확장, ⁋보조정리 5에 의하여 $\mathfrak{p}^{-1}$의 원소들은 $A$에 대해 integral이다. 그런데 §정수적 확장, ⁋명제 9에 의해 $A$는 normal이므로 이는 불가능하고 따라서 $\mathfrak{A}\subsetneq \mathfrak{p}^{-1}\mathfrak{A}$여야 한다. 이제 $\mathfrak{A}$의 maximality로부터, $\mathfrak{p}^{-1}\mathfrak{A}$는 codimension $1$ prime ideal들의 곱으로 나타낼 수 있고, 양 변에 $\mathfrak{p}$를 곱해주면 모순이므로 원하는 결과를 얻는다. 이 표현의 유일성은 귀납법을 통해 보일 수 있으며, §분수아이디얼, ⁋따름정리 5를 적용하면 $\CaDiv(A)$가 codimension $1$ prime ideal들로 생성되는 것을 안다.

정의 3 Noetherian normal domain of dimension $1$을 Dedekind domain_{데데킨트 정역}이라 부른다.

그럼 다음이 성립한다.

따름정리 4 Dedekind domain $A$의 임의의 아이디얼은 invertible하며, prime ideal들의 곱으로 유일하게 표현할 수 있으며, $A$의 fractional ideal도 마찬가지이다. 따라서 $\CaDiv(A)$는 $A$의 maximal ideal로 생성되는 free abelian group이 된다.

§분수아이디얼, ⁋따름정리 5에 의하여 우리는 $\Pic(A)\cong \CaDiv(A)/K^\ast$임을 안다. Dedekind domain은 주로 대수적 정수론에서 많이 사용되는데, 해당 분야에서의 용어를 사용하여, $A$가 Dedekind domain일 때는 $\Pic(A)$를 class group_유군이라 부른다.

인자

따름정리 4는 UFD에서 임의의 원소를 irreducible element들의 곱으로 유일하게 표현할 수 있듯이, Dedekind domain에서는 임의의 ideal을 codimension $1$ prime ideal들의 곱으로 유일하게 표현할 수 있고, fractional ideal들은 여기에 음의 거듭제곱을 포함하여 표현할 수 있다는 것을 보여준다. 우리는 이를 더 일반화하여, 임의의 ring $A$에 대하여 다음을 정의한다.

정의 5 Ring $A$의 Weil divisor_{베유 인자}는 $A$의 codimension $1$ prime ideal들로 생성되는 free abelian group $\Div(A)$의 원소를 뜻한다.

$\Div(A)$의 연산은 $+$로 표기하는 것이 관례이다. 그럼 $\Div(A)$의 원소는 codimension $1$ prime ideal들의 formal linear combination이다.

정리 6 Noetherian ring $A$를 고정하자. 그럼 모든 invertible ideal $\mathfrak{a}$에 대하여

\[\mathfrak{a}\mapsto \sum_\text{\scriptsize$\mathfrak{p}\subseteq A$ a codimension $1$ prime} \length(A_\mathfrak{p}/\mathfrak{a}A_\mathfrak{p}) \mathfrak{p}\]

을 만족하는 group homomorphism $\Phi: \CaDiv(A) \rightarrow \Div(A)$가 존재한다.

증명

§분수아이디얼, ⁋따름정리 5와 free abelian group의 universal property로부터, 우리는 위의 식이 잘 정의되고, ideal product를 보존함을 보이면 충분하다.

우선 위의 식이 잘 정의됨을 보이자. 즉 임의의 invertible ideal $\mathfrak{a}$에 대하여 주어진 식이 유한합임을 보여야 한다. 임의의 codimension $1$ prime ideal $\mathfrak{p}$에 대하여, 1차원 local ring $A_\mathfrak{p}$를 보자. 그럼 §분수아이디얼, ⁋정리 3에 의해 $\mathfrak{a}$는 $A$의 non-zerodivisor를 포함하고, 따라서 $\mathfrak{a}A_\mathfrak{p}$도 $A_\mathfrak{p}$의 non-zerodivisor $a$를 포함한다. 한편 $\dim A_\mathfrak{p}=\codim \mathfrak{p}A_\mathfrak{p}$는 $\mathfrak{p}A_\mathfrak{p}$에 포함되는 ideal의 codimension보다는 항상 같거나 클 것이므로,

\[\dim \mathfrak{a}A_\mathfrak{p}\leq\dim \mathfrak{p}A_\mathfrak{p}\leq \dim A_\mathfrak{p}-\codim \mathfrak{p}A_\mathfrak{p}\]

이고, $\mathfrak{p}A_\mathfrak{p}$는 non-zerodivisor를 포함하므로 $\codim \mathfrak{p}A_\mathfrak{p}=1$가 되어 $\dim \mathfrak{a}A_\mathfrak{p}=0$이다. 이로부터 §차원, ⁋따름정리 3 그리고 §조르단-횔더 정리, ⁋정리 3에 의하여 $\length(A_\mathfrak{p}/\mathfrak{a}A_\mathfrak{p})<\infty$임을 안다.

이제 $\mathfrak{a}\subsetneq \mathfrak{p}$인 경우, $\mathfrak{a}A_\mathfrak{p}$는 $A_\mathfrak{p}$의 unit을 포함하므로 $\mathfrak{a}A_\mathfrak{p}=A_\mathfrak{p}$이고 따라서 $\length(A_\mathfrak{p}/\mathfrak{a}A_\mathfrak{p})=0$이다. 또, 만일 $\mathfrak{a}\subsetneq \mathfrak{p}$인 경우, $\mathfrak{p}A_\mathfrak{p}$는 $\mathfrak{a}A_\mathfrak{p}$를 포함하는 minimal prime ideal 중 하나가 되어야 하고, 따라서 이를 만족하는 $\mathfrak{p}$는 $\mathfrak{a}$가 주어질 때마다 오직 유한히 많게 고정된다. 이상의 논의로부터 주어진 식이 잘 정의됨을 확인할 수 있다.

이제 $\Phi$가 곱셈을 잘 보존하는 것을 보여야 한다. 즉, 만일 $\mathfrak{a}=\prod \mathfrak{a}_i$라면, 다음의 식

\[\length(A_\mathfrak{p}/\mathfrak{a}A_\mathfrak{p})=\sum \length(A_\mathfrak{p}/\mathfrak{a}_iA_\mathfrak{p})\]

이 성립하는 것을 보여야 한다. 표기의 편의를 위해, localization을 하여 얻어진 local ring을 $A$, 그 maximal ideal을 $\mathfrak{p}$, 그리고 $\mathfrak{a}_i$들은 $A$의 ideal들이라 하자. 그럼 $\mathfrak{a}_i$가 invertible ideal이므로, 이들은 하나의 non-zerodivisor $a_i$로 생성되고 그럼 다음의 filtration

\[A\supseteq \mathfrak{a}_1=(a_1)\supseteq \mathfrak{a}_1 \mathfrak{a}_2=(a_1a_2)\supseteq\cdots\supseteq \prod_{i\in I} \mathfrak{a}_i=\left(\prod_{i\in I} a_i\right)\]

이 존재한다. 이제 주어진 식을 보이기 위해서는 $(\prod_{j< i}a_j)/(\prod_{j\leq i} a_j)\cong A/(a_i)$를 보이면 충분하다. 이는 각각의 $a_i$가 non-zerodivisor이므로, $\prod_{j< i}a_j$를 곱하는 것이 $A$에서 $(\prod_{j< i}a_j)$로의 isomorphism을 유도하고, 이 때 다음의 map

\[(\prod_{j< i}a_j) \rightarrow A \rightarrow A/(A_i)\]

의 kernel을 생각하면 이것이 정확히 $(a_i\prod_{j< i}a_j)=(\prod_{j\leq i}a_j)$가 되므로 자명하다.

특별히 만일 $A$가 $1$차원이었다면, §조르단-횔더 정리, ⁋정리 3의 둘째 결과의 계산에 의하여

\[\length A/\mathfrak{a}=\sum_\text{\scriptsize$\mathfrak{p}\subseteq \mathfrak{a}$ a codimension $1 prime of $A$} \length (A_\mathfrak{p}/\mathfrak{a}A_\mathfrak{p})\]

이 성립하고, 따라서 $\Div(A) \rightarrow \mathbb{Z}$를 $\sum n_\mathfrak{p}\mathfrak{p}\mapsto \sum n_\mathfrak{p}$로 정의하면 정리 6에서의 map과의 합성을 통해 식 $\mathfrak{a}\mapsto \length(A/\mathfrak{a})$를 만족하는 $\CaDiv(A)$에서 $\mathbb{Z}$로의 map이 존재함을 안다.

한편 우리는 $\CaDiv(A)$ 위에 적절한 equivalence relation을 주어 정의한 $\CaDiv(A)$의 원소들의 equivalence class들의 모임을 $\Pic(A)$로 적을 수 있었다. 비슷한 맥락에서 다음을 정의한다.

정의 7 Noetherian ring $A$와 $A$의 total ring of fractions $K$가 주어졌다 하자. 그럼 임의의 $a\in K^\times$에 대하여, invertible ideal $(a)$의 $\Phi:\CaDiv(A) \rightarrow \Div(A)$에 의한 image를 principal divisor_주인자라 부른다.
$A$의 principal divisor들의 group $\Prin(A)\subseteq \Div(A)$에 대하여, quotient group $\Div(A)/\Prin(A)$를 $A$의 codimension $1$ Chow group_{저우 군}이라 부르고 $\Chow(A)$로 표기한다.

그럼 정의로부터 $\Phi:\CaDiv(A) \rightarrow \Div(A)$가 $\Psi: \Pic(A) \rightarrow \Chow(A)$를 유도하는 것을 안다.

차원과 정규화

우리는 위에서 group homomorphism $\Phi:\CaDiv(A) \rightarrow \Div(A)$와 이로부터 얻어지는 group homomorphism $\Psi:\Pic(A) \rightarrow \Chow(A)$를 정의하였다. 한편 $\Phi$

정의 8 Reduced ring $A$에 대하여, $A$의 normalization_정규화은 $A$의 total ring of fractions $K$에서의 $A$의 integral closure이다. 만일 $A$의 normalization이 자기자신이라면, $A$를 normal ring_정규환이라 부른다.

만일 $A$가 integral domain이었다면 $K=\Frac(A)$이고 따라서 이 경우의 normalization과 normal ring의 개념은 §정수적 확장, ⁋정의 3에서 정의한 것과 동일하다. 그럼 다음이 성립한다.

명제 9 Normal noetherian ring $A$에 대하여, 위에서 정의한 $\Phi,\Psi$는 모두 injective이다.

증명

다음의 diagram

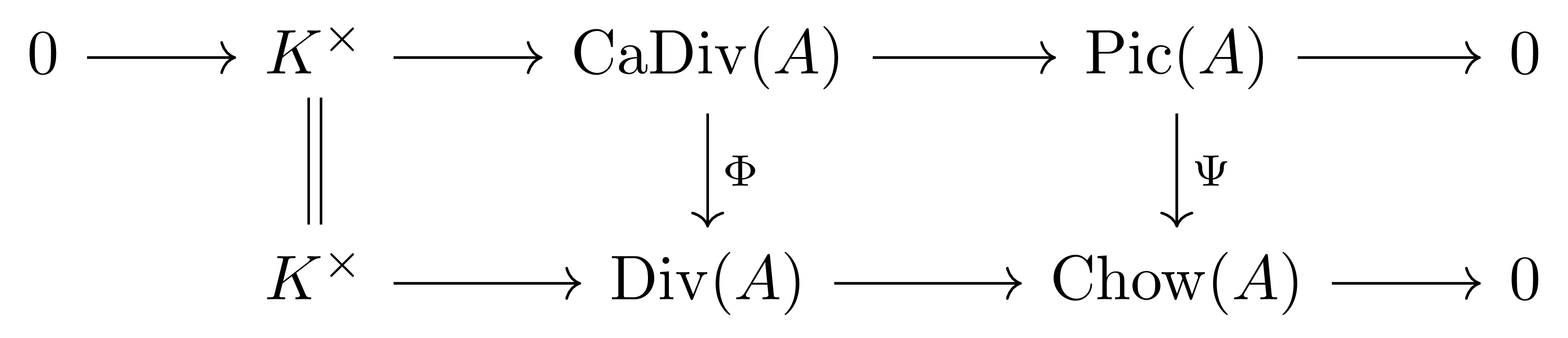
$relations_between_divisors$

을 생각하면, [호몰로지 대수학] §Diagram chasing, ⁋명제 1에 의해 $\Phi$가 injective인 것만 보이면 충분하다. 즉, $A$의 두 invertible ideal이 $\Phi$를 통해 $\Div(A)$의 같은 원소로 보내진다면 이들이 동일하다는 것을 증명하면 충분하다.

따라서 두 invertible ideal $\mathfrak{a}, \mathfrak{b}$이 $\Phi(\mathfrak{a})=\Phi(\mathfrak{b})$를 만족한다 하고 $\mathfrak{a}=\mathfrak{b}$임을 보이자. 대칭성에 의해 $\mathfrak{a}\subseteq \mathfrak{b}$임을 보이면 충분하며, §동반소아이디얼, ⁋따름정리 3의 결과에 의하여 이는 다시 $\mathfrak{a}A_\mathfrak{p}\subseteq \mathfrak{b}A_\mathfrak{p}$가 모든 associated prime $\mathfrak{p}$에 대해 성립함을 보이면 충분하다. 그런데 이제 $\mathfrak{p}A_\mathfrak{p}$는 $\mathfrak{b}A_\mathfrak{p}$의 associated prime이고, $\mathfrak{b}A_\mathfrak{p}$는 non-zerodivisor로 생성되는 principal ideal이므로 §정칙국소환, ⁋정리 10의 동치에 의해 $\codim \mathfrak{p}=1$이고 $A_\mathfrak{p}$는 DVR이다. 이제 $\Phi(\mathfrak{a})=\Phi(\mathfrak{b})$인 것으로부터 $\length(A_\mathfrak{p}/\mathfrak{a}A_\mathfrak{p})=\length(A_\mathfrak{p}/\mathfrak{b}A_\mathfrak{p})$이고 이로부터 $\mathfrak{a}A_\mathfrak{p}=\mathfrak{b}A_\mathfrak{p}$가 성립함을 안다.

크룰-아키즈키 정리

이제 남은 글에서 우리의 목표는 정리 11를 보이는 것이다. 이를 위해 다음의 보조정리를 보인다.

보조정리 10 1차원 noetherian ring $A$와 torsion-free $A$-module $M$이 주어졌다 하자. 그럼 임의의 $x\in A$에 대하여, 다음의 부등식

\[\length(M/xM)\leq \rank(M)\length(A/x)\]

이 성립하며, 등식은 $M$이 finitely generated $A$-module일 경우 성립한다.

증명

참고문헌

[Eis] David Eisenbud. Commutative Algebra: with a view toward algebraic geometry. Springer, 1995.

Twitter Facebook LinkedIn

인자

K

데데킨트 정역

인자

차원과 정규화

크룰-아키즈키 정리

공유하기

댓글남기기