이제 우리는 국소화의 추가적인 성질들에 대해 살펴본다. 이 글의 첫 번째 목표는 앞선 글에서 살펴본 가군의 국소화와 환의 국소화 사이에 밀접한 관계가 있다는 것을 증명하는 것이다. 이 글에서 ring $A$, $A$의 multiplicative subset $S$와 $A$-module $M$을 고정한다.
국소화와 Hom, tensor
우선 보조정리 하나를 증명하며 시작한다. $A$-module homomorphism $S^{-1}A\times_A M \rightarrow S^{-1}M$을 $(r/u, x)\mapsto rx/u$으로 정의하면 이는 $A$-bilinear map이고, 따라서 $A$-linear map $S^{-1}A\otimes_A M \rightarrow S^{-1}M$을 유도한다. ([대수적 구조] §가군의 직접곱과 직합, 텐서곱, ⁋정리 5)
보조정리 1 위에서 정의한 $A$-linear map은 isomorphism이 된다.
증명
역함수를 만들어주면 충분하다. 이를 위해 우선 $M\times S$에서 $S^{-1}A\otimes_AM$으로의 함수를
\[(x,s)\mapsto \frac{1}{s}\otimes x\]으로 정의하자. 그럼 이 함수는 $S^{-1}M$에서 $S^{-1}A\otimes_AM$으로의 잘 정의된 $A$-linear map을 정의한다. 이를 살펴보기 위해서는 이 함수가 $M\times S$ 위에 정의된 equivalence relation에 대해 잘 행동하는 것을 보이면 충분하다. 따라서 $(x,s)\sim (x’,s’)$를 만족하는 $M\times S$의 두 원소가 주어졌다 하자. 그럼 적당한 $t\in S$가 존재하여 $tsx’=ts’x$가 성립하며, 이로부터
\[\frac{1}{tss'}\otimes ts'x=\frac{1}{tss'}\otimes tsx'\]가 성립한다. 그런데 $ts’,ts\in A$이므로, 좌변과 우변의 $ts’$와 $ts$를 각각 $\otimes$의 왼쪽으로 넘겨주면
\[\frac{1}{s}\otimes x=\frac{1}{s'}\otimes x'\]를 얻는다. 이 함수가 $A$-linear map이며 위에서 정의한 $S^{-1}A\otimes_A M \rightarrow S^{-1}M$의 역함수임은 자명하다.
특히 이를 이용하여 module의 localization의 functoriality 또한 보일 수 있다. 임의의 $u: M \rightarrow M’$에 대하여 $S^{-1}M \rightarrow S^{-1}M’$을 다음 함수
\[S^{-1}\otimes_A u: S^{-1}\otimes_AM \rightarrow S^{-1}\otimes_AM'\]의 양 변을 localization과 동일시하여 정의하면 되기 때문이다. 일반적으로 텐서곱은 right exact이지만, 이 경우에는 exact functor가 된다.
명제 2 $S^{-1}A$는 flat $A$-module이다. ([다중선형대수학] §사영가군, 단사가군, 평탄가군, ⁋정의 7)
증명
임의의 injective $A$-linear map $u:M \rightarrow M’$이 주어졌다 하고, $S^{-1}A\otimes_A u$이 injective인 것을 보여야 한다. 그런데 보조정리 1에 의해, 이는 linear map $S^{-1}M \rightarrow S^{-1}M’$이 injective인 것을 보이면 충분하다. 어떠한 $x/s\in S^{-1}M$에 대하여, 이를 $S^{-1}M’$으로 보낸 원소인 $u(x)/s$가 $S^{-1}M’$에서 $0$이라 하자. 그럼 $u(x)/s=0/1$로부터 적당한 $t\in S$가 존재하여
\[tu(x)=u(tx)=0\]이 성립하고, $u$가 injective이므로 $M$에서 $tx=0$이어야 한다. 그럼 $S^{-1}M$에서
\[\frac{x}{s}=\frac{tx}{ts}=\frac{0}{ts}=0\]이므로 원하는 결과를 얻는다.
국소화에 의해 결정되는 성질들
위의 명제 2에 의하여, $u:M \rightarrow M’$이 injective (resp. surjective, bijective)라면 이로부터 유도되는 $S^{-1}M \rightarrow S^{-1}M’$ 또한 그러하다는 것을 안다. 명제 4는 이에 대한 일종의 (강력한) 역이라고 생각할 수 있다. 이를 위해 우선 다음 보조정리를 보인다.
보조정리 3 $A$-module $M$과, $A$의 maximal ideal $\mathfrak{m}$에서의 localization $\epsilon_\mathfrak{m}:M \rightarrow M_\mathfrak{m}$을 생각하자. 그럼 $M$의 원소 $x$가 $0$인 것은,
증명
한쪽 방향은 자명하므로 반대쪽만 보이면 충분하다. 고정된 maximal ideal $\mathfrak{m}$에 대하여 $\epsilon_\mathfrak{m}(x)=0$이 성립한다 하자. 이는 $\ann(x)$가 $\mathfrak{m}$에 포함되지 않는 것과 동치이다. 그럼 주어진 조건에 의하여, $\ann(x)$는
따라서 다음이 성립한다.
명제 4 $A$-linear map $u:M \rightarrow N$이 monomorphism (resp. epimorphism, isomorphism)인 것은 임의의 maximal ideal $\mathfrak{m}$에 대하여 $u_\mathfrak{m}: M_\mathfrak{m} \rightarrow N_\mathfrak{m}$이 그러한 것과 동치이다.
이에 대한 증명은 보조정리 3를 kernel과 cokernel에 대해 적용하면 충분하다.
다음 정리는 앞으로 종종 사용될 것이므로, 증명은 신경쓰지 않더라도 결과는 기억해두는 것이 좋다.
명제 5 Ring $A$와 $A$-algebra $E$를 고정하자. 그럼 임의의 $A$-module $M,N$에 대하여 다음의 $E$-module homomorphism
\[\alpha: E\otimes_A\Hom_A(M,N) \rightarrow\Hom_E(E\otimes_A M, E\otimes_AN);\qquad (1\otimes f)\mapsto \id_E\otimes_A f\]이 잘 정의된다. 특히 만일 $E$가 flat $A$-module이고 $M$이 finitely presented라면 $\alpha$는 isomorphism이다.
증명
$\alpha$가 잘 정의된다는 것은 자명하다. 이제 $E$가 flat $A$-module이고 $M=A$라 하자. 그럼 주어진
\[\alpha: E\otimes_A\Hom_A(A, N) \rightarrow\Hom_E(E\otimes_AM, E\otimes_AN)\]은 사실 다음의 commutative diagram
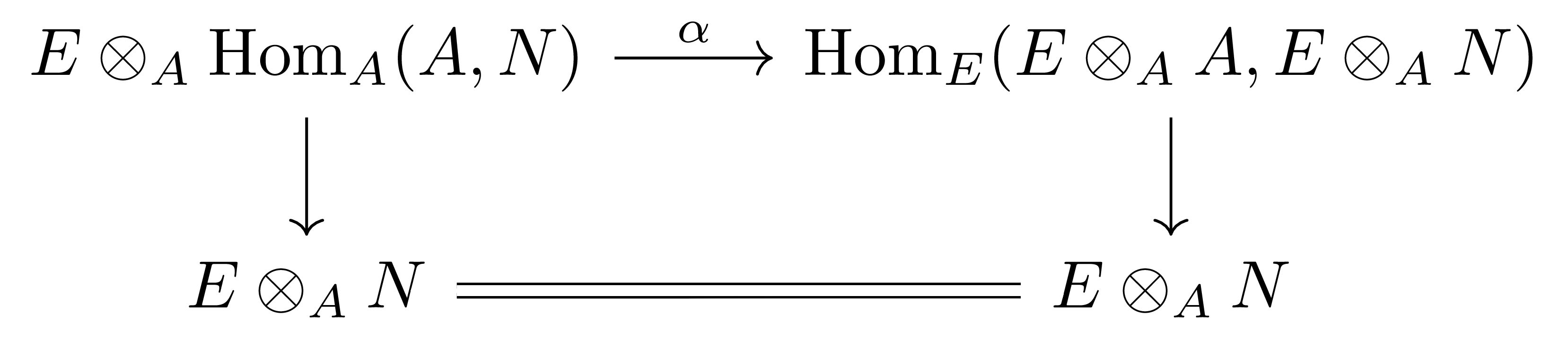
에 넣을 수 있으므로 주어진 명제가 성립한다. 여기서 수직 방향 함수는 각각 isomorphism
\[\Hom_A(A,N)\cong N,\qquad \Hom_E(E\otimes_A,E\otimes_AN)\cong\Hom_E(E,E\otimes_AN)\cong E\otimes_AN\]에서 온 것들이다. 그 후, $\Hom$과 $\otimes$는 유한한 direct sum과 commute하므로 이 명제는 flat $A$-module $E$와 임의의 finitely generated free $A$-module $M$에 대해서도 성립하며, 마지막으로 $M$이 finitely presented인 경우는 다음의 free presentation
\[F \rightarrow G \rightarrow M \rightarrow 0\]을 잡은 후, 다음의 commutative diagram
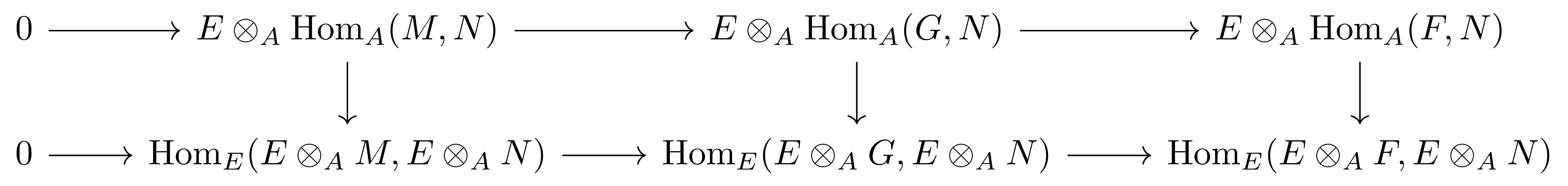
에 four lemma를 사용하면 충분하다.
특별히 다음의 short exact sequence
\[0 \rightarrow M \rightarrow L \rightarrow N \rightarrow 0\]이 주어졌다 하자. 그럼 이 exact sequence가 splitting exact sequence인 것은 임의의 $A$-module $K$에 대하여
\[0 \rightarrow \Hom_\rMod{A}(K,M) \rightarrow \Hom_\rMod{A}(K,L)\rightarrow \Hom_\rMod{A}(K,N) \rightarrow 0\]이 splitting exact sequence인 것과 동치이며, [다중선형대수학] §Hom과 텐서곱, ⁋명제 1의 증명을 보면 실은 $K=N$일 때 위의 sequence가 exact이기만 하면, 즉
\[\Hom_\rMod{A}(N,L) \rightarrow \Hom_\rMod{A}(N,N) \rightarrow 0\]이 surjective이기만 하면 원래의 exact sequence $0 \rightarrow M \rightarrow L \rightarrow N \rightarrow 0$이 splitting exact sequence임을 안다. 따라서 다음을 얻는다.
따름정리 6 임의의 short exact sequence
\[0 \rightarrow M \rightarrow L \rightarrow N \rightarrow 0\]가 주어졌다 하자. 만일 $N$이 finitely presented이고, 모든 maximal ideal $\mathfrak{m}$에 대하여
\[0 \rightarrow M_\mathfrak{m} \rightarrow L_\mathfrak{m} \rightarrow N_\mathfrak{m} \rightarrow 0\]이 splitting exact sequence라면 원래의 exact sequence가 split한다.
아이디얼의 근기
다음의 결과는 엄밀히 이야기하면 localization과는 관계가 없지만, 이를 적어주는 데에 multiplicative subset을 사용하므로 여기에서 언급하고 넘어간다.
명제 7 Ring $A$와 multiplicative subset $S$에 대하여, $\mathfrak{a}$가 $S$와 만나지 않는 ideal 중 maximal한 것이라 가정하자. 그럼 $\mathfrak{a}$는 prime ideal이다.
증명
$A$의 두 원소 $a_1,a_2$가 주어졌다 하고, $a_1,a_2\not\in \mathfrak{a}$라면 $a_1a_2\not\in \mathfrak{a}$임을 보이자. $\mathfrak{a}$의 maximality에 의하여, 두 ideal $\mathfrak{a}+(a_1)$과 $\mathfrak{a}+(a_2)$는 반드시 $S$와 만나야 하므로, 적당한 $b_1,b_2\in A$와 $x_1,x_2\in \mathfrak{a}$에 대하여 $a_ib_i+x_i\in S$가 성립해야 한다. 그런데 $S$는 곱셈에 대해 닫혀있으므로, 다음 원소
\[(a_1b_1+x_1)(a_2b_2+x_2)=a_1a_2b_1b_2+a_1b_1x_2+a_2b_2x_1+x_1x_2\]또한 $S$에 속해있어야 한다. 만일 결론에 반하여 $a_1a_2\in \mathfrak{a}$라면, 우변의 네 항은 모두 $\mathfrak{a}$에 속하므로 이는 $\mathfrak{a}$와 $S$가 만나지 않는다는 가정에 모순이다.
비슷한 맥락에서 다음을 얻는다.
따름정리 8 Ring $A$의 ideal $\mathfrak{a}$에 대하여, $\mathfrak{a}$의 radical근기 $\sqrt{\mathfrak{a}}$를 다음 식
\[\sqrt{\mathfrak{a}}=\{a\mid a^k\in \mathfrak{a}\text{ for some $k\in \mathbb{N}$}\}\]으로 정의하자. 그럼
\[\sqrt{\mathfrak{a}}=\bigcap_\text{\scriptsize$\mathfrak{p}$ prime containing $\mathfrak{a}$} \mathfrak{p}\]이 성립한다.
증명
한쪽 방향은 자명하며, 반대로 만일 $a\not\in \sqrt{\mathfrak{a}}$라면 $S=\{a^k\mid k\geq 1\}$로 두고 §국소화, ⁋명제 10를 적용하면 된다.
참고문헌
[Eis] David Eisenbud. Commutative Algebra: with a view toward algebraic geometry. Springer, 1995.

댓글남기기