이번 글에서 $A$는 noetherian이고 $M$이 finitely generated $A$-module임을 가정한다.
으뜸부분가군
정의 1 $M$의 submodule $N$이 primary submodule으뜸부분가군인 것은 $\Ass(M/N)$이 하나의 prime ideal로만 구성된 것이다. 이 때, $\Ass(M/N)=\{\mathfrak{p}\}$라면 $N$을 $\mathfrak{p}$-primary submodule이라 부른다. 만일 $\Ass(M)$이 하나의 prime ideal로만 이루어져 있다면 $M$을 coprimary submodule쌍대으뜸부분가군이라 부른다.
즉, $M/N$이 coprimary submodule이라면 $N$은 primary submodule이 된다. 또, §동반소아이디얼, ⁋보조정리 5로부터 임의의 $\mathfrak{p}$-primary submodule들의 유한한 교집합은 $\mathfrak{p}$-primary인 것을 안다.
이제 다음이 성립한다.
명제 2 Ring $A$와 prime ideal $\mathfrak{p}$에 대하여 다음이 모두 동치이다.
- $A$-module $M$이 $\mathfrak{p}$-coprimary module이다.
- $\mathfrak{p}$는 $\ann(M)$을 포함하는 prime ideal들 중에서 minimal이며, $\mathfrak{p}$에 속하지 않는 원소들은 $M$의 zero divisor가 아니다.
- 적당한 $k$에 대하여 $\mathfrak{p}^k$가 $M$을 annihilate하며, $\mathfrak{p}$에 속하지 않는 원소들은 $M$의 zero divisor가 아니다.
증명
우선 첫 번째 조건이 성립한다 하면, 정의에 의하여 $\mathfrak{p}$가 $M$의 유일한 associated prime ideal이다. 이제 §동반소아이디얼, ⁋정리 7의 1번 조건에 의하여 $\mathfrak{p}$는 반드시 $\ann(M)$을 포함하는 prime ideal 중 minimal한 것이어야 하며, 2번 조건에 의하여 $\mathfrak{p}$ 바깥에 있는 원소들은 $M$의 zero divisor가 아니다.
이제 두 번째 조건이 성립한다 가정하자. 그럼 $A\setminus \mathfrak{p}$의 원소들은 $M$의 zero divisor가 아니므로, localization $M_\mathfrak{p}$에서 주어진 주장을 증명하면 충분하다. 즉 $(A, \mathfrak{p})$가 local ring이라 가정할 수 있고, 이제 $\mathfrak{p}$가 $\ann(M)$에 대해 minimal하다는 가정과 §국소화의 성질들, ⁋따름정리 8로부터 원하는 결과를 얻는다.
마지막으로 세 번째 조건이 성립한다 하면 $\mathfrak{p}$가 $\ann M$을 포함하는 prime ideal들 가운데 minimal하다는 것은 자명하며, 따라서 §동반소아이디얼, ⁋정리 7의 첫째 조건에 의하여 $\mathfrak{p}$는 $M$의 associated prime ideal이다. 또, $\mathfrak{p}$ 바깥에 있는 원소들은 모두 zero divisor가 아니므로, 다시 §동반소아이디얼, ⁋정리 7의 둘때 조건에 의하여 임의의 associated prime은 항상 $\mathfrak{p}$ 안에 속한다는 것을 안다. 즉, $\mathfrak{p}$가 $M$의 유일한 associated prime ideal이다.
으뜸분해
이번 글에서 우리의 목표는 다음 정리를 보이는 것이다.
정리 3 (Primary decomposition) $M$의 임의의 submodule $M’$은 primary submodule들의 교집합이다. 즉, prime ideal들 $\mathfrak{p}_1,\ldots, \mathfrak{p}_n$과 $\mathfrak{p}_k$-primary submodule들 $M_k$에 대하여, $M’=\bigcap_{k=1}^n M_k$으로 적을 수 있다. 이를 primary decomposition으뜸분해이라 부르며, 그럼 다음이 성립한다.
- $M/M’$의 associated prime은 $\mathfrak{p}_k$들 중 하나이다.
- 만일 $M’$을 표현할 때, $M_k$들 중 불필요한 것이 없다면 $\mathfrak{p}_i$들은 정확히 $M/M’$의 associated prime이다.
- 만일 $M’$을 표현하는 방식 중 더 적은 $M_k$들을 이용하는 방식이 없다면, $M/M’$의 associated prime들은 정확히 index 하나 당 하나의 $\mathfrak{p}_k$가 된다. 만일 여기에 더해 $\mathfrak{p}_i$가 $M/M’$의 annihilator ideal을 포함하는 prime ideal 중 minimal한 것이라면 $M_i$는 $M’$의 $\mathfrak{p}_i$-primary component가 된다.
-
주어진 minimal primary decomposition에 대하여, $A$의 임의의 multiplicative subset $S$에 대해, $\mathfrak{p}_1,\ldots, \mathfrak{p}_m$들이 $S$와 만나지 않는 prim ideal들이라 하자. 그럼
\[S^{-1}M'=\bigcap_{i=1}^m S^{-1}M_i\]은 $S^{-1}A$에 대한 $S^{-1}M$의 minimal primary decomposition이다.
이를 증명하기 위해, 우선 우리는 module의 irreducible decomposition을 정의한다.
정의 4 $A$-module $M$의 임의의 submodule $N$이 irreducible기약이라는 것은 $N=N_1\cap N_2$이도록 하는 $N_1,N_2\supsetneq N$이 존재하지 않는 것이다.
그럼 다음이 성립한다.
보조정리 5 (Noether) $M$의 임의의 submodule은 irreducible submodule들의 교집합으로 나타난다.
증명
귀류법을 사용하자. 그럼 $M$이 noetherian이므로, irreducible submodule들의 교집합으로 나타나지 않는 submodule들 중 maximal한 것을 택할 수 있다. 이를 $N$이라 하자. 그럼 $N$은 irreducible submodule이 아니므로, $N=N_1\cap N_2$이도록 하는 $N_1,N_2\supsetneq N$이 존재한다. 그런데 $N$의 maximality에 의하여 $N_1,N_2$는 모두 irreducible submodule의 교집합으로 나타나고, 따라서 $N$도 그러하므로 모순이다.
이로부터 우리는 $M$의 임의의 submodule $M’$에 대하여, $M’$의 irreducible decomposition기약분해
\[M'=\bigcap_{k=1}^n M_k,\qquad \text{$M_k$ irreducible}\]이 항상 존재한다는 것을 안다.
보조정리 6 위의 irreducible decomposition은 primary decomposition이다.
증명
이를 위해서는 임의의 irreducible submodule $P$이 primary submodule임을 보이면 충분하고, 이는 $M/P$가 coprimary submodule인 것을 보이는 것과 같다. 결론에 반하여 $M/P$가 두 개의 associated prime $\mathfrak{p},\mathfrak{q}$를 갖는다 가정하자. 그럼 $M/P$는 $A/\mathfrak{p}$, $A/\mathfrak{q}$와 각각 isomorphic한 submodule들을 갖는다. 그럼 정의에 의해 $A/\mathfrak{p}$의 $0$이 아닌 임의의 원소의 annihilator는 $\mathfrak{p}$이고, $A/\mathfrak{q}$의 $0$이 아닌 임의의 원소의 annihilator는 $\mathfrak{q}$이므로 이들은 오직 $0$만을 공통의 원소로 갖는다. 즉, $M/P$의 zero submodule $0$은 reducible submodule이다. 이로부터 $M$에서는 $P$이 reducible submodule이 되어 모순이 얻어진다.
따라서 $M$의 임의의 submodule은 항상 primary decomposition을 갖는다. 이제 정리 3의 나머지 부분을 증명해야 한다. 앞선 보조정리의 증명과 마찬가지로, 이들을 증명할 때는 $M/M’$에 대해 증명하면 충분하므로, 일반성을 잃지 않고 $M’=0$으로 가정해도 충분하다.
정리 3의 증명
우선 첫째 결과를 보이기 위해, $M$의 zero submodule $0$의 primary decomposition
\[0=\bigcap_{k=1}^n M_k\]이 주어졌다 하자. 그럼 [다중선형대수학] §완전열, ⁋명제 7의 exact sequence를 일반화한 것으로부터
\[M\subseteq \bigoplus_{k=1}^n M/M_k\]이므로, §동반소아이디얼, ⁋보조정리 5로부터 $\Ass M$의 임의의 prime들이 $\mathfrak{p}_k$들 가운데에서 얻어지는 것을 안다.
이제 둘째 결과를 보이자. 그럼 특히 각각의 $j$에 대하여,
\[\bigcap_{k\neq j} M_k\neq 0\]이 성립한다. 그럼 $M_j\cap \bigcap_{k\neq j}M_k=0$이므로,
\[\bigcap_{k\neq j} M_k=\left(\bigcap_{k\neq j} M_k\right)\bigg/\left(M_k\cap \bigcap_{k\neq j}M_k\right)\cong \left(\bigcap_{k\neq j} M_k + M_j\right)\bigg/M_j\subseteq M/M_j\]가 되어 $\bigcap_{k\neq j} M_k$는 $\mathfrak{p}_j$-coprimary이다. 이로부터 원하는 결과를 얻는다.
이제 세 번째 결과를 보이자. 일반적으로 $\mathfrak{p}$-primary submodule들의 교집합 또한 $\mathfrak{p}$-primary이므로, 주어진 조건을 만족하기 위해서는 $\mathfrak{p}_k$들이 모두 다른 prime ideal들이어야 한다. 이제 $\mathfrak{p}_k$들이 annihilator ideal을 포함하는 것 중 minimal한 것이라 가정하고, $\Ass(M/M_k)=\{\mathfrak{p}_k\}$임을 보이자. 이를 위해서는 $0$이 아닌 임의의 $x+M_k\in M/M_k$에 대하여 $\ann(x)=\mathfrak{p}_k$가 성립해야 하는 것을 보여야 하므로, §국소화, ⁋명제 5에 의하여 이는 $\varepsilon: M \rightarrow M_{\mathfrak{p}_k}$의 kernel이 $M_k$임을 보이면 충분하다.
이제 다음의 commutative diagram
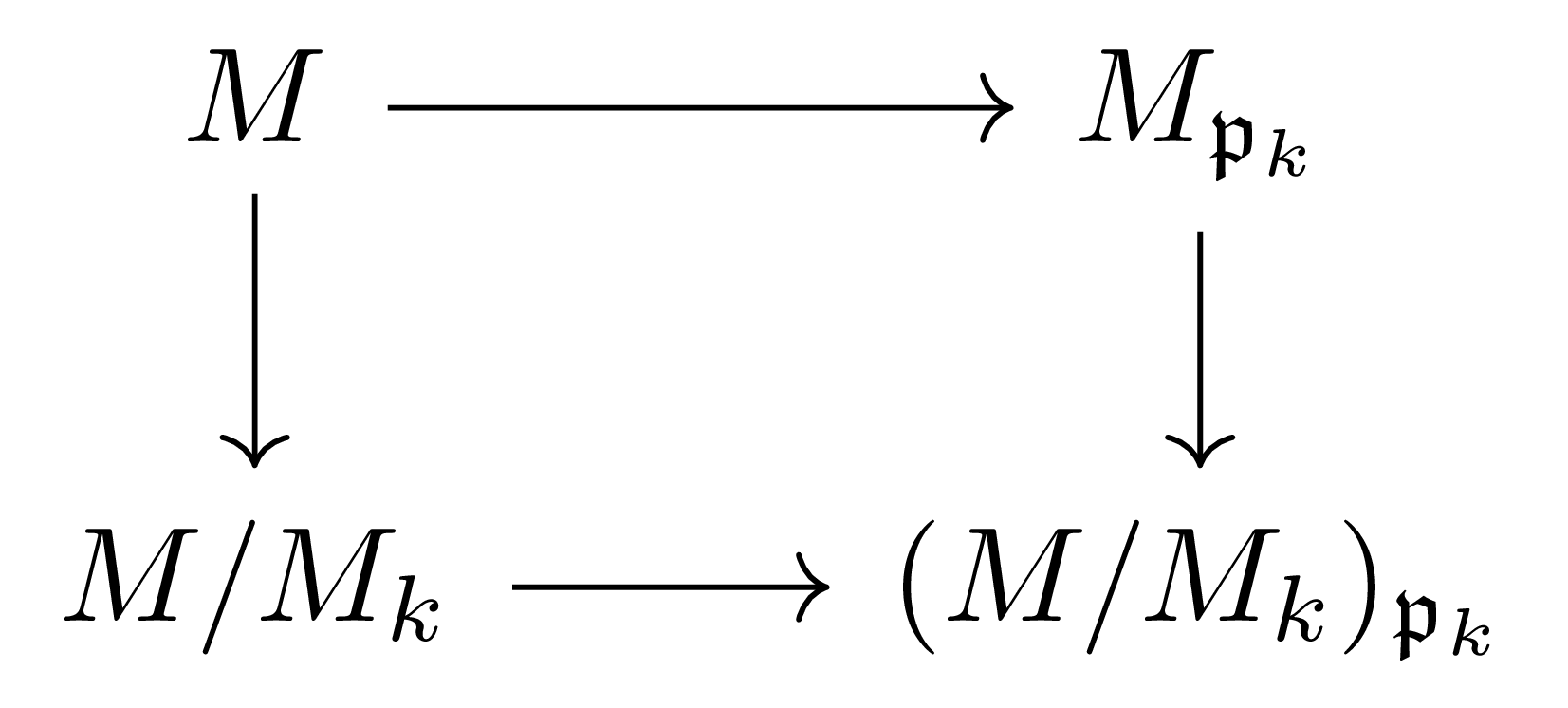
을 생각하자. 그럼 $M \rightarrow M/M_k$의 kernel이 $M_k$이므로, 원하는 주장을 보이기 위해서는 $M_{\mathfrak{p}_k}\rightarrow (M/M_k)_{\mathfrak{p}_k}$ 그리고 $M/M_k \rightarrow (M/M_k)_{\mathfrak{p}_k}$가 모두 injective임을 보이면 충분하다. 우선 $M/M_k \rightarrow (M/M_k)_{\mathfrak{p}_k}$이 injective인 것은 $M_k$가 $\mathfrak{p}_k$-primary라는 것으로부터 자명하다. 그럼 맨 처음 살펴본 것과 같이
\[M \rightarrow \bigoplus_{k=1}^n M/M_k\]이 injective이며, 따라서 이 함수의 localization
\[M_{\mathfrak{p}_k} \rightarrow \left(\bigoplus_{k=1}^n M/M_k\right)_{\mathfrak{p}_k}\]또한 injective이다. 한편, 각각의 $j\neq k$에 대하여 $M/M_j$는 $\mathfrak{p}_j$-coprimary이고, minimality로부터 $\mathfrak{p}_j$는 $\mathfrak{p}_i$에 속하지 않아야 하므로 $(M/M_j)_{\mathfrak{p}_k}=0$이 성립하게 되고, 이렇게 얻어지는 함수가 정확히 $M_{\mathfrak{p}_k}\rightarrow (M/M_k)_{\mathfrak{p}_k}$이므로 원하는 결과를 얻는다.
마지막 주장은 거의 자명하다.
으뜸분해와 인수분해
한편, 다음 정리는 primary decomposition이 우리가 알고 있던 인수분해의 개념을 일반화한 것임을 보여준다.
정리 7 Noetherian domain $A$에 대해 다음이 성립한다.
- $f\in A$가 다음 식 $f=u p_1^{e_1}\cdots p_n^{e_n}$으로 인수분해된다 하자. 여기서 $u$는 unit이고 $p_i$는 $(p_i)$들이 서로 다른 prime ideal이도록 하는 원소들이다. 그럼 $(f)=\bigcap(p_i^{e_i})$가 $(f)$의 minimal primary decomposition이다.
- $A$가 UFD인 것과, principal ideal에 대한 minimal prime ideal들이 모두 principal인 것이 동치이다.
증명
참고문헌
[Eis] David Eisenbud. Commutative Algebra: with a view toward algebraic geometry. Springer, 1995.

댓글남기기