앞선 글에서 우리는 \(A\)-module \(M\)이 언제 flat인지를 판단하는 몇 가지 기준들을 살펴보았는데, 이번 글에서는 특별히 localization을 통해 이를 판단하는 기준을 살펴본다. 다음 정리는 §평탄성, ⁋명제 1을 maximal ideal에 대해서만 확인해도 충분하다는 것을 보여준다.
정리 1 Noetherian local ring \((A, \mathfrak{m})\)을 고정하고, \((E, \mathfrak{n})\)가 \(\mathfrak{m}E\subseteq \mathfrak{n}\)를 만족하는 local Noetherian \(A\)-algebra라 가정하자. 그럼 finitely generated \(E\)-module \(M\)에 대하여, \(M\)이 flat \(A\)-module인 것과 \(\Tor_1^A(A/\mathfrak{m}, M)=0\)인 것이 동치이다.
증명
만일 \(M\)이 flat \(A\)-module이라면 \(\Tor_1^A(A/\mathfrak{m}, M)=0\)인 것은 정확히 §평탄성, ⁋명제 1의 내용이므로, 반대 방향만 보이면 충분하다.
반대방향을 보이기 위해서도 마찬가지로 §평탄성, ⁋명제 1를 사용하여, 주어진 조건을 가정한 후 임의의 \(A\)의 ideal \(\mathfrak{a}\)에 대하여 multiplication map \(m:\mathfrak{a}\otimes_AM \rightarrow M\)이 injective인 것을 보이면 충분하다. 이를 위해 \(x\in \mathfrak{a}\otimes_AM\)이 multiplication map의 kernel \(\ker m\)에 속한다 가정하고, \(x=0\)임을 보이자. 우선 \(M\) 위에 정의된 \(E\)-module structure로부터 \(\mathfrak{a}\otimes_AM\) 위에도 자연스럽게 \(E\)-module 구조가 있으며, 가정 \(\mathfrak{m}E\subseteq \mathfrak{n}\)으로부터, 임의의 \(n\)에 대해 다음의 식
\[\mathfrak{m}^n(\mathfrak{a}\otimes_AM )\subseteq \mathfrak{n}^n(\mathfrak{a}\otimes_AM)\]이 성립하는 것을 안다. 한편, 이들은 finitely generated \(E\)-module이므로 §부풀림 대수, ⁋따름정리 8로부터
\[\bigcap \mathfrak{m}^n(\mathfrak{a}\otimes_AM)=\bigcap \mathfrak{n}^n(\mathfrak{a}\otimes_AM)=0\]이다. 따라서, \(x=0\)인 것을 보이는 것은 모든 \(n\)에 대하여 \(x\in \mathfrak{m}^n(\mathfrak{a}\otimes_AM)\)이 성립하는 것을 보이면 충분하다. 한편, \(\mathfrak{m}^n(\mathfrak{a}\otimes_AM)\)은 \((\mathfrak{m}^n \mathfrak{a})\otimes_AM\)과 identify할 수 있고, §부풀림 대수, ⁋보조정리 7를 다음의 \(\mathfrak{m}\)-stable filtration
\[\mathfrak{m}\supseteq \mathfrak{m}^2\supseteq\cdots\]과 \(M'=\mathfrak{a}\)에 적용하면, 다음의 filtration
\[\mathfrak{m}\cap \mathfrak{a}\supseteq \mathfrak{m}^2 \cap\mathfrak{a}\supseteq\cdots\]또한 \(\mathfrak{m}\)-stable이므로, 적당한 \(N\)이 존재하여 \(m>N\)일 때마다 모든 \(i\)에 대해
\[\mathfrak{m}^{m+i}\cap \mathfrak{a}=\mathfrak{m}^i(\mathfrak{m}^m\cap \mathfrak{a})\]가 성립하도록 할 수 있다. 따라서 임의의 \(n\)이 주어질 때마다, \(t>N+n\)이도록 잡으면
\[\mathfrak{m}^t\cap \mathfrak{a}=\mathfrak{m}^n(\mathfrak{m}^{t-n}\cap \mathfrak{a})\subseteq \mathfrak{m}^n \mathfrak{a}\]이 되고, 우리는 \(x\in (\mathfrak{m}^na)\otimes_AM\)가 임의의 \(n\)에 성립하는 것을 보이는 대신, 임의의 \(t\)에 대해 \(x\in (\mathfrak{m}^t\cap \mathfrak{a})\otimes_AM\)가 성립하는 것을 보여도 된다.
이제 다음의 short exact sequence
\[0 \rightarrow \mathfrak{m}^t\cap \mathfrak{a} \rightarrow \mathfrak{a} \rightarrow \frac{\mathfrak{a}}{\mathfrak{m}^t\cap \mathfrak{a}} \rightarrow 0\]에 \(-\otimes_AM\)을 취하면 다음의 exact sequence
\[(\mathfrak{m}^t\cap \mathfrak{a})\otimes_AM \rightarrow \mathfrak{a}\otimes_AM \rightarrow \frac{\mathfrak{a}}{\mathfrak{m}^t\cap \mathfrak{a}}\otimes_AM \rightarrow 0\]를 얻으며, 이 상황에서 \(x\)는 \((\mathfrak{a}/\mathfrak{m}^t\cap \mathfrak{a})\otimes_AM\)으로 옮겨졌을 때 \(0\)이 된다는 것을 보이면 충분하다. 한편, 다음의 commutative diagram
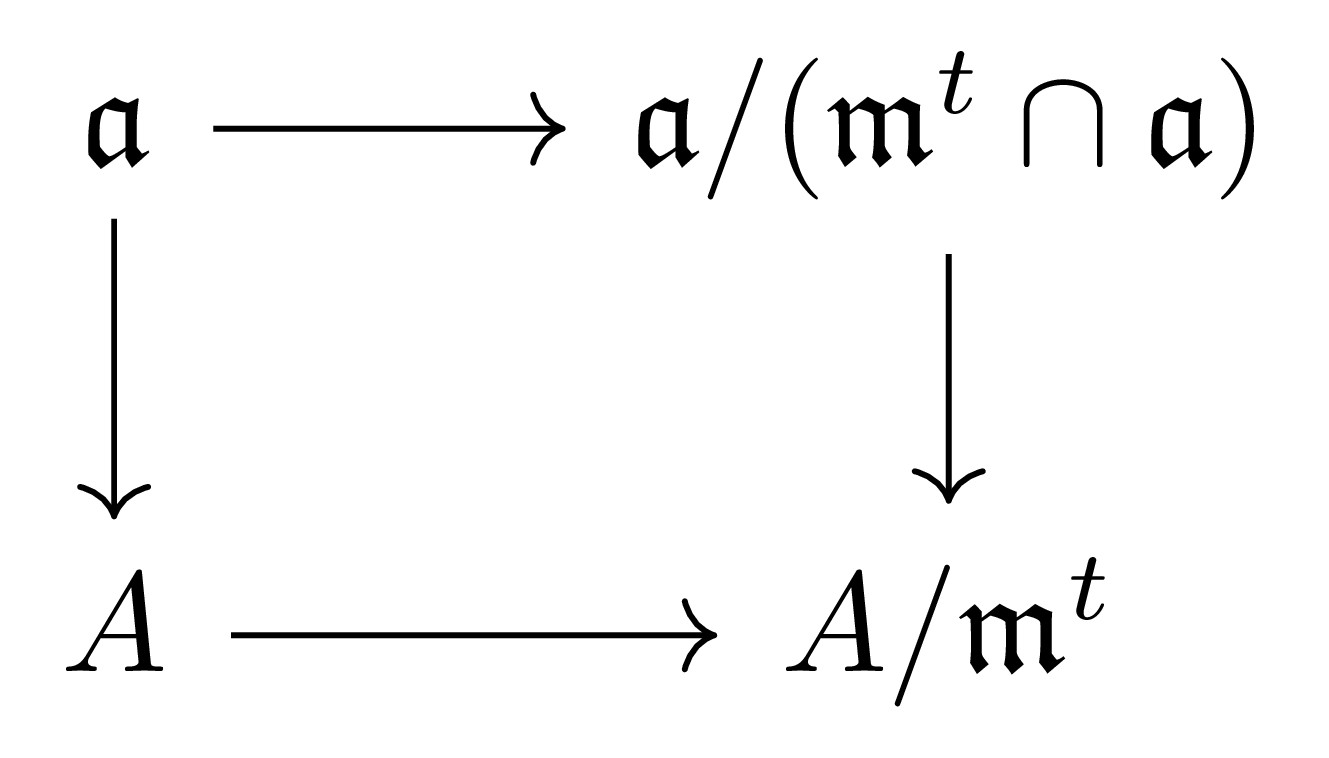
에 \(-\otimes_AM\)을 취해 얻어지는 다음의 commutative diagram
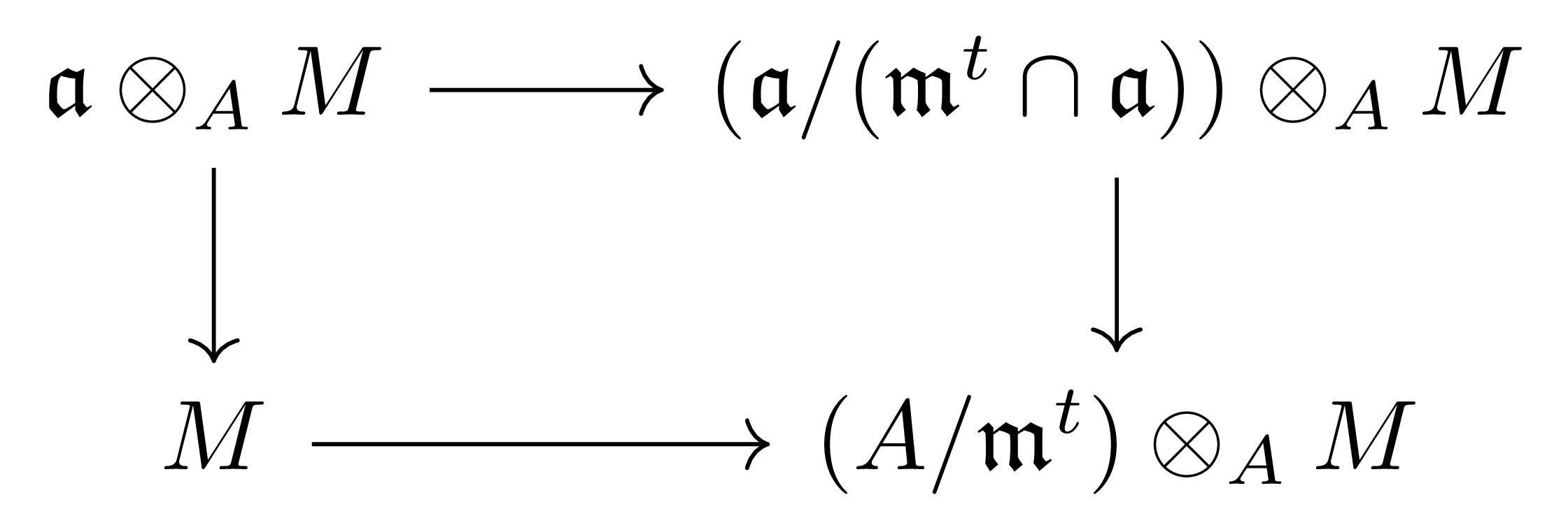
을 생각하면, 왼쪽 \(\mathfrak{a}\otimes_AM \rightarrow M\)은 multiplication map \(m\)이고, 따라서 \(x\in\ker m\)는 \(\llcorner\) 방향으로의 합성을 통해 \(0\)으로 옮겨진다. 따라서 오른쪽 \((\mathfrak{a}/(\mathfrak{m}^t\cap I))\otimes_AM \rightarrow (A/\mathfrak{m}^t)\otimes_AM\)이 injective인 것만 보이면 충분하다. 다음의 isomorphism
\[\frac{\mathfrak{a}}{\mathfrak{m}^t\cap \mathfrak{a}}\cong \frac{\mathfrak{a}+\mathfrak{m}^t}{\mathfrak{m}^t}\]을 통하면, 이 함수를 주는 \(\mathfrak{a}/(\mathfrak{m}^t\cap \mathfrak{a}) \rightarrow A/\mathfrak{m}^t\)는 정확히 다음의 short exact sequence
\[0 \rightarrow \frac{\mathfrak{a}+\mathfrak{m}^t}{\mathfrak{m}^t} \rightarrow \frac{A}{\mathfrak{m}^t}\rightarrow \frac{A}{\mathfrak{a}+\mathfrak{m}^t} \rightarrow 0\]의 왼쪽 함수와 같다. 따라서, \(\Tor\) long exact sequence
\[\cdots \Tor_1^A(A/(\mathfrak{a}+\mathfrak{m}^t), M) \rightarrow \frac{\mathfrak{a}+\mathfrak{m}^t}{\mathfrak{m}^t}\otimes_AM \rightarrow \frac{A}{\mathfrak{m}^t}\otimes_AM \rightarrow\]로부터, 우리가 보여야 할 것은 \(\Tor_1^A(A/(\mathfrak{a}+\mathfrak{m}^t), M)=0\)이다.
그런데 \(A/(\mathfrak{a}+\mathfrak{m}^t)\)는 \(\mathfrak{m}^t\)로 annihilate되고, \(\mathfrak{m}^t\)는 finitely generated이므로, 이를 통해 \(A/(\mathfrak{a}+\mathfrak{m}^t)\)이 finite length를 갖는다는 것을 안다. 따라서, 더 일반적으로 유한한 길이를 갖는 임의의 \(A\)-module \(N\)이 주어질 때마다 \(\Tor_1^A(N, M)=0\)이 성립한다는 것을 보이면 원하는 바를 얻는다.
귀납법으로 진행한다. 만일 \(N\)이 length \(1\)이라면 §조르단-횔더 정리, ⁋정의 1 이후의 논중으로부터 \(N=A/\mathfrak{m}\)이어야 하고, 따라서 \(\Tor_1^A(N, M)=0\)인 것은 정확히 정리의 가정과 일치한다. 유한한 length의 \(A\)-module \(N\)과, \(N\)의 임의의 proper submodule \(N'\)을 택하자. 그럼 다음의 exact sequence
\[0 \rightarrow N' \rightarrow N \rightarrow N/N' \rightarrow 0\]에 \(\Tor\) long exact sequence를 적용하여
\[\cdots \rightarrow\Tor_1^A(N', M) \rightarrow \Tor_1^A(N, M) \rightarrow \Tor_1^A(N/N', M) \rightarrow \cdots\]를 얻는다. 이제 귀납적 가정에 의하여 \(\Tor_1^A(N, M)=\Tor_1^A(N/N',M)=0\)이므로 원하는 결과를 얻는다.
한편, \(M\)이 flat \(A\)-module이라면 임의의 \(A/(a)\)-module \(N\)에 대하여
\[(M/aM)\otimes_{A/(a)}N=(A/(x)\otimes_A M)\otimes_{A/(a)} N\cong M\otimes_AN\]이므로 \(M/aM\)은 아무런 조건 없이도 flat \(A/(a)\)-module이다. 우리는 따름정리 3에서 정리 1의 조건을 가정하고 이 주장의 역을 보인다. 이를 위해서는 우선 다음 보조정리가 필요하다.
보조정리 2 \(A\)-module \(M\)이 주어졌다 하고, \(a\in A\)가 \(A\)와 \(M\) 모두에서 non-zerodivisor라 하자. 그럼 임의의 \(A/(a)\)-module \(N\)에 대하여,
\[\Tor_i^{A/(a)}(N, M/aM)=\Tor_i^A(N,M)\]이 성립한다.
증명
\(A\)-module \(M\)의 free resolution
\[\cdots \rightarrow F_2 \rightarrow F_1 \rightarrow F_0\tag{1}\]을 생각하면, 정의에 의해 다음 chain complex
\[\cdots \rightarrow N\otimes_A F_2 \rightarrow N\otimes_AF_1 \rightarrow N\otimes_A F_0\]의 \(i\)번째 homology가 \(\Tor_i^A(M,N)\)이다. 한편, (1)에 \(A/(a)\otimes_A-\)를 취해 얻어지는 다음의 complex
\[\cdots \rightarrow F_2/aF_2 \rightarrow F_1/aF_1 \rightarrow F_0/aF_0 \rightarrow M/aM \rightarrow 0\tag{2}\]를 생각하자. 그럼 이 complex의 호몰로지는
\[\Tor_i^A(A/(a), M)=\begin{cases} M/aM&\text{if $i=0$}\\ 0&\text{otherwise}\end{cases}\]로 주어지므로, 이는 \(M/aM\)의 free resolution이 된다. 따라서 \(\Tor_i^{A/(a)}(N, M/aM)\)을 예산하기 위해서 (2)를 사용하면 다음의 isomorphism
\[N\otimes_{A/(a)} F_i/aF_i=N\otimes_{A/(a)} ((A/(a))\otimes_A F_i)\cong N\otimes_A F_i\]을 통해 원하는 결과를 얻는다.
이를 사용하여 다음을 보일 수 있다.
따름정리 3 Noetherian local ring \((A, \mathfrak{m})\)을 고정하고, \((E, \mathfrak{n})\)가 \(\mathfrak{m}E\subseteq \mathfrak{n}\)를 만족하는 local Noetherian \(A\)-algebra라 가정하자. 만일 \(a\in \mathfrak{m}\)이 \(A\)의 non-zerodivisor인 동시에 finitely generated \(E\)-module \(M\)의 zerodivisor라면, \(M\)이 flat \(A\)-module인 것과 \(M/aM\)이 flat \(A/(a)\)-module인 것이 동치이다.
증명
\(M/aM\)이 flat \(A/(a)\)-module이라 하자. \(A\)의 residue field를 \(A/\mathfrak{m}\)에 대하여, 가정으로부터
\[\Tor_1^{A/(a)}(A/\mathfrak{m}, M/aM)=0\]이 성립하고, 이제 보조정리 2를 적용하면 \(\Tor_1^A(A/\mathfrak{m}, M)=0\)이 성립하는 것을 안다. 따라서 정리 1에 의하여 \(M\)은 flat \(A\)-module이다.
Rees algebra
정의 4 Ring \(A\)와 ideal \(\mathfrak{a}\)에 대하여, Rees algebra리스 대수는
\[A[\mathfrak{a}t]=\bigoplus_{n=0}^\infty \mathfrak{a}^n t^n\subseteq A[t]\]를 의미한다. 또, 같은 상황에서 extended Rees algebra확장된 리스 대수를
\[A[\mathfrak{a}t, t^{-1}]=\bigoplus_{n=-\infty}^\infty \mathfrak{a}^nt^n\subseteq A[t, t^{-1}]\]로 정의한다.
그럼 다음 따름정리는 거의 자명하다.
명제 5 Field \(\mathbb{K}\)와 \(\mathbb{K}\)-algebra \(A\)를 고정하자. 그럼 Rees algebra \(A[\mathfrak{a}t, t^{-1}]\)은 flat \(\mathbb{K}[t]\)-module이다. 또, 만일 \(\bigcap \mathfrak{a}^i=0\)이라면, \(1-t s\) (\(s\in S\)) 꼴의 원소들은 모두 \(A[\mathfrak{a}t, t^{-1}]\)에서 non-zerodivisor이다.

댓글남기기