분해

사영분해와 단사분해

우리는 [다중선형대수학] §사영가군, 단사가군, 평탄가군, ⁋정의 3에서 사영가군과 단사가군을 정의하였다. 이를 diagram의 언어로 바꾸어 쓰면 일반적인 abelian category에서 projective object와 injective object의 개념을 얻는다.

정의 1 Abelian category \(\mathcal{A}\)를 고정하자.

1. \(\mathcal{A}\)의 대상 \(P\)가 projective object_{사영 대상}라는 것은 다음의 diagram

   

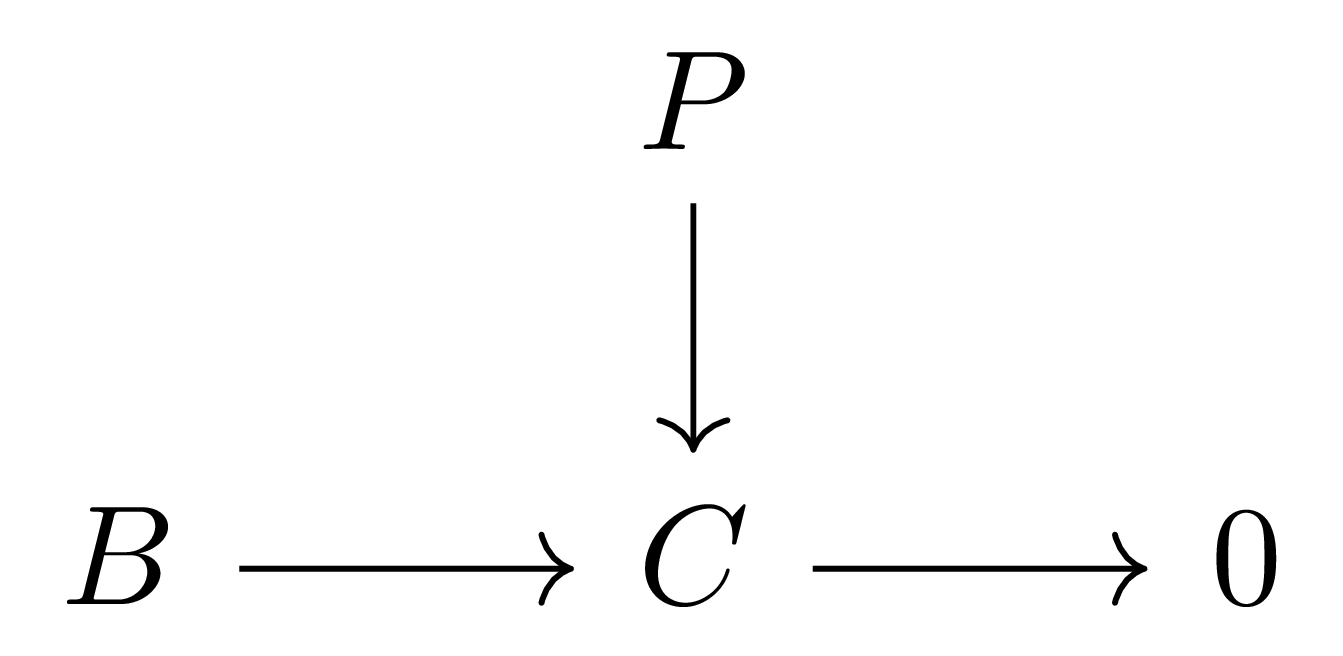
   이 주어질 때마다, 다음 diagram

   

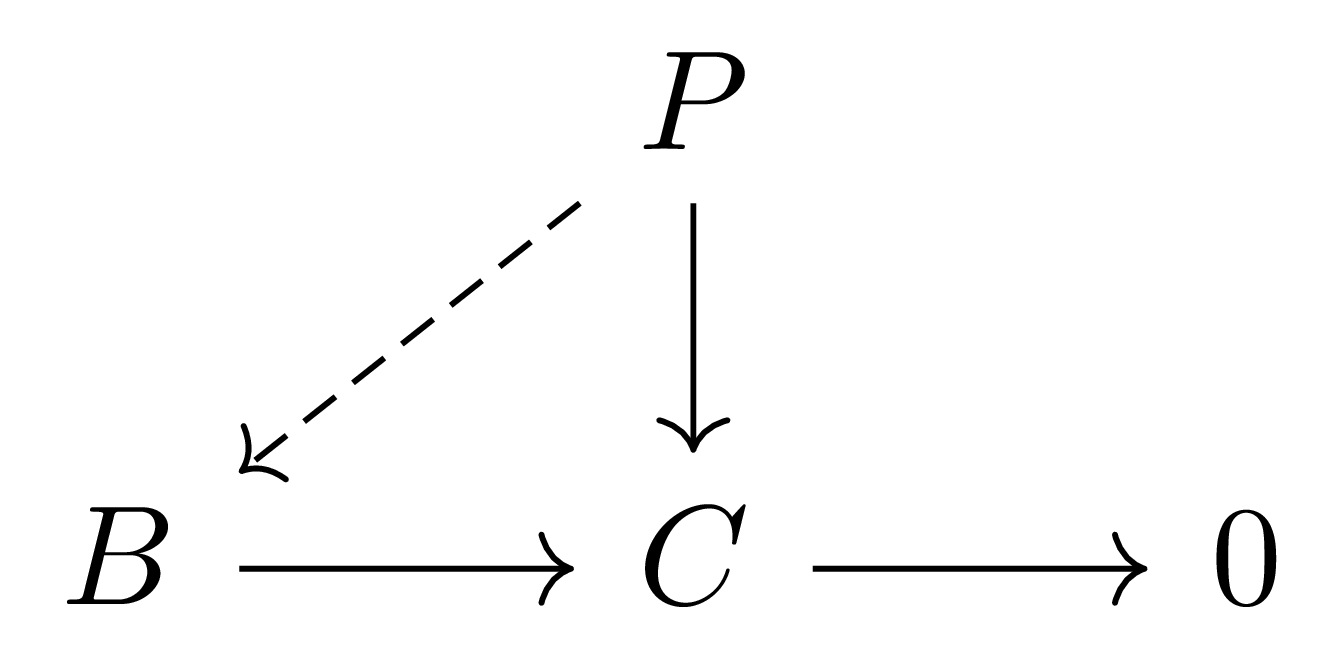
   을 commute하게 하는 \(P \rightarrow B\)가 적어도 하나 존재하는 것이다.
   만일 \(\mathcal{A}\)의 임의의 대상 \(A\)마다 적당한 projective object \(P\)가 존재하여 \(P \rightarrow A \rightarrow 0\)이 exact이도록 할 수 있다면, \(\mathcal{A}\)가 enough projective를 갖는다 말한다.

2. \(\mathcal{A}\)의 대상 \(I\)가 injective object_{단사 대상}라는 것은 다음의 diagram

   

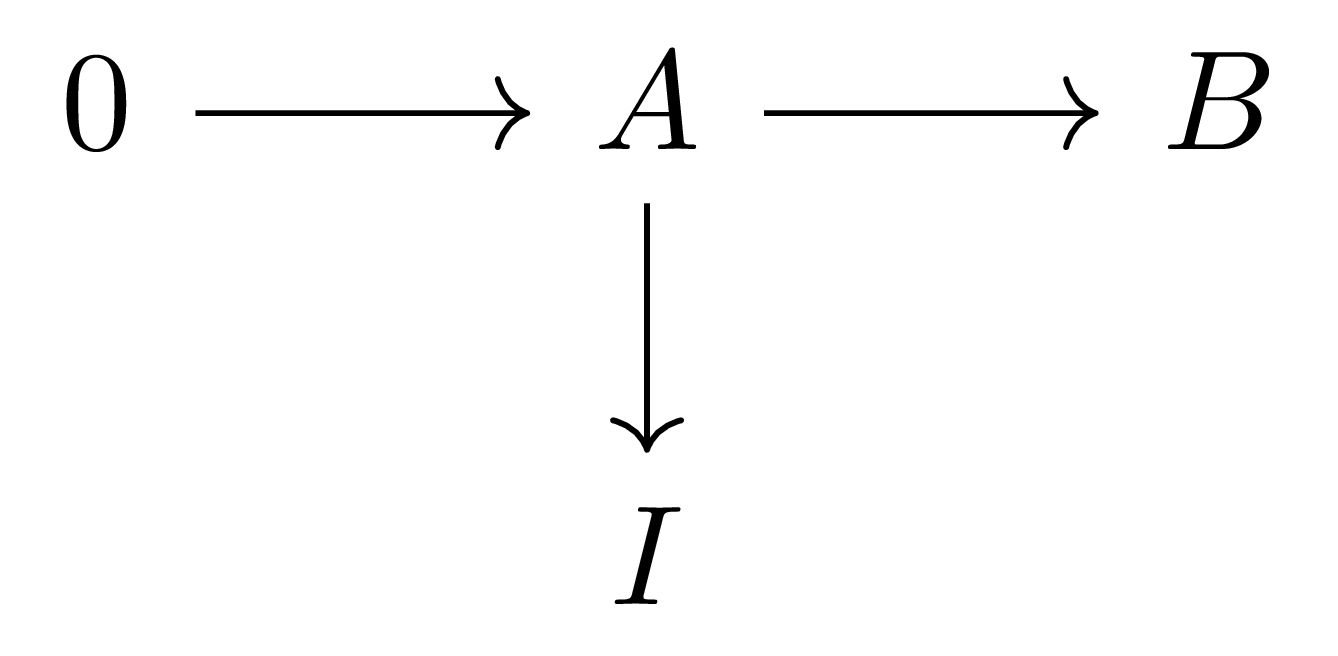
   이 주어질 때마다, 다음 diagram

   

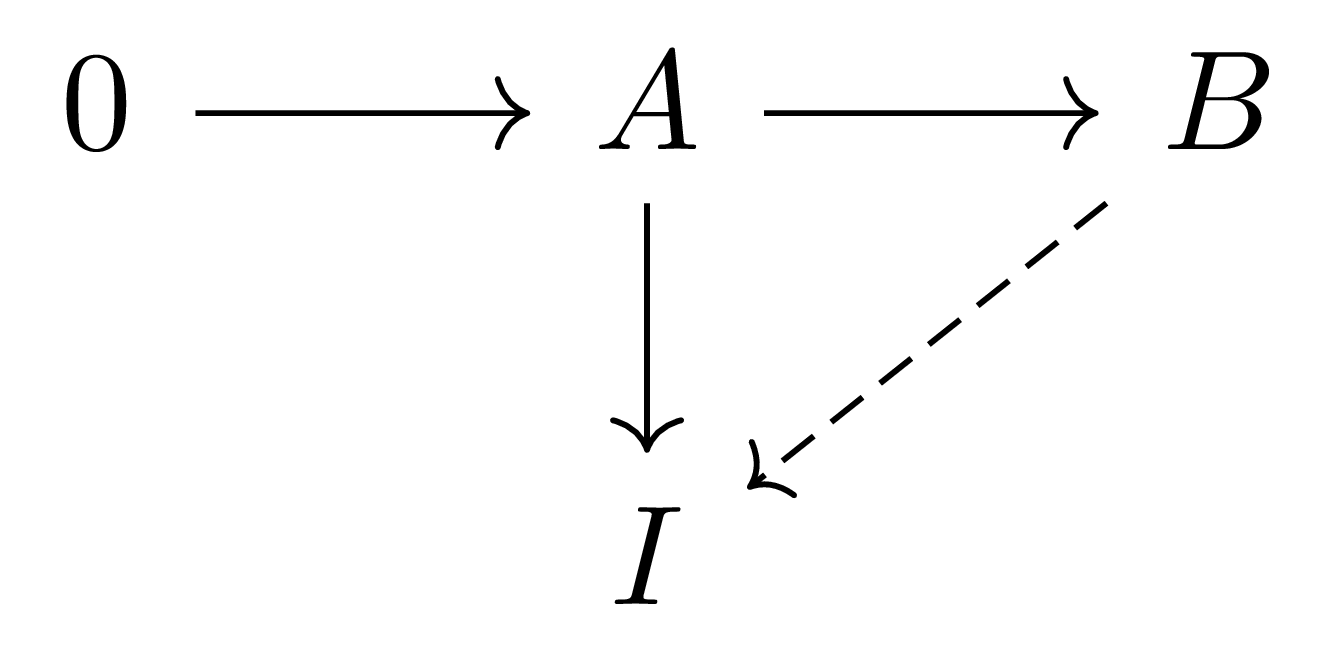
   을 commute하게 하는 \(B \rightarrow I\)가 적어도 하나 존재하는 것이다.
   만일 \(\mathcal{A}\)의 임의의 대상 \(A\)마다 적당한 injective object \(I\)가 존재하여 \(0 \rightarrow A \rightarrow I\)이 exact이도록 할 수 있다면, \(\mathcal{A}\)가 enough injective를 갖는다 말한다.

또, 다음을 정의한다.

정의 2 Abelian category \(\mathcal{A}\)의 대상 \(M\)에 대하여, 다음을 정의한다.

1. \(M\)의 left resolution_{왼쪽 분해}은 다음의 chain complex

   \[\cdots \longrightarrow P_2 \longrightarrow P_1 \longrightarrow P_0 \overset{\epsilon}{\longrightarrow} M \longrightarrow 0\]

   가 exact이도록 하는 chain complex \(P_\bullet\)과 augmentation map \(\epsilon: P_0 \rightarrow M\)이다. 만일 각 \(P_i\)들이 모두 projective object들이라면 이를 projective resolution_사영분해라 부른다.

2. \(M\)의 right resolution_{오른쪽 분해}은 다음의 chain complex

   \[0 \longrightarrow M \overset{\eta}{\longrightarrow} I^0 \longrightarrow I^1 \longrightarrow I^2 \longrightarrow \cdots\]

   가 exact이도록 하는 cochain complex \(I^\bullet\)과 augmentation map \(\eta: M \rightarrow I^0\)이다. 만일 각 \(I^i\)들이 모두 injective object들이라면 이를 injective resolution_단사분해라 부른다.

\(\mathcal{A}\)의 projective object는 \(\mathcal{A}^\op\)의 injective object이다. 마찬가지로 \(\mathcal{A}\)가 enough projective를 갖는다면 \(\mathcal{A}^\op\)는 enough injective를 갖는다. 또, \(M\)의 \(\mathcal{A}\)에서의 projective resolution은 \(M\)의 \(\mathcal{A}^\op\)에서의 injective resolution과 동일하다. 때문에 다음 명제는 projective resolution에 대한 것만 증명해도 충분하다.

명제 3 Abelian category \(\mathcal{A}\)가 enough projective를 갖는다면, \(\mathcal{A}\)의 임의의 대상 \(M\)은 projective resolution을 갖는다. 마찬가지로, abelian category \(\mathcal{A}\)가 enough injective를 갖는다면, \(\mathcal{A}\)의 임의의 대상 \(M\)은 injective resolution을 갖는다.

증명

우선 \(\mathcal{A}\)가 enough projective를 갖는 것으로부터 적당한 surjection \(\epsilon_0:P_0 \rightarrow M\)을 잡을 수 있다. \(M_0=\ker \epsilon_0\)이라 하자. 그럼 \(\mathcal{A}\)는 enough projective를 가지므로, 적당한 surjection \(\epsilon_1:P_1 \rightarrow M_0\)을 잡을 수 있다. 이제 \(\epsilon_1: P_1 \rightarrow M_0\)과 inclusion \(\iota_0: M_0 \rightarrow P_0\)을 합성한 \(d_1=\iota_0\circ\epsilon_1\)까지를 diagram으로 그리면 다음과 같다.

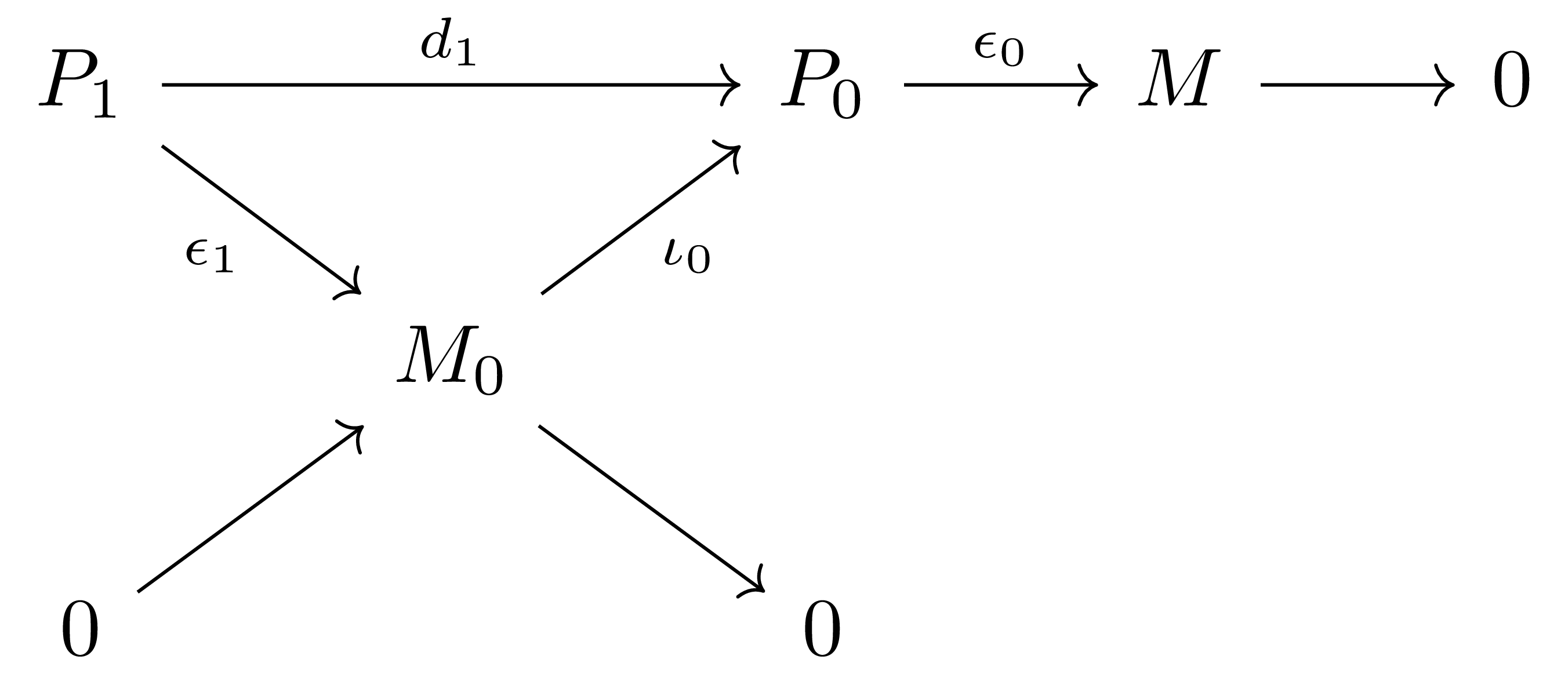
이러한 방식으로, \(\epsilon_n:P_n \rightarrow M_{n-1}\)이 주어질 때마다 \(M_n=\ker \epsilon_n\)으로 잡아 다음과 같은 commutative diagram

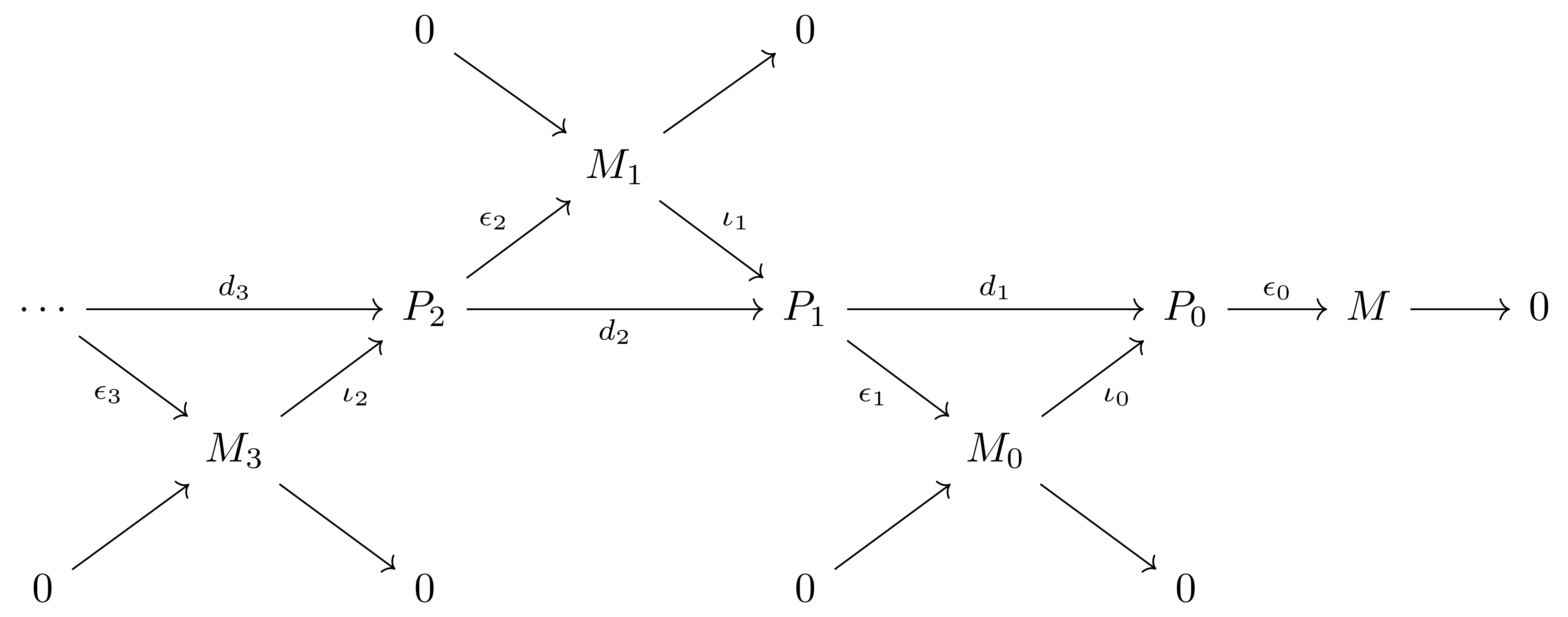
을 얻는다. 그럼 가운데에서 얻어지는

\[\cdots \overset{d_3}{\longrightarrow} P_2 \overset{d_2}{\longrightarrow} P_1 \overset{d_1}{\longrightarrow} P_0 \overset{\epsilon_0}{\longrightarrow} M \longrightarrow 0\]

을 보면, 다음의 식

\[\im(d_n)=\im(\iota_{n-1}\circ\epsilon_n)=\im(\iota_{n-1})=\ker(\epsilon_{n-1})=\ker(\iota_{n-2}\circ\epsilon_{n-1})=\ker(d_{n-1})\]

을 얻는다. 여기서 식 \(\im(\iota_{n-1}\circ\epsilon_n)=\im(\iota_{n-1})\)는 \(\epsilon_n\)이 surjective라는 것을, 식 \(\ker(\epsilon_{n-1})=\ker(d_{n-1})\)은 \(\iota_{n-2}\)이 injective라는 것을 각각 이용하였다. 따라서 \(P_\bullet\)은 \(M\)의 projective resolution이다.

이번 글에서 우리의 목표 중 하나는 임의의 \(A\)-module은 항상 projective resolution과 injective resolution을 갖는다는 것을 증명하는 것이다. 명제 3을 사용하면 이는 \(\lMod{A}\)가 enough projective와 enough injective를 갖는다는 것을 증명하면 충분하다. \(\lMod{A}\)가 enough projective를 갖는다는 것은 자명하다.

명제 4 Category \(\lMod{A}\)는 enough projective를 갖는다.

증명

[다중선형대수학] §기저, ⁋명제 2 그리고 [다중선형대수학] §사영가군, 단사가군, 평탄가군, ⁋명제 4에 의하여 자명하다.

그러나 \(\lMod{A}^\op\)에 대해서는 아는 것이 아무것도 없으므로, \(\lMod{A}\)가 enough injective를 갖는다는 것은 위의 결과로부터 따라나오지 않는다. 따라서 다음의 명제는 별도의 증명이 필요하다.

명제 5 Category \(\lMod{A}\)는 enough injective를 갖는다.

증명

어렵지 않게 right adjoint는 injective object를 보존함을 보일 수 있다. 그럼 ring homomorphism \(\mathbb{Z}\rightarrow A\)로부터 얻어지는 coextension of scalar \(\Ab \rightarrow \lMod{A}\)는 restriction of scalar의 right adjoint이므로 \(\Ab\)의 injective object는 \(\lMod{A}\)로 갔을 때 injective object가 된다. ([대수적 구조] §스칼라의 변환, ⁋명제 6) 따라서 원하는 증명은 \(\Ab\)가 enough injective를 갖는다는 사실을 증명하면 충분하다. 이는 임의의 \(A\in\Ab\)에 대하여,

\[I(A)=\prod_{f\in\Hom_\Ab(A, \mathbb{Q}/\mathbb{Z})} \mathbb{Q}/\mathbb{Z}\]

그리고 \(e_A:A \rightarrow I(A)\)를 \(a\mapsto (f(a))_{f\in\Hom(A, \mathbb{Q}/\mathbb{Z})}\)으로 정의하면 된다.

분해의 유일성

한편, 사영분해와 단사분해의 유일성은 다음의 더 강력한 정리로부터 얻어진다.

정리 6 Projective resolution \(P_\bullet \rightarrow M\)과 임의의 \(u:M \rightarrow N\)이 주어졌다 하자. 그럼 임의의 left resolution \(Q_\bullet \rightarrow N\)가 주어질 때마다 다음의 diagram

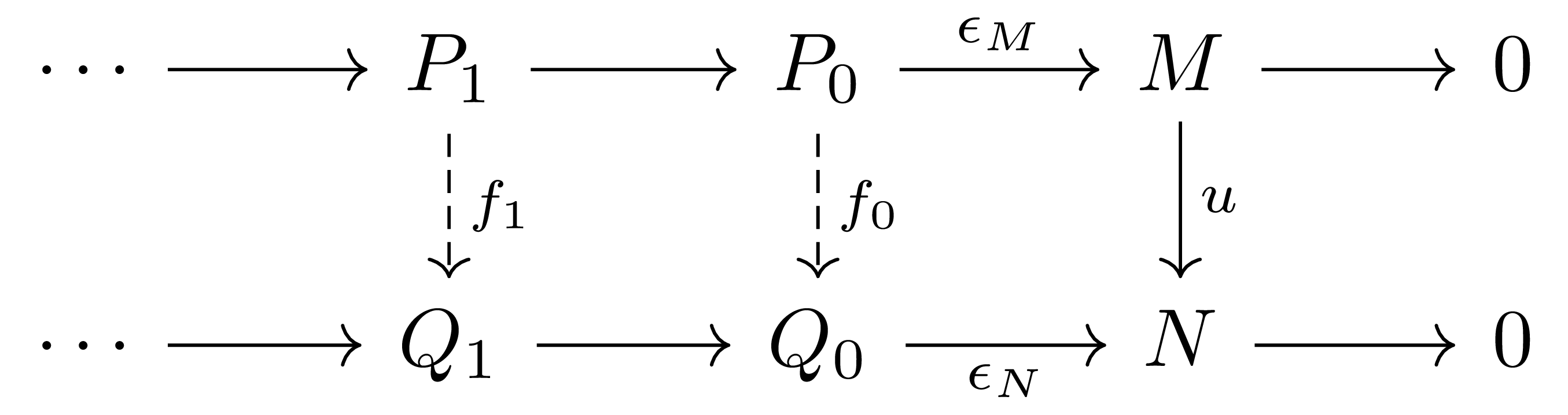
을 commute하게 하는 chain map \(f:P_\bullet \rightarrow Q_\bullet\)이 up to homotopy로 유일하게 존재한다.
비슷하게, injective resolution \(N \rightarrow I^\bullet\)과 임의의 \(u: M \rightarrow N\)이 주어졌다 하자. 그럼 임의의 right resolution \(M \rightarrow J^\bullet\)가 주어질 때마다 다음의 diagram

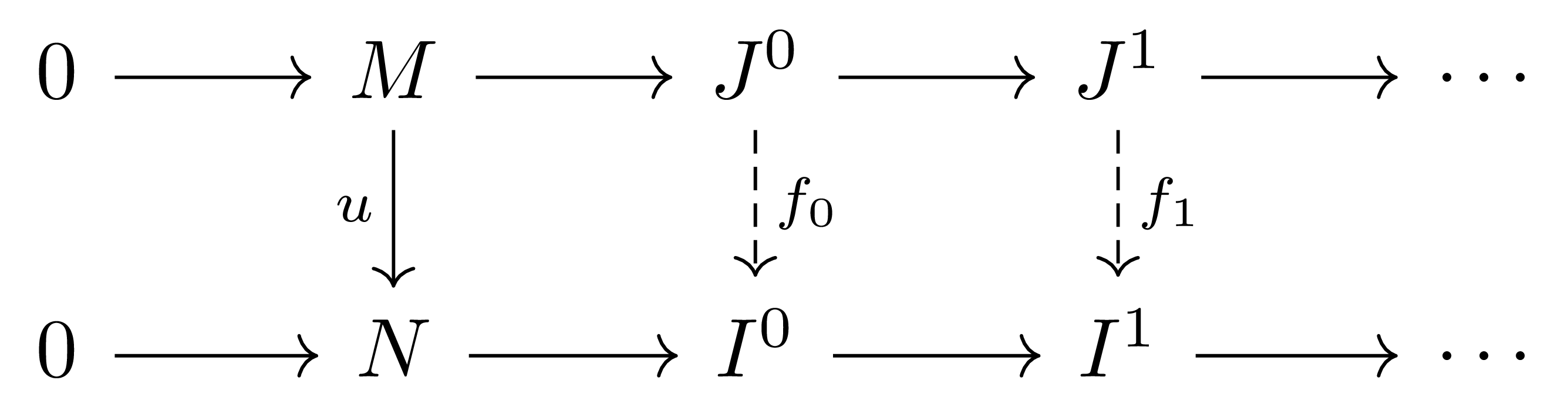
을 commute하게 하는 chain map \(f:J^\bullet \rightarrow I^\bullet\)이 존재한다.

증명

마지막으로, 다음 글에서 중요하게 사용할 다음 보조정리를 증명하고 마친다.

보조정리 7 다음의 short exact sequence

\[0 \longrightarrow A'\overset{i}{\longrightarrow}A\overset{p}{\longrightarrow}A'' \longrightarrow 0\]

가 주어졌다 하고, \(A'\), \(A''\)의 projective resolution들 \(P_\bullet'\), \(P_\bullet''\)이 주어졌다 하자. 그럼 \(P_n=P_n'\oplus P_n''\)으로 정의되는 chain complex \(P_\bullet\)은 \(A\)의 projective resolution이 되며, 이들 complex들 사이의 exact sequence

\[0 \rightarrow P' \rightarrow P \rightarrow P'' \rightarrow 0\]

이 존재한다.

증명

우선 주어진 상황을 diagram으로 그려보면 다음과 같다.

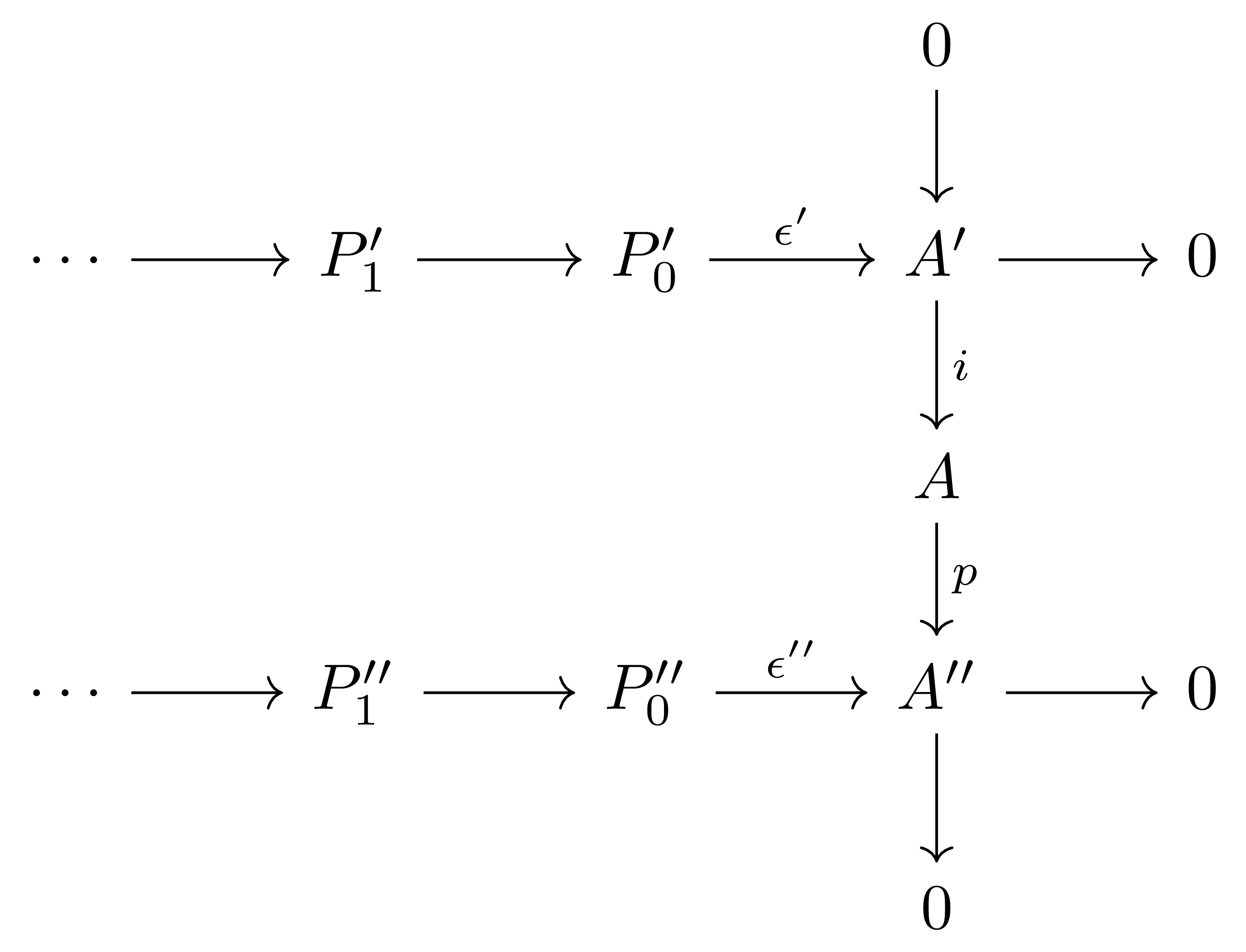
이제 \(P_0''\)이 projective라는 조건으로부터 \(P_0'' \rightarrow A\)을 정의할 수 있다. 한편 \(P_0' \rightarrow A\)는 \(i_A\)와 \(\epsilon'\)의 합성으로 이미 주어지므로, 이들의 direct sum을 생각하면 \(\epsilon:P_0 \rightarrow A\)를 얻는다. 이제 §Diagram chasing, ⁋보조정리 5으로부터 다음의 diagram

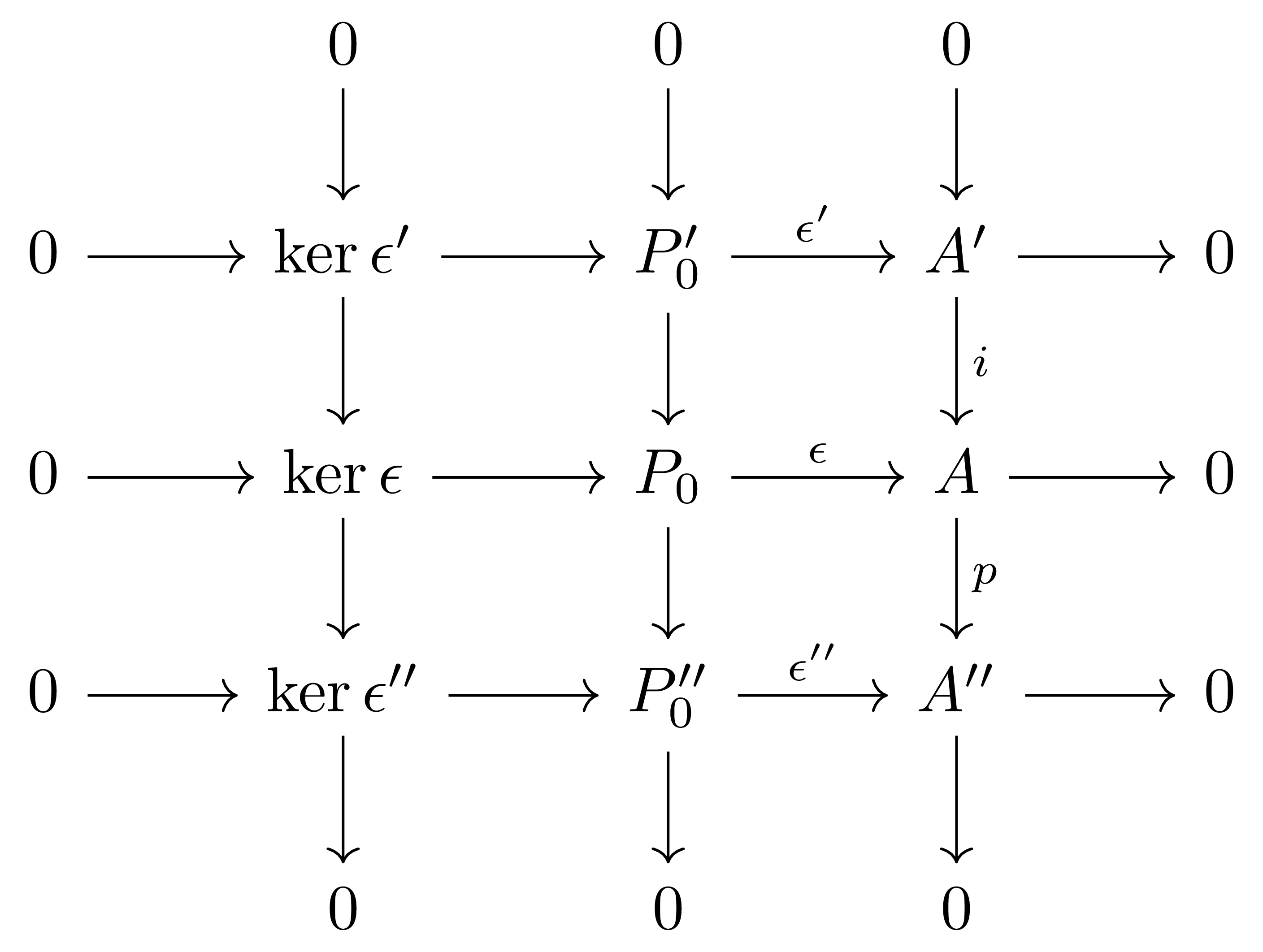
을 얻고, 특히 다음의 diagram

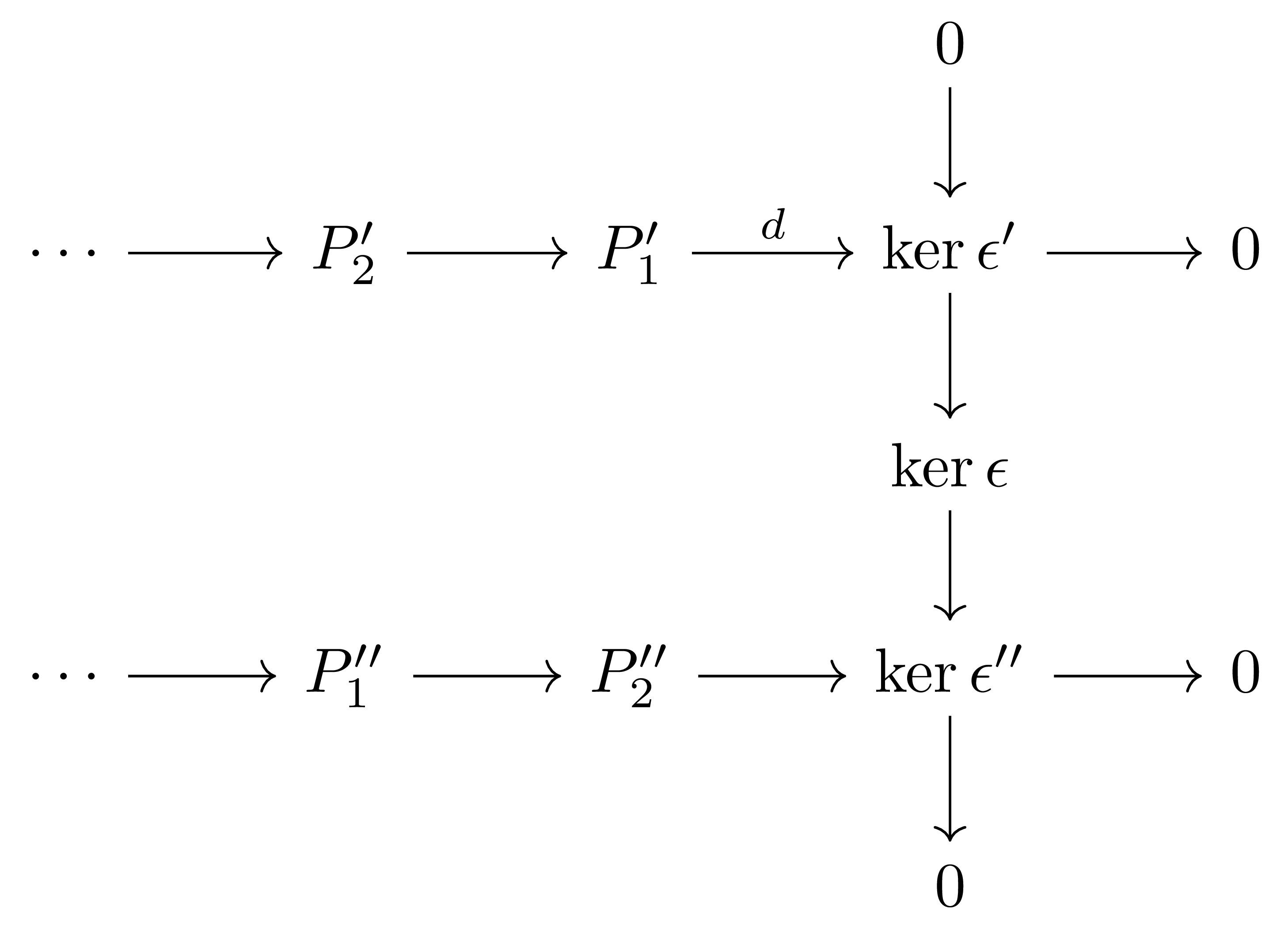
을 얻게 된다. 이 과정을 반복하여 \(P_\bullet\)을 얻는다.