K

Grad. student in mathematics

복잡한 대수적 구조를 다룰 때 유효한 전략 중 하나는 이 구조를 직접 분석하는 대신, 주어진 대수적 대상이 다른 대수적 대상에 어떻게 작용하는지를 살펴보는 것이다. 우리는 특별히 군의 작용에 관심이 있는데, 언제나 그렇듯 조금 더 일반적으로 모노이드가 집합 위에 작용하는 경우를 먼저 생각한다.

집합 위에 작용하는 모노이드Permalink

정의 1 Monoidal category (A,⊗,I)(\mathcal{A},\otimes, I)와 A\mathcal{A}의 monoid object (A,⋅,1)(A,\cdot, 1)를 고정하자. 그럼 morphism ρ:A⊗E→E\rho: A\otimes E\rightarrow E이 대상 E∈obj⁡(A)E\in\obj(\mathcal{A}) 위에 정의된 AA의 left action왼쪽 작용이라는 것은 다음 두 diagram이 모두 commute하는 것이다.

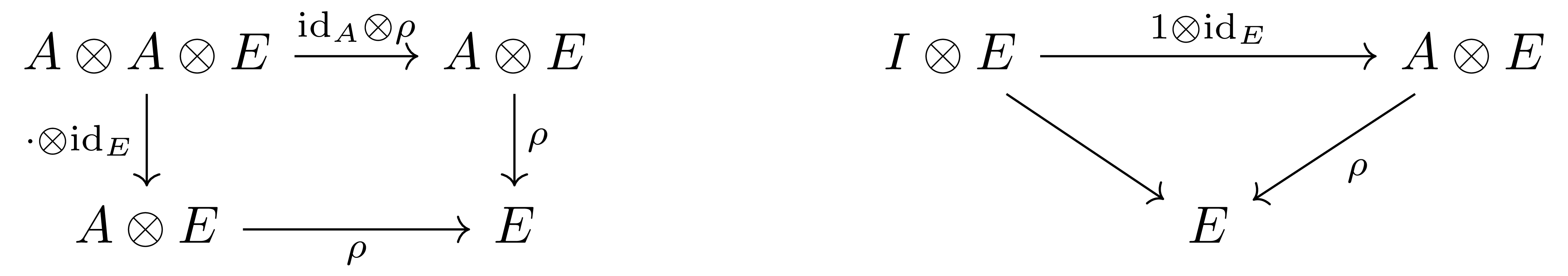
left_module

여기서 I⊗E→EI\otimes E \rightarrow E는 left unitor이다. 이 상황을 A↻EA\circlearrowright E로 적는다.

비슷하게, morphism ρ:E⊗A→E\rho: E\otimes A\rightarrow E이 대상 E∈obj⁡(A)E\in\obj(\mathcal{A}) 위에 정의된 AA의 right action오른쪽 작용이라는 것은 다음 두 diagram이 모두 commute하는 것이다.

right_module

마찬가지로 E⊗I→EE\otimes I \rightarrow E는 right unitor이다. 이 상황을 E↺AE \circlearrowleft A로 적는다.

Monoidal category (Set,×,I)(\Set,\times, I) 위의 monoid object (M,⋅,1)(M,\cdot,1)을 고정하자. 그럼 이를 통해 임의의 집합 EE 위에 정의된 MM의 left action을 생각할 수 있다. 그럼 [집합론] §집합의 곱, ⁋명제 4로부터

Hom⁡Set(M×E,E)≅Hom⁡Set(M,Hom⁡Set(E,E))≅Hom⁡Set(M,End⁡(E))\Hom_\Set(M\times E,E)\cong\Hom_\Set(M,\Hom_\Set(E,E))\cong\Hom_\Set(M, \End(E))

이므로, 임의의 left action은 함수 M→End⁡(E)M \rightarrow \End(E)를 정의한다. 그럼 정의 1의 두 diagram이 commutative라는 것은 이 함수가 실은 monoid homomorphism이라는 것과 같다.

바꿔 말하자면 MM이 EE에 왼쪽에서 act한다는 것은 임의의 α,β∈M\alpha,\beta\in M과 x∈Ex\in E에 대하여, 다음의 식

(αβ)⋅x=α⋅(β⋅x),e⋅x=x(\alpha\beta)\cdot x=\alpha\cdot(\beta\cdot x),\qquad e\cdot x=x

이 성립하는 것이다.

일반적인 경우, 우리는 위와 같이 주어진 대상이 다른 대상에 왼쪽에서 act하는 경우를 생각하지만, 종종 오른쪽에서 act하는 것이 자연스러울 때도 있다. 이는 다음 정의에 의해 사실은 같은 것이다.

정의 2 임의의 마그마 (M,∗)(M,\ast)에 대하여, MM의 opposite magma반대 마그마 (Mop,∗op)(M^\op,\ast^\op)는 다음과 같이 정의된 마그마이다.

  1. 집합으로서 Mop=MM^\op=M이다.
  2. 임의의 x,y∈Aopx,y\in A^\op에 대하여, x∗opyx\ast^\op y는 y∗xy\ast x로 정의된다.

그럼 right MM-action은 left MopM^\op-action과 같은 것임을 확인할 수 있다. 이를 다시 쓰자면

x⋅(βα)=(x⋅β)⋅α,x⋅e=xx\cdot(\beta\alpha)=(x\cdot\beta)\cdot\alpha,\qquad x\cdot e=x

라 할 수 있다. 이렇게 left action과 right action은 표기상의 차이일 뿐, 본질적으로는 동일한 의미를 갖는다. 따라서 앞으로 일반적인 이론을 전개할 때는 모든 action이 left action인 것으로 생각한다.

예시 3 Monoid MM과 MM-set EE가 주어졌다 하자. 그럼 P(E)\mathcal{P}(E)도 자연스러운 MM-set 구조를 갖는다. 임의의 α∈M\alpha\in M과 A∈P(E)A\in \mathcal{P}(E)에 대하여, α⋅A\alpha\cdot A를 다음 식

α⋅A={α⋅a∣a∈A}\alpha\cdot A=\{\alpha\cdot a\mid a\in A\}

으로 정의하자. 그럼

(αβ)⋅A={(αβ)⋅a∣a∈A}={α⋅(β⋅a)∣a∈A}=α⋅{β⋅a∣a∈A}=α⋅(β⋅A)(\alpha\beta)\cdot A=\{(\alpha\beta)\cdot a\mid a\in A\}=\{\alpha\cdot(\beta\cdot a)\mid a\in A\}=\alpha\cdot\{\beta\cdot a\mid a\in A\}=\alpha\cdot(\beta\cdot A)

이므로 이것이 P(E)\mathcal{P}(E) 위에 MM-action을 정의한다.

논의의 편의를 위해 다음과 같이 정의한다.

정의 4 Monoid MM이 집합 EE 위에 left action을 정의할 때, EE와 이 action을 통틀 (left) MM-set이라 부른다.

MM-set homomorphismPermalink

정의 5 Monoid MM이 고정되었다 하고, E,E′E,E’가 MM-set들이라 하자. 함수 f:E→E′f:E\rightarrow E’가 MM-set homomorphism이라는 것은 모든 x∈Ex\in E와 α∈M\alpha\in M에 대하여

f(α⋅x)=α⋅f(x)f(\alpha\cdot x)=\alpha\cdot f(x)

이 성립하는 것이다.

어렵지 않게 MM-set homomorphism들의 합성이 MM-set homomorphism이고, 또 항등함수가 MM-set homomorphism인 것을 확인할 수 있다. 즉, (left) MM-set들의 모임은 카테고리를 이룬다. 이를 MSet\lset{M}으로 적는다.

임의의 monoid homomorphism ϕ:M→M′\phi:M \rightarrow M’을 고정하자. 그럼 임의의 M′M’-set EE에 대하여, 다음 합성

M⟶ϕM′⟶ρEnd⁡(E)M\overset{\phi}{\longrightarrow}M'\overset{\rho}{\longrightarrow}\End(E)

을 통해 EE를 MM-set으로 생각할 수 있다. 이렇게 정의되는 action을 ϕ∗ρ\phi^\ast\rho라 적자. 그럼 명시적으로 ϕ∗ρ\phi^\ast\rho는 임의의 α∈M\alpha\in M과 x∈Ex\in E에 대해,

(ϕ∗ρ)(α)(x)=ρ(ϕ(α))(x)(\phi^\ast\rho)(\alpha)(x)=\rho(\phi(\alpha))(x)

으로 정의되는 action이다. 이제 두 M′M’-action ρ:M′→End⁡(E)\rho:M’ \rightarrow \End(E)와 ρ′:M′→End⁡(E)\rho’:M’ \rightarrow \End(E)가 주어졌다 하고, 이들 사이의 M′M’-homomorphism f:E→E′f:E \rightarrow E’가 주어졌다 하자. 그럼 임의의 α∈M\alpha\in M과 x∈Ex\in E에 대하여,

f((ϕ∗ρ)(α)(x))=f(ρ(ϕ(α))(x))=ρ′(ϕ(α))(f(x))=(ϕ∗ρ′)(f(x))f((\phi^\ast\rho)(\alpha)(x))=f(\rho(\phi(\alpha))(x))=\rho'(\phi(\alpha))(f(x))=(\phi^\ast\rho')(f(x))

이 성립한다. 즉 임의의 monoid homomorphism ϕ:M→M′\phi:M \rightarrow M’은 M′Set\lset{M’}에서 MSet\lset{M}으로의 functor를 정의한다. 툭별히 ι\iota가 submonoid의 inclusion이라면 이는 monoid action의 restriction이 된다.

한편, (Ei)(E_i)들이 MM-set들의 모임이면 이들의 product ∏Ei\prod E_i에 다음의 식

α⋅(xi)i∈I=(α⋅xi)i∈I\alpha\cdot(x_i)_{i\in I}=(\alpha\cdot x_i)_{i\in I}

을 통해 MM의 action을 정의한 것이 다시 MM-set이 된다. 이와 비슷하게 MM-set EE의 부분집합 FF가 다음의 식

x∈F  ⟹  α⋅x for all α∈Fx\in F\implies \alpha\cdot x\text{ for all $\alpha\in F$}

을 만족한다면 FF를 MM-subset이라 부른다. 또, MM-set 위에 정의된 동치관계 ∼\sim이 MM의 action과 compatible하다면, 즉

x∼y  ⟹  α⋅x∼α⋅yx\sim y\implies\alpha\cdot x\sim\alpha\cdot y

가 항상 참이라면 E/∼E/\mathnormal{\sim}은 자연스러운 MM-set의 구조를 갖는다.

Stabilizer, fixerPermalink

정의 6 MM-set EE의 부분집합 AA가 주어졌다 하자.

  • AA의 stabilizer안정자는 αA⊆A\alpha A\subseteq A를 만족하는 α\alpha들의 집합을 뜻하고, 이를 stab⁡(A)\stab (A)로 적는다.
  • AA의 strict stabilizer강한 안정자는 αA=A\alpha A=A를 만족하는 α\alpha들의 집합을 뜻하고, 이를 Stab⁡(A)\Stab(A)로 적는다.
  • AA의 fixer고정자는 모든 a∈Aa\in A에 대해 αa=a\alpha a=a를 만족하는 α\alpha들의 집합을 뜻하며, 이를 Fix⁡(A)\Fix(A)로 적는다.

임의의 부분집합 AA에 대하여 Fix⁡(A)⊆Stab⁡(A)⊆stab⁡(A)\Fix(A)\subseteq \Stab(A)\subseteq \stab(A)가 성립한다. 또, e∈Fix⁡(A)e\in\Fix(A)임이 자명하다.

명제 7 MM-set EE와 그 부분집합 AA에 대하여, stab⁡(A)\stab(A), Stab⁡(A)\Stab (A)와 Fix⁡(A)\Fix(A)는 MM의 submonoid이다.

증명

이들 집합이 연산에 대해 닫혀있음만 보이면 충분하다. 만일 α,β∈stab⁡(A)\alpha,\beta\in\stab(A)라 하면,

(αβ)A=α(βA)⊆αA⊆A(\alpha\beta)A=\alpha(\beta A)\subseteq \alpha A\subseteq A

으로부터 αβ∈stab⁡(A)\alpha\beta\in \stab(A)임을 안다. 비슷하게 만일 α,β∈Stab⁡(A)\alpha,\beta\in\Stab(A)라 하면,

(αβ)A=α(βA)=αA=A(\alpha\beta)A=\alpha(\beta A)=\alpha A=A

이므로 αβ∈Stab⁡(A)\alpha\beta\in \Stab(A)이고 주장이 성립한다. 마지막으로 만일 α,β∈Fix⁡(A)\alpha,\beta\in\Fix(A)라면 임의의 a∈Aa\in A에 대해

(αβ)a=α(βa)=αa=a(\alpha\beta)a=\alpha(\beta a)=\alpha a=a

이므로 αβ∈Fix⁡(A)\alpha\beta\in \Fix(A)이다.

따름정리 8 Group GG가 주어졌다 하자. GG-set EE와 그 부분집합 AA에 대하여, Stab⁡(A)\Stab (A)와 Fix⁡(A)\Fix(A)는 GG의 subgroup이며, 특히 Fix⁡(A)\Fix(A)는 Stab⁡(A)\Stab(A)의 normal subgroup이다.

증명

첫 번째 주장은 주어진 집합들이 역원에 대해 닫혀있음만 보이면 충분하고, 이는 임의의 α∈Stab⁡(A)\alpha\in\Stab(A)에 대해 다음 식

A=(α−1α)A=α−1(αA)=α−1AA=(\alpha^{-1}\alpha)A=\alpha^{-1}(\alpha A)=\alpha^{-1}A

이 성립하고, 임의의 α∈Fix⁡(A)\alpha\in\Fix(A)와 a∈Aa\in A에 대해

a=(α−1α)a=α−1(αa)=α−1aa=(\alpha^{-1}\alpha)a=\alpha^{-1}(\alpha a)=\alpha^{-1}a

이 성립하는 것으로부터 자명하다. 두 번째 주장은 임의의 α∈Fix⁡(A)\alpha\in\Fix(A), β∈Stab⁡(A)\beta\in\Stab(A)가 주어졌다 하고, 임의의 a∈Aa\in A에 대해 (βαβ−1)a(\beta\alpha\beta^{-1})a를 계산해보면

(βαβ−1)a=β(α(β−1a))=ββ−1a=a(\beta\alpha\beta^{-1})a=\beta(\alpha(\beta^{-1}a))=\beta\beta^{-1}a=a

이므로 βαβ−1∈Fix⁡(A)\beta\alpha\beta^{-1}\in\Fix(A)가 되어 성립한다.

위의 따름정리의 증명으로부터, group GG가 집합 EE에 act할 때, ρg\rho_g는 반드시 전단사임을 안다. 즉 im⁡ρ⊆Aut⁡(E)\im\rho\subseteq \Aut(E)가 항상 성립한다.

내부자기동형사상Permalink

이제 우리는 집합 EE 위에 추가적인 구조가 주어진 경우를 생각한다. 가령 EE 또한 monoid 구조를 가진다 하고, 주어진 monoid MM이 EE 위에 act한다 하면, MM-action은 monoid homomorphism M→End⁡(E)=End⁡Mon(E)M \rightarrow\End(E)=\End_\Mon(E)로 주어진다.

특별히 group GG가 자기 자신 위에 act하는 경우를 생각하자. 즉 ρ:G→End⁡(G)=End⁡Grp(G)\rho:G\rightarrow\End(G)=\End_\Grp(G)가 주어져 있다 하면, 따름정리 8의 증명으로부터 ρ\rho의 image는 모두 전단사라는 것을 안다. 그런데 전단사인 group homomorphism은 항상 group isomorphism이므로 (§대수적 구조, ⁋정의 6) GG가 자기 자신 위에 act한다면 이는 반드시 group homomorphism G→Aut⁡(G)G \rightarrow \Aut(G)와 같은 형태로 나타나야 한다는 것을 안다.

자기 자신 위에서 정의된 group action 중 특히 다음의 예시는 기억해둘 만한 가치가 있다.

명제 9 Group GG의 임의의 원소 gg에 대하여, ρg∈Aut⁡(G)\rho_g\in\Aut(G)를 다음의 식

ρg(x)=gxg−1\rho_g(x)=gxg^{-1}

으로 정의하면 대응 ρ:g↦ρg\rho:g\mapsto \rho_g는 group homomorphism이 된다.

증명

임의의 x,y∈Gx,y\in G에 대하여

ρg(xy)=g(xy)g−1=(gxg−1)(gyg−1)=ρg(x)ρg(y)\rho_g(xy)=g(xy)g^{-1}=(gxg^{-1})(gyg^{-1})=\rho_g(x)\rho_g(y)

가 성립하는 것으로부터 ρg\rho_g가 group homomorphism이라는 것을 안다. 따라서 im⁡ρ⊆Aut⁡(G)\im\rho\subseteq\Aut(G)가 성립한다.

한편 임의의 g,h∈Gg,h\in G와 x∈Gx\in G에 대하여,

ρgh(x)=(gh)x(gh)−1=g(hxh−1)g−1=(ρg∘ρh)(x)\rho_{gh}(x)=(gh)x(gh)^{-1}=g(hxh^{-1})g^{-1}=(\rho_g\circ\rho_h)(x)

이므로 ρgh=ρg∘ρh\rho_{gh}=\rho_g\circ\rho_h이다. 즉, ρ:g↦ρg\rho:g\mapsto \rho_g는 GG에서 Aut⁡(G)\Aut(G)로의 group homomorphism이다.

정의 10 Group GG가 주어졌다 하자. 명제 9의 automorphism ρg\rho_g를 gg에 의해 정의되는 inner automorphism내부자기동형사상이라 부르고, 이들의 모임을 Inn⁡(G)\Inn(G)로 적는다.

명제 11 Group GG에 대하여, inner automorphism들의 모임 Inn⁡(G)\Inn(G)는 Aut⁡(G)\Aut(G)의 normal subgroup이다.

증명

Inn⁡(G)\Inn(G)는 group homomorphism ρ:G→Aut⁡(G)\rho:G\rightarrow\Aut(G)의 image이므로 Aut⁡(G)\Aut(G)의 subgroup인 것은 자명하며, 따라서 Inn⁡(G)\Inn(G)가 normal subgroup임만 보이면 충분하다.

임의의 f∈Aut⁡(G)f\in\Aut(G)를 택하고, g∈Gg\in G를 임의로 고정하자. f∘ρg∘f−1∈Inn⁡(G)f\circ\rho_g\circ f^{-1}\in \Inn(G)임을 보여야 한다. 이는 임의의 x∈Gx\in G에 대하여,

(f∘ρg∘f−1)(x)=f(gf−1(x)g−1)=f(g)xf(g−1)=ρf(g)(x)(f\circ\rho_g\circ f^{-1})(x)=f(gf^{-1}(x)g^{-1})=f(g)xf(g^{-1})=\rho_{f(g)}(x)

이므로 자명하다.

한편, ρ:G→Inn⁡(G)\rho:G\rightarrow\Inn(G)는 전사이며, 따라서 first isomorphism theorem에 의하여

G/ker⁡ρ≅Inn⁡(G)G/\ker\rho\cong\Inn(G)

가 성립한다. ker⁡ρ\ker\rho에도 특별한 이름이 있다.

정의 12 Group GG와, 명제 9에서 정의한 group homomorphism ρ:G→Inn⁡(G)\rho:G\rightarrow\Inn(G)에 대하여, ker⁡ρ\ker\rho를 GG의 center중심이라 부르고 C(G)C(G)로 표기한다.

정의에 의하여,

g∈ker⁡ρ  ⟺  ρg=idG  ⟺  gxg−1=xfor all x∈Gg\in\ker\rho\iff\rho_g=\id_G\iff gxg^{-1}=x\quad\text{for all $x\in G$}

이므로, GG가 inner automorphism으로 자기 자신 위에 작용하는 상황에서의 fixer Fix⁡(G)\Fix(G)가 정확히 C(G)C(G)이다. 더 일반적으로, 임의의 부분집합 A⊆GA\subseteq G에 대하여 AA의 fixer Fix⁡(A)\Fix(A)를 AA의 centralizer CG(A)C_G(A)로 정의한다. 이와 비슷하게 AA의 normalizer NG(A)N_G(A)를 Stab⁡(A)\Stab(A)로 정의한다.

궤도-안정자 정리Permalink

이제 다시 우리는 일반적인 집합 EE 위에 정의된 group action을 생각한다. 우선 다음을 정의하자.

정의 13 집합 EE 위에 group GG의 action이 정의되었다 하자. 그럼 원소 x∈Ex\in E의 orbit은 다음의 집합

G⋅x={g⋅x∣g∈G}G\cdot x=\{g\cdot x\mid g\in G\}

으로 주어진다.

그럼 EE 위에 정의된 다음의 relation

x∼y  ⟺  G⋅x=G⋅y(∗)x\sim y\iff G\cdot x=G\cdot y\tag{$\ast$}

은 equivalence relation이므로 quotient set E/∼E/{\sim}이 정의되며, 이는 orbit들로 이루어진 집합이다.

정리 14 (Orbit-stabilizer theorem) 집합 EE 위에 group GG의 action이 주어졌다 하자. 그럼 다음의 식

∣G⋅x∣=[G:Stab⁡(x)]\lvert G\cdot x\rvert=[G:\Stab(x)]

이 성립한다.

증명

함수 p:G→G⋅xp:G \rightarrow G\cdot x를 g↦g⋅xg\mapsto g\cdot x로 정의하면 G⋅xG\cdot x의 정의에 의해 이 함수는 surjective이다. 한편, p(g1)=p(g2)  ⟺  g1−1g2∈Stab⁡(x)p(g_1)=p(g_2)\iff g_1^{-1}g_2\in \Stab(x)이므로 [집합론] §동치관계의 예시들, ⁋명제 7 이후의 canonical decomposition으로부터 원하는 결과를 얻는다.

따라서, 만일 GG가 finite이라면 §몫군, ⁋명제 5에 의하여 다음의 식

∣G⋅x∣=∣G∣∣Stab⁡(x)∣(∗∗)\lvert G\cdot x\rvert=\frac{\lvert G\rvert}{\lvert\Stab(x)\rvert}\tag{$\ast\ast$}

을 얻는다.

마찬가지로 GG가 finite이라 하고, GG가 유한집합 EE 위에 act한다 하자. EgE^g를 gg에 의해 고정되는 원소들

Eg={x∈E∣g⋅x=x}E^g=\{x\in E\mid g\cdot x=x\}

로 정의하면

∑g∈G∣Eg∣=#{(g,x)∈G×E:g⋅x=x}=∑x∈X∣Stab⁡(x)∣\sum_{g\in G}\lvert E^g\rvert=\# \{(g, x)\in G\times E: g\cdot x=x\}=\sum_{x\in X}\lvert \Stab(x)\rvert

이 성립한다. 이제 (∗∗\ast\ast)로부터

∑x∈X∣Stab⁡(x)∣=∑x∈X∣G∣∣G⋅x∣\sum_{x\in X}\lvert \Stab(x)\rvert=\sum_{x\in X}\frac{\lvert G\rvert}{\lvert G\cdot x\rvert}

이다. 한편 (∗\ast)로부터 정의되는 quotient set E/∼E/{\sim}을 생각하면, 위의 합은 다시

∑x∈X∣G∣∣G⋅x∣=∣G∣∑O∈E/∼∑x∈O1∣O∣=∣G∣∑O∈E/∼1=∣G∣∣E/∼∣\sum_{x\in X}\frac{\lvert G\rvert}{\lvert G\cdot x\rvert}=\lvert G\rvert\sum_{O\in E/{\sim}}\sum_{x\in O}\frac{1}{\lvert O\rvert}=\lvert G\rvert\sum_{O\in E/{\sim}} 1=\lvert G\rvert\lvert E/{\sim}\rvert

로 쓸 수 있다. 이로부터 다음 보조정리를 얻는다.

보조정리 15 Finite group GG가 유한집합 EE 위에 act한다고 하고, E/∼E/{\sim}을 orbit들로 이루어진 EE의 quotient set이라 하자. 그럼 다음의 식

∣E/∼∣=1∣G∣∑g∈G∣Eg∣\lvert E/{\sim}\rvert=\frac{1}{\lvert G\rvert}\sum_{g\in G}\lvert E^g\rvert

이 성립한다.

참고문헌

[Bou] Bourbaki, N. Algebra I. Elements of Mathematics. Springer. 1998.

댓글남기기