우리는 앞선 글에서 monoid의 정의를 살펴보았는데, 대표적으로 집합론에서 정의한 자연수는 덧셈에 대한 commutative monoid가 된다. 이번 글에서 우리는 commutative semigroup으로부터 abelian group을 얻어내는 방법을 소개한다.
우선 abelian group들의 category $\Ab$를 생각하면, 임의의 abelian group은 그 역원에 대한 정보를 잊어버리면 commutative monoid로 볼 수 있으므로 forgetful functor $U: \Ab \rightarrow \cMon$이 존재한다. 이 functor는 left adjoint $K:\cMon \rightarrow \Ab$를 갖는 것이 알려져 있으며, 이 adjunction을 풀어 쓰면 다음의 식
\[\Hom_\Ab(K(M), G)\cong\Hom_\cMon(M, U(G))\]이다. 즉 commutative monoid $M$과, monoid homomorphism $M\rightarrow U(G)$가 주어졌을 때 유일한 group homomorphism $K(M)\rightarrow G$를 얻어낼 수 있어야 한다.
Universal mapping problem
이제 위에서 설명한 left adjoint $K$의 존재성을 보여야 한다. 우리는 더 일반적으로, 메인 레퍼런스인 [Bou]를 따라 commutative semigroup에서 abelian group을 얻어내는 과정을 살펴본다. 한편, adjunction의 unit을 이용하면 $K$가 만족해야 하는 성질을 풀어 쓸 수 있다.
Abelian group $K(S)$와 semigroup homomorphism $\eta_S:S\rightarrow K(S)$는 다음과 같은 성질을 만족하는 쌍이다.
(Universal mapping problem) 임의의 abelian group $G$와, 임의의 semigroup homomorphism $f:S\rightarrow G$가 주어질 때마다 group homomorphism $\bar{f}:K(S)\rightarrow G$가 유일하게 존재하여 $f=\bar{f}\circ\eta_S$이 성립한다.
이를 직관적으로 해석하면 $K(S)$는 $(S,+)$를 포함하는 가장 작은 abelian group이라 생각할 수 있다.
위의 성질을 만족하는 $K(S)$는 isomorphism에 대해 유일하다.
명제 1 Abelian group $H$와 semigroup homomorphism $\eta_S’$가 위의 universal mapping problem을 만족한다면, $K(S)\cong H$가 성립한다.
증명
우선 다음 diagram을 살펴보자.
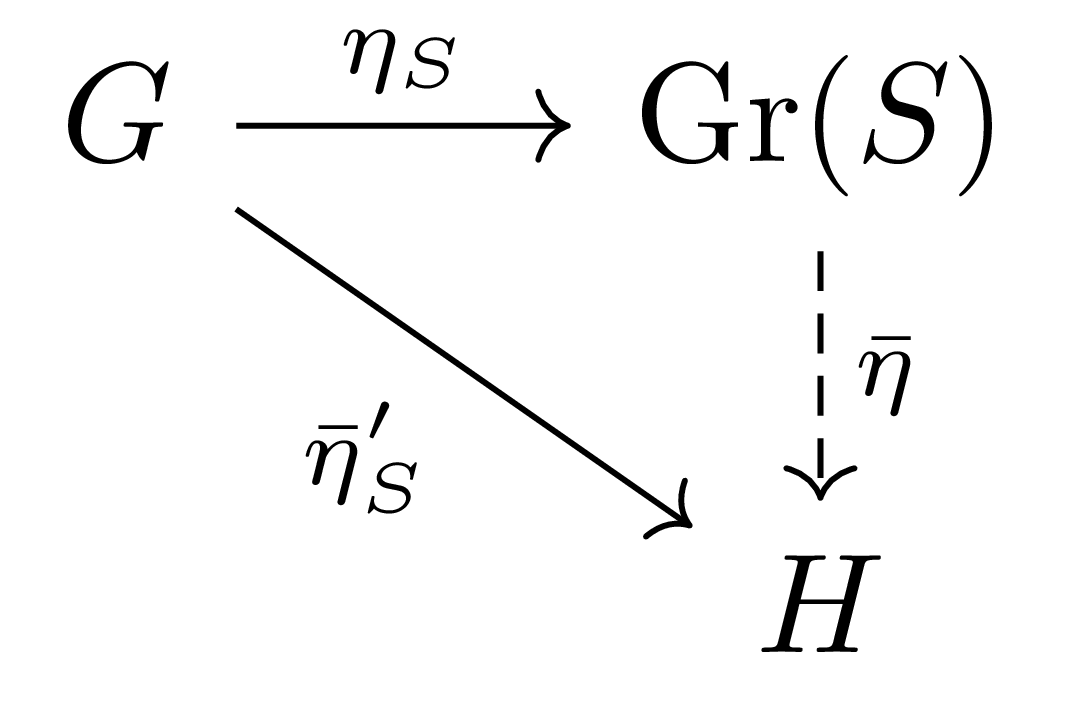
그럼 universal property에서, $\eta_S’= \bar{\eta}_S’\circ\eta_S$이도록 하는 $\bar{\eta}_S’: K(S)\rightarrow H$가 존재한다. 한편, 다시 다음의 diagram
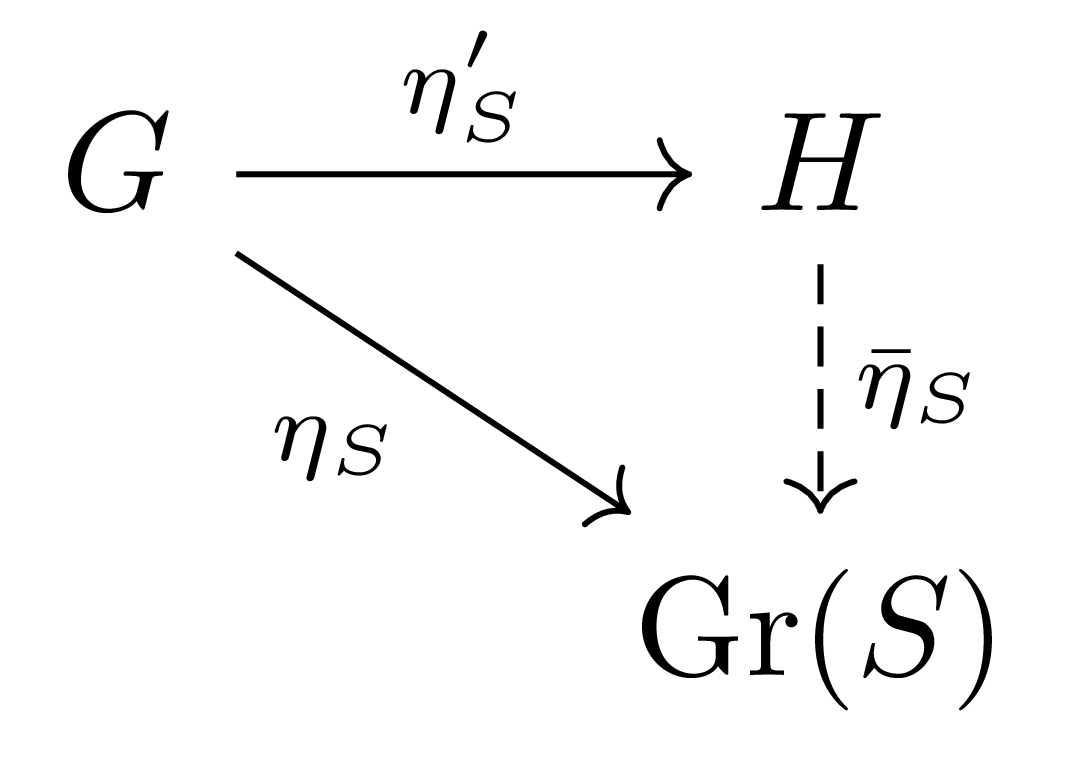
에서 $H$에 대한 universal property를 사용하면 $\eta_S=\bar{\eta}_S\circ\eta_S’$이도록 하는 $\bar{\eta}_S:H\rightarrow K(S)$가 존재한다. 그럼
\[\bar{\eta}_S'\circ\bar{\eta}_S\circ\eta_S'=\bar{\eta}_S'\circ \eta_S=\eta=\id_{H}\circ \eta_S'\]이고, 다시 universal property에 의하여 $f\circ \eta_S’=\eta_S’$를 만족하는 $f$는 유일하므로 $f=\id_H=\bar{\eta}_S’\circ \bar{\eta}_S$이 성립한다. 혹은, diagram의 언어로는, 다음 diagram을 commute하게 만드는 $H\rightarrow H$는 유일하므로 $\id_H=\bar{\eta}_S’\circ \bar{\eta}_S$여야 한다.

비슷하게 $\id_{K(S)}=\bar{\eta}_S\circ \bar{\eta}_S’$가 성립한다는 것도 보일 수 있고, 따라서 $K(S)\cong H$가 성립한다.
한편, $S$가 이미 abelian group이었다면, $K(S)$는 다른 원소를 추가할 필요 없이 $S$ 그 자체가 나와야 한다.
명제 2 만일 $S$가 abelian group이라면 위의 universal mapping problem을 만족하는 abelian group $K(S)$는 $K(S)\cong S$를 만족한다.
증명
$S$와 $\id_S$가 자명하게 universal property를 만족하므로, 앞선 명제 1에 의하여 universal property를 만족하는 임의의 abelian group은 $S$와 동형이어야 한다.
위의 두 명제들은 universal mapping problem을 만족하는 $K(S)$가 우리가 찾는 abelian group이라는 것을 보여주지만, 실제로 $K(S)$가 존재한다는 것은 보여주지 않는다.
$K(S)$의 정의
$S$가 abelian group이 될 수 없는 이유는 임의의 원소에 대한 역원이 존재하지 않을 수도 있기 때문이다. 직관적으로 이는
주어진 commutative semigroup $(S,+)$에 대하여, product semigroup $S\times S$를 생각하자. (§대수적 구조, ⁋예시 5) $S\times S$의 둘째 부분을 음수처럼 생각하면, 다음 식
\[(a_1, b_1)+(a_2, b_2)=(a_1+a_2, b_1+b_2)\]은 마치
\[(a_1+a_2)-(b_1+b_2)=(a_1-b_1)+(a_2-b_2)\]를 나타내는 것처럼 생각할 수 있다.
물론, 일반적으로 $a$와 $b$가 다르더라도 $a-b$의 값은 충분히 차이가 날 수 있기 때문에, 우리는 $S\times S$ 위에 동치관계 $R$을 다음과 같이 정의한다.
\[(a_1, b_1)\equiv (a_2, b_2)\pmod{R}\iff a_1+b_2+c=a_2+b_1+c\text{ for some $c\in S$}\]우선 이 관계가 동치관계임을 보여야 한다.
보조정리 3 위에서 정의한 관계 $R$은 product semigroup $S\times S$ 위에서의 연산과 compatible한 동치관계이다.
증명
우선, $R$이 동치관계임을 보이자. 임의의 $(a,b)\in S\times S$에 대하여,
\[a+b+c=a+b+c\]가 임의의 $c\in S$에 대해 성립하므로, $(a,b)\equiv(a,b)$이다. $(a_1,b_1)\equiv (a_2,b_2)$라 하자. 즉, 어떠한 $c\in S$에 대하여
\[a_1+b_2+c=a_2+b_1+c\]가 성립한다. 그런데 이는 정확히 $(a_2,b_2)\equiv (a_1,b_1)$의 조건이므로, $R$은 symmetric하다. 마지막으로, $(a_1,b_1)\equiv(a_2,b_2)$이고 $(a_2,b_2)\equiv (a_3,b_3)$이라 하자. 그럼 어떤 $c$, $c’$에 대하여
\[a_1+b_2+c=a_2+b_1+c,\qquad a_2+b_3+c'=a_3+b_2+c'\]가 성립한다. 이제 두 식을 더하면,
\[a_1+b_3+(a_2+b_2+c+c')=a_3+b_1+(a_2+b_2+c+c')\]이므로 $(a_1,b_1)\equiv(a_3,b_3)$이 성립한다. 즉, $R$은 동치관계가 된다.
이제 $R$이 $S\times S$의 연산과 compatible하다는 것을 보여야 한다. 이를 위해, $(a_1, b_1)\equiv(a_1’,b_1’)$이고 $(a_2, b_2)\equiv (a_2’,b_2’)$라 하자. 우리는 $(a_1+a_2, b_1+b_2)\equiv(a_1’+a_2’, b_1’+b_2’)$임을 보여야 한다. 주어진 조건으로부터, 적당한 $c_1$, $c_2$가 존재하여
\[a_1+b_1'+c_1=a_1'+b_1+c_1,\qquad a_2+b_2'+c_2=a_2'+b_2+c_2\]가 성립한다. 이제, 두 식을 더하면 \((a_1+a_2)+(b_1'+b_2')+(c_1+c_2)=(a_1'+a_2')+(b_1+b_2)+(c_1+c_2)\)
이 성립하므로, 정의에 의해 $(a_1+a_2, b_1+b_2)\equiv(a_1’+a_2’, b_1’+b_2’)\pmod{R}$이 성립하고, 따라서 $R$은 $S\times S$의 연산과 compatible하다.
그러므로 $(S\times S)/R$은 commutative semigroup이 된다. 이를 $K(S)$라 하자.
보조정리 4 $K(S)$는 abelian group이다.
증명
$K(S)$가 항등원과 역원을 가짐을 보이면 된다. 우리는 $(a,b)$를 $a-b$처럼 생각하고 있으므로, 항등원은 $(a,a)$, $(a,b)$의 역원은 $-(a-b)=b-a$, 즉 $(b,a)$가 될 것이다. 이를 증명하자.
우선, 임의의 $c\in S$에 대하여, $[(c,c)]$가 항등원이 됨을 보인다. 임의의 $[(a,b)]\in K(S)$에 대하여,
\[[(a,b)]+[(c,c)]=[(a+c, b+c)]\]가 성립한다. 그런데
\[(a+c)+b+d=(b+c)+a+d\]가 임의의 $d\in S$에 대해 성립하므로, $(a+c, b+c)\equiv (a,b)$이고 따라서 $[(a+c, b+c)]=[(a,b)]$가 성립한다. 교환법칙에 의하여 $[(c,c)]+[(a,b)]=[(a,b)]$도 당연하게 성립하므로, $[(c,c)]$는 $K(S)$의 항등원이 된다.
한편, 임의의 $[(a,b)]\in K(S)$에 대하여
\[[(a,b)]+[(b+a)]=[(a+b,a+b)]\]이므로, 앞선 논증에 의해 $[(a,b)]+[(b,a)]$는 $K(S)$의 항등원이 되고, $[(a,b)]+[(b,a)]$도 마찬가지다. 따라서 $K(S)$의 임의의 원소의 역원이 존재하므로, $K(S)$는 group의 구조를 가진다.
그럼 $K(S)$는 우리가 찾던 abelian group이 된다. 즉, $K(S)$는 위의 universal mapping problem을 만족한다.
명제 5 Commutative semigroup $(S, +)$에 대하여, 위와 같이 만들어진 가환군 $K(S)$와, 자연스러운 semigroup homomorphism $\eta_S:S\rightarrow K(S)$는 universal property를 만족한다.
증명
우선 $S$에서 $K(S)$로의 자연스러운 semigroup homomorphism이 무엇인지부터 생각해보자. 우리는 $K(S)$에서 $(a,b)$를 $a-b$로 취급하고 있으므로, $a$가 $K(S)$에서는 $(a+b)-b$, 즉 $[(a+b, b)]$인 것을 알 수 있다. 따라서 $\eta_S$을 $a\mapsto[(a+a, a)]$으로 정의하자. 물론 아무 $b$나 택해서 $a\mapsto[(a+b,b)]$으로 정의해도 같은 값이 나온다.
Universal property를 증명하기 위해, 임의의 abelian group $G$와, semigroup homomorphism $f:S\rightarrow G$가 주어졌다고 하자.
우선, 만약 주어진 성질을 만족하는 $\bar{f}:K(S)\rightarrow S$가 존재한다면, $\bar{f}$는 반드시 유일해야 한다. 임의의 $[(a,b)]$에 대하여,
\[\begin{aligned}\bar{f}\left([(a,b)]\right)&=\bar{f}\left([(a+(a+b), b+(a+b))]\right)=\bar{f}\left([(a+a,a)]+[(b, b+b)]\right)\\ &\bar{f}\left([(a+a, a)]\right)+\bar{f}\left([(b,b+b)]\right)=\bar{f}\left(\eta_S(a)\right)-\bar{f}\left(\eta_S(b)\right)\\ &=f(a)-f(b)\end{aligned}\]이므로, 각각의 원소들에서의 함수값이 유일하게 정해지기 때문이다.
이제 유일성 증명에서 힌트를 얻어, $\bar{f}([(a,b)])$를 $f(a)-f(a)$으로 정의하자. 우선, 이 정의는 잘 정의되어 있다. 즉, 만일 $(a_1,b_1)\equiv(a_2,b_2)$라면, $f(a_2)-f(b_2)=f(a_1)-f(b_1)$이 성립한다. $(a_1,b_1)\equiv(a_2,b_2)$이므로, 어떤 $c\in S$가 존재하여 $a_1+b_2+c=a_2+b_1+c$이고, 따라서
\[f(a_1)+f(b_2)+f(c)=f(a_1+b_2+c)=f(a_2+b_1+c)=f(a_2)+f(b_1)+f(c)\]이므로, 양 변에서 $f(c)$를 빼고 적당히 이항해서 정리해주면
\[f(a_1)-f(b_1)=f(a_2)-f(b_2)\]을 얻는다.
또, $\bar{f}$는 group homomorphism이 된다. 임의의 $[(a_1, b_1)]$, $[(a_2,b_2)]$에 대하여
\[\begin{aligned}\bar{f}\left([(a_1,b_1)]+[(a_2, b_2)]\right)&=\bar{f}\left([(a_1+a_2, b_1+b_2)]\right)=f(a_1+a_2)-f(b_1+b_2)\\&=f(a_1)+f(a_2)-f(b_1)-f(b_2)=(f(a_1)-f(b_1))+(f(a_2)-f(b_2))\\&=\bar{f}\left([(a_1, b_1)]\right)+\bar{f}\left([(a_2,b_2)]\right)\end{aligned}\]가 성립하기 때문이다.
마지막으로, $\bar{f}$가 주어진 조건 $f=\bar{f}\circ\eta_S$을 만족한다는 것은 계산해보면 자명하다.
이렇게, 우리는 원했던 abelian semigroup $K(S)$를 얻었다. 특히 정수를 엄밀한 방식으로 정의할 수 있다.
정의 6 Monoid $(\mathbb{N},+)$에 대하여, 위의 과정을 통해 얻어지는 abelian group을 $(\mathbb{Z},+)$으로 적는다.
Monoid of fractions
위의 논의에서 우리는 $S$의 모든 원소들의 역원을 추가하여 $K(S)$를 얻었다. 한편 정의 6을 살펴보면 우리가 실제로 하는 것은 $\mathbb{N}$의 부분집합 $\mathbb{N}\setminus\{0\}$의 원소들의 역원만 추가하는 것이다. 이 또한 위의 논의들을 약간 수정하면 얻어질 수 있는데, 증명은 생략하고 과정들만 살펴보자.
Commutative monoid $E$와 $E$의 부분집합 $S$, 그리고 $S$에 의해 생성되는 $E$의 submonoid $S’$를 생각하자. 또 $E$의 연산은 곱셈으로 적힌 것으로 생각한다. $E\times S’$ 위에 다음 관계
\[(a,p)\equiv (b,q)\pmod{R}\iff aqs=bps\text{ for some $s\in S'$}\]를 정의하면, 이 관계는 $E\times S’$ 위의 연산과 compatible한 동치관계이고 따라서 $(E\times S’)/R$이 monoid가 된다.
정의 7 위와 같이 얻어지는 monoid $(E\times S’)/R$을 $S$를 분모로 갖는 $E$의 monoid of fraction이라 부르고 $E_S$로 표기한다. 이 monoid의 원소 $(a,p)$는 $a/p$로 표기한다.
이 때, $E$는 monoid이므로 위의 논의와는 다르게 항등원 $1$을 가진다. 그럼 명제 5에서의 homomorphism $\eta_S$은 명시적으로, $a\mapsto a/1$로 생각할 수 있다.
참고문헌
[Bou] Bourbaki, N. Algebra I. Elements of Mathematics. Springer. 1998.

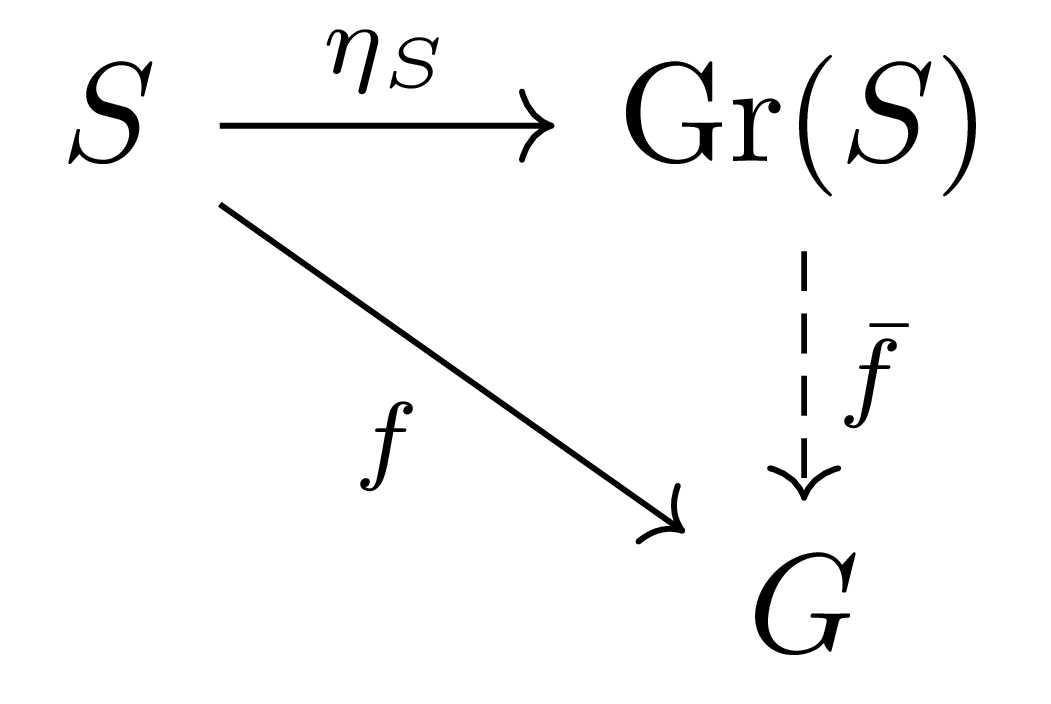
댓글남기기