집합의 곱
순서쌍을 가장 자연스럽게 일반화하는 것은 함수이다. 예컨대 $n$-tuple은 $I=\{1,2,\cdots, n\}$을 정의역으로 갖는, $i$를 넣으면 $i$번째 성분을 돌려주는 함수로 생각할 수 있다.
예컨대 집합 $A_1$, $A_2$에 대하여 $A_1\times A_2$은 순서쌍들 $(x_1,x_2)$의 모임이다. 위와 같이 순서쌍을 함수로 보자면, $A_1\times A_2$는 정의역 $\{1,2\}$를 갖는
그럼 일반적인 family의 곱은 다음과 같이 정의하는 것이 자연스럽다.
정의 1 $(A_i)_{i\in I}$가 집합들의 family라 하자. 그럼 $I$에서 $\bigcup A_i$로의 모든 함수들 중, $x_i=f(i)\in A_i$를 만족하는 것들의 모임 $P$를 이 family의 곱product이라 부른다.
집합들의 family를 표기할 때와 마찬가지로, $P$의 원소들을 $(x_i)_{i\in I}$로 적으며, 각각의 $x_i$를 $i$번째 성분이라 부르며, $F\in P$를 $F(i)$로 대응시키는 함수를 $i$번째 성분함수라 부르고 $\pr_i$로 적는다.
따라서 집합의 곱을 생각하는 것은
집합 $A,B$가 주어졌다고 하자. 그럼 $A$에서 $B$로의 함수는 $\mathcal{P}(A\times B)$의 원소이므로, 이들의 모임은 $\mathcal{P}(A\times B)$의 부분집합이 된다. 이를 우리는 $B^A$로 적는다. $A$에서 $B$로의 함수들의 집합을 $\Fun(A,B)$라 하자. 그럼 임의의 $F\in B^A$에 대하여, $f=(F,A,B)$는 $A$에서 $B$로의 함수이며, 이 대응 $F\mapsto f$는 $B^A$에서 $\Fun(A,B)$로의 함수이다.
한편, 임의의 함수 $f=(F,A,B)$에 대하여, $B^A$의 원소 $F$를 대응시키면 이 대응은 함수일 뿐만 아니라, 앞서 정의한 대응의 역함수임을 쉽게 확인할 수 있다. 즉 $B^A$와 $\Fun(A,B)$ 사이의 자연스러운 전단사함수가 존재하여 이 두 집합을 서로 같은 것으로 생각할 수 있다.
함수들 $u:A’\rightarrow A$와 $v:B\rightarrow B’$가 주어졌다고 하고, 다음의 diagram을 생각하자.

이 diagram에서, 어떤 함수 $f:A\rightarrow B$가 주어질 때마다 우리는 이에 해당하는 $A’$에서 $B’$로의 함수 $\tilde{f}=v\circ f\circ u$를 생각할 수 있다. 이 대응 $f\mapsto \tilde{f}$는 $\Fun(A, B)$에서 $\Fun(A’, B’)$로의 함수이다.
명제 2 위의 diagram에서, $u$가 전사함수고 $v$가 단사함수라면 $f\mapsto \tilde{f}$는 단사함수다. 만일 $u$가 단사함수고 $v$가 전사함수라면, $f\mapsto \tilde{f}$는 전사함수다.
증명
우선 $u$, $v$가 각각 전사함수와 단사함수라 하자. 주어진 함수 $f\mapsto\tilde{f}$가 단사임을 보이기 위해서는 $\tilde{f}=\tilde{g}$라면 $f=g$임을 보여야 한다. $s$와 $r$을 각각에 해당하는 section과 retraction이라 하자. 만일 $\tilde{f}=\tilde{g}$라면,
\[\begin{aligned} f&=\id_B\circ f\circ\id_A=(r\circ v)\circ f\circ(u\circ s)=r\circ(v\circ f\circ u)\circ s\\ &=r\circ\tilde{f}\circ s=r\circ\tilde{g}\circ s\\ &=r\circ(v\circ g\circ u)\circ s=(r\circ v)\circ g\circ (u\circ s)=\id_B\circ g\circ\id_A=g \end{aligned}\]이므로 $f=g$이다. 따라서 주어진 함수는 단사함수다.
비슷하게 $u$와 $v$가 각각 단사함수, 전사함수라 하자. 임의의 $f’\in\Fun(A’,B’)$에 대하여 $\tilde{f}=f’$인 $f\in\Fun(A,B)$가 존재함을 보여야 한다. $r’$, $s’$가 각각 $u$와 $v$의 retraction과 section이라 하자. 그럼
\[f'=\id_{B'}\circ f'\circ\id_{A'}=(v\circ s')\circ f'\circ(r'\circ u)=v\circ(s'\circ f'\circ r')\circ u\]이므로, $f=s’\circ f’\circ r’$는 $\Fun(A,B)$의 원소이며 $f’=\tilde{f}$를 만족한다. 따라서 주어진 함수는 전사함수다.
특별히 만일 $u$와 $v$가 모두 전단사라면 $f\mapsto \tilde{f}$ 또한 전단사함수가 된다.
앞서 집합들 사이의 합이 universal property를 만족했었는데, 마찬가지로 곱도 비슷한 universal property를 만족한다.
정리 3 집합들의 family $(A_i)$들의 곱 $P$와, 성분함수들 $\pr_i:P\rightarrow A_i$가 주어졌다 하자. 다른 집합 $B$와, 함수들 $f_i:B\rightarrow A_i$가 주어졌다고 하면, 식 $f_i=\pr_i\circ f$를 만족하도록 하는 유일한 함수 $f:B\rightarrow P$가 존재한다.
증명
우선 주어진 조건 $f_i=\pr_i\circ f$를 만족하는 함수 $f,f’$가 주어졌다 하자. 우리는 임의의 $y\in B$에 대해 $f(y)=f’(y)$임을 보여야 한다. 그런데 $f(y)$와 $f’(y)$는 어차피 $A$의 원소이므로 함수(순서쌍)이고, 따라서 $i$가 대응되는 값($i$번째 좌표)들에 의해 결정된다. 따라서 임의의 $y\in B$와 $i\in I$가 주어졌다고 할 때, $\pr_i(f(y))=\pr_i(f’(y))$라는 것을 보이면 충분하다. 그런데
\[\pr_i(f(y))=f_i(y)=\pr_i(f'(y))\]이므로, 그러한 함수 $f$는 유일해야 한다.
존재성의 경우, 마찬가지로 위의 유일성 증명에 힌트를 얻어 $f(y)$의 값을
$(f(y))(i)=f_i(y)$를 만족하는 함수 (혹은 $i$번째 좌표가 $f_i(y)$인 순서쌍)
으로 정의한 후 이 대응 $y\mapsto f(y)$가 실제로 함수임을 보이면 된다.
이제 정리 3의 조건을 만족하는 $(P, \pr_i)$가 적어도 하나는 존재하므로 (정의 1), 이를 곱집합의 정의로 삼아도 된다. 즉, $(A_i)_{i\in I}$들의 곱은 다음의 universal property를 만족하는 집합 $\prod_{i\in I} A_i$와 함수들 $\pr_i:\prod_{i\in I}A_i\rightarrow A_i$이라 할 수 있다.
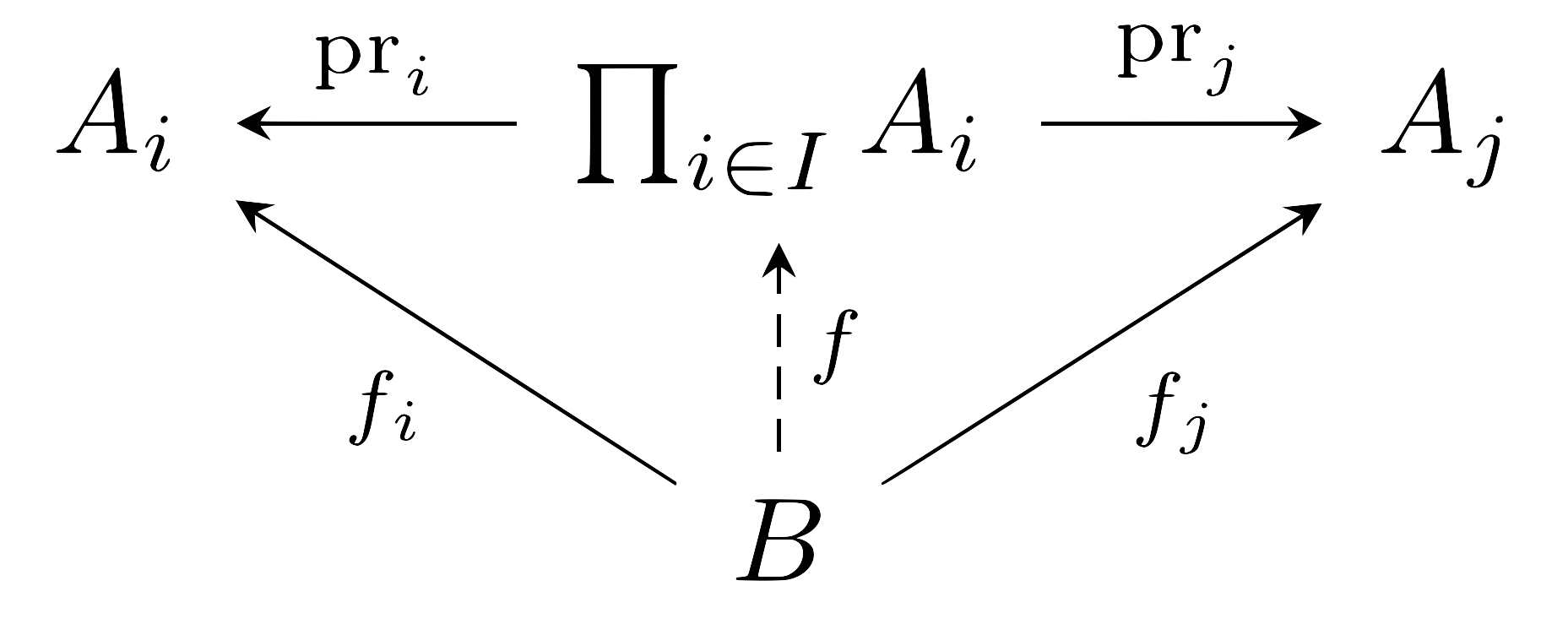
§집합의 합, ⁋따름정리 9와 정확하게 같은 논리를 펼치면 이 universal property를 만족하는 대상 및 $\pr_i$들 또한 전단사함수에 대해 유일함을 확인할 수 있다.
명제 4 집합 $A$, $B$, $C$에 대해 $f:B\times C\rightarrow A$라 하자. 만일 $\tilde{f}$가 $C$에서 $\Fun(B,A)$로의 함수 $y\mapsto f(-,y)$라면, $f\mapsto\tilde{f}$는 전단사함수이다. 즉, $\Fun(B\times C,A)$와 $\Fun(C, \Fun(B, A))$ 사이의 전단사함수가 존재한다.
증명
우선 $\tilde{f}$는 $C$에서 $\Fun(B,A)$로의 함수이므로, $\tilde{f}\in\Fun(C,\Fun(B,A))$이다. 따라서 주어진 함수는 $\Fun(B\times C, A)$에서 $\Fun(C, \Fun(B,A))$로의 함수이다. 우리는 이 함수가 전단사임을 보이기 위해 역함수를 만들 것이다.
$g\in\Fun(C, \Fun(B,A))$가 주어졌다고 하자. 그럼 임의의 $y\in C$에 대하여, $g(y)$는 $\Fun(B, A)$의 원소이다. 이제 $\bar{g}:B\times C\rightarrow A$를 $(x, y)$를 $g(y)(x)$로 보내는 함수로 정의하자. 그럼 임의의 $g\in \Fun(C,\Fun(B,A))$에 대하여, $g$를 $\bar{g}$로 보내는 함수
\[\begin{aligned} -:\Fun(C, \Fun(B,A))&\rightarrow\Fun(B\times C,A)\\ g\phantom{function}&\mapsto\phantom{function}\bar{g} \end{aligned}\]를 생각할 수 있다. 앞서 말한대로, 우리는 이 함수 $-$가 원래의 함수
\[\begin{aligned} \sim\;:\Fun(B\times C,A)&\rightarrow\Fun(C, \Fun(B,A))\\ f\phantom{function}&\mapsto\phantom{function}\tilde{f} \end{aligned}\]의 역함수임을 보여야 한다.
임의의 $f:B\times C\rightarrow A$에 대하여, $\tilde{f}\in \Fun(C, \Fun(B, A))$이다. 이제 이 함수를 거꾸로 $-$를 타고 $\Fun(B\times C,A)$로 보내자. 그럼 이 결과 $\bar{\tilde{f}}$는 $(x, y)$를 $\tilde{f}(y)(x)$로 보내는 함수이다. 그런데 $\tilde{f}(y)$는 함수 $f(-, y)$이므로 $\bar{\tilde{f}}=f$이다.
한편 임의의 $g\in\Fun(C, \Fun(B, A))$에 대하여, $\bar{g}$를 먼저 적용한 후 $\tilde{\bar{g}}$를 조사해보면, $\tilde{\bar{g}}$는 $y\mapsto \bar{g}(-,y)$로 정해지는 함수이다. 그런데 $\bar{g}$의 정의에 의하여 이는 다시 $y$를 $g(y)(-)$로 보내는 함수이다. 즉 $\tilde{\bar{g}}$는 다시 $g$가 된다. 이로부터 $\bar{\tilde{f}}=f$이고 $\tilde{\bar{g}}=g$이므로 이들은 서로 역함수 관계이다. 즉, 우리는 다음을 보인 것이다.
그러므로 $\sim\;:f\mapsto\tilde{f}$는 전단사이다.
우리는 합집합을 정의한 직후에, index set을 전사함수를 통해 바꾸어도 아무런 일도 일어나지 않음을 보았는데, 집합들의 곱에서는 전단사함수를 통해 바꾸어도 아무런 일도 일어나지 않는다.
명제 5 $(A_i)_{i\in I}$가 집합들의 family이고 $u:K\rightarrow I$가 전단사라 하자. 임의의 $f:I\rightarrow \prod_{i\in I}A_i$에 대해, 이를 $f\circ u: K\rightarrow \prod_{i\in I} A_i$로 보내는 함수 $f\mapsto f\circ u$는 전단사함수이다.
증명
다음의 diagram을 생각하자.

여기서 $v$는 $(x_i)_{i\in I}$를 $(x_{u(k)})_{k\in K}$로 대응시키는 전단사함수이다. 그럼 위의 명제 2에 의하여 $F\mapsto F\circ U$는 전단사다.
참고문헌
[HJJ] K. Hrbacek, T.J. Jeck, and T. Jech. Introduction to Set Theory. Lecture Notes in Pure and Applied Mathematics. M. Dekker, 1978.
[Bou] N. Bourbaki, Theory of Sets. Elements of mathematics. Springer Berlin-Heidelberg, 2013.

댓글남기기