K

Grad. student in mathematics

이번 글에서 우리는 다양한 맥락에서 등장하는 동치관계들의 예시를 살펴본다.

함수에 의해 정의되는 동치관계

앞선 글에서 동치관계 $(R,A,A)$에서부터 canonical한 함수 $p:A\rightarrow A/R$이 잘 정의된다는 것을 보았는데, 그 역 또한 성립한다. 즉, 임의의 함수가 주어졌을 때, 이 함수를 사용하여 동치관계를 만들 수 있다.

명제 1 집합 $A$와 이를 정의역으로 갖는 함수 $f$가 주어졌다 하자. 그럼 $x$, $y$ 사이의 관계 $x$, $y\in A$이고 $f(x)=f(y)$는 $A$ 위에서의 동치관계다.

증명

주어진 관계가 $A$ 위에서 reflexive함은 자명하다. 한편, 만일 $f(x)=f(y)$라면 $f(y)=f(x)$이고, $f(x)=f(y)$, $f(y)=f(z)$이면 $f(x)=f(z)$이므로 이 관계는 symmetric, transitive하기도 하다.

정의 2 위의 명제에서 정의된 동치관계를 $f$에 의해 정의된 동치관계라 부른다.

동치관계 $(R,A,A)$와 이로부터 유도된 $p:A\rightarrow A/R$에 대하여, 동치관계 $R$은 정의 2를 $p$에 적용하여 얻은 동치관계와 정확하게 같다는 것을 확인할 수 있다.

단항관계와 compatible한 동치관계

정의 3 $(R,A,A)$가 동치관계라 하자. 그럼 단항관계 $P$가 $R$과 compatible하다는 것은 $P(x)\wedge (x\sim_{\tiny R}y)\implies P(y)$인 것이다.

예를 들어, 단항관계

$x$는 짝수이다

는 동치관계

$x-y$가 4의 배수이다

와 compatible하다. Equivalence class의 관점에서 위 정의를 다시 쓰면 다음과 같다.

명제 4 $R$이 집합 $A$ 위에서의 동치관계이고, $P$가 $R$과 compatible한 단항관계라 하자. 그럼 $t\in A/R$이고 어떤 $x\in t$가 존재하여 $P(x)$인 것과 $t\in A/R$이고 모든 $x\in t$에 대하여 $P(x)$인 것이 서로 동치이다.

증명

풀어 쓰자면,

$P$가 $R$과 compatible할 때, equivalence class의 단 하나의 원소만 $P$를 만족한다면, 그 원소와 같은 class에 들어있는 모든 원소에 대해서도 $P$가 성립한다.

그리고 이건 정확히 compatible한 단항관계의 정의다.

반대 방향은 자명하다. 만일 $t\in A/R$에 대하여 $a\in t$가 존재하여 $P(a)$라 하자. 그럼 모든 $x\in t$에 대하여 $a\sim_{\tiny R}x$이므로 $P(x)$이다.

동치관계의 포화

정의 5 $R$이 $A$ 위에서의 동치관계이고 $X$가 $A$의 부분집합이라 하자. $X$가 $R$에 대해 saturated포화되었다는 것은 단항관계 $x\in A$가 $R$과 compatible한 것이다.

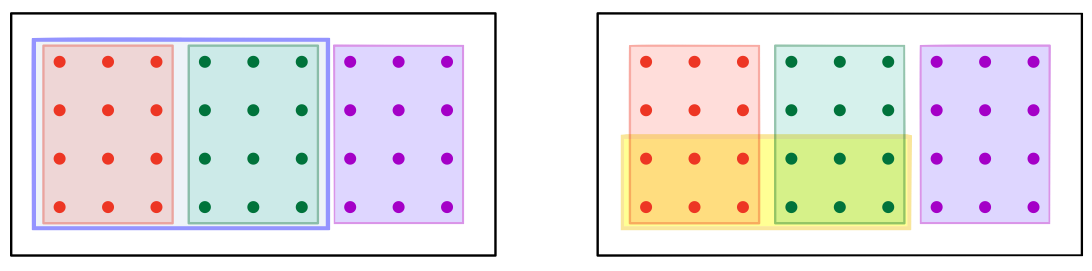
saturated_set

주어진 몫집합 (위쪽) 에서의 saturated subset (왼쪽)과 saturated가 아닌 부분집합 (오른쪽)

위의 정의에 따르면, 어떤 집합 $X$가 $R$-saturated이기 위해서는 $x\in X$라면 $R(x)\subseteq X$가 반드시 성립해야 한다. 따라서 $R$-saturated인 부분집합 $X$는 어떠한 부분집합 $B\subseteq A$에 대하여 $\bigcup_{x\in B}R(x)$로 나타낼 수 있는 집합이다. 이로부터 다음의 두 결과를 쉽게 확인할 수 있다.

  1. 만일 $(A_i)_{i\in I}$가 $R$-saturated인 부분집합들의 family라면, $\bigcup_{i\in I} A_i$와 $\bigcap_{i\in I} A_i$도 마찬가지다.
  2. $X\subseteq A$가 $R$-saturated라면 $A\setminus X$도 그러하다..

이번에는 canonical projection $p:A\rightarrow A/R$와 $X\subseteq A$를 생각하자. §이항관계의 연산, ⁋명제 7에 의하여

\[p^{-1}(p(X))\supseteq X\]

를 얻는다. 일반적으로 반대방향 포함관계는 성립하지 않지만, 만일 $X$가 $R$-saturated라면 반대쪽 포함관계도 성립한다. 각각의 $x\in X$에 대하여, $p^{-1}(\left\{p(x)\right\})\subseteq X$이므로

\[p^{-1}(p(X))=\bigcup_{x\in X}p^{-1}(\left\{p(x)\right\})\subseteq X\]

가 성립하기 때문이다.

한편, $X$가 $R$-saturated가 아니더라도 집합 $p^{-1}(p(X))$는 $R$-saturated가 된다. 이를 보기 위해 $x\in p^{-1}(p(X))$를 임의로 택하고, $x\sim_{\tiny R} x’$를 만족하는 임의의 $x’$가 주어졌다 하자. 그럼

\[x\sim_{\tiny R} x'\iff p(x)=p(x')\]

이고, 주어진 가정으로부터 $p(x)\in p(X)$이므로 $x’\in p^{-1}(p(X))$를 얻는다. 한편, $X’$가 $X$를 포함하는 $R$-saturated subset이라면,

\[X'=p^{-1}(p(X'))\supseteq p^{-1}(p(X))\]

이므로 $p^{-1}(p(X))$는 $X$를 포함하는 $R$-saturated인 부분집합 중 가장 작은 것이다. 이를 $X$의 saturation이라 부른다.

Canonical decomposition

정의 6 동치관계 $(R,A,A)$와 $A$를 정의역으로 갖는 함수 $f$에 대하여, $f$가 $R$과 compatible하다는 것은 $x$에 대한 단항관계 $y=f(x)$가 $R$과 compatible하다는 것을 의미한다.

즉, $f$가 $R$과 compatible하려면 $f$는 각각의 equivalence class로 제한하였을 때 상수함수가 되어야 한다. 이제 §Retraction과 section, ⁋명제 4를 적용하면 다음을 얻는다.

명제 7 동치관계 $(R,A,A)$와 canonical $p:A\rightarrow A/R$을 생각하자. 그럼 $f:A\rightarrow B$가 $R$과 compatible한 것은 $f=h\circ p$이도록 하는 $h:A/R\rightarrow B$가 존재하는 것과 동치이다.

즉, 다음의 diagram이 commute한다.

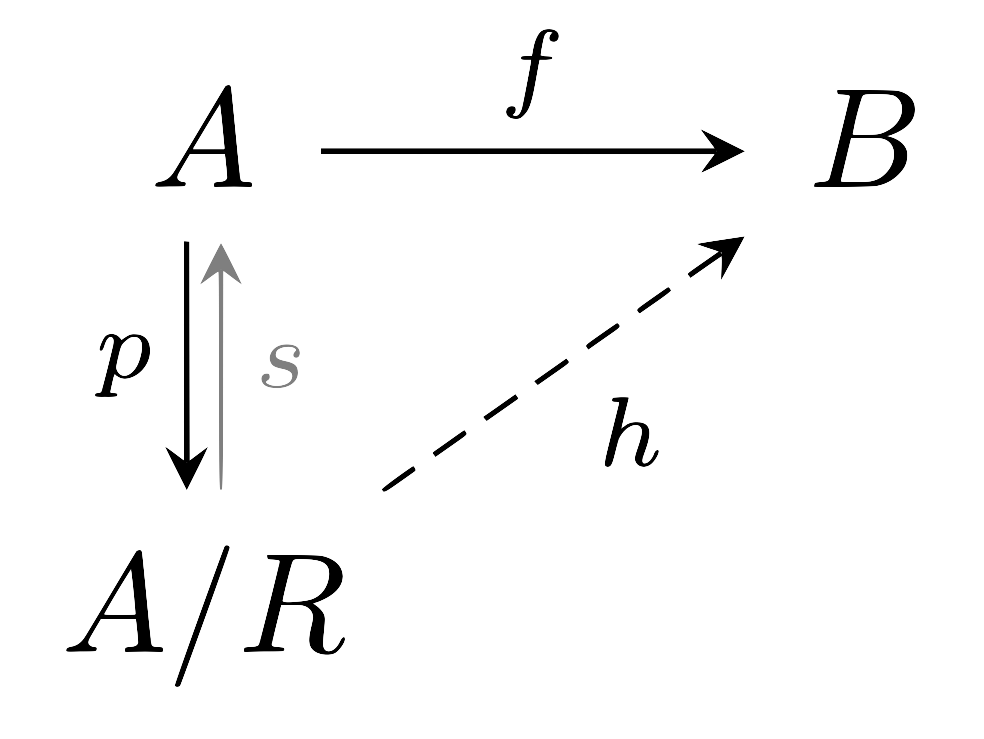
induced_injection

이 때 $h$는 $p$의 section $s$에 의하여 $h=f\circ s$로 유일하게 결정된다.

특별히 $R$이 $f$에 의해 정의된 동치관계라 하자. (정의 2) 그럼 다음의 diagram을 생각할 수 있다.

canonical_decomposition

이 때 $\tilde{f}$는 $f$의 공역 $F$를 $f(A)$로 제한하여 얻어지는 함수이고, $j$는 canonical injection이다. 위 그림의 commutativity로부터 식

\[f=j\circ\tilde{f}=j\circ h\circ p\]

를 얻는다. 만일 어떠한 $t, t’\in A/R$에 대해 $h(t)=h(t’)$라면, $x\in t$, $x’\in t’$에 대하여 $f(x)=f(x’)$이므로 $x\sim_{\tiny R}x’$이고, 따라서 $t=t’$가 되어 $h$는 단사함수이다. 그런데 $h$의 공역은 $f$의 치역으로 제한된 상태이므로, $h$는 전사함수이기도 하다. 따라서 $h$는 전단사이며, 위의 식을 $f$의 canonical decomposition이라 부른다.

추가로 공역 $B$에 동치관계 $S$가 주어졌다고 하자. 그럼 우선 다음의 diagram을 얻는다.

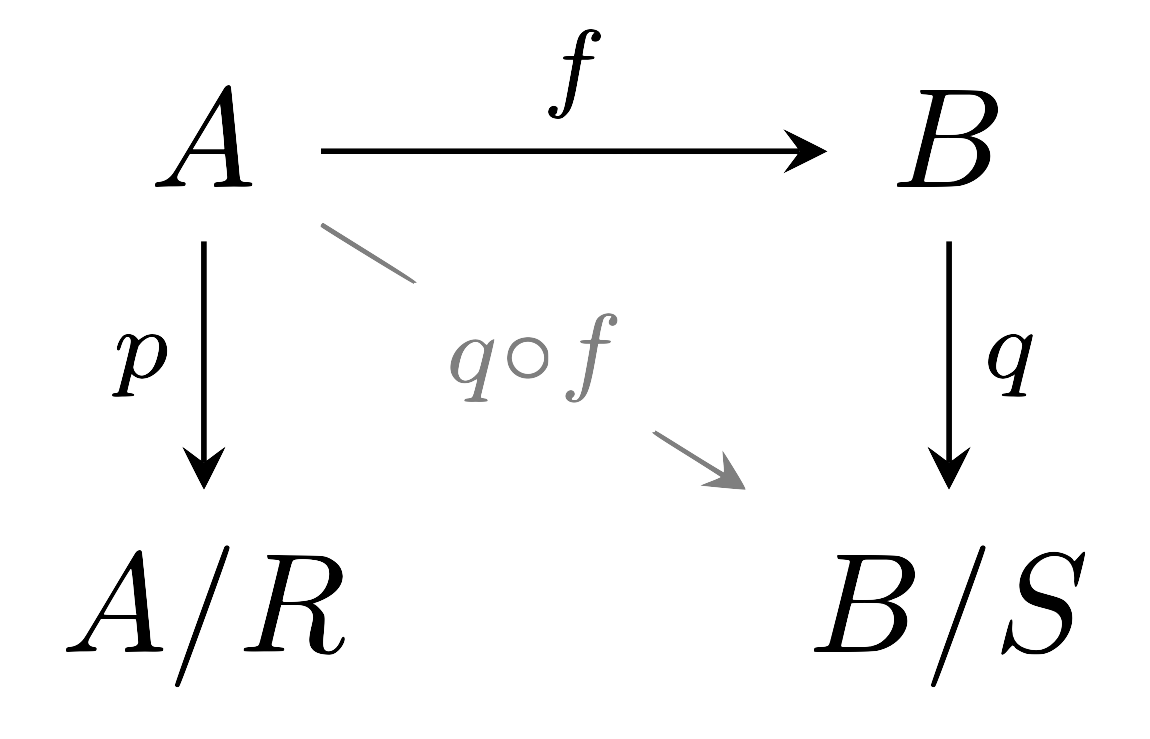
induced_mapping_of_equivalence

만일 $q\circ f$이 $R$과 compatible하다면, $f$가 $(R,S)$-compatible하다고 한다. 명제 7에 의해 이는 다시 $h:A/R\rightarrow B/S$가 존재하여 $h\circ p=q\circ f$인 것과 동치이다.

동치관계의 preimage

함수 $f:A\rightarrow B$가 주어졌다 하고, 동치관계 $(S,B,B)$와 canonical $p:B\rightarrow B/S$를 생각하자.

inverse_image_of_equivalence

그럼 자연스레 함수 $p\circ f:A\rightarrow B/S$가 정의되며, 이 함수가 정의 2를 통해 만드는 동치관계를 $f$에 의한 $S$의 preimage라 부른다.

동치관계의 quotient

다음 정의는 이미 §동치관계, ⁋예시 5에서 언급했던 것이다.

정의 8 집합 $A$ 위에 정의된 두 동치관계 $R,S$에 대해, $S$가 $R$보다 finer세밀하다하다는 것은 $x\sim_{\tiny S}y\implies x\sim_{\tiny R}y$가 항상 성립하는 것이다.

집합 $A$ 위에 정의된 두 동치관계 $R,S$가 주어졌고, $S$가 $R$보다 finer하다고 하자.

third_iso_1

그럼 함수 $p_S$가 전사함수이고, $p_S(x)=p_S(y)\implies p_R(x)=p_R(y)$가 항상 성립한다. 따라서 $p_R=h\circ p_S$이도록 하는 유일한 $h:A/S \rightarrow A/R$이 존재한다. (§Retraction과 section, ⁋명제 4) 이 때, $h$가 $A/S$ 위에 정의하는 $R$의 $S$에 의한 quotient라 부르고, $R/S$로 적는다. Canonical decomposition을 거치면

third_iso_2

와 같으며, 특히 $k$는 전단사함수이다.

동치관계의 곱

마지막으로 두 동치관계 $(R,A,A)$, $(R’,A’,A’$이 주어졌다고 하고, 관계 $(S, A\times A’, A\times A’)$를

$u\sim_{\tiny S}v$인 것은 어떠한 $x$, $x’$, $y$, $y’$가 존재하여 $u=(x,x’)$, $v=(y,y’)$이고 $x\sim_{\tiny R}y$, $x’\sim_{\tiny R’}y’$인 것이다

로 정의하자. $u=(x,x’),v=(y,y’),w=(z,z’)$이 $A\times A’$의 원소들이라 하면,

  • $u\sim_{\tiny S}u$가 항상 성립하는 것은 자명하다. $x\sim_{\tiny R}x$이고 $x’\sim_{\tiny R’}x’$이기 때문이다.
  • $u\sim_{\tiny S}v$라면 $x\sim_{\tiny R}y$이고 $x'\sim_{\tiny R'}y'$이므로 $y\sim_{\tiny R}x$이고 $y'\sim_{\tiny R'}x'$이고, 따라서 $v\sim_{\tiny S}u$이다.
  • $u\sim_{\tiny S}v$이고 $v\sim_{\tiny S}$라 하자. 그럼 $x\sim_{\tiny R}y,x'\sim_{\tiny R'}y',y\sim_{\tiny R}z,y'\sim_{\tiny R'}z'$가 각각 성립한다. 이제 $x\sim_{\tiny R}y$와 $y\sim_{\tiny R}z$로부터 $x\sim_{\tiny R}z$이고, $x’\sim_{\tiny R’}y’$와 $y’\sim_{\tiny R’}z’$로부터 $x’\sim_{\tiny R’}z’$이다. 즉 $u\sim_{\tiny S}w$가 성립한다.

따라서 $S$는 동치관계가 된다. 이 동치관계를 $R$과 $R’$의 곱product이라 부르고 $R\times R’$로 적는다.

두 함수 $f:A\rightarrow B$, $f’:A’\rightarrow B’$가 주어졌다고 하고, $R$과 $R’$을 각각 $f$와 $f’$에 의해 유도되는 동치관계라 하자. 그럼 $f\times f’:A\times A’\rightarrow B\times B’$가 잘 정의되고, 이 함수를 통해 $A\times A’$ 위에 동치관계를 정의할 수 있다. 이 동치관계를 잠시 $S$라 하면, 임의의 $u=(x,x’),v=(y,y’)\in A\times A’$에 대해

\[\begin{aligned}u\sim_{\tiny S}v&\iff (f\times f')(u)=(f\times f')(v)\iff (f(x),f'(x')=(f(y),f'(y'))\\ &\iff (f(x)=f(y))\wedge(f'(x')=f'(y'))\iff (x\sim_{\tiny R}y)\wedge(x'\sim_{\tiny R'}y')\\&\iff u\sim_{\tiny R\times R'}v\end{aligned}\]

이므로 $S=R\times R’$이다. 이 때 $f\times f’$에 의한 $A\times A’$의 image는 $f(A)\times f’(A’)$와 같으므로, $f\times f’$의 canonical decomposition을 생각하면 $(A\times A’)/(R\times R’)$과 $f(A)\times f’(A’)$ 사이의 전단사함수가 존재한다.

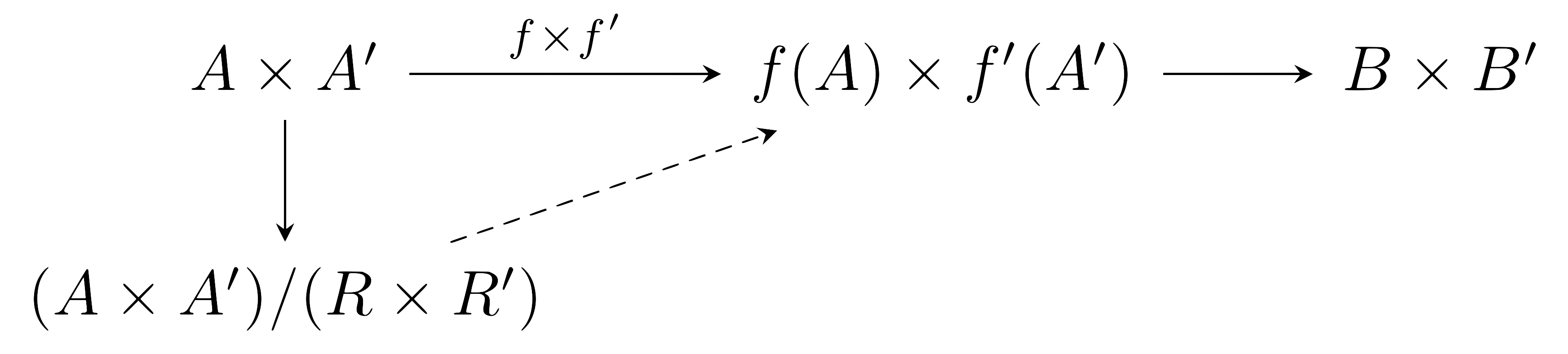
canonical_bijection_between_product

한편 다음의 diagram을 생각하자.

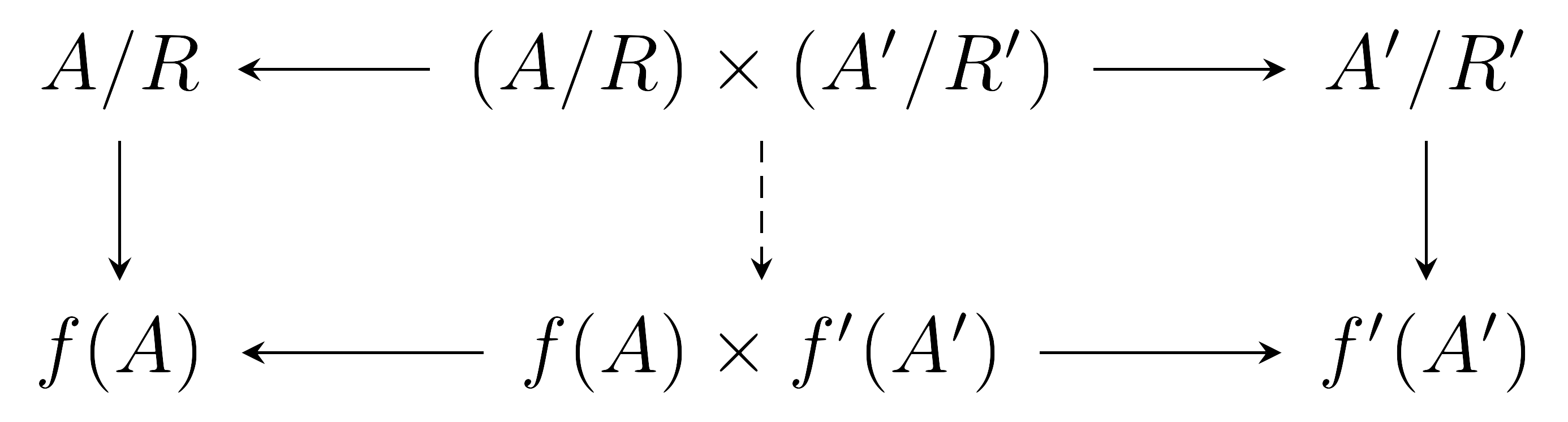
canonical_bijection_between_product_2

여기서 $A/R\rightarrow f(A)$와 $A’/R’\rightarrow f’(A’)$는 각각 $f$와 $f’$의 canonical decomposition들로부터 얻어지는 전단사함수이다. 따라서 이들에 의해 유도되는 함수 $(A/R)\times (A/R’)\rightarrow f(A)\times f’(A’)$ 또한 전단사함수이다.

위에서 얻어진 두 개의 전단사함수와 그 역들을 적절히 합성해주면 $(A\times A’)/(R\times R’)$과 $(A/R)\times(A’/R’)$ 사이의 전단사함수를 얻을 수 있다. 이 전단사함수들 또한 canonical이라 부른다.

참고문헌

[Bou] N. Bourbaki, Theory of Sets. Elements of mathematics. Springer Berlin-Heidelberg, 2013.

댓글남기기