K

Grad. student in mathematics

Abelian group에서와는 다르게, 앞선 글에서 정의한 weak direct product는 일반적인 group에서 universal property를 만족하지 않는다.

예시 1 임의의 nonabelian group $G$를 생각하고, $a,b\in G$에 대해 $ab\neq ba$가 성립한다 하자. Group homomorphism $f_1, f_2: (\mathbb{Z},+)\rightarrow (G,\cdot)$을

\[f_1(1)=a, \qquad f_2(1)=b\]

을 통해 정의하자. Index set $I=\{1,2\}$가 유한집합이므로 $(\mathbb{Z},+)$ 두 개의 weak direct product는 $\mathbb{Z}\times\mathbb{Z}$와 같다.

그러나 우리는 다음의 diagram

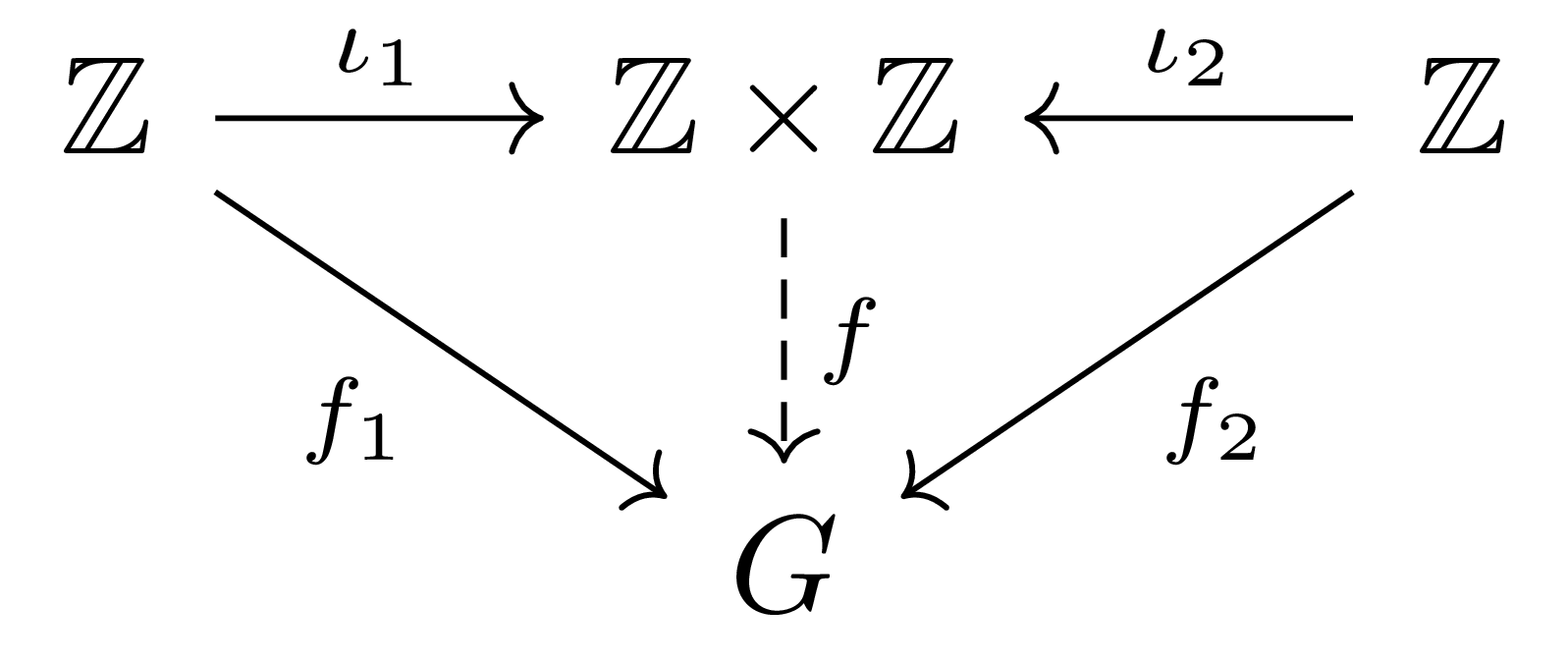
counterexample

을 commute하게 만드는 $f:\mathbb{Z}\times\mathbb{Z}\rightarrow G$는 존재하지 않음을 알 수 있다. 만일 그러한 $f$가 존재한다면

\[\begin{aligned}ab&=f_1(1)f_2(1)=f(\iota_1(1))f(\iota_2(1))=f(\iota_1(1)+\iota_2(1))\\ &=f(\iota_2(1)+\iota_1(1))=f(\iota_2(1))f(\iota_1(1))=f_2(1)f_1(1)\\ &=ba\end{aligned}\]

가 되어 $a,b$의 선택에 모순이기 때문이다.

그러므로 일반적인 group들 사이에서 direct sum과 같이, universal property를 만족하는 대상을 찾기 위해서는 새로운 방법을 도입해야 한다. 이를 위해서는 우선 free group을 먼저 정의해야 한다.

Free group

임의의 group $G$는 적당한 집합 위에 이항연산과 항등원, 역원의 개념을 추가한 것으로 생각할 수 있다. 뿐만 아니라, 임의의 group homomorphism은 자연스럽게 집합들 사이의 함수로 볼 수도 있다. 즉, forgetful functor $U: \Grp \rightarrow\Set$이 존재한다. 이 섹션에서 우리는 $U$의 left adjoint $F:\Set \rightarrow\Grp$을 정의한다. Left adjoint functor의 정의에 의해, 이는 다음의 natural isomorphism

\[\Hom_\Set(X, U(G))\cong\Hom_\Grp(F(X), G)\]

을 만족하는 functor이다. ([범주론] §수반함자, ⁋정의 1) 즉 functor $F$는 임의의 집합 $X$와 임의의 group $G$에 대하여, $f\in\Hom_\Set(X, U(G))$마다 $\Hom_\Grp(F(X),G)$의 원소를 유일하게 대응시키는 bijection으로 주어진다. 이를 다시 쓰면 다음과 같다.

정의 2 공집합이 아닌 집합 $X$에 대하여, $X$에 의해 정의된 free group자유군 $F(X)$는 다음과 같은 universal mapping problem의 solution $(F(X), \eta_X\in\Hom_\Set(X,UF(X)))$으로 정해진다.

임의의 group $G$에 대하여, 만일 어떤 함수 $f:X\rightarrow U(G)$가 주어졌다면 유일한 group homomorphism $\hat{f}:F(X)\rightarrow G$가 존재하여 $U(\hat{f})\circ\eta_X=f$를 만족한다.

여기에서 $\eta_X$는 adjunction $F\dashv U$의 unit에 불과하다. 물론 이를 위해서는 $F(X)$를 실제로 만들어내야 한다.

대략적인 흐름을 소개한다. 우선 $X$와 disjoint하며 같은 cardinality를 갖는 집합 $X^{-1}$을 생각하자. $X^{-1}$은 어떤 특별한 집합이 될 이유는 없지만, 우리는 bijection $X\rightarrow X^{-1}$ 하나를 골라 $x\in X$의 $X^{-1}$에서의 image를 $x^{-1}$으로 표기할 것이다. 또, $X\cup X^{-1}$과 disjoint한 한원소집합을 하나 골라 이 집합의 원소를 $e$라 하자.

그럼 group $F$의 원소는 집합 $X\cup X^{-1}\cup \{e\}$에 의해 정의되는 reduced word들의 모임이다. 여기서 word라는 것은 그저 집합 $X\cup X^{-1}\cup \{e\}$의 원소들의 나열인데, 만일 $xx$와 같이 같은 원소가 두 번 연달아 나열되거나, $xx^{-1}$과 같이 $x$ 직후에 $x^{-1}$이 나열되거나, $xey$와 같이 두 개의 항 사이에 $e$가 있을 경우 이들을 각각 $x^2$, $e$, $xy$으로 줄여 쓸 수 있다. 하지만, 예를 들어 $y\neq x^{-1}$이라면 $xyx$를 줄여 쓸 방법은 없다. 이렇게 줄여 쓴 word를 reduced word라 부른다.

우리는 모든 word를 reduced word로 줄여 쓸 수 있다.1 이들 사이의 연산과 항등원을 정의하자. 항등원은 당연히 reduced word $e$이다. 연산은 그냥 두 개의 word를 이어쓴 후, 이를 reduced word로 줄여 쓴 것으로 정의된다. 예를 들어 word $x_1x_2$와 $x_3x_4$의 연산은 $x_1x_2x_3x_4$로 주어진다. 그럼 $e$는 이 연산 하에서의 empty word로 볼 수도 있다. 이 연산은 자명하게 associative하다. 역원은 원래 주어진 원소의 각 항들의 역원 취한 후, 이를 거꾸로 나열한 것이다. 예를 들어 다음의 word

\[x_1x_2^{-1}x_3^2\]

의 역원은

\[x_3^{-2}x_2x_1^{-1}\]

이 되며, 실제로 이들 둘을 연산해보면 $e$가 됨을 확인할 수 있다.

이제 우리는 group $F$를 만들었으며, 여기서 $X$의 원소로 이루어진 길이 1짜리 원소들을 $X$의 원소와 동일시하면 $\iota:X\rightarrow F$ 또한 얻는다. 그럼 이들이 정의 2의 universal property를 만족한다는 것을 쉽게 보일 수 있다. 이를 위해서는 $\bar{f}$를 $F$에 등장하는 원소들 $x\in X$들을 모두 $g(x)$로 바꿔주는 함수로 정의한 후, 이것이 group homomorphism이 된다는 것을 확인하면 된다.

따름정리 3 임의의 group $G$는 free group의 homomorphic image이다.

증명

$G$의 generator들의 모임 $X$를 생각한 후, $X$에 대한 free group $F$를 생각하자. 함수 $X\hookrightarrow G$에 의해 정의되는 $F$에서 $G$로의 group homomorphism이 존재하며, 이 homomorphism의 image는 $G$의 generator들을 모두 포함하므로 surjective하다.

Free product

위의 아이디어를 응용하면 비슷하게 free product 또한 정의할 수 있으며, 이는 우리가 찾아헤매던 coproduct가 된다. 마찬가지로 construction은 간략하게만 소개한다.

Group들의 family $(G_i)$가 주어졌다 하자. 편의를 위해 이들이 모두 서로 disjoint하다고 하고, $X=\coprod G_i$라 하자. 즉, 임의의 원소 $x\in X$에 대하여 $x\in G_i$인 $i$를 유일하게 찾을 수 있다. $G_i$들은 이미 역원을 포함하고 있으므로, generator들의 모임으로는 $X\cup\{e\}$만 생각하면 충분하다.

$(G_i)$들의 free product $\prod^\ast G_i$는 이 집합 $X\cup\{e\}$에서 만들어지는 reduced word들의 모임이다. 큰 흐름은 free group을 정의할 때와 같지만, 이번에는 $G_i$의 원소들이 자신들끼리 연산이 가능하므로 reduced word를 정의할 때 조금 더 신경을 써 주어야 한다. Free product를 정의할 때 사용하는 reduced word라는 말은 집합 $X\cup\{e\}$의 원소들로 만들어진 word

\[x_1x_2\cdots x_n\]

가 다음의 세 조건을 만족한다는 것을 의미한다.

  1. 만일 $n>1$이라면 $x_k$들 가운데 어떤 것도 $e$와 같지 않다.
  2. 만일 $x_k\in X$라면 $x_k$는 이 원소가 포함된 group $G_i$에서 항등원이 아니다.
  3. 인접한 두 원소 $x_i, x_{i+1}$은 반드시 서로 다른 group에 속한다.

임의의 word가 주어졌을 때, 이를 reduced word로 만드는 법은 간단하다. 인접한 원소들이 서로 같은 group에 속하는 원소인지를 모두 체크해본 후, 같은 group에 속하는 원소들은 이 group에서의 연산을 통해 하나의 원소로 합쳐준다. 이 과정에서 (혹은 원래부터) 어떤 group에서의 항등원이 나왔다면, 그 원소는 지워버리면 된다.

그럼 $\prod^\ast G_i$ 위의 연산은 free group을 정의할 때와 동일하게 이어쓰기연산이며, 어렵지 않게 이 모임이 group structure를 갖는다는 것을 확인할 수 있다. 또, 예시 1과 같은 상황은 더 이상 일어나지 않는데, 이는 두 group $G_1,G_2$가 abelian이라 하더라도 그 free product $G_1\ast G_2$는 더 이상 abelian group이 아니기 때문이다.

예시 4 예시 1과 동일한 상황을 생각하자. 대신 표기상의 편의를 위해 $G_1=\langle a\rangle\cong\mathbb{Z}$, $G_2=\langle b\rangle\cong\mathbb{Z}$이라 하자. 그럼 $G_1\ast G_2$의 원소는 다음과 같은 원소들

\[ab, a^2b, a^{-1}ba^3, bab^2, \cdots\]

의 모임이다. 예를 들어, 두 개의 원소 $a^2b$와 $bab^2$를 연산하면 우리는

\[(a^2b)(bab^2)=a^2bbab^2=a^2b^2ab^2\]

을 얻는다.

이 때 $\langle a\rangle$과 $\langle b\rangle$은 $G_1\ast G_2$의 cyclic subgroup이고, 따라서 $G_1$과 $G_2$에서 $G_1\ast G_2$으로의 homomorphism을 $a\mapsto a$, $b\mapsto b$로 정의하면 자연스러운 inclusion map $\iota_1$과 $\iota_2$를 얻는다.

물론 예시 1과 같은 문제 또한 일어나지 않는다. $\iota_1(a)\iota_2(b)=ab$이고 $\iota_2(b)\iota_1(a)=ba$인데, 이 두 원소는 $\prod^\ast G_i$의 서로 다른 원소이기 때문이다.

명제 5 Free product $\prod^\ast G_i$는 $\Grp$에서의 coproduct이다.

증명

임의의 group $H$와 group homomorphism들 $f_i:G_i\rightarrow H$가 주어졌다 하자. 그럼 $X=\coprod U(G_i)$의 universal property에 의하여, inclusion map $\iota_i:U(G_i)\rightarrow X$들에 대해 $U(f_i)=f\circ \iota_i$를 만족하는 유일한 함수 $f:X\rightarrow U(H)$가 존재한다. 이제 free product의 universal property (정의 2)로부터 group homomorphism $\hat{f}:F(X)\rightarrow H$를 얻으며, 이 때 $f_i$들이 group homomorphism이었다는 사실을 사용하면 $f$가 위의 reduction 과정을 통해 factor하며, 따라서 $\prod^\ast G_i\rightarrow H$를 정의한다는 것을 안다.

한편 임의의 group $G$에 대하여, group homomorphism $\mathbb{Z}\rightarrow G$는 $1\in \mathbb{Z}$가 $G$의 어떠한 원소로 옮겨지는지에 의해 유일하게 결정된다. 즉 다음 isomorphism

\[\Hom_\Grp(\mathbb{Z},G)\cong U(G)\]

가 존재하며, [범주론] §표현가능한 함자, 예시 2와 비슷한 논증으로 위의 isomorphism이 $U$의 representation임을 알 수 있으며, 뿐만 아니라

\[\Hom_\Grp(\mathbb{Z},G)\cong \Hom_\Set(\ast, U(G))\]

으로 생각하면 $\mathbb{Z}=F(\ast)$인 것으로 해석할 수 있다. 따라서 임의의 집합 $X$에 대하여 [범주론] §수반함자, ⁋정리 9를 이용하면 free group $F(X)$를 $\mathbb{Z}$들의 free product

\[F(X)=F\left(\coprod_{x\in X} \{x\}\right)\cong \coprod_{x\in X} F(\ast)={\prod_{x\in X}}^\ast \mathbb{Z}\]

으로 나타낼 수 있다.

참고문헌

[Bou] Bourbaki, N. Algebra I. Elements of Mathematics. Springer. 1998.

  1. Word들 사이의 연산을 정의해주기 위해 reduced word를 꼭 도입해줘야 하는 것은 아니지만, 표현의 유일성을 위해 reduced word를 도입해주는 것이 좋다. ↩

댓글남기기