군들의 곱
우리는 임의의 category $\mathcal{A}$에서 product를 정의하는 방법을 알고 있다. ([범주론] §극한, ⁋예시 6) 다음 보조정리는 category $\Grp$의 임의의 product가 항상 존재한다는 것을 보여준다.
보조정리 1 $\Grp$은 cartesian monoidal category이다.
증명
우선 $\Set$에서 product의 universal property을 만족하는 곱집합 $\prod_{i\in I} G_i$는 이미 [집합론] §집합의 곱, ⁋정의 1에서 정의했다. 표기상의 편의를 위해 $\prod_{i\in I}G_i$의 원소 $f:I\rightarrow \bigcup G_i$를 순서쌍 $(a_i)_{i\in I}$으로 표기하기로 한다.
이제 집합 $\prod_{i\in I}G_i$의 임의의 두 원소 $x=(x_i)_{i\in I},y=(y_i)_{i\in I}$에 대하여,
\[xy=(x_i)_{i\in I}(y_i)_{i\in I}=(x_iy_i)_{i\in I}\]으로 정의하자. 그럼 $\prod_{i\in I}G_i$는 이 연산에 대해 group의 구조를 가지며, 항등원은 $(e_i)_{i\in I}$이고 $x=(x_i)_{i\in I}$의 역원은 $(x_i^{-1})_{i\in I}$인 것을 알 수 있다. 또, 임의의 $j\in I$에 대하여
\[\pr_j(xy)=\pr_j(x_iy_i)_{i\in I}=x_jy_j=\pr_j(x)\pr_j(y)\]이므로 $\pr_j$가 group homomorphism이다.
이제 이렇게 정의한 $(G=\prod_{i\in I}G_i,(\pr_i)_{i\in I})$가 universal property를 만족하는 것을 증명하자. 이를 위해서는 곱집합의 universal property로 얻어지는 함수 $f:H\rightarrow G$가 group homomorphism이라는 것만 보이면 충분하다. 이제 임의의 $x,y\in H$와 임의의 $i\in I$에 대하여,
\[f(xy)=(f_i(xy))_{i\in I}=(f_i(x)f_i(y))_{i\in I}=(f_i(x))_{i\in I}(f_i(y))_{i\in I}=f(x)f(y)\]이므로 $f$는 group homomorphism이 되고 따라서 위의 $(G=\prod_{i\in I}G_i,(\pr_i)_{i\in I})$가 universal property를 만족한다.
다음 따름정리들 또한 product의 universal property에 의해 자명하다.
따름정리 2 Group들의 family $(G_i)$에 대하여, 이들 family의 product는 유일한 isomorphism에 대해 유일하게 결정된다.
증명
임의의 category의 terminal object는 유일한 isomorphism에 대하여 유일하게 결정된다.
따름정리 3 $(G_i)$, $(H_i)$가 동일한 집합 $I$를 index set으로 갖는 group들의 family이고, 각각의 $i$마다 group homomorphism $f_i:G_i\rightarrow H_i$가 주어졌다 하자. 그럼 다음의 diagram
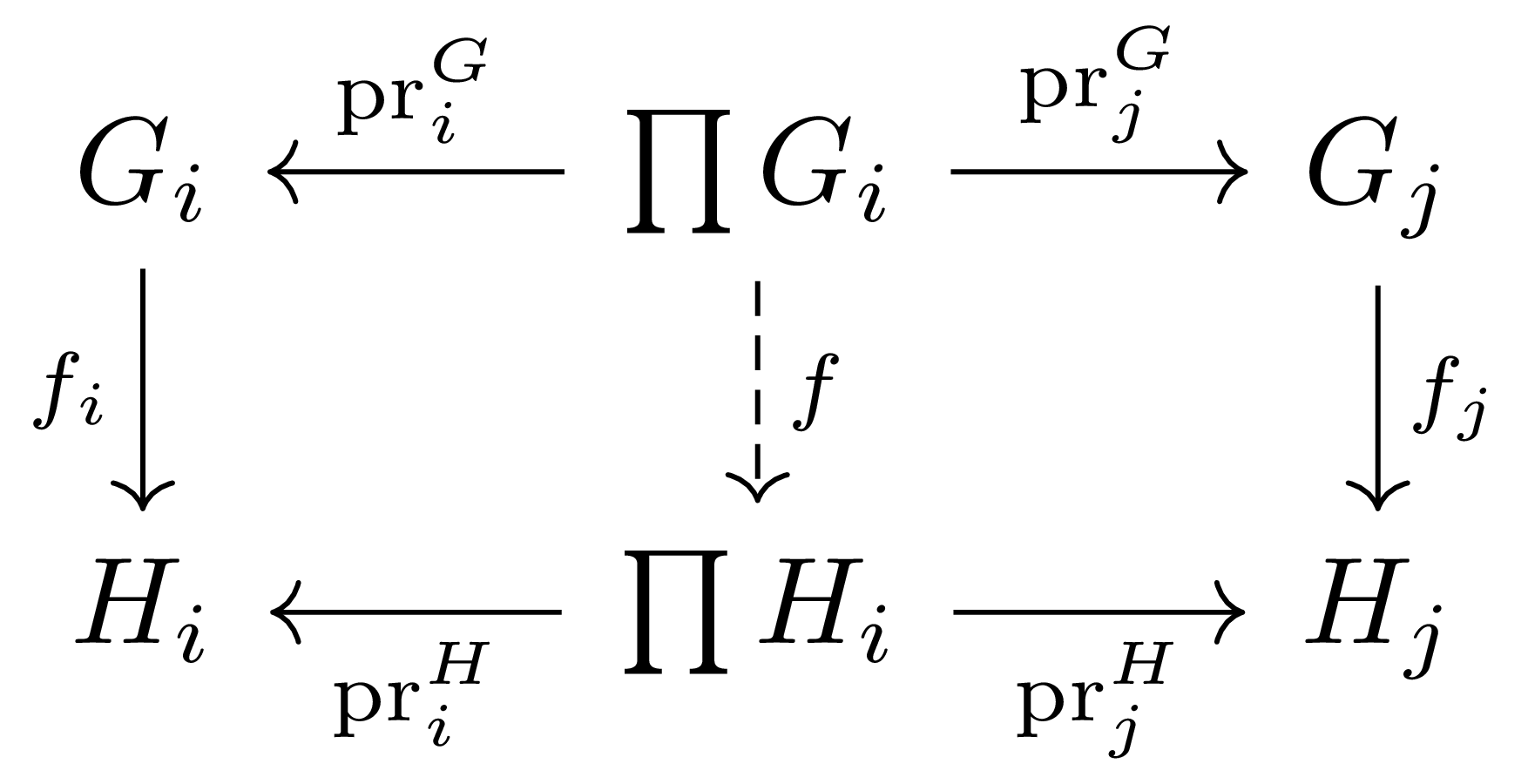
을 commute하도록 하는 유일한 group homomorphism $f:\prod G_i\rightarrow\prod H_i$이 존재한다. 이 때 $\ker f=\prod\ker f_i$이고, $\im f=\prod\im f_i$이다.
증명
$\prod H_i$는 주어진 조건을 만족하는 cone들의 모임의 terminal object이다. ([범주론] §극한, §§극한의 보편성질) 이렇게 정의되는 commutative diagram에 의하여
\[x\in\ker f\iff f(x)=e\iff \forall i(\pr_i^H(f(x))=e_i)\iff \forall i((f_i\circ \pr_i^G)(x)=e_i)\iff \forall i(\pr_i^G(x)\in\ker f_i)\]이므로 $\ker f=\prod\ker f_i$가 성립한다.
이와 유사하게, $y\in\prod H_i$에 대해 $y\in\im f$인 것은 $y=f(x)$인 $x\in H_i$가 존재하는 것과 동치이고, 이러한 $x$에 대하여
\[\pr_i^H(y)=\pr_i^H(f(x))=f_i(\pr_i^G(x))\in\im f_i\]이므로 $\im f=\prod\im f_i$ 또한 성립한다.
따름정리 4 Group들의 family $(G_i)_{i\in I}$가 주어졌다 하자. 각각의 $i\in I$에 대하여 $H_i$들이 $G_i$의 normal subgroup이라면, $\prod H_i$도 $\prod G_i$의 normal subgroup이고 그 quotient group은 $\prod (G_i/H_i)$와 같다.
증명
Canonical homomorphism들 $p_i:G_i\rightarrow G_i/H_i$들에 따름정리 3를 적용하면 된다.
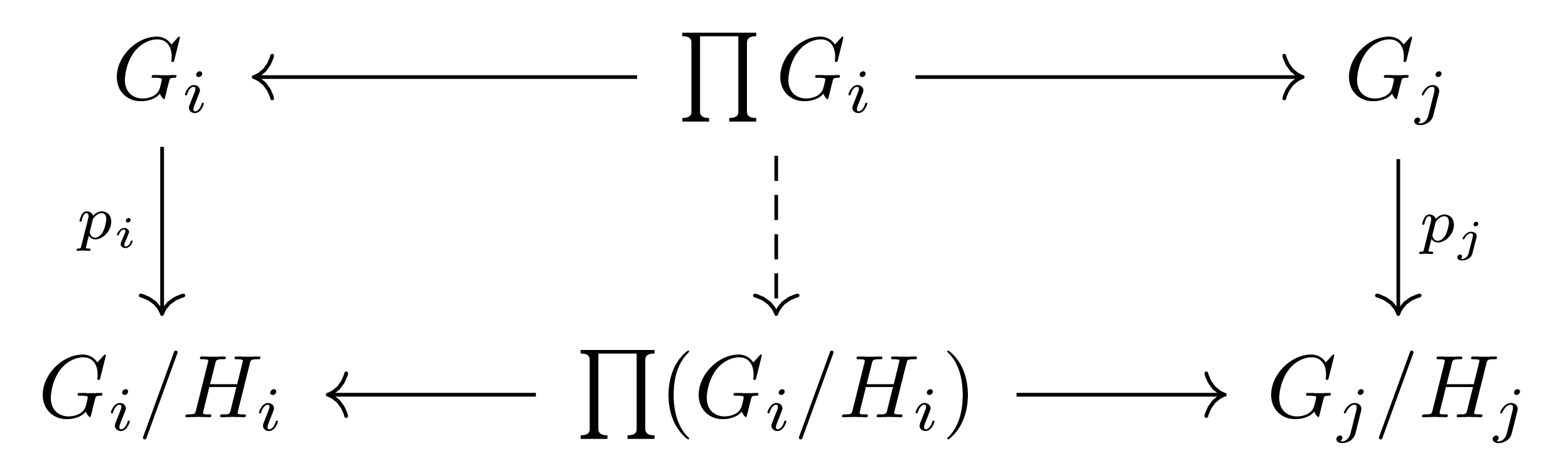
$p_i\circ\pr_i$들 각각은 전사인 homomorphism들의 합성이므로 전사이고 따라서 앞선 따름정리에 의해 $\im p$는 $\prod(G_i/H_i)$와 같다. 또, $p_i$들 각각의 kernel은 $H_i$와 같다. 따라서 first isomorphism theorem에 의하여
\[\biggl(\prod_{i\in I} G_i\biggr)\bigg/\biggl(\prod_{i\in I}H_i\biggr)\cong\prod_{i\in I} (G_i/H_i)\]가 성립한다.
물론, $H_i$들이 $G_i$들의 normal이 아닌 subgroup이더라도 $\prod H_i$는 $\prod G_i$의 subgroup이 된다.
따름정리 5 Group들의 family $(G_i)_{i\in I}$가 주어졌다 하자. 만일 각각의 $i\in I$에 대하여 $H_i\leq G_i$라면, $\prod H_i$는 $\prod G_i$의 subgroup이다.
증명
Inclusion homomorphism들 $\iota_i:H_i\hookrightarrow G_i$에 따름정리 3를 적용하면, $\iota$는 단사이고 $\prod H_i$는 정확히 $\iota$의 image이므로 $\prod G_i$의 subgroup이다.
부분곱
위의 따름정리들은 다음의 상황에서 특히 유용하다.
$(G_i)_{i\in I}$가 group들의 family라 하고, $I$의 부분집합 $J$를 생각하자. 그럼 product $\prod_{j\in J}G_j$가 잘 정의된다. 한편, 다음의 식
\[G_i'=\begin{cases} G_i&i\in J\\ \{e\}&i\not\in J\end{cases}\]으로 정의된 group들의 family $(G_i’)$, 그리고 $G_i’$에서 $G_i$로의 group homomorphism들
\[f_i=\begin{cases} \id_{G_i}&i\in J\\ \iota_i&i\not\in J\end{cases}\]을 생각하자. 그럼 어렵지 않게 $\prod_{i\in I}G_i’\cong\prod_{j\in J}G_j$임을 보일 수 있으며, 따라서 따름정리 4에 의하여 다음의 식
\[\biggl(\prod_{i\in I}G_i\biggr)\bigg/\biggl(\prod_{j\in J}G_j\biggr)\cong\prod_{i\in I\setminus J} G_i\]이 성립함을 확인할 수 있다.
참고문헌
[Bou] Bourbaki, N. Algebra I. Elements of Mathematics. Springer. 1998.

댓글남기기