이번 글에서는 ring homomorphism \(\phi:A \rightarrow B\)를 통해 \(A\)-module을 \(B\)-module로, 혹은 \(B\)-module을 \(A\)-module로 바꾸는 방법에 대해 살펴본다. 따라서, 기존과 같이 스칼라곱 및 연산을 줄여쓰면 혼동의 여지가 있으므로, multiplication map들은 기존과 같이 \(\cdot\)을 생략하고 action들을 \(\cdot\) (혹은 \(\cdot_A\)와 \(\cdot_B\))으로 표기하기로 한다.
Restriction of scalar
\(B\)-module \(\rho_N:B\otimes N \rightarrow N\)이 주어졌다 하자. 그럼 다음 합성
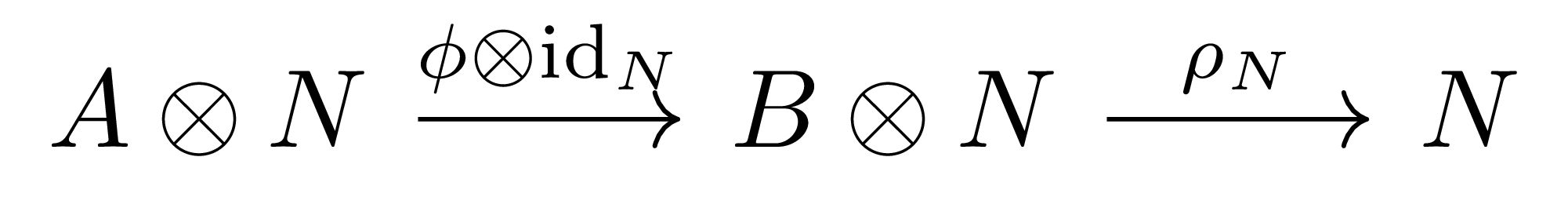
을 생각하면, \(\phi^\ast\rho_N:A\otimes N \rightarrow N\)은 action이 만족해야 하는 모든 조건들을 만족하고 따라서 \(N\) 위에 \(A\)-module 구조를 정의한다. 뿐만 아니라, 다음의 diagram
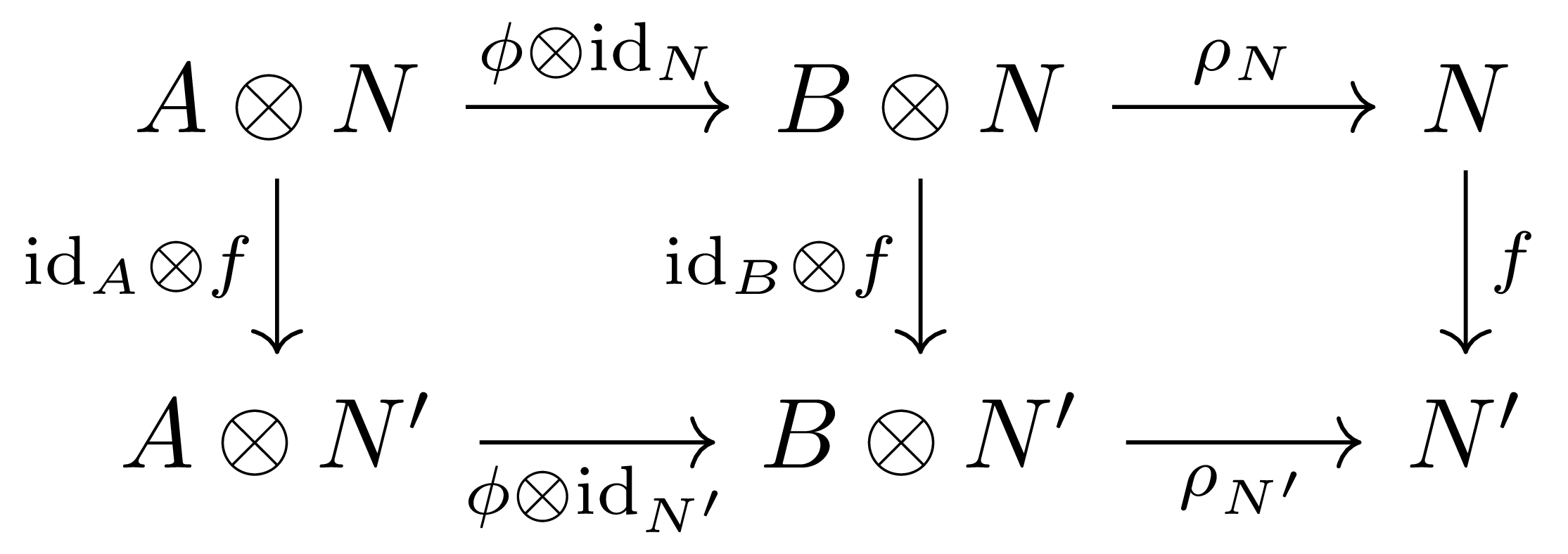
을 생각하면 우리는 이렇게 \(A\)-module을 대응시키는 것이 functorial하다는 것을 안다.
정의 1 Ring homomorphism \(\phi:A \rightarrow B\)에 대하여, 위와 같은 방식으로 정의된 functor를 \(\phi^\ast: \lMod{B} \rightarrow \lMod{A}\)로 쓰고, restriction of scalar스칼라의 제한이라 부른다.
즉 이는 그냥 임의의 \(B\)-module \(\rho_N: B\otimes N \rightarrow N\)이 주어졌을 때, 이를 이용하여 \(N\) 위에 \(A\)의 action을 다음 식
\[\alpha\cdot_A y:=\phi(\alpha)\cdot_B y\]으로 정의하는 것이다.
특별히 \(N=B\)인 경우를 생각하자. 집합으로서는 \(\phi^\ast B\)와 \(B\)가 동일하므로, 기존의 ring homomorphism \(\phi:A \rightarrow B\)와 \(\phi^\ast B\)의 action 사이의 관계를 확인할 수 있는데, 이 경우 \(\phi\)는 \(A\)-linear map이 되는 것을 확인할 수 있다.
예시 2 Forgetful functor \(U: \lMod{B} \rightarrow\Ab\)는 (유일한) ring homomorphism \(\mathbb{Z}\rightarrow B\)로부터 유도되는 것이다.
Extension of scalar
이제 우리는 \(\lMod{A}\)에서 \(\lMod{B}\)로 가는 두 개의 functor를 정의할 것이다. 편의상 \(A\)-module \(M\)을 고정하자.
두 \(A\)-module \(\phi^\ast B\)와 \(M\)의 tensor product \(\phi^\ast B\otimes_AM\)을 생각하자. 그럼 이 위에 다음의 식
\[\beta'\cdot_B(\beta\otimes_A x)=(\beta'\beta)\otimes_A x\]을 통해 \(B\)의 action \(\cdot_B\)를 정의할 수 있다. 이것이 실제로 action이 된다는 것은 단순계산을 통해서도 어렵지 않게 얻어지며, 혹은 합성
\[B\otimes_\mathbb{Z}(\phi^\ast B\otimes_AM)\cong (B\otimes_\mathbb{Z}\phi^\ast B)\otimes_AM \overset{\mu_B}{\longrightarrow} \phi^\ast B\otimes_AM\]으로 얻어지는 것으로 생각할 수도 있다.1 또, 임의의 \(A\)-linear map \(u:M \rightarrow M'\)에 대하여 \(\id_{\phi^\ast B}\otimes_A u\)가 이렇게 정의된 두 \(B\)-module 사이의 \(B\)-linear map을 정의하는 것을 확인할 수 있다.
정의 3 위의 functor \(\phi^\ast B\otimes_A-:\lMod{A} \rightarrow \lMod{B}\)를 간단히 \(\phi_!\)라 쓰고, 이를 extension of scalar스칼라의 확장이라 부른다.
Coextension of scalar
이전과 마찬가지로 \(A\)-module \(M\)을 고정하자. 이번에는 두 \(A\)-module \(\phi^\ast B\)와 \(M\) 사이의 homomorphism을 생각한다. 다음 abelian group
\[\Hom_A(\phi^\ast B,M)\]위에 \(B\)-module 구조를 다음의
\[\beta\cdot g: (\beta'\mapsto g(\beta'\beta))\]으로 정의하자. 임의의 \(\alpha\in A\)와 임의의 \(\beta'\in \phi^\ast B\)에 대하여
\[(\beta\cdot g)(\alpha\cdot \beta')=g(\phi(\alpha)\beta'\beta)=g(\alpha\cdot(\beta'\beta))=\alpha\cdot g(\beta'\beta)=\alpha\cdot (\beta\cdot g)(\beta')\]이므로 \(\beta\cdot g\) 또한 \(A\)-linear map이다. 약간의 계산을 통해 이 또한 functorial하다는 것을 확인할 수 있으며, 따라서 다음이 정의된다.
정의 4 Functor \(\Hom_A(\phi^\ast B,-): \lMod{A} \rightarrow \lMod{B}\)를 coextension of scalar스칼라의 쌍대확장이라 부르고 \(\phi_\ast\)로 적는다.
수반함자
위에서 정의한 세 functor들 사이에는 특정한 adjoint 관계들이 있다. 우선 다음 보조정리를 보이자.
보조정리 5 Right \(B\)-module \(N_1\), left \(B\)-module \(N_2\)에 대하여, 두 abelian group \(\phi^\ast N_1\otimes_A \phi^\ast N_2\)와 \(N_1\otimes_B N_2\)를 생각하자. 그럼 이들 사이의 유일한 bilinear map \(\Phi:\phi^\ast N_1\otimes_A \phi^\ast N_2 \rightarrow N_1\otimes_BN_2\)가 존재하여, 임의의 \(y_1\otimes_A y_2\in \phi^\ast N_1\otimes_A\phi^\ast N_2\)가 \(y_1\otimes_B y_2\in N_1\otimes_BN_2\)로 옮겨지도록 할 수 있다.
만일 \(A\)가 commutative ring이었다면, \(\Phi\)는 \(A\)-linear map \(\phi^\ast N_1\otimes_A\phi^\ast N_2 \rightarrow\phi^\ast(N_1\otimes_BN_2)\)이 된다.
증명
\(\phi^\ast N_1\times\phi^\ast N_2\)에서 \(N_1\otimes_B N_2\)로의 함수를 \((y_1,y_2)\mapsto y_1\otimes_B y_2\)로 정의한 후, 이것이 \(A\)의 스칼라곱에 대해서도 잘 행동하는 것을 보이면 된다. 그런데 \(\phi^\ast N_1,\phi^\ast N_2\) 위에서 \(A\)의 스칼라곱은 \(\phi(\alpha)\)를 통한 \(B\)-action으로 정의되므로, 임의의 \(\alpha\in A\)에 대하여
\[(\alpha\cdot_A y_1,y_2)=(\phi(\alpha)\cdot_B y_1, y_2)\mapsto (\phi(\alpha)\cdot_B y_1)\otimes_B y_2=y_1\otimes_B(\phi(\alpha)\cdot_B y_1)\]가 성립하며, 따라서 \((\alpha\cdot_A y_1,y_2)\)와 \(y_1,\alpha\cdot_Ay_2\)가 같은 원소로 보내지므로 tensor product의 universal property에 의해 증명이 완료된다.
다음 명제들은 일반적인 경우에서도 증명할 수 있지만, 편의를 위해 \(A, B\)가 모두 commutative ring이라 가정한다.
명제 5 Adjoint \(\phi_!\dashv\phi^\ast\)가 존재한다.
증명
임의의 \(A\)-module \(M\), \(B\)-module \(N\)를 고정하자. 우선 임의의 \(v\in\Hom_B(\phi_!M,N)\)에 대하여, 함수들의 합성
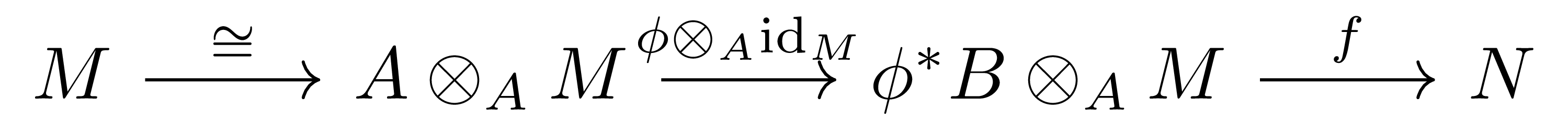
을 통해 함수 \(M \rightarrow N\)을 얻는다. 이 때 \(M \rightarrow A\otimes_AM \rightarrow \phi^\ast B\otimes_AM\)은 \(A\)-linear map들의 합성이고, \(v:\phi^\ast B\otimes M \rightarrow N\)은 \(B\)-linear map이다. 우선 임의의 \(\alpha\in A\)와 \(x\in M\)에 대하여 앞의 \(A\)-linear map들의 합성을 보면
\[\alpha\cdot_Ax\mapsto \alpha\otimes_A x\mapsto \phi(\alpha)\otimes_A x\]이고, \(B\)-linear map \(f\)에 대해서는
\[\phi(\alpha)\otimes_A x=(\phi(\alpha)1)\otimes_A x=\phi(\alpha)\cdot_B(1\otimes_A x)\]을 이용하면
\[v(\phi(\alpha)\otimes_A x)=v(\phi(\alpha)\cdot_B(1\otimes_A x))=\phi(\alpha)\cdot_B v(1\otimes_A x)\]이다. 즉, restriction of scalar를 통해 \(N\)을 \(A\)-module로 보면 위의 합성은 \(A\)-linear map인 것을 안다.
거꾸로, 임의의 \(u\in\Hom_A(M, \phi^\ast N)\)이 주어졌다 하자. 그럼 이번엔 다음 합성
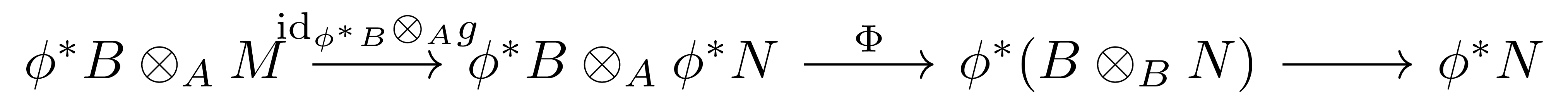
을 통해 함수 \(\phi_!M \rightarrow N\)을 얻는다. 그럼 임의의 \(\beta'\in B\)와 \(\beta\otimes_A x\in \phi^\ast B\otimes_AM\)에 대하여,
\[\Phi(\id_{\phi^\ast B}\otimes_A u(\beta'\cdot_B(\beta\otimes_Ax)))=\Phi((\beta'\beta)\otimes_Ax)=(\beta'\beta)\otimes_B x\]이고, 이는 \(B\otimes_BN\cong N\)을 통해 \((\beta'\beta)\cdot_Bx=\beta'\cdot_B(\beta\cdot_Bx)\)로 옮겨진다. 즉 위에서 정의한 함수는 \(B\)-linear map이다.
이제 위에서 정의된 두 함수가 서로의 역함수임을 확인할 수 있고, 뿐만 아니라 이들이 natural equivalence를 정의한다는 것 또한 확인할 수 있다.
또, 다음의 adjoint pair 또한 비슷한 방식으로 증명할 수 있다.
명제 6 Adjoint \(\phi^\ast\dashv\phi_\ast\)가 존재한다.
따라서 \(\phi^\ast:\lMod{B} \rightarrow\lMod{A}\)는 left adjoint이자 right adjoint이고, 따라서 모든 종류의 limit, colimit과 commute한다.
-
엄밀히 말하자면 이 식에서 첫 번째 isomorphism을 말이 되게 하기 위해서는 \(B\)가 \((A,\mathbb{Z})\)-bimodule이라는 사실을 이용해야 한다. ↩

댓글남기기