Yoneda lemma
(Locally small) category \(\mathcal{A}\)의 임의의 대상 \(A\)는 두 functor
\[\Hom_\mathcal{A}(A,-):\mathcal{A}\rightarrow\Set,\qquad \Hom_\mathcal{A}(-,A):\mathcal{A}\rightarrow\Set\]를 정의하며, 첫 번째는 covariant functor, 두 번째는 contravariant functor가 된다. (§함자, ⁋예시 4)
정의 1 Category \(\mathcal{A}\)가 주어졌다 하자.
- Covariant functor \(F:\mathcal{A}\rightarrow\Set\)이 representable functor표현 가능한 함자라는 것은 적당한 object \(A\in\obj(\mathcal{A})\)가 존재하여, \(F\)와 \(\Hom_\mathcal{A}(A,-)\)이 naturally isomorphic한 것이다.
- Contravariant functor \(F:\mathcal{A}\rightarrow\Set\)이 representable functor표현 가능한 함자라는 것은 적당한 object \(A\in\obj(\mathcal{A})\)가 존재하여, \(F\)와 \(\Hom_\mathcal{A}(-,A)\)이 naturally isomorphic한 것이다.
임의의 functor \(F\)에 대하여, 위의 조건을 만족하는 \(A\in\obj(\mathcal{A})\)와 natural isomorphism의 선택을 \(F\)의 representation표현이라 부른다.
예시 2 예를 들어, \(\id_\Set:\Set \rightarrow \Set\)은 representable이다. 이는 임의의 singleton \(\ast\)에 대하여 다음 natural isomorphism
\[\id_\Set\cong\Hom_\Set(\ast,-)\]이 성립하기 때문이다. 임의의 집합 \(A\)에 대하여, 전단사함수
\[\id_\Set(A)=A\rightarrow\Hom_\Set(\ast,A)\]는 \(A\)의 임의의 원소 \(a\)를 받아서, 그 image가 \(a\)인 함수 \(a:\ast\rightarrow A\)로 주어지며, 거꾸로 함수 \(\ast\rightarrow A\)의 image를 보면 \(A\)의 원소를 얻어낼 수 있다. 이 대응의 naturality는 임의의 함수 \(f:A \rightarrow B\)가 주어졌을 때, 임의의 \(a\in A\)에 대해 \(b=f(a)\)라 하면 \(\id_\Set(B)\rightarrow\Hom_\Set(\ast,B)\)는 그 image가 \(b\)인 함수 \(b:\ast \rightarrow B\)이고, 이것이 정확히 합성 \(\ast\overset{a}{\longrightarrow}A\overset{f}{\longrightarrow}B\)와 같기 때문에 얻어진다.
이와 관련된 가장 중요한 정리는 다음의 요네다 보조정리이다.
정리 3 (Yoneda) 임의의 functor \(F:\mathcal{A}\rightarrow\Set\)과, 임의의 \(A\in\obj(\mathcal{A})\)에 대하여, 집합 사이의 bijection
\[\Phi:\{\text{natural transformations from $\Hom_\mathcal{A}(A,-)$ to $F$}\}\rightarrow F(A);\qquad \alpha\mapsto \alpha_A(\id_A)\]가 존재한다.
증명
우선 위의 함수가 어떻게 작동하는지를 잠깐 살펴보면, \(\Hom_\mathcal{A}(A,-)\)에서 \(F\)로의 natural transformation은 임의의 대상 \(X\)에 대하여, 두 집합 \(\Hom_\mathcal{A}(A,X)\)에서 \(F(X)\)로의 함수 \(\alpha_X\)로 주어진다. 특별히 \(X=A\)인 경우, 함수 \(\alpha_A\)는 \(\Hom_\mathcal{A}(A,A)\)에서 \(F(A)\)로의 함수로 주어지며, \(\id_A\in\Hom_\mathcal{A}(A,A)\)이므로 \(\alpha_A(\id_A)\in F(A)\)이다.
이 함수가 bijection임을 보이기 위해서는 역함수를 만들면 충분하다. 즉, 임의의 원소 \(x\in F(A)\)로부터 natural transformation \(\Psi(x)\)를 만들어내야 하고, 이 때 \(\Psi(x)\)는 다시 \(\mathcal{A}\)의 임의의 대상 \(X\)에 대하여 함수 \(\Psi(x)_X:\Hom_\mathcal{A}(A,X)\rightarrow F(X)\)로 주어진다. 그런데 \(\Psi(x)\)가 natural transformation이라면, 다음의 diagram이 commute해야 한다.
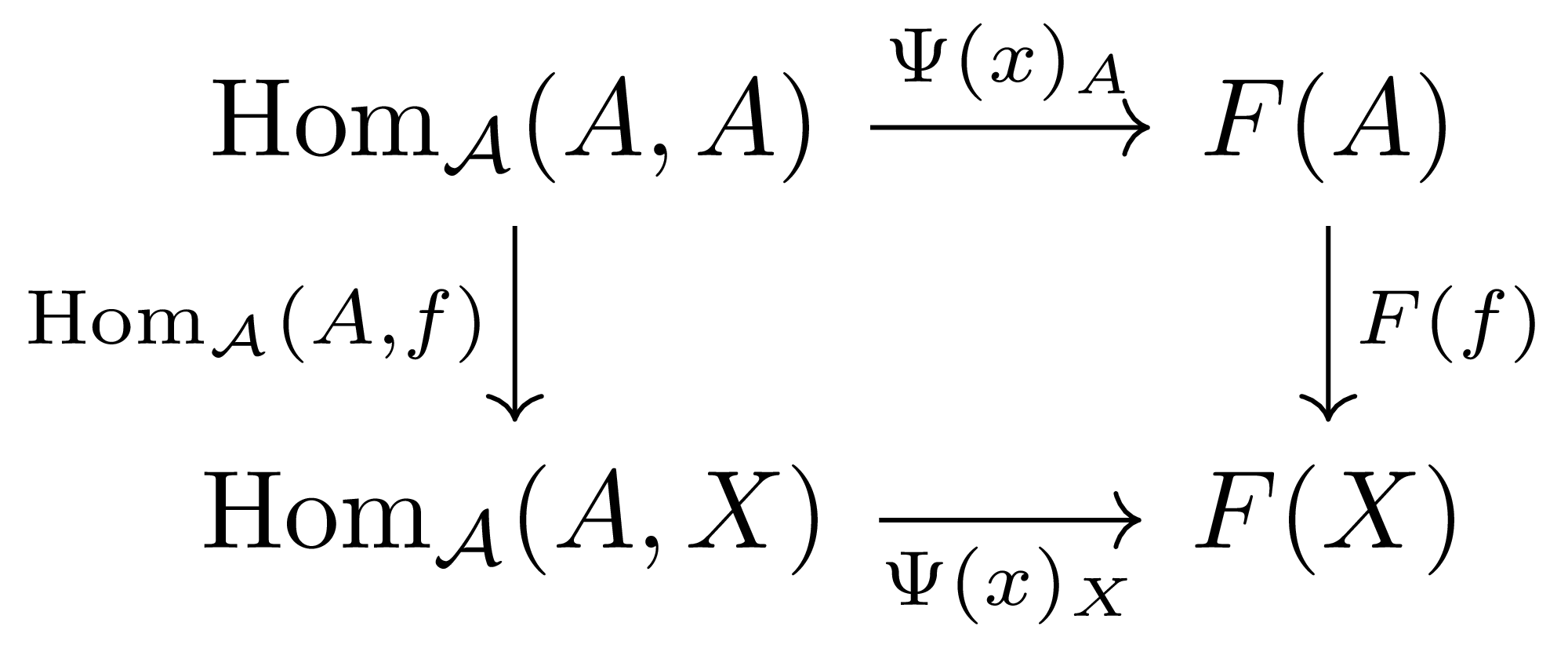
다시 \(\id_A\in\Hom_\mathcal{A}(A,A)\)를 생각하자. 그럼 오른쪽 위 방향으로 따라가면 이는 \(F(f)(\Psi(x)_A(\id_A))\)이고, 왼쪽 아래 방향을 따라가면 \(\Psi(x)_X(f)\)가 된다. 즉
\[\Psi(x)_X(f)=F(f)(\Psi(x)_A(\id_A))\]가 성립해야 한다. 한편, \(\Psi\)가 \(\Phi\)의 역함수이기 위해서는 \((\Psi\circ\Phi)(x)=x\)여야 하므로, \(\Psi\)가 어떻게 정의되었는지를 생각해보면 \(\Psi(x)_A(\id_A)\)가 정확히 \(x\)여야 한다는 것을 알 수 있다. 즉, 다음의 식
\[\Psi(x)_X(f)=F(f)(x)\]를 통하여 \(\Psi(x)\)를 정의해야만 한다. 이렇게 정의한 \(\Psi\)가 실제로 natural transformation이 된다는 것을 추가로 보여야 하지만 이는 어렵지 않다.
뿐만 아니라, 양 변을 \(\mathcal{A}\times\Set^\mathcal{A}\)에서 \(\Set\)으로의 functor로 생각하면 이 bijection은 \(\mathcal{A}\)와 \(\Set^\mathcal{A}\) 각 성분에 대해 natural하다. 이 사실은 지금 당장 사용할 것은 아니므로 언급만 하고 넘어가지만, 그 증명 또한 위의 증명과 마찬가지로 크게 어렵지는 않다. 또, duality에 의해 contravariant functor에 대한 요네다 보조정리도 존재한다.
정리 4 (Yoneda) 임의의 contravariant functor \(F:\mathcal{A}\rightarrow\Set\)과, 임의의 \(A\in\obj(\mathcal{A})\)에 대하여, 집합 사이의 bijection
\[\Phi:\{\text{natural transformations from $\Hom_\mathcal{A}(-,A)$ to $F$}\}\rightarrow F(A);\qquad \alpha\mapsto \alpha_A(\id_A)\]가 존재한다.
서술의 편의를 위해 남은 글에서는 covariant functor의 경우만 다루지만, 자명한 방식으로 contravariant functor에 대해서도 똑같은 이야기들을 할 수 있다.
Universal property
정의 1을 보면, 우리는 object \(A\)와 natural isomorphism \(F\cong\Hom_\mathcal{A}(A,-)\)의 선택을 통틀어 representation이라 부르기로 하였다. 그런데 정리 3에 의하여 natural isomorphism을 택하는 것은 \(F(A)\)의 적절한 원소를 하나 뽑아오는 것과 같다. 이를 다음과 같이 정의한다.
정의 5 Representable functor \(F:\mathcal{A}\rightarrow\Set\)가 주어졌다 하자. Natural isomorphism \(\Hom_\mathcal{A}(-,A)\cong F\)에 대하여, \(F(A)\)의 원소 \(x\in F(A)\)를 universal element라 부르고, \(A\)와 \(x\)를 묶어 universal property라 부른다.
다음 예시를 살펴보면 이를 좀 더 직관적으로 이해할 수 있다.
예시 6 두 \(k\)-벡터공간 \(V,W\)를 고정하고, category \(\Vect_k\)에서 \(\Set\)으로의 functor \(\operatorname{Bilin}(V,W;-)\)을
\[\operatorname{Bilin}(V,W;U)=\{\text{bilinear maps from $V\times W$ to $U$}\}\]으로 정의하자. 그럼 이 functor가 representable하다는 사실이 잘 알려져 있다. 즉 적당한 \(k\)-벡터공간 \(V\otimes W\)가 존재하여, 다음 natural isomorphism
\[\Hom_{\Vect_k}(V\otimes W,-)\cong\operatorname{Bilin}(V,W;-)\]이 존재한다. 이 때 natural isomorphism은 Yoneda lemma에 의하여, \(\operatorname{Bilin}(V,W;V\otimes W)\)의 하나의 원소, 즉 \(V\times W\)에서 \(V\otimes W\)로의 bilinear map으로 정의된다.
바꿔 말하자면, tensor product의 universal property는 대상 \(V\otimes W\)와, universal element \(V\times W\rightarrow V\otimes W\)가 담고 있으며, 위의 natural isomorphism이 말해주는 것이 정확히 \(V\times W\)에서 \(U\)로의 bilinear map이 주어질 때마다 (우변), 유일한 \(k\)-linear map \(V\otimes W\) (좌변)이 주어진다는 뜻이 된다.
위의 예시를 통해 다양한 분야에서 universal property를 통해 정의된 대상들이 실은 위의 꼴인 것을 확인할 수 있다. 그러나 범주론의 관점에서만 보자면 아직까지는 이들을 universal property라 부르는 이유는 정의 5에서 그렇게 이름을 붙였다는 것 외에는 찾아볼 수 없다.
이를 정당화하기 위해 category \(\mathcal{A}\)의 어떠한 대상 \(I\)가, 임의의 대상 \(A\)가 주어질 때마다 유일한 morphism \(I\rightarrow A\)를 가질 때 이를 \(\mathcal{A}\)의 initial object시작 대상라 부르자. 비슷하게 terminal object끝 대상 또한 정의한다. 그럼 명제 8은 위의 질문에 적절한 답을 준다. 즉, 이러한 대상들은 모두 적절한 카테고리의 initial (혹은 terminal) object로 생각할 수 있다. 이를 설명하기 위해서는 다음 정의가 필요하다.
정의 7 Functor \(F: \mathcal{A}\rightarrow \Set\)의 category of elements는 다음의 데이터로 이루어진 카테고리 \(\int F\)이다.
- \(\int F\)의 대상들은 \(A\in \mathcal{A}\)와 \(x\in F(A)\)로 이루어진 pair \((A,x)\)이다.
- \(\int F\)의 morphism \((A_1,x_1) \rightarrow (A_2, x_2)\)는 \(F(f)(x_1)=x_2\)를 만족하는 \(\mathcal{A}\)의 morphism \(f\)이다.
예컨대, \(\Hom_{\mathcal{A}}(A,-):\mathcal{A}\rightarrow\Set\)의 category of elements는 다음의 데이터로 구성된다.
- \(\int \Hom_\mathcal{A}(A,-)\)의 대상들은 \(X\in \mathcal{A}\)와 \(\pi\in \Hom_\mathcal{A}(A,X)\)로 이루어진 pair \((X,\pi)\)이다.
- \(\int \Hom_\mathcal{A}(A,-)\)의 morphism \(f:(X_1,\pi_1)\rightarrow(X_2,\pi_2)\)은 \(\pi_2=\Hom_\mathcal{A}(A,f)(\pi_1)=f\circ\pi_1\)을 만족하는 \(\mathcal{A}\)의 morphism이다.
즉, \(\int\Hom_\mathcal{A}(A,-)\)는 under category \({}_{A/}\mathcal{A}\)이다.
이제 다음 명제를 증명할 준비가 되었다.
명제 8 Functor \(F:\mathcal{A}\rightarrow\Set\)이 representable인 것과 \(\int F\)가 initial object를 갖는 것이 동치이다.
증명
\(F\)가 representable하다면 \(F\cong\Hom_\mathcal{A}(A,-)\)이도록 하는 적절한 \(A\)와 natural isomorphism \(\alpha\)가 존재한다. 그럼 이를 통해 \(\int F\)에서 \(\int\Hom_\mathcal{A}(A,-)\)로의 isomorphism \((X,x)\mapsto (X,\alpha_X(x))\)을 만들 수 있다. 그런데 \(\int\Hom_\mathcal{A}(A,-)={}_{A/}\mathcal{A}\)은 initial object \(\id_A\)를 갖는다.
이제 \(\int F\)가 initial object \((A,x)\)를 갖는다 하고 이로부터 natural isomorphism \(\Hom_\mathcal{A}(A,-)\Rightarrow F\)를 만들어야 한다. 우선 정리 3로부터, 우리는 bijection
\[\Phi:\{\text{natural transformations from $\Hom_\mathcal{A}(A,-)$ to $F$}\}\rightarrow F(A)\]이 존재함을 알고 있으며, 이것이 bijection임을 증명하기 위해서 우리는 \(x\in F(A)\)마다 정의되는 natural transformation \(\Psi(x):\Hom_\mathcal{A}(A,-)\Rightarrow F\)를 다음 식
\[\Psi(x)_X(f)=F(f)(x)\]으로 정의했었다. 한편 \(\int F\)에서, \((A,x)\)가 initial이라는 뜻은 임의의 \((X,y)\in\int F\)를 가져올 때마다 \(\mathcal{A}\)에서의 morphism \(f:A \rightarrow X\)가 유일하게 존재하여 \(F(f)(x)=y\in F(X)\)인 것이다. 그런데 위의 식에 따라 \(F(f)(x)=\Psi(x)_X(f)\)이고, \(X\)를 고정하면 \(y\)는 \(F(X)\)에서 임의로 택해올 수 있으므로 이를 다시 말하면 임의의 \(y\in F(X)\)가 주어질 때마다, \(y=\Psi(x)_X(f)\)를 만족하는 \(f\in\Hom_\mathcal{A}(A,X)\)를 반드시 유일하게 찾아올 수 있다는 뜻이다. 즉, \(\Psi(x)_X\)가 isomorphism이고 \(X\) 역시 임의로 택할 수 있으므로 \(\Psi(x)\)가 \(\Hom_\mathcal{A}(A,-)\)에서 \(F\)로의 natural isomorphism을 정의한다.
이제 임의의 category의 initial object는 항상 유일한 isomorphism에 대해 유일하게 결정되므로, universal property 또한 유일한 isomorphism에 대해 유일하게 결정된다.
참고문헌
[Rie] Emily Riehl. Category Theory in Context. Dover Publications, 2016.

댓글남기기