K

Grad. student in mathematics

극한 범주의 정의

우선 다음 정의부터 시작한다. 임의의 두 category \(\mathcal{A},\mathcal{B}\)에 대하여, functor \(\mathcal{A}\rightarrow \mathcal{B}\)가 constant functor라는 것은 \(\mathcal{A}\)의 모든 대상이 \(\mathcal{B}\)의 고정된 대상 \(B\)로 옮겨지고, 모든 morphism은 \(\id_B\)로 옮겨지는 것을 의미한다. 약간의 abuse of notation을 통해 위의 constant functor를 \(B:\mathcal{A}\rightarrow \mathcal{B}\)로 적기도 한다.

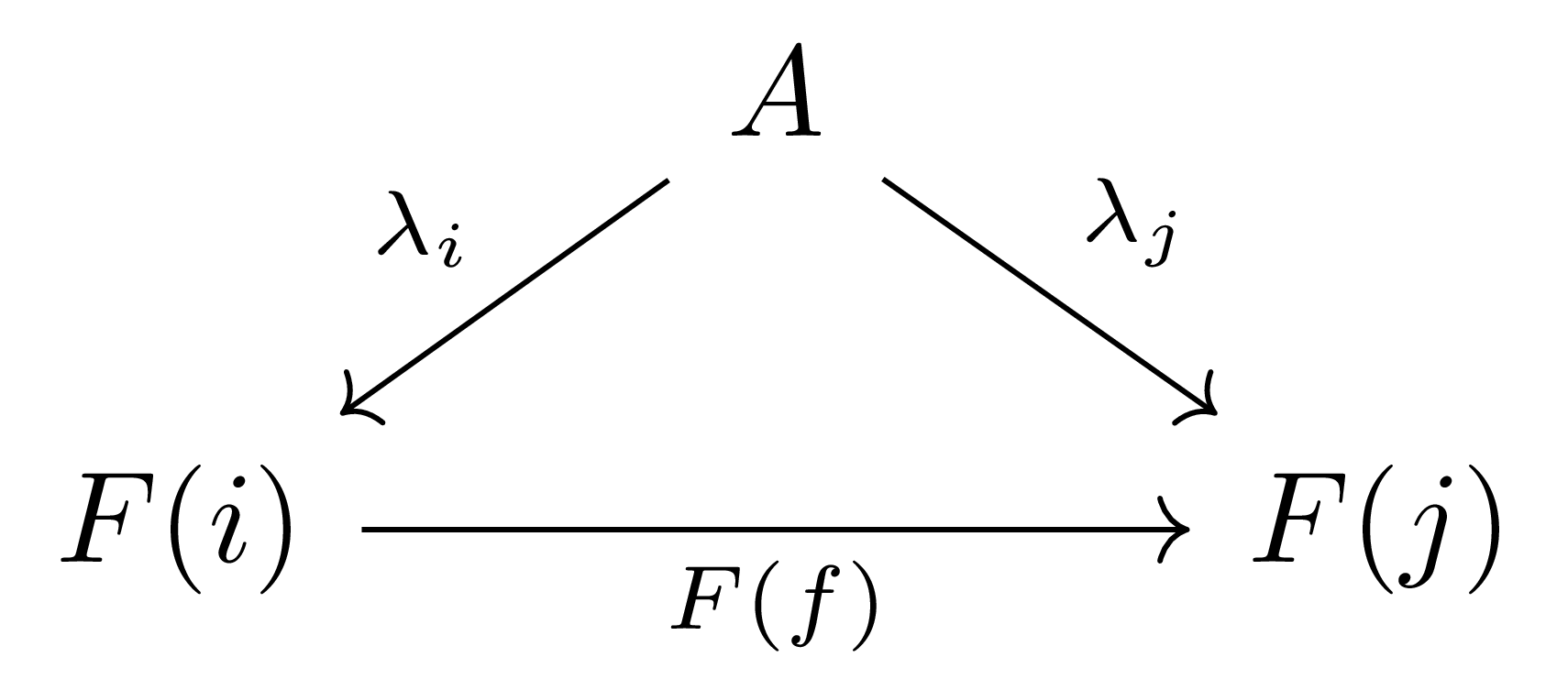
정의 1 Category \(\mathcal{A}\)에서 정의된 diagram1 \(F:\mathcal{I}\rightarrow \mathcal{A}\)를 생각하자. 대상 \(A\in \mathcal{A}\)와, constant functor \(A: \mathcal{I}\rightarrow \mathcal{A}\)에 대하여, natural transformation \(\lambda:A \Rightarrow F\)를 \(F\) 위에서의 cone\(F\) 위에서의 뿔이라 부르고, \(A\)를 이 cone의 꼭짓점apex, 그리고 각각의 \(\lambda_i:A \rightarrow F(i)\)들을 leg다리라 부른다. \(\mathcal{A}^\op\)에서의 cone을 cocone이라 부른다.

임의의 diagram \(F:\mathcal{I}\rightarrow \mathcal{A}\)을 고정하자. 꼭짓점 \(A\)를 가지는 \(F\) 위에서의 cone과 morphism \(A' \rightarrow A\)가 주어졌다 하면, 이를 통해 자연스럽게 꼭짓점 \(A'\)를 가지는 \(F\) 위에서의 cone을 정의할 수 있다. 따라서

\[\Cone(A, F)=\{\text{cones over $F$ with apex $A$}\}\]

으로 정의하면, \(\Cone(-,F)\)는 \(\mathcal{A}\)에서 \(\Set\)으로의 contravariant functor가 된다. \(\mathcal{I}\)가 poset \((\mathbb{Z},\leq)\)로 만들어진 category일 때 정의 1을 그려보면 다음과 같다.

Cone

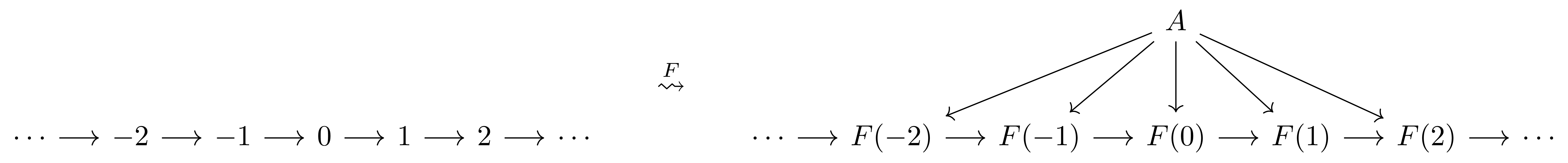
각 삼각형들이 모두 commute한다는 것이 \(\lambda\)가 natural transformation이라는 것에 의해 얻어진다. 이제 morphism \(A' \rightarrow A\)가 주어졌다면, \(\Cone(A',F)\)는 아래 그림과 같이 정의된다.

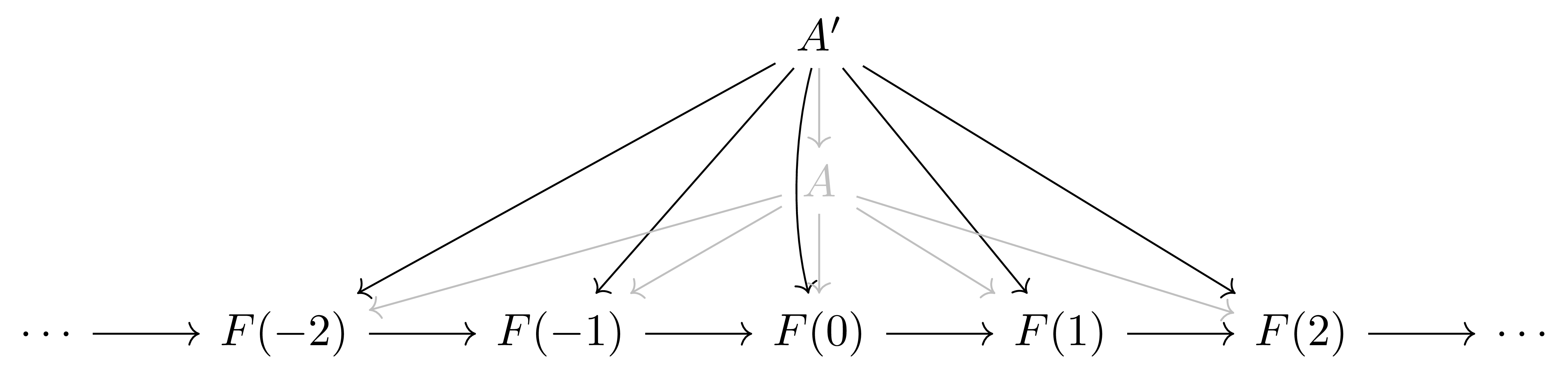
Functoriality_of_cone

따라서, contravariant functor \(\Cone(-,F): \mathcal{A}\rightarrow \Set\)이 representable할 경우, 이 functor의 representation을 \(F\)의 limit으로 정의한다.

정의 2 Functor \(\Cone(-,F)\)의 representation \(\lambda:\lim F \Rightarrow F\)를 \(F\)의 limit극한이라 부른다.

비슷하게 \(F\) 위에서의 cocone이 주어지면 이를 통해 covariant functor \(\Cone(F,-):\mathcal{A}\rightarrow \Set\)을 정의할 수 있고, 이 functor의 representation을 colimit이라 부른다.

극한의 보편성질

한편, 우리는 §표현가능한 함자, ⁋명제 7에서 representation을 universal property를 이용해 표현하는 방법을 살펴보았다. 우리 상황에 이를 적용하기 위해 functor \(\Cone(-,F):\mathcal{A}\rightarrow \Set\)의 category of elements를 생각하면,

  • \(\int\Cone(-,F)\)의 대상들은 pair \((B, \mu)\)이다. 여기서 \(B\)는 \(\mathcal{A}\)의 대상이고, \(\mu\in\Cone(B,F)\)이다.
  • \(\int\Cone(-,F)\)의 morphism \((B,\mu)\rightarrow (B',\mu')\)은 조건 \(\Cone(f,F)(\mu)=\mu'\)를 만족하는 \(f:B' \rightarrow B\)이다.

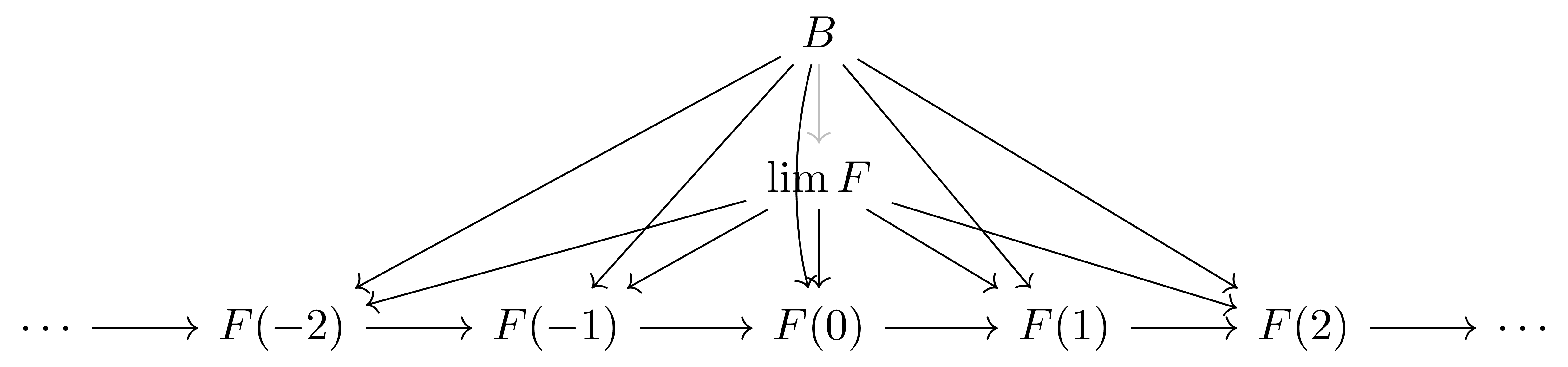
즉 \(\int\Cone(-,F)\)는 (임의의 꼭짓점을 가질 수 있는) cone들의 category로 생각할 수 있다. 이제 §표현가능한 함자, ⁋명제 7의 dual 버전을 생각하면 \(F\)의 limit \(\lambda:\lim F\Rightarrow F\)는 \(\int\Cone(-,F)\)의 terminal object이다. 가령 앞선 예시의 경우로 이를 조금 더 풀어 써 보면, 다음의 commutative diagram

universal_property-1

이 주어질 때마다 유일한 \(f:B \rightarrow\lim F\)가 존재하여 다음 diagram을 commute하게 해야한다.

universal_property-2

물론 일반적으로 어떤 diagram의 limit (혹은 colimit)이 존재한다는 보장은 없다.

정의 3 Diagram \(F:\mathcal{I}\rightarrow \mathcal{A}\)이 small이라는 것은 indexing category \(\mathcal{I}\)가 small인 것이다. 임의의 small diagram이 항상 limit을 갖는 category \(\mathcal{A}\)를 complete category완비범주라 부른다. 임의의 small diagram이 항상 colimit을 갖는 category \(\mathcal{A}\)를 cocomplete categoory여완비범주이라 부른다. Small limit들을 보존하는 functor를 continuous functor라 부르고, small colimit들을 보존하는 functor를 cocontinuous functor라 부른다.

예시 4 \(\Set\)은 complete category이다. 이 사실을 증명할 때 중요하게 사용되는 것은 §표현가능한 함자, ⁋예시 2의 natural isomorphism

\[A\cong\Hom_\Set(\ast, A)\qquad\text{for all $A\in\Set$}\tag{1}\]

이다. 임의의 (small) diagram \(F: \mathcal{I}\rightarrow \Set\)이 주어졌다 하자. 만일 \(F\)의 limit이 존재한다면

\[\Cone(A,F)\cong \Hom_\Set(A,\lim F)\qquad\text{for all $A\in\Set$}\]

이고 특별히 \(\Cone(\ast,F)\cong\Hom_\Set(\ast,\lim F)\cong \lim F\)이므로, 남은 것은 natural transformation \(\lambda:\lim F\Rightarrow F\)를 찾고, 이 cone이 universal하다는 것을 보이는 것이다. Natural transformation \(\lambda:\lim F\Rightarrow F\)는 commuting 조건들을 만족하는 함수들 \(\lambda_i:\lim F\rightarrow F(i)\)들에 의해 결정되므로, 이를 위해서는 우선 \(\Cone(\ast,F)\)의 원소에 대해 생각할 필요가 있다.

\(\Cone(\ast,F)\)의 원소 \(\mu:\ast\Rightarrow F\)는 마찬가지로 commuting 조건들을 만족하는 leg들 \(\mu_i:\ast\rightarrow F(i)\)들의 모임이다. 그런데 이들 \(\mu_i\)들은 다시 식 (1)에 의해 \(F(i)\)의 원소로 취급할 수 있으므로, 각각의 \(i\in\mathcal{I}\)마다

\[\Cone(\ast,F)\overset{\lambda_i}{\longrightarrow}F(i);\quad (\mu:\ast\Rightarrow F)\mapsto \mu_i\in F(i)\qquad\text{for all $i\in \mathcal{I}$}\]

으로 정의해주면 이들을 모아둔 natural transformation \(\lambda:\lim F\Rightarrow F\)가 원하는 조건을 만족한다.

극한 범주의 예시

Category \(\mathcal{I}\)의 모양에 따라, limit을 다양한 이름으로 부르기도 한다.

예시 5 (Inverse limit) 특별히 \(\mathcal{I}=\omega^\op\)인 경우를 생각하자. 여기서 \(\omega\)는 ordinal \(\omega\)에 정의된 poset구조를 이용해서 정의된 category이며, 따라서 이 category로 index가 주어진 diagram은 다음 꼴

inverse_limit

이다. 이 diagram의 limit을 inverse limit이라 부르는데, 직관적으로 \(\lim F\)를 그려보면 다음 그림

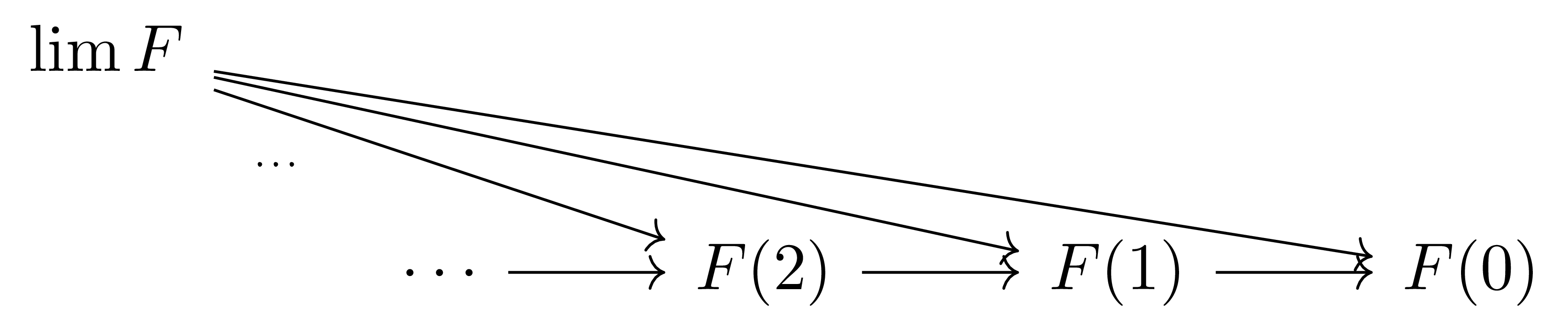
inverse_limit-2

와 같이 \(\lim F\)가 모든 \(F(i)\)들보다 작은 것처럼 보이므로 이를 limit이라 부를 만하다.

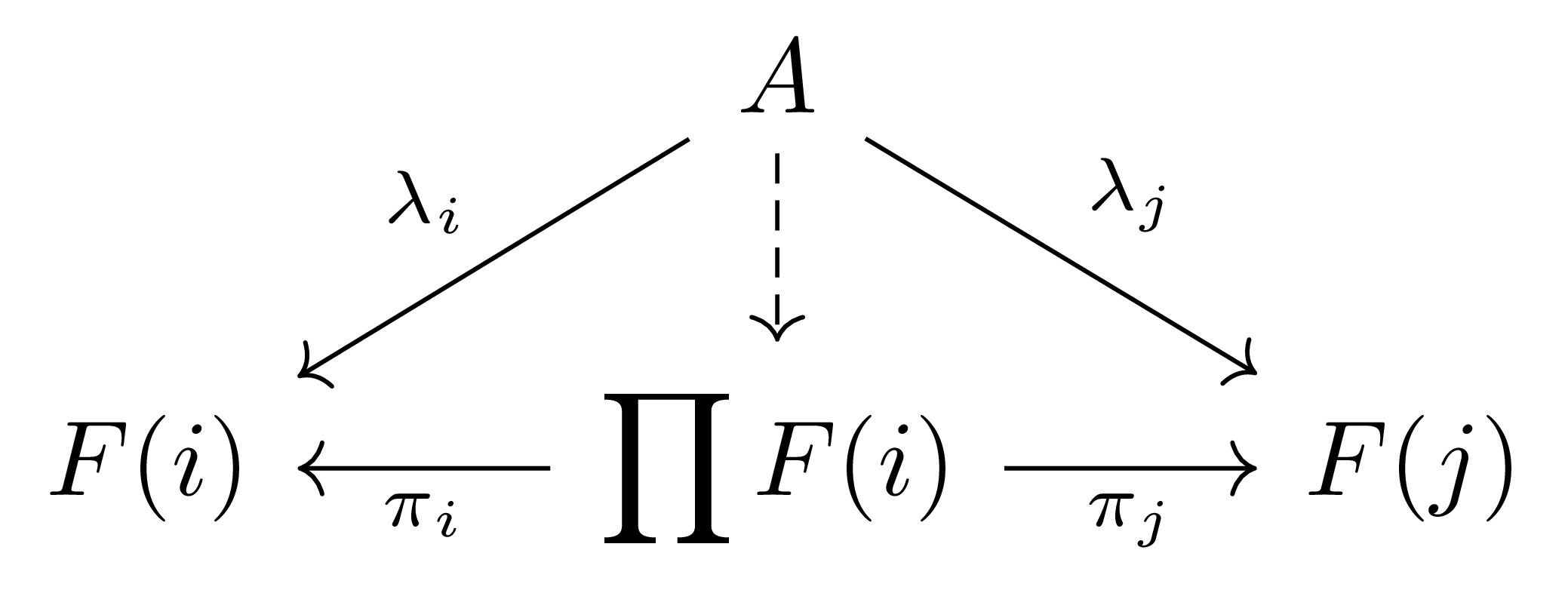
예시 6 (Product) Discrete category는 morphism이 identity morphism밖에 없는 category를 일컫는다. 그럼 이 diagram의 cone들 \(\lambda:A\Rightarrow F\)에서 \(\lambda\)의 naturality는 어떠한 조건도 부여하지 않으며, 따라서 그냥 morphism들의 family \((\lambda_i:A \rightarrow F(i))_{i\in \mathcal{I}}\)들이 된다. 이렇게 discrete category로 index가 주어진 diagram의 limit \(\pi:\lim F\Rightarrow F\)을 product곱라 부르고, \(\pi_i\)들을 projection이라 부르며, 이 경우에 \(\lim F\) 대신 \(\prod F(i)\)와 같은 표기를 사용한다.

특별히 예시 6의 경우에서 limit cone \(\pi:\prod F(i)\Rightarrow F\)의 universal property를 다시 써 보면 다음과 같다.

\(\mathcal{A}\)의 임의의 대상 \(A\)와 morphism들 \(\lambda_i:A \rightarrow F(i)\)가 주어질 때마다, 유일한 \(A \rightarrow \prod F(i)\)가 존재하여 다음 diagram

universal_property_of_product

이 commute한다.

이해를 돕기 위해 이 예시를 예시 4에서 정의한 집합들의 limit인 경우로 제한하면 이 universa; property는 정확히 [집합론] §집합의 곱, ⁋정리 3에서 정의한 집합의 곱의 universal property와 같다.

예시 7 (Equalizer) 다음 category

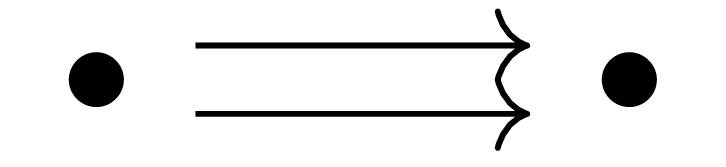
equlizer_indexing_category

를 생각하자. 그럼 이 category로 index가 주어진 diagram은

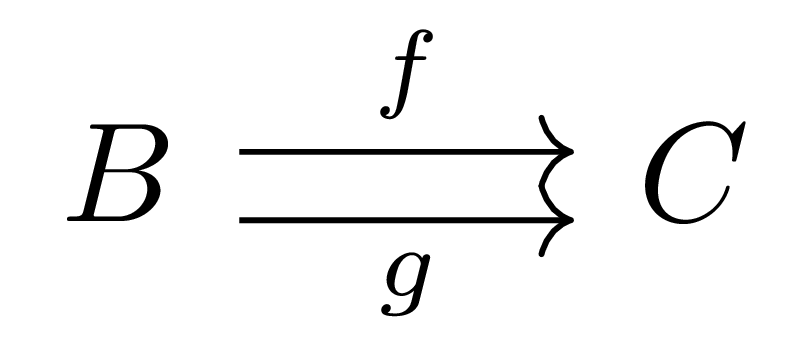
equalizer_diagram

와 같은 꼴이며, 다음 diagram

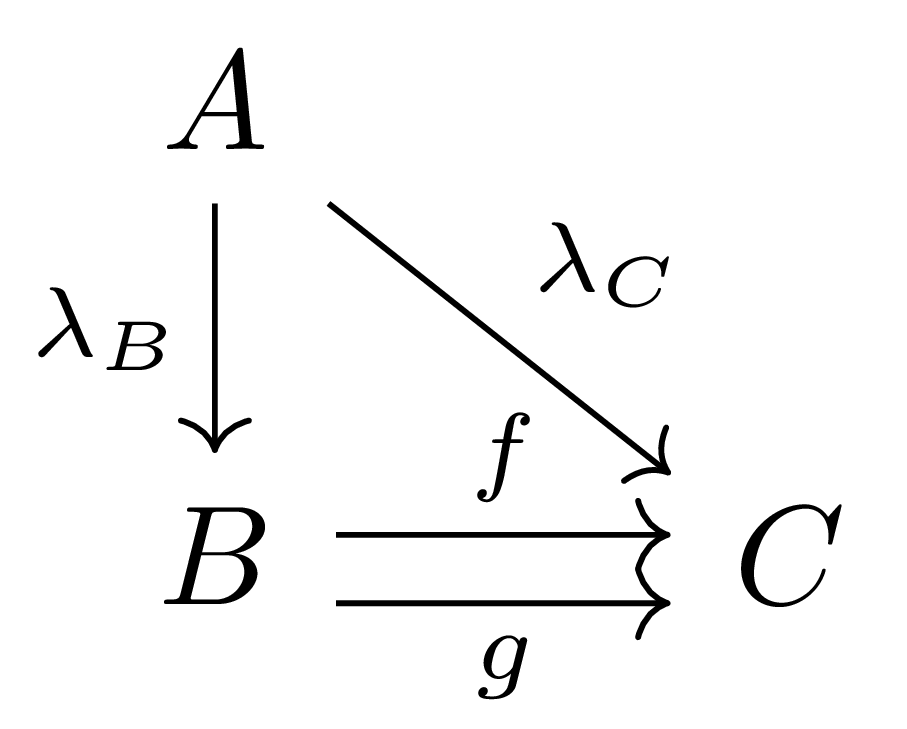
equalizer_cone

이 cone이라는 것은 두 조건 \(\lambda_C=f\circ\lambda_B\), \(\lambda_C=g\circ\lambda_B\)이 만족되는 것이고, 따라서 \(\lambda_B\circ f=\lambda_B\circ g=\lambda_C\)인 것이다. \(A\)가 cone이라면 \(\lambda_C\)는 \(\lambda_B\)로부터 이와 같은 식으로 정의되므로, 유효한 정보는 \(\lambda_B\circ f=\lambda_B\circ g\)를 만족하는 \(\lambda_B:A \rightarrow B\) 뿐임을 알 수 있다. 그럼 이 diagram의 limit은 이러한 cone들 가운데 universal한 것을 뜻한다.

예시 6과 예시 7을 적절히 조합하면 \(\Set\)에서의 diagram \(\mathcal{I}\rightarrow \Set\)의 limit을 적당한 equalizer diagram으로 쓸 수 있다. 예시 4에서 살펴본 것과 같이 limit cone의 원소 \(\lambda\in\lim F=\Cone(\ast,F)\)는 모든 \(\mathcal{I}\)의 morphism \(f\)마다 다음 diagram

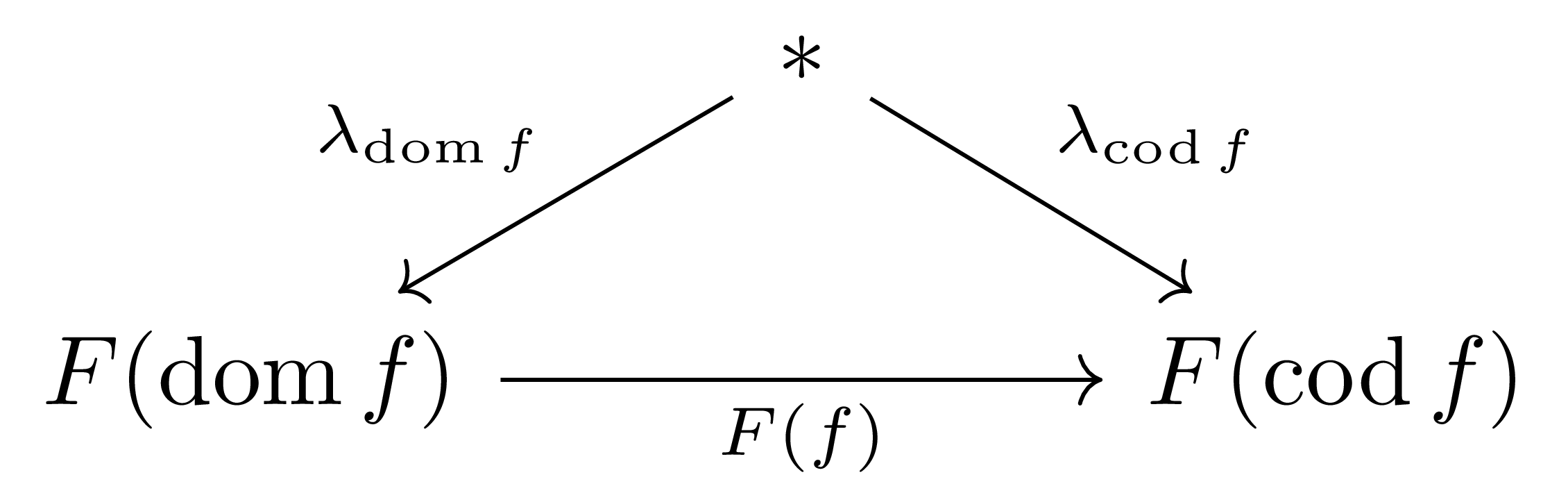
equalizer_seq

을 commute하게 하도록 하는 \((\lambda_i)_{i\in\mathcal{I}}\)이다. 즉, 거꾸로 말하자면 \(\lim F\)는 \(\prod F(i)\)의 원소들 중 위의 조건을 만족하는 것들을 모아둔 것이므로, \(\prod_{i\in\mathcal{I}}F(i)\)에서 \(\prod_{f\in\Hom(\mathcal{I})}F(\operatorname{cod}f)\)로의 두 함수 \(a,b\)를 \(\lambda=(\lambda_i)_{i\in\mathcal{I}}\in\prod_{i\in\mathcal{I}}F(i)\)를 받아서,

  • \(a(\lambda)\)는 \(f\in\Hom(\mathcal{I})\)번째 성분에 \(\lambda_{\operatorname{cod}f}\in F(\operatorname{cod}f)\)가 있는 \(\prod_{f\in\Hom(\mathcal{I})}F(\operatorname{cod}f)\)의 원소 \((\lambda_{\operatorname{cod}f})_f\),
  • \(b(\lambda)\)는 \(f\in\Hom(\mathcal{I})\)번째 성분에 \(F(f)(\lambda_{\operatorname{dom}f})\in F(\operatorname{cod}f)\)가 있는 \(\prod_{f\in\Hom(\mathcal{I})}F(\operatorname{cod}f)\)의 원소 \((F(f)(\lambda_{\operatorname{dom}f}))_f\)

을 주는 함수로 정의하자. 그럼 위의 diagram의 commutativity는 정확히 이 둘이 같을 것을 요구하며, 따라서 \(\lim F\)는 다음의 equalizer limit diagram

equalizer_limit_diagram

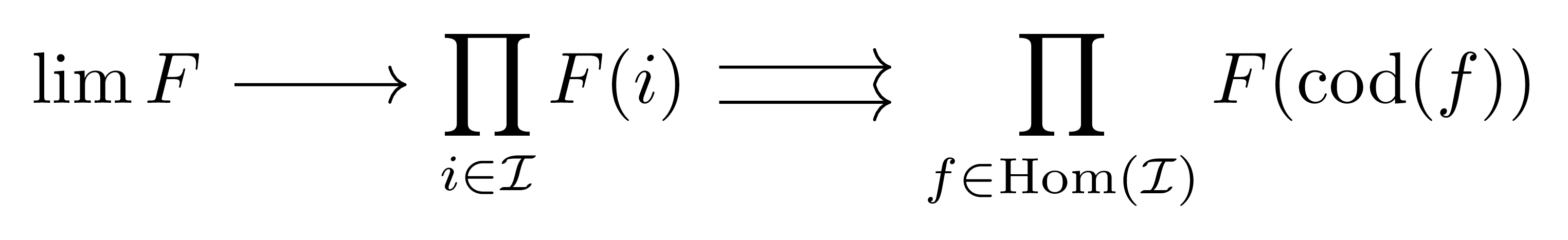
을 통해 얻어질 수 있다. 우리는 이 증명에서 \(\Set\) category의 성질을 쓰긴 했지만, 적절한 방식으로 이를 범주론의 언어로 바꾸어 쓸 수 있고 따라서 임의의 category가 product와 equalizer를 갖는다면 limit 또한 갖는다는 것을 보일 수 있다.

예시 8 (Fiber product) 마지막으로 다음 category

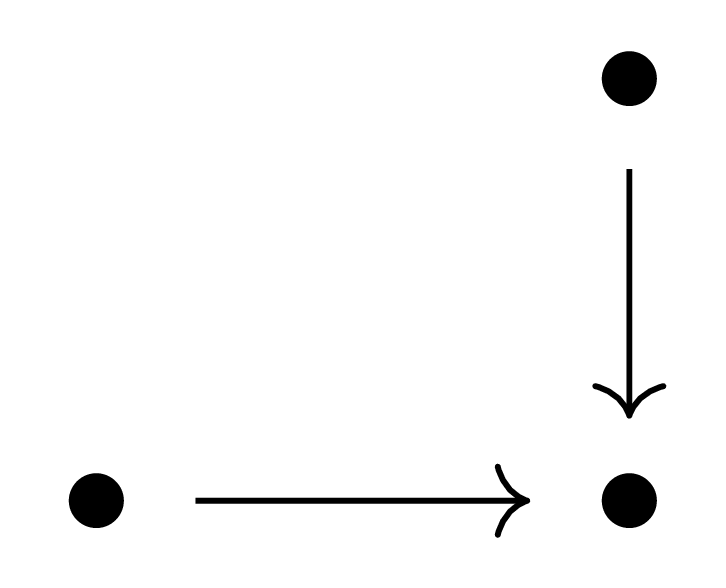
fiber_indexing_category

를 생각하자. 그럼 이 category로 index가 주어진 diagram은 다음 꼴

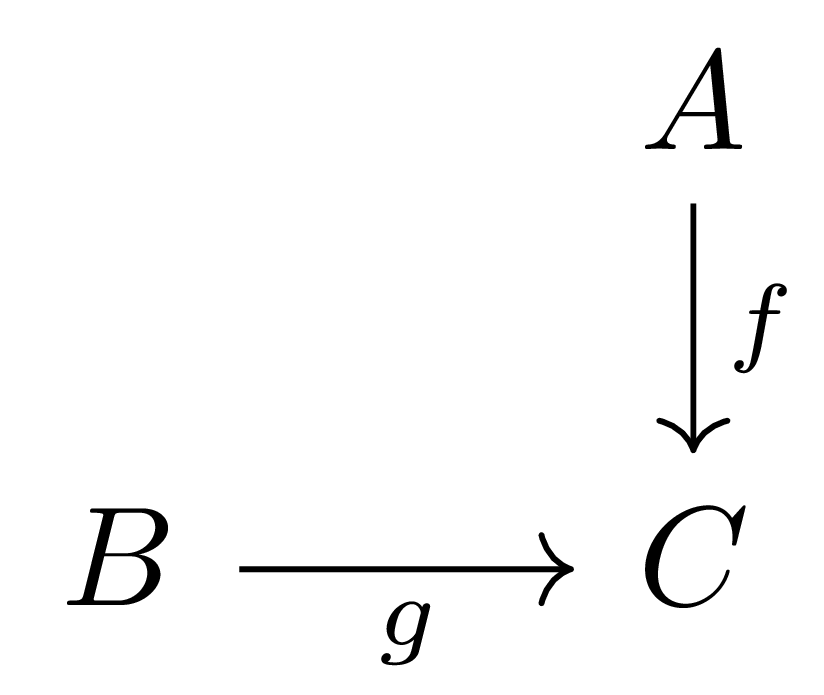
fiber_diagram

이며, 이 diagram의 limit은 조건 \(g\circ b=f\circ a\)을 만족하는 \(A\overset{a}{\longleftarrow} X\overset{b}{\longrightarrow}B\) 중 universal한 것으로 주어진다. 이를 fiber product라 부르고 \(A\times_C B\)와 같이 표기한다. 이를 나타내는 다음과 같은 diagram

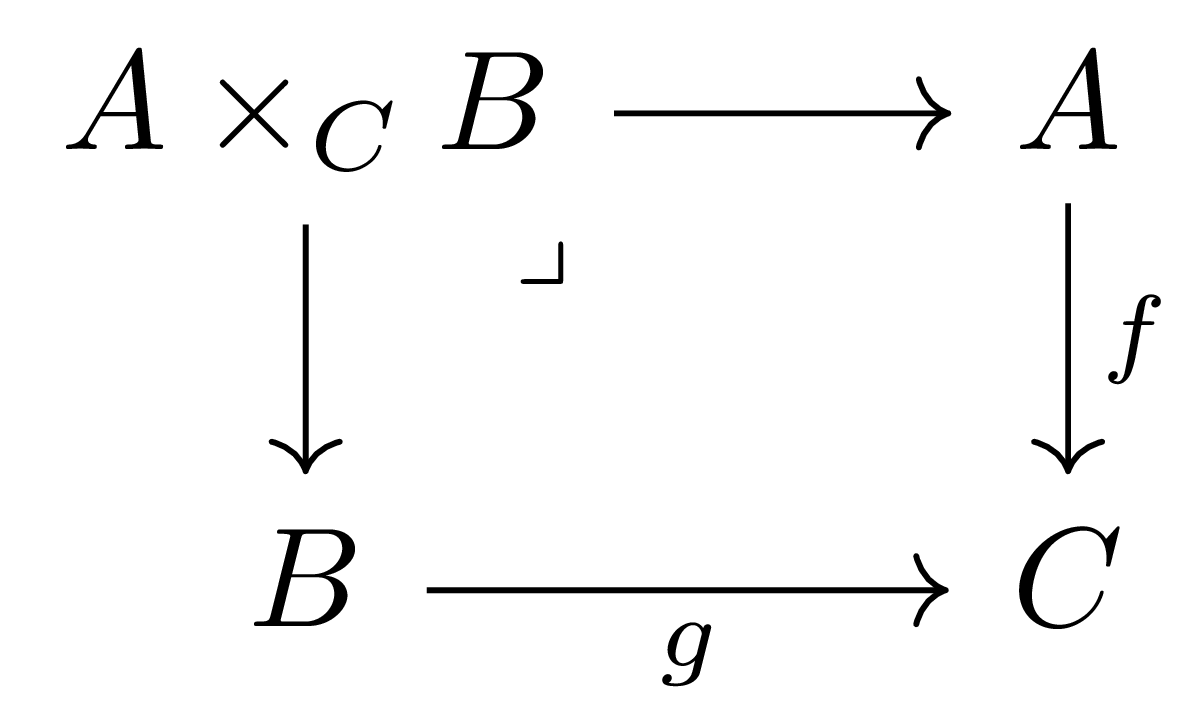
fiber_diagram_limit

을 fiber diagram이라 부르고, 이것이 fiber diagram임을 표기하기 위해 fiber product 쪽에 꺽쇠 \(\lrcorner\)를 그려 표기한다.

위의 예시들을 colimit으로 바꿔주면 direct limit, coproduct, coequalizer 그리고 fiber coproduct의 개념을 얻는다. 특히 colimit을 coproduct가 포함된 적절한 coequalizer diagram으로 나타낼 수 있고, \(\Set\)은 coproduct \(\coprod\)과 coequalizer를 모두 가지므로 cocomplete하다는 사실 또한 알 수 있다.

극한과 \(\Hom\)

한편 임의의 small diagram \(F: \mathcal{I}\rightarrow \mathcal{A}\)와 임의의 \(A\in \mathcal{A}\)에 대하여, 합성

\[\Hom_\mathcal{A}(A,-)\circ F:\mathcal{I}\rightarrow \mathcal{A}\rightarrow \Set\]

을 \(\Hom_\mathcal{A}(A,F-)\)으로 적자. 그럼 이는 \(\mathcal{I}\)에서 \(\Set\)으로의 diagram이다. 예시 4에 의하여 \(\Set\)은 complete category이므로, 이 diagram의 limit \(\lim \Hom_\mathcal{A}(A,F-)=\Cone(\ast,\Hom_\mathcal{A}(A,F-))\)이 존재한다.

이는 \(\prod_{i\in \mathcal{I}}\Hom_\mathcal{A}(A, F(i))\)의 원소들 중, 모든 \(f:i \rightarrow j\)에 대해 다음의 compatibility condition

compatibility

을 만족하는 것들이므로, 정확히 \(\Cone(A,F)\)이고 따라서

\[\lim \Hom_\mathcal{A}(A, F-)\cong\Cone(A,F)\]

가 성립한다. 한편, \(F\)가 limit을 갖는다면

\[\Cone(A,F)\cong\Hom_\mathcal{A}(A,\lim F)\]

이 성립하므로 다음 정리를 얻는다.

정리 9 임의의 diagram \(F:\mathcal{I}\rightarrow \mathcal{A}\)가 limit을 갖는다면 다음 natural isomorphism

\[\lim\Hom_\mathcal{A}(A, F-)\cong\lim\Hom_\mathcal{A}(A, F-)\]

이 존재한다.

즉, \(\Hom_\mathcal{A}(A,-):\mathcal{A}\rightarrow\Set\)은 continuous functor이다. 동일한 주장이 \(\Hom_\mathcal{A}(-, A)\)와 colimit에 대해서도 성립한다.

결합법칙

마지막으로 다음 명제를 소개한다.

명제 10 임의의 bifunctor \(F: \mathcal{I}\times \mathcal{J}\rightarrow \mathcal{A}\)에 대하여, 만일 두 극한

\[\lim_{i\in \mathcal{I}}\lim_{j\in \mathcal{J}}F(i,j),\qquad \lim_{j\in \mathcal{J}}\lim_{i\in \mathcal{I}} F(i,j)\]

가 모두 \(\mathcal{A}\)에서 존재한다면, 이들은 isomorphic하다.

비슷한 정리가 colimit에 대해서도 성립한다. 즉 limit과 colimit은 각각 결합법칙을 만족한다. 그러나 일반적으로 limit과 colimit의 순서를 바꿀 수는 없으며, 일반적으로 할 수 있는 최선은 universal property를 사용하여 (isomorphism이 아닐 수 있는) 다음의 canonical morphism

\[\colim_{i\in \mathcal{I}}\lim_{j\in \mathcal{J}} F(i,j) \rightarrow \lim_{j\in \mathcal{J}}\colim_{i\in \mathcal{I}} F(i,j)\]

을 얻는 것이 전부이다.

참고문헌

[Rie] Emily Riehl. Category Theory in Context. Dover Publications, 2016.

  1. 여기서 diagram이란 그냥 functor \(F: \mathcal{I} \rightarrow \mathcal{A}\)를 의미한다. 이 용어는 특별히 \(\mathcal{I}\)가 partially ordered set을 category로 보있을 때, functor \(F\)는 \(I\)를 index set으로 갖는 \(\mathcal{A}\)의 object들의 directed system을 만드는 것으로 생각할 수 있으므로 특히 직관적이다. ↩

댓글남기기