Gluing lemma
앞서 살펴본 §부분공간, ⁋명제 8는 연속함수 $f:X \rightarrow Y$가 주어졌다 할 때, 이를 §부분공간, ⁋명제 6의 두 조건 중 하나를 만족하는 부분집합들의 family로 제한한 것이 연속임을 말해준다. 특히 이 조건은 다음 두 조건
- $(A_i)$가 $X$의 open covering이거나,
- $(A_i)$가 $X$의 locally finite closed covering인 경우
두 경우가 해당한다. 거꾸로 이러한 조건을 만족하는 $(A_i)$와 그 위에서 정의된 연속함수들 $f_i$들이 주어졌을 때, 이들이 $X=\bigcup A_i$ 위에서의 연속함수를 지정하는지의 여부를 생각할 수 있다.
보조정리 1 집합 $X$와 §부분공간, ⁋명제 6의 두 조건 중 하나를 만족하는 부분집합들의 family $(A_i)$가 주어졌다 하자. 만일 연속함수들의 family $(f_i: A_i \rightarrow Y)$가 다음 조건
\[f_i\vert_{A_i\cap A_j}=f_j\vert_{A_i\cap A_j}\qquad\text{for all $i,j$}\]을 만족한다면, 이들을 확장하여 생기는 함수 $f:X \rightarrow Y$는 연속함수이다.
증명
우선 함수 $f$는 [집합론] §집합의 합, ⁋명제 2에 의해 얻어진다. 이 함수가 연속이라는 것은 §부분공간, ⁋명제 8에서 얻어진다.
연속함수들의 준층
수학, 특히 기하학의 많은 부분에서 살펴보는 구조들은 위상공간 위에 추가적인 데이터가 주어진 구조이다. 이들을 위해서는 위와 같은 과정을 다루는 도구가 필요하다.
Category $\Open(X)$를 ordered set $(\mathcal{T}, \subseteq)$를 category로 본 것으로 정의하자. 즉, 이들의 대상들은 열린집합들이며, $U\subseteq V$일 때마다 화살표 $U\hookrightarrow V$가 유일하게 존재한다.
정의 2 위상공간 $X$에 대하여, contravariant functor $\mathscr{F}:\Open(X)^\op \rightarrow \Set$을 $X$ 위에 정의된 집합들의 presheaf준층라 부른다.
이제 $\mathscr{F}$는 contravariant이므로, 열린집합 사이의 inclusion $U\hookrightarrow V$가 주어질 때마다 morphism $\rho_{VU}: \mathscr{F}(V)\rightarrow \mathscr{F}(U)$가 주어지며, $\mathscr{F}$는 합성을 보존하므로 $U\hookrightarrow V\hookrightarrow W$가 주어졌다면 $\rho_{WU}=\rho_{VU}\circ\rho_{WV}$가 성립해야 한다.
예시 3 두 위상공간 $X, Y$가 주어졌다 하고, $\mathscr{F}$를 다음과 같이 정의하자.
- 임의의 열린집합 $U$에 대하여, $\mathscr{F}(U)=\Hom_\Top(U, Y)$이다.
- 열린집합 $U\subseteq V$가 주어졌을 때, $\rho_{VU}:\mathscr{F}(V) \rightarrow \mathscr{F}(U)$는 $V$에서 정의된 연속함수를 $U$로 제한하는 restriction map이다.
그럼 $\mathscr{F}$는 presheaf가 된다.
위의 예시를 일반화하여 다음과 같은 정의를 내린다.
정의 4 위상공간 $X$ 위에서 정의된 presheaf $\mathscr{F}$가 주어졌다 하자.
- 임의의 열린집합 $U\subseteq X$에 대하여, $\mathscr{F}(U)$의 원소들을 $U$에서의 section이라 부른다. 특별히 $\mathscr{F}(X)$의 원소들은 global section이라 부른다.
- 열린집합 $U\subseteq V$에 대하여, $\rho_{VU}:\mathscr{F}(V) \rightarrow \mathscr{F}(U)$를 $V$에서 $U$로의 restriction map이라 부른다.
- 특별히 열린집합들 $U\subseteq V$와 $s\in \mathscr{F}(V)$에 대하여, $\rho_{UV}(f)\in \mathscr{F}(U)$를 간단히 $s\vert_U$로 표기한다.
한편 위의 정의 2에서, $\Set$은 적절한 카테고리, 예를 들어 $\Ab$와 같은 카테고리로 바꿀 수도 있다. 가령 예시 3에서 $Y=\mathbb{R}$이었다면, $\mathbb{R}$ 위에 정의된 덧셈을 사용하여 연속함수들의 덧셈을 정의할 수도 있었을 것이며, 그럼 $\mathscr{F}(U)$는 abelian group의 구조를 가지게 되었을 것이다. 이러한 경우 $\mathscr{F}$를 $X$ 위에 정의된 abelian group들의 presheaf라 부른다. 편의상 앞으로 presheaf $\mathscr{F}: \Open(X)^\op \rightarrow \mathcal{A}$를 $\mathcal{A}$-valued presheaf라 부르기로 한다. Presheaf 중 위의 gluing condition (보조정리 1)을 만족하는 것들을 sheaf라 부르는데, 이는 다음 글에서 정의한다.
준층의 예시들
다음으로 presheaf의 몇 가지 예시들을 살펴본다.
예시 5 (Skyscraper sheaf) 고정된 위상공간 $X$와 한 점 $i_x:\{x\}\hookrightarrow X$가 주어졌다 하고, 대상 $A\in \mathcal{A}$를 고정하자. 그럼 다음의 식
\[(i_x)_\ast A(U)=\begin{cases}A&\text{if $x\in U$,}\\T&\text{if $x\not\in U$,}\end{cases}\qquad \text{$T$ a terminal object in $\mathcal{A}$}\]으로 주고, restriction map은 $\id_A$ 혹은, terminal object $T$를 이용해 주면 이는 presheaf를 정의한다. 이를 skyscraper sheaf라 부른다.
예시 6 (Constant presheaf) 이번에는 고정된 위상공간 $X$와 대상 $A\in \mathcal{A}$를 고정하고, 모든 열린집합마다 $A$를 대응시키고 restriction map들은 모두 $\id_A$로 주자. 그럼 이는 presheaf를 정의하며, 이를 constant presheaf라 부른다.
다음 예시들은 임의의 presheaf로부터 새로운 presheaf를 얻어내는 방법들을 보여준다.
예시 7 $X$ 위에 정의된 presheaf $\mathscr{F}$가 주어졌을 때, 임의의 열린집합 $U$에 대하여 $\mathscr{F}\vert_U$를 다음 식
\[\mathscr{F}\vert_U(V)=\mathscr{F}(V)\quad\text{for all open $V\subseteq U$}\]으로 정의할 수 있다. 그럼 $\mathscr{F}\vert_U$는 presheaf가 된다. (§부분공간, ⁋보조정리 2)
예시 8 (Pushforward) 연속함수 $f:X \rightarrow Y$를 고정하고, $X$ 위에 정의된 presheaf $\mathscr{F}$가 주어졌다 하자. 그럼 $\mathscr{F}$의 $f$에 의한 pushforward밂 $f_\ast \mathscr{F}$를 다음 식
\[f_\ast \mathscr{F}(U)=\mathscr{F}(f^{-1}(U))\]을 통해 정의한다.
줄기
한편, $X$ 위에 정의된 함수를 결정짓는 것은 당연히 $x\in X$에서의 함숫값이다. 이것이 집합으로서 $X$ 위에 정의된 함수와 다른 점은 $X$ 위에 정의된 위상구조로 인하여, 이 점 $x$ 근방에서 어떠한 일이 일어나는지를 같이 살펴볼 수 있다는 것이다. 이러한 직관을 바탕으로 다음을 정의한다.
정의 9 위상공간 $X$ 위에서 정의된 presheaf $\mathscr{F}$를 생각하자. 임의의 점 $x\in X$에 대하여, 점 $x$에서의 stalk줄기 $\mathscr{F}_x$를
\[\mathscr{F}_x=\varinjlim_{x\in U}\mathscr{F}(U)\]으로 정의한다. $\mathscr{F}_x$의 원소들을 점 $x$에서의 germ싹이라 부른다.
특히 $\mathscr{F}$가 complete category valued presheaf라면 $\mathscr{F}_x$가 항상 잘 정의된다. 한편 concrete category에서 limit의 표현을 직접적으로 나타내보면
\[\mathscr{F}_x=\{(s,U)\mid x\in U\in\mathscr{T},s\in\mathscr{F}(U)\}/\mathnormal{\sim}\]이고, 여기서 동치관계 $\sim$은
\[(s,U)\sim(t,V)\iff\text{$\exists$ open neighborhood $W\subseteq U\cap V$ of $x$ satisfying $\rho_{UW}(s)=\rho_{VW}(t)$}\]을 통해 정의된다. 즉 직관적으로 $\mathscr{F}_x$의 원소 $(s,U)$들은 $x$에서의 함숫값 $s(x)$와, $x$ 근방에서 $s$의 국소적인 정보1를 추가로 갖고 있는 대상이라 생각할 수 있다.
편의상 임의의 $s\in \mathscr{F}(U)$에 대하여, $s$의 $\mathscr{F}(U) \rightarrow \mathscr{F}_x$에 의한 image를 $s_x$로 적는다.
준층들 사이의 사상
정의 10 고정된 위상공간 $X$ 위에서 정의된 두 presheaf $\mathscr{F}, \mathscr{G}:\Open(X) \rightarrow \mathcal{A}$ 사이의 natural transformation을 presheaf morphism준층 사상으로 정의한다.
즉 $X$ 위에서 정의된 $\mathcal{A}$-valued presheaf들의 카테고리는 functor category $[\Open(X)^\op, \mathcal{A}]$이다. 이를 $\PSh(X, \mathcal{A})$로 표기하며, 문맥상 혼동의 여지가 없을 때에는 $\PSh(X)$로만 적기도 한다. 여담으로 예시 8의 $f_\ast$는 functor $\PSh(X, \mathcal{A})\rightarrow \PSh(Y, \mathcal{A})$이다.
우리에게 직관을 주는 예시 2를 생각해보면, 열린집합 $U$에 대하여 정의된 $\phi(U):\mathscr{F}(U) \rightarrow \mathscr{G}(U)$는 $\phi:\mathscr{F}\rightarrow \mathscr{G}$를 열린집합 $U$로 제한하여 얻어지는 함수라 생각할 수 있으므로, 이를 종종 $\phi(U)$ 대신 $\phi\vert_U$로 적는다.
한편 limit cone의 universal property에 의해 다음 명제가 성립한다.
명제 11 위상공간 $X$ 위에 정의된 presheaf들 사이의 morphism $\phi:\mathscr{F}\rightarrow\mathscr{G}$가 주어졌다 하자. 그럼 임의의 $x\in X$에 대하여, stalk들 사이의 morphism $\phi_x:\mathscr{F}_x\rightarrow\mathscr{G}_x$가 자연스럽게 유도된다.
다음 예시들은 위의 준층의 예시들 아래에 있었어야 했지만, 아직 presheaf morphism을 정의하지 않았었기 때문에 뒤로 밀렸다.
예시 12 (Sheaf Hom) 두 presheaf $\mathscr{F}, \mathscr{G}$를 고정하고, 임의의 $U$에 대하여
\[\mathscr{Hom}(\mathscr{F},\mathscr{G})(U)=\Hom_{\PSh(U)}(\mathscr{F}\vert_U, \mathscr{G}\vert_U)\]으로 정의한다.
예시 13 (Product) 위상공간 $X$ 위에 정의된 presheaf들의 family $(\mathscr{F}_i:\Open(X) \rightarrow \Set)_{i\in I}$에 대하여, 이들의 product $\prod_{i\in I} \mathscr{F}_i$를
\[\left(\prod_{i\in I} \mathscr{F}_i\right)(U)=\prod_{i\in I} \mathscr{F}_i(U)\]으로 정의할 수 있다.
위와 같은 정의를 이용하여 category $\mathcal{A}$에 정의된 구조, 예를 들면 product나 coproduct, limit, colimit, monoidal product 등을 $\PSh(X, \mathcal{A})$에 옮겨올 수 있다. 특히 $\PSh(X, \Ab)$는 $\Ab$ 위에 정의된 monoidal structure $(\Ab,\otimes, \mathbb{Z})$를 물려받으며 여기에서의 monoidal object는 $\PSh(X, \Ring)$이다. 같은 맥락에서 다음 예시를 이해할 수 있다.
예시 14 위상공간 $X$ 위에 정의된 $\Ring$-valued presheaf $\mathscr{O}_X$에 대하여, left $\mathscr{O}_X$-module object $\mathscr{F}\in\PSh(X,\Ab)$을 간단히 $\mathscr{O}_X$-module이라 부른다.
가환준층
지금까지 우리는 presheaf가 어떤 카테고리에서 값을 갖는지를 무시해왔는데, 이제 우리는 특별히 카테고리 $\Ab$에서 값을 갖는 presheaf들을 살펴본다.
정의 15 위상공간 $X$에 대하여, contravariant functor $\Open(X)\rightarrow\Ab$을 abelian presheaf라 부른다.
정의 16 위상공간 $X$ 위에 정의된 abelian presheaf들 사이의 morphism $\phi:\mathscr{F}\rightarrow\mathscr{G}$가 주어졌다 하자. 그럼 $\phi$의 presheaf kernel핵 준층 $\ker\phi$는
- 각각의 열린집합 $U\subseteq X$마다, $U\mapsto \ker(\phi(U))$
-
포함관계에 있는 두 열린집합 $U\subseteq V$마다 다음의 diagram
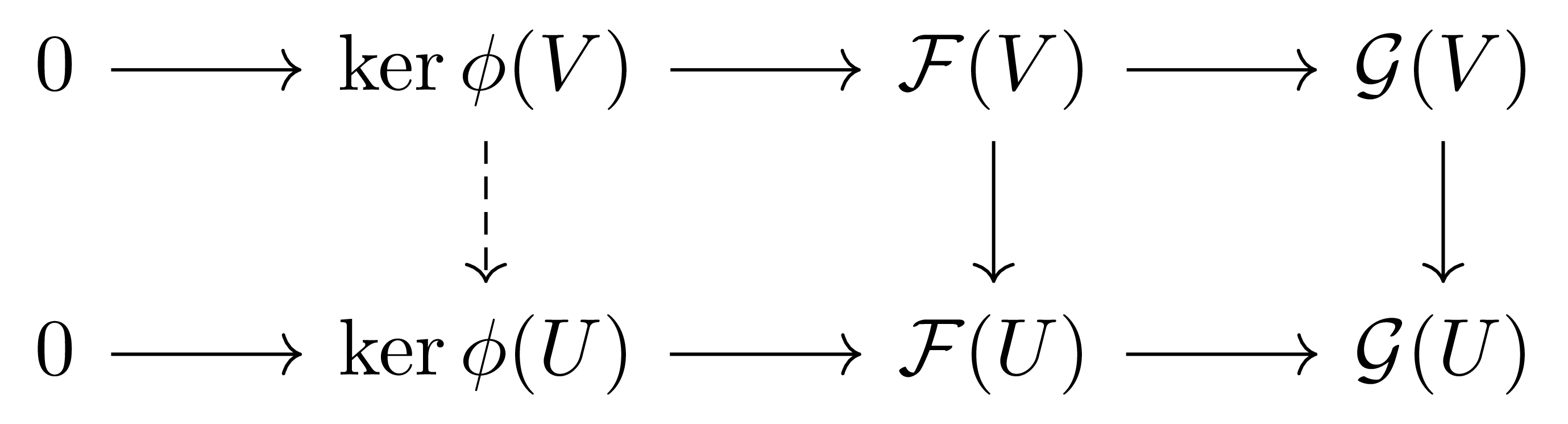
을 통해 유일하게 결정되는 restriction map $\rho_{VU}:\ker(\phi(V))\rightarrow\ker(\phi(U))$
으로 이루어진 데이터이다.
이 정의에서, $\rho_{VU}$는 $\ker(\phi(U))$의 universal property로부터 유일하게 결정되는 restriction map이다.
보조정리 17 위에서 정의한 $\ker\phi$는 $X$ 위에서의 (abelian) presheaf이다.
증명
다음의 diagram
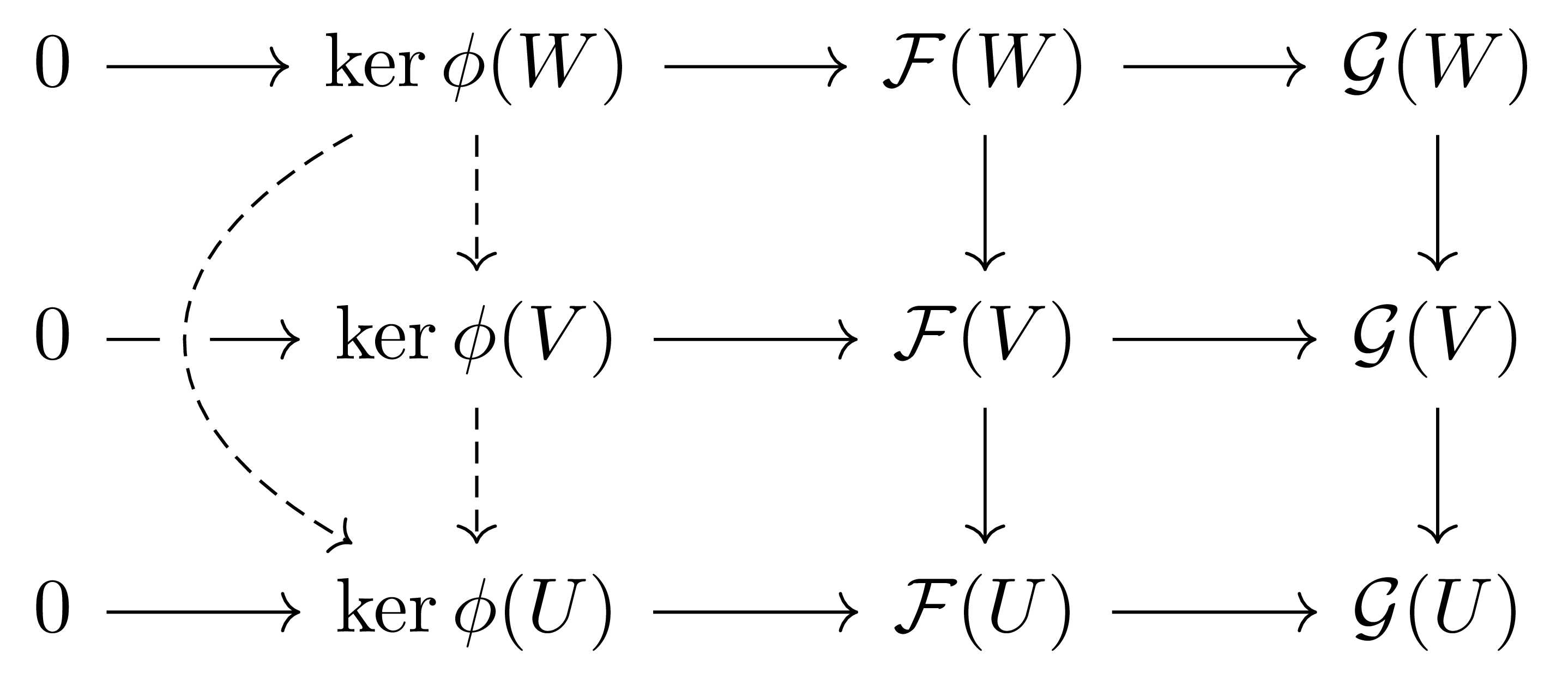
와 kernel의 universal property에 의해 자명하다.
이와 마찬가지 방법으로, presheaf cokernel, presheaf image, presheaf coimage 혹은 presheaf quotient 등등을 모두 정의할 수 있다. 따라서 주어진 위상공간 $X$ 위에서 정의된 abelian presheaf들의 카테고리 $\PSh(X,\Ab)$은 abelian category가 된다.
참고문헌
[Vak] R. Vakil, The rising sea: Foundation of algebraic geometry. Available online.
-
가령, $X=\mathbb{R}$이라 하면 $\mathbb{R}$의 한 점 $x$에서의 미분을 정의하기 위해서는 $x$의 아주 작은 근방에서의 $f$의 값들만 알면 충분하다. 이러한 점에서 $f’(x)$는 $x$가 갖고 있는 국소적인 정보 중 하나라 할 수 있다. ↩
댓글남기기