완전열

[다중선형대수학] 카테고리에서 우리는 module의 성질에 대해 살펴본다. [대수적 구조]에서 우리는 module의 성질을 살펴보긴 하였으나, 해당 카테고리에서는 일반적인 대수적인 구조들에서 공통적으로 정의하고 증명할 수 있는 것들에 초점을 두었다면, 이 카테고리에서는 조금 더 module만이 갖는 성질에 집중한다는 차이가 있다.

예컨대 특별히 field \(\mathbb{K}\) 위에 정의된 module들, 즉 \(\mathbb{K}\)-벡터공간들에 대한 결과들은 [선형대수학]에서 살펴보았었는데, 여기에서 \(\mathbb{K}\)-벡터공간들의 기저를 잡거나 이를 사용하여 linear map을 행렬로 표현하는 등의 일들은 일반적인 대수적 구조에서 기대하기는 힘든 일들이다.

이와 같은 관점에서[다중선형대수학] 카테고리의 가장 큰 목표는 [선형대수학]에서의 결과들을 \(\mathbb{K}\) 대신 일반적인 ring \(A\)로 바꾸어 최대한 일반화하는 것이라 할 수 있다. 한편 해당 카테고리의 글들은 비전공자 혹은 저년차 학부생을 염두에 두고 작성한 글들로 특히 [범주론]의 언어를 거의 사용하지 않았었는데, 이와 같이 [선형대수학]의 내용들을 현대적인 언어로 바꾸는 것 또한 목표 중 하나이다.

이 카테고리의 글들에서 \(A\)-module은 항상 left \(A\)-module을 뜻하며, 적절한 방식으로 동일한 논증을 right \(A\)-module에 대해서도 펼칠 수 있다. 같은 글 안에 left \(A\)-module과 right \(A\)-module이 동시에 등장해야 할 경우에는 혼동을 피하기 위해 이렇게 생략하지 않지만, 이러한 경우에도 left \(A\)-module을 right \(A\)-module로, right \(A\)-module을 left \(A\)-module로 서로 바꾸면 동일한 논증을 펼칠 수 있다.

가군의 합

이번 글의 목표는 몇 가지 exact sequence들을 소개하고, splitting exact sequence의 개념을 정의하는 것이다. 우선 다음의 간단한 보조정리부터 시작한다.

보조정리 1 \(A\)-module \(M\)의 submodule들의 family \((N_i)_{i\in I}\)에 대하여, 교집합 \(\bigcap_{i\in I} N_i\)는 \(M\)의 submodule이다.

증명

[선형대수학] §벡터공간의 기저, ⁋보조정리 3의 증명은 \(\mathbb{K}\)가 field라는 사실을 사용하지 않았으므로 해당 증명을 동일하게 사용하면 된다.

정의 2 \(A\)-module \(M\)의 부분집합 \(X\)가 주어졌다 하자. 그럼 \(X\)를 포함하는 \(M\)의 submodule 중 가장 작은 것을 \(\langle X\rangle\)로 적고, 이를 \(X\)에 의해 생성되는 submodule이라 부른다. 이 경우 \(X\)를 \(\langle X\rangle\)의 생성집합_{generating set}이라 부른다.

만일 \(M\)의 어떤 submodule \(N\)에 대하여, \(N=\langle X\rangle\)이도록 하는 유한집합 \(X\)를 찾을 수 있다면 \(N\)이 finitely generated_유한생성이라 부른다.

그럼 다음이 성립한다.

명제 3 \(A\)-module \(M\)의 임의의 부분집합 \(X\)에 대하여, \(\langle X\rangle\)은 \(X\)의 원소들로 이루어진 임의의 일차결합들의 집합과 같다.

증명

[선형대수학] §벡터공간의 기저, ⁋보조정리 4과 동일하게 증명하면 된다.

특별히 \(A\)-module \(M\)의 submodule들의 family \((N_i)_{i\in I}\)가 주어졌다 하자. 그럼 \(M\)의 부분집합 \(\bigcup N_i\)로 생성된 \(M\)의 submodule \(\left\langle \bigcup N_i\right\rangle\)을 \(\sum N_i\)로 표기한다. 이제 각각의 \(i\)에 대하여, \(N_i\)는 \(M\)의 submodule이므로 inclusion들 \(N_i \hookrightarrow M\)이 존재한다. 이로부터 다음의 canonical morphism

\[\bigoplus_{i\in I} N_i \rightarrow M\]

이 존재한다. 한편 \(\bigoplus N_i\)는 canonical inclusion들 \(N_i\hookrightarrow\bigoplus_{i\in I}N_i\)의 합집합에 의해 생성되고, 위의 canonical morphism에 의한 이 합집합의 image가 \(\bigoplus N_i\)이므로 다음이 성립한다.

명제 4 위에서 정의한 canonical morphism \(\bigoplus N_i \rightarrow M\)의 image가 \(\sum N_i\)이다.

즉 다음의 exact sequence

\[\bigoplus_{i\in I} N_i \rightarrow M \rightarrow M\bigg/\sum_{i\in I} N_i \rightarrow 0\tag{$\ast$}\]

가 존재한다.

이번에는 \(A\)-module \(M\)의 submodule들의 family \((N_i)_{i\in I}\)가 주어졌다 하고, canonical surjection들 \(M \twoheadrightarrow M/N_i\)가 주어졌다 하자. 그럼 이들로부터 다음의 canonical morphism

\[M \rightarrow \prod_{i\in I} M/N_i\]

이 주어진다. 다음 명제 또한 자명하다.

명제 5 위에서 정의한 canonical morphism \(M \rightarrow \prod_{i\in I} M/N_i\)의 kernel이 \(\bigcap N_i\)이다.

즉, 다음의 exact sequence

\[0 \rightarrow \bigcap_{i\in I} N_i \rightarrow M \rightarrow\prod_{i\in I} M/N_i\]

이 존재한다.

가군의 직합과 합

주어진 \(A\)-module \(M\)과 \(M\)의 submodule들의 family \((N_i)_{i\in I}\)에 대하여, 만일 canonical morphism \(\bigoplus N_i \rightarrow M\)이 isomorphism이라면, \(M\)을 \(N_i\)들의 direct sum이라 부른다. 이를 위해서는 우선 \((\ast)\)로부터 \(M=\sum N_i\)여야 함을 안다. 즉 \(M\)의 모든 원소들이 \(N_i\)의 원소들의 일차결합으로 표현되어야 한다. 한편, canonical morphism \(\bigoplus N_i \rightarrow M\)이 injective라는 것은 이렇게 일차결합을 적는 방법이 유일하다는 것과 동치임을 확인할 수 있다. 더 일반적으로 다음이 성립한다.

명제 6 위와 같은 상황에서 다음이 모두 동치이다.

1. \(\sum_{i\in I} N_i=\bigoplus_{i\in I} N_i\)이다.
2. 만일 \(x_i\in N_i\)를 만족하는 \(x_i\)들에 대하여 \(\sum_{i\in I} x_i=0\)이라면 모든 \(i\)에 대하여 \(x_i=0\)이다.
3. 임의의 \(j\in I\)에 대하여, \(N_j\)와 \(\sum_{i\neq j} N_i\)의 교집합이 \(0\)이다.

증명

처음 두 조건의 동치관계는 자명하며, 또 \(\bigoplus N_i\)를 좌표별로 써 보면 첫 번째 조건이 마지막 조건을 함의하는 것도 자명하다. 이제 마지막 조건을 가정하고 두 번째 조건을 보이자. \(\sum x_i=0\)을 만족하는 \(x_i\in N_i\)들이 주어졌다 하자. 그럼 임의의 \(j\in I\)에 대하여,

\[x_j=\sum_{i\neq j}(-x_i)\]

이고, 마지막 조건을 가정한다면 위의 식으로부터 \(x_j=0\)이어야 하므로 증명이 완료된다.

보조부분가군

다음 명제는 특별히 \(M\)이 두 개의 submodule \(N_1,N_2\)의 direct sum일 때 명제 6을 조금 더 직관적으로 살펴보도록 도와준다.

명제 7 \(A\)-module \(M\)의 두 submodule \(N_1,N_2\)가 주어졌다 하자. 그럼 다음의 두 exact sequence

\[0 \longrightarrow N_1\cap N_2 \overset{\Delta}{\longrightarrow} N_1\oplus N_2 \overset{i_1-i_2}{\longrightarrow} N_1+N_2\longrightarrow 0\]

와

\[0 \longrightarrow M/(N_1\cap N_2)\overset{\Delta'}{\longrightarrow}(M/N_1)\oplus(M/N_2)\overset{p_1-p_2}{\longrightarrow}M/(N_1+N_2)\longrightarrow 0\]

이 존재한다. 여기서 \(i_k,p_k\)는 각각 canonical morphism들

\[i_k: N_k \rightarrow N_1+N_2,\qquad p_k:M/N_k \rightarrow M/(N_1+N_2)\]

이며 \(\Delta, \Delta'\)는 각각 다음의 식

\[\Delta(x)=(x,x),\qquad \Delta'(x+(N_1+N_2))=(x+N_1,x+N_2)\]

으로 정의된 morphism들이다.

이에 대한 증명은 단순 계산이므로 생략한다. 어쨌든 첫 번째 exact sequence를 설명하자면,

\[N_1\oplus N_2=\{(x_1,x_2)\mid x_k\in N_k\}\]

이므로 \(M\) 안에서 \(N_1\)과 \(N_2\)이 어떻게 놓여있든지 \(N_1\)과 \(N_2\)의 원소는 \(N_1\oplus N_2\) 안에서는 각각 \((x_1,0)\) 그리고 \((0,x_2)\)꼴의 원소로 나타나기 때문에 이들은 서로 다른 것으로 취급된다. 특히 \(x\in N_1\cap N_2\)이더라도, \(x\)가 \(0\)이 아닌 이상 \(x\in N_1\)과 \(x\in N_2\)는 \(N_1\oplus N_2\) 안에서는 다른 원소이다. 그런데

\[i_1-i_2:N_1\oplus N_2 \rightarrow N_1+N_2;\qquad (x_1,x_2)\mapsto x_1-x_2\]

를 통해 이를 \(N_1+N_2\)로 보내고 나면 이러한 방식으로 다르게 취급된 원소들은 그 image가 \(0\)이 되어야 하고, 따라서 \(i_1-i_2\)의 kernel이 정확히 \(N_1\cap N_2\)가 된다.

한편, 우리는 다음과 같이 정의한다.

정의 8 임의의 \(A\)-module \(M\)과 \(M\)의 두 submodule \(N_1, N_2\)에 대하여, 만일 \(M\)이 \(N_1\)과 \(N_2\)의 direct sum이라면 \(N_1,N_2\)를 서로에 대한 supplementary submodule_{보조부분가군}이라 부른다. 만일 \(M\)의 submodule \(N\)이 supplementary submodule을 갖는다면 \(N\)을 \(M\)의 direct summand라 부른다.

즉, 이와 같은 상황에서 \(N_1+N_2=M\)이고 \(N_1\cap N_2=0\)이다. 그럼 이를 이용하여 canonical morphism \(M \rightarrow M/N_1\)의 정의역을 \(N_2\)로 제한한 것이 isomorphism이고, 비슷하게 \(M \rightarrow M/N_2\)의 정의역을 \(N_1\)으로 제한한 것이 isomorphism임을 확인할 수 있다.

분해완전열

마지막으로 splitting exact sequence를 정의하기 전에 다음 보조정리를 소개한다. 이에 대한 증명은 [호몰로지 대수학] §Diagram chasing, ⁋명제 1에 있다.

보조정리 9 (Four lemma) 각 행들이 exact인 commutative diagram

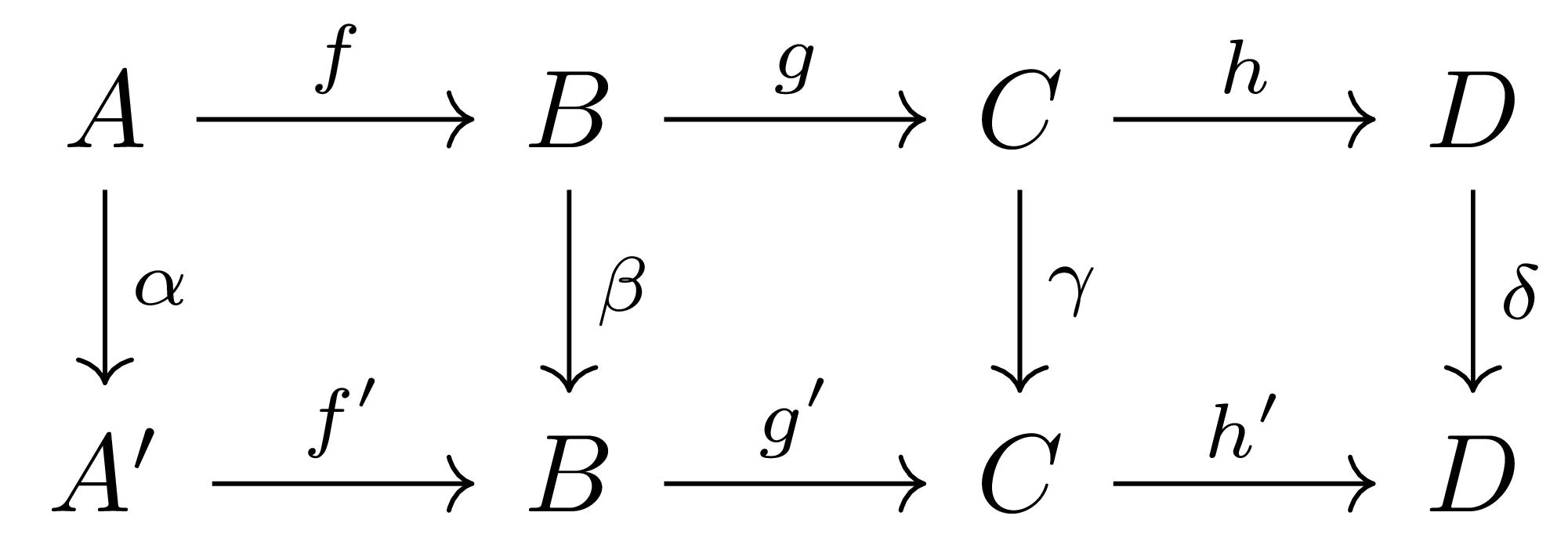
이 주어졌다 하고, \(\alpha\)가 전사이고, \(\delta\)가 단사라 가정하자. 그럼

1. 만일 \(\gamma\)가 전사라면 \(\beta\) 또한 전사이다.
2. 만일 \(\beta\)가 단사라면 \(\gamma\) 또한 단사이다.

이제 다음 명제를 통해 splitting exact sequence를 정의한다. Splitting exact sequence는 다음의 exact sequence

\[0\rightarrow N_1\hookrightarrow N_1\oplus N_2\twoheadrightarrow N_2 \rightarrow 0\]

와 같은 형태의 exact sequence를 의미하는데, 이를 정확히 풀어쓰자면 다음과 같다.

명제 10 \(A\)-module들의 exact sequence

\[0\longrightarrow M \overset{u}{\longrightarrow}L \overset{v}{\longrightarrow}N \longrightarrow 0\]

에 대하여, 다음 조건들이 모두 동치이다.

1. \(u\)의 linear retraction \(r:L \rightarrow M\)이 존재한다. ([집합론] §Retraction과 section, ⁋정의 2)
2. \(v\)의 linear section \(s:N \rightarrow L\)이 존재한다. ([집합론] §Retraction과 section, ⁋정의 2)

3. 다음의 diagram

   

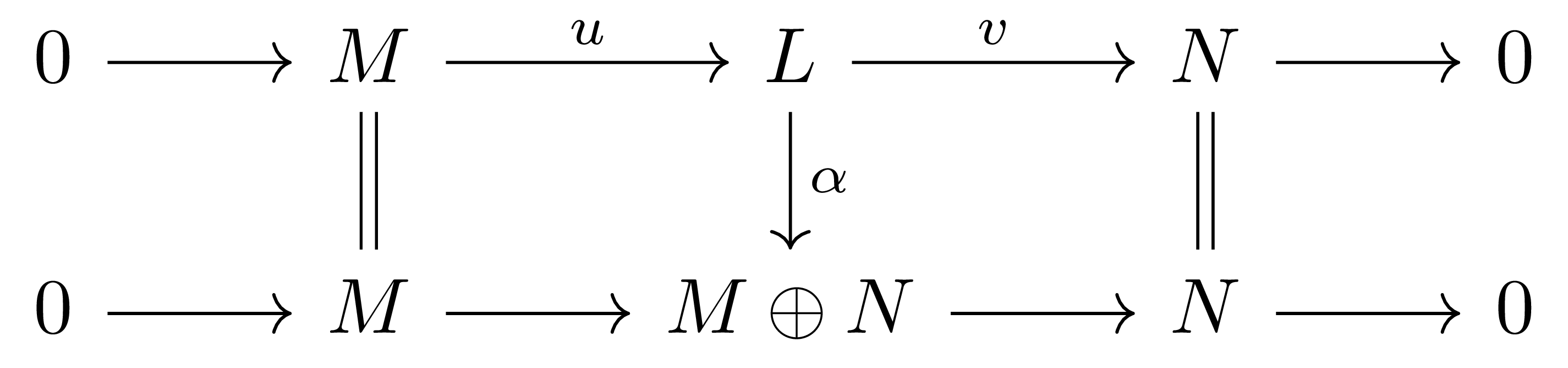
   을 commute하도록 하는 isomorphism \(\alpha: L \rightarrow M\oplus N\)이 존재한다.

증명

우선 3번 조건을 가정하자. 그럼 \(r=\pr_M\circ\alpha\)로 두면 1번 조건을 얻으며, 비슷하게 canonical inclusion \(i_N: N \rightarrow M\oplus N\)과 \(\alpha\)를 합성하여 \(s=\alpha^{-1}\circ i_N\)으로 두면 2번 조건을 얻는다.

나머지 방향은 1번과 2번 조건을 각각 가정하고 3번 조건을 보인다. 만일 1번 조건이 성립한다면 \(\beta: M\oplus N \rightarrow L\)을 \((x,y)\mapsto u(x)+s(y)\)로 정의하고, 2번 조건이 성립한다면 \(\alpha:L \rightarrow M\oplus N\)을 \(z\mapsto (r(z), v(z))\)로 정의한다. 그럼 보조정리 9에 의하여 \(\alpha,\beta^{-1}\)가 3번 조건에서 요구하는 isomorphism을 정의한다는 것을 알 수 있다.