Diagram chasing

호몰로지 대수학은 말 그대로 chain complex들이 주어졌을 때 이들의 호몰로지를 이용하여 그 성질을 살펴보는 학문이다. ([범주론] §아벨 카테고리, ⁋정의 4) Chain complex는 임의의 abelian category에서 정의되지만, Freyd-Mitchell embedding theorem에 의해 이들은 모두 적당한 \(\lMod{A}\)의 full subcategory로 embed될 수 있다. ([범주론] §아벨 카테고리, ⁋정리 9)

이번 글에서는 호몰로지 대수를 할 때 필수적인 보조정리인 5항 보조정리와 뱀 보조정리를 증명한다. 이들의 증명은 kernel과 cokernel의 universal property를 사용하여 하는 것이 가능하지만, 이는 증명을 불필요하게 길게 만들 수 있으므로 우리는 모든 증명을 \(\lMod{A}\)에서 진행한다. 이는 특히 각 대상들에서 원소를 뽑아올 수 있음을 의미한다. 이와 같은 증명을 diagram chasing이라 부르며, 임의의 abelian category 대신 \(\lMod{A}\)에서 증명을 진행하는 것은 위에서 언급한 Freyd-Mitchell embedding theorem에 의해 정당화될 수 있다.

5항 보조정리

명제 1 (The four lemma) 각 행들이 exact인 commutative diagram

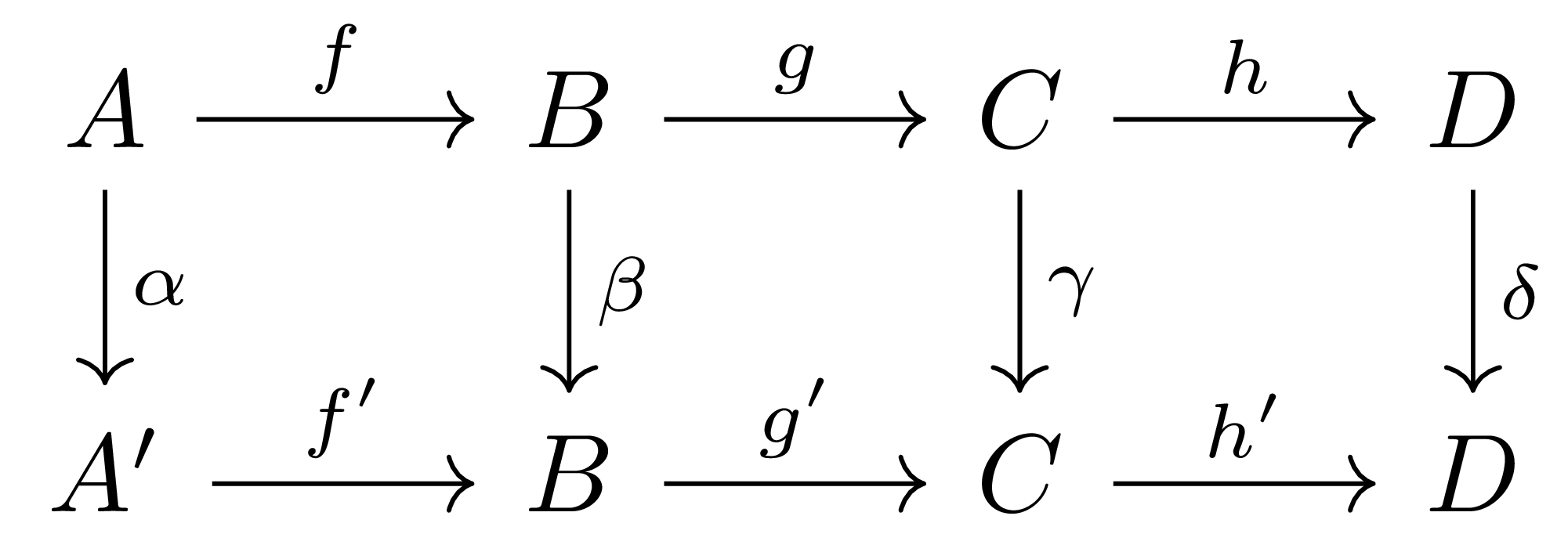
이 주어졌다 하고, \(\alpha\)가 전사이고, \(\delta\)가 단사라 가정하자. 그럼

1. 만일 \(\gamma\)가 전사라면 \(\beta\) 또한 전사이다.
2. 만일 \(\beta\)가 단사라면 \(\gamma\) 또한 단사이다.

증명

1. 임의의 \(b'\in B'\)를 택하자. 우리는 적당한 \(b\in B\)가 존재하여 \(\beta(b)=b'\)임을 보여야 한다. 가정에 의해 \(\gamma\)는 전사이므로, 적당한 \(c\in C\)가 존재하여 \(\gamma(c)=g'(b')\in C'\)가 성립한다. 이제

   \[\delta(h(c))=h'(\gamma(c))=h'(g'(b'))=0\]

   이므로 \(h(c)\in\ker\delta\)이고, \(\delta\)는 단사이므로 \(h(c)=0\)이다. 즉, \(c\in\ker(h)=\im(g)\)이므로 적당한 \(b_0\in B\)가 존재하여 \(g(b_0)=c\)이다. 이제 이러한 \(b_0\)에 대하여, \(b'-\beta(b_0)\in B'\)를 생각하자. 그럼

   \[g'(b'-\beta(b_0))=g'(b')-g'(\beta(b_0))=\gamma(c)-\gamma(g(b_0))=\gamma(c)-\gamma(c)=0\]

   이므로, \(b'-\beta(b_0)\in\ker(g')=\im(f')\)가 성립한다. 따라서 적당한 \(a'\in A'\)가 존재하여 \(f'(a')=b'-\beta(b_0)\)이다. \(\alpha\)는 전사이므로, \(\alpha(a)=a'\)를 만족하는 \(a\in A\)가 존재한다. 그럼

   \[\beta(f(a))=f'(\alpha(a))=f'(a')=b'-\beta(b_0)\]

   이고, 따라서 \(b=b_0+f(a)\)라 하면 \(\beta(b)=b'\)임을 확인할 수 있다.

2. 어떤 \(c\in C\)가 \(\gamma(c)=0\)을 만족한다 하자. 우리는 \(c=0\)임을 보여야 한다. 우선

   \[0=h'(0)=h'(\gamma(c))=\delta(h(c))\]

   이고, \(\delta\)는 단사이므로 \(h(c)=0\)임을 안다. 즉 \(c\in\ker(h)=\im(g)\)이므로, 적당한 \(b_0\in B\)가 존재하여 \(g(b_0)=c\)이다. 이제 \(B'\)의 원소 \(\beta(b_0)\)를 생각하면,

   \[g'(\beta(b_0))=\gamma(g(b_0))=\gamma(c)=0\]

   이므로, \(\beta(b_0)\in\ker(g')=\im(f')\)이 성립한다. 따라서 적당한 \(a'\in A'\)가 존재하여 \(f'(a')=\beta(b_0)\)이고, \(\alpha\)는 전사이므로 \(\alpha(a)=a'\)를 만족하는 \(a\in A\)도 존재한다. 이제 \(b=b_0-f(a)\)라 하자. 그럼

   \[g(b)=g(b_0-f(a))=g(b_0)-g(f(a))=g(b_0)=c\]

   이다. 한편,

   \[\beta(b)=\beta(b_0-f(a))=\beta(b_0)-\beta(f(a))=\beta(b_0)-f'(\alpha(a))=\beta(b_0)-f'(a')=\beta(b_0)-\beta(b_0)=0\]

   이므로 \(b\in\ker(\beta)\)이고, \(\beta\)는 단사이므로 \(b=0\)가 된다. 따라서 \(c=g(b)=0\)이고, \(\gamma\)는 단사이다.

위의 명제는 다음의 자명한 두 따름정리를 갖는다.

따름정리 2 (The five lemma) 각 행이 exact인 commutative diagram

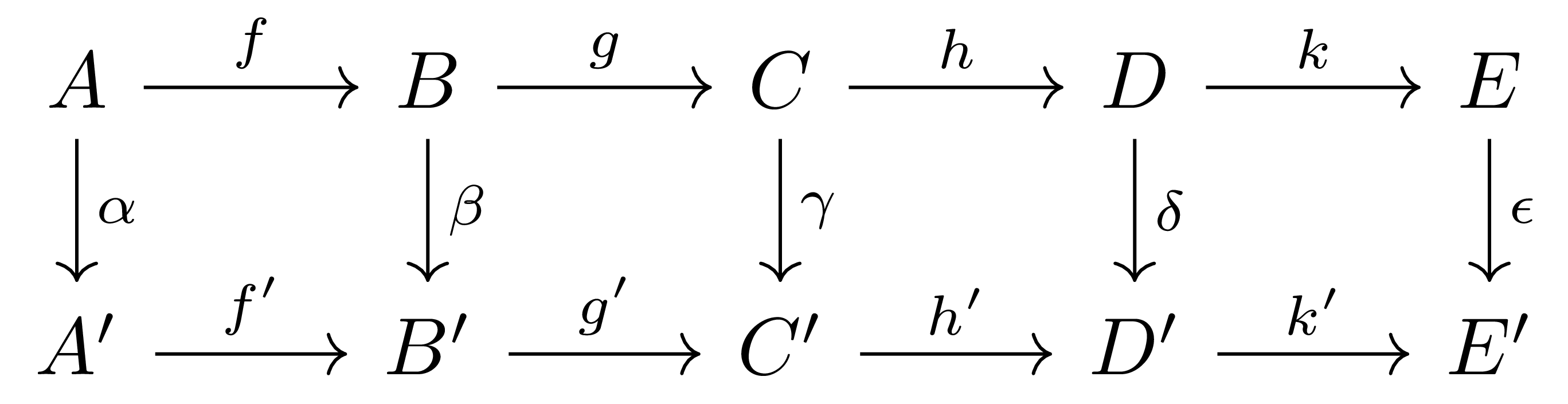
이 주어졌다 하자. 만일 \(\alpha,\beta,\delta,\epsilon\)이 모두 전단사라면, \(\gamma\) 또한 전단사이다.

따름정리 3 (The short five lemma) 각 행이 exact인 commutative diagram

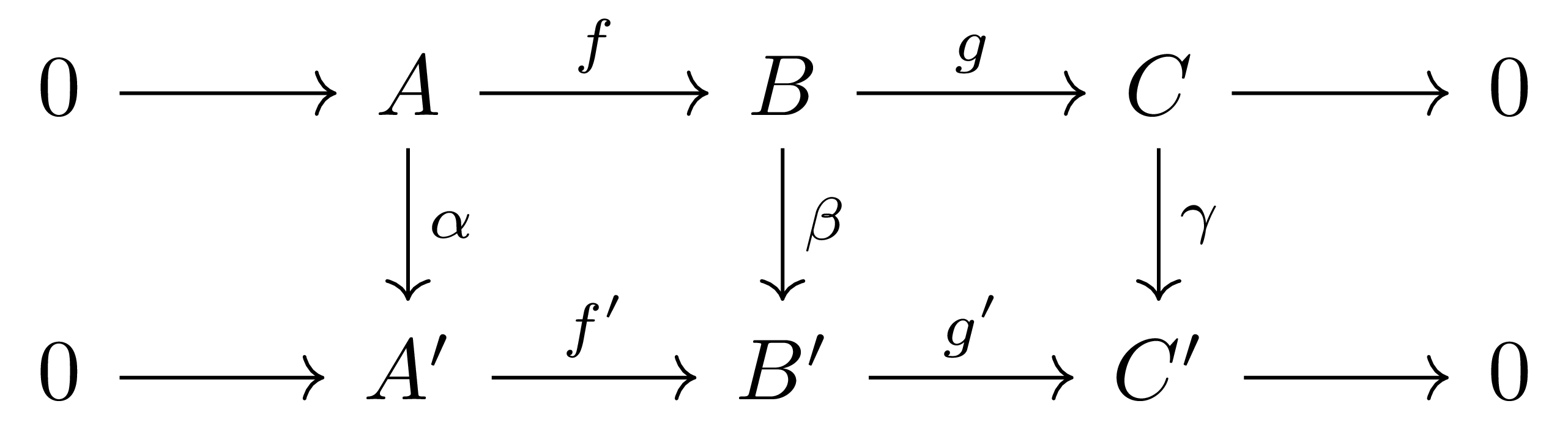
이 주어졌다 하자. 만일 \(\alpha,\gamma\)가 모두 단사라면 \(\beta\)도 단사이고, \(\alpha,\gamma\)가 모두 전사라면 \(\beta\)도 전사이다.

뱀 보조정리

남은 글에서 우리의 주된 목표는 뱀 보조정리를 증명하는 것인데, 이를 위해서는 두 개의 보조정리가 필요하다.

보조정리 4 Commutative square

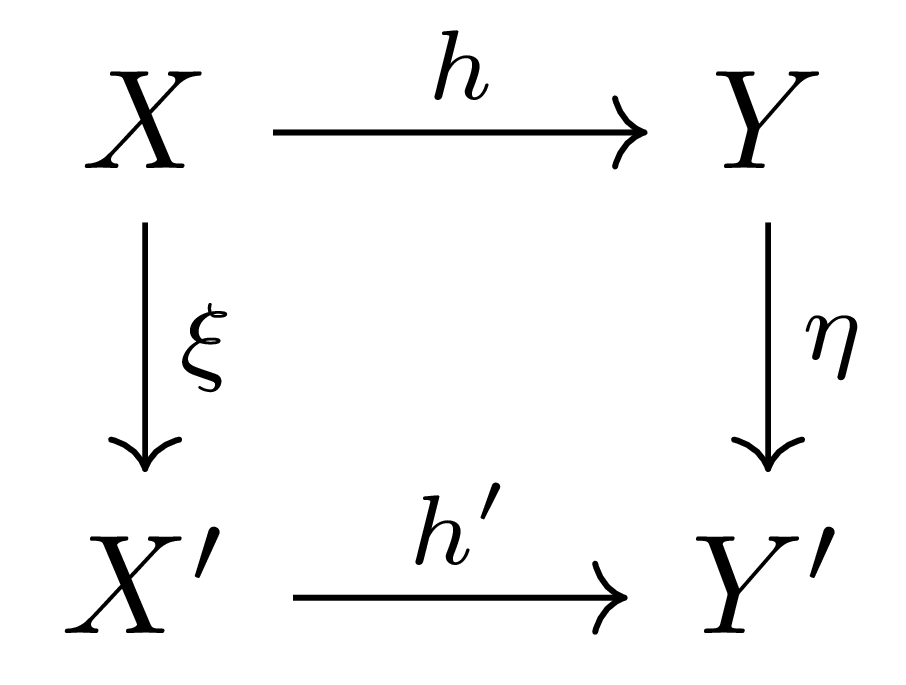
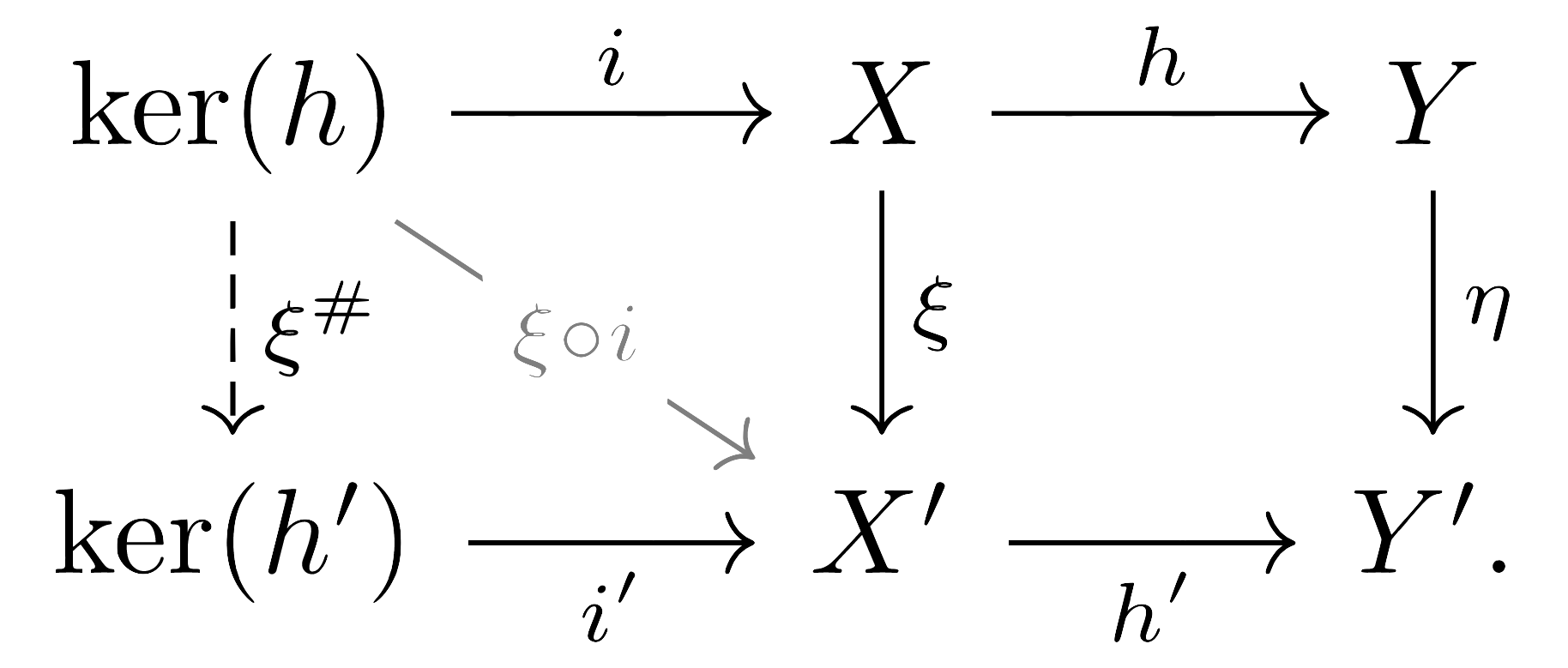
가 주어졌다 하자. 그럼 \(\xi\)는 \(\ker(h)\)를 \(\ker(h')\)로, \(\eta\)는 \(\im(h)\)를 \(\im(h')\)로 보내며, 특히 다음의 함수들

\[\xi^\sharp:\ker(h)\rightarrow\ker(h'),\quad \eta^\sharp:\im(h)\rightarrow\im(h'),\quad\xi^\ast:X/\ker(h)\rightarrow X'/\ker(h'),\quad \eta^\ast:\coker(h)\rightarrow\coker(h')\]

이 잘 정의된다.

증명

\(i:\ker(h)\rightarrow X\)와 \(\xi\)의 합성 \(\xi\circ i:\ker h\rightarrow X'\)를 생각하자. 그럼

\[h'\circ(\xi\circ i)=(\eta\circ h)\circ i=\eta\circ 0=0\]

이므로, kernel의 universal property로부터 유일한 \(\xi^\sharp:\ker(h)\rightarrow\ker(h')\)가 존재한다는 것을 안다.

비슷하게 \(p'\circ\eta:Y\rightarrow \coker (h')\)로부터,

\[(p'\circ\eta)\circ h=p'\circ(h'\circ\xi)=(p'\circ h')\circ\xi=0\circ\xi=0\]

이고, \(\coker(h)\)의 universal property로부터 \(\eta^\ast\)를 정의할 수 있다.

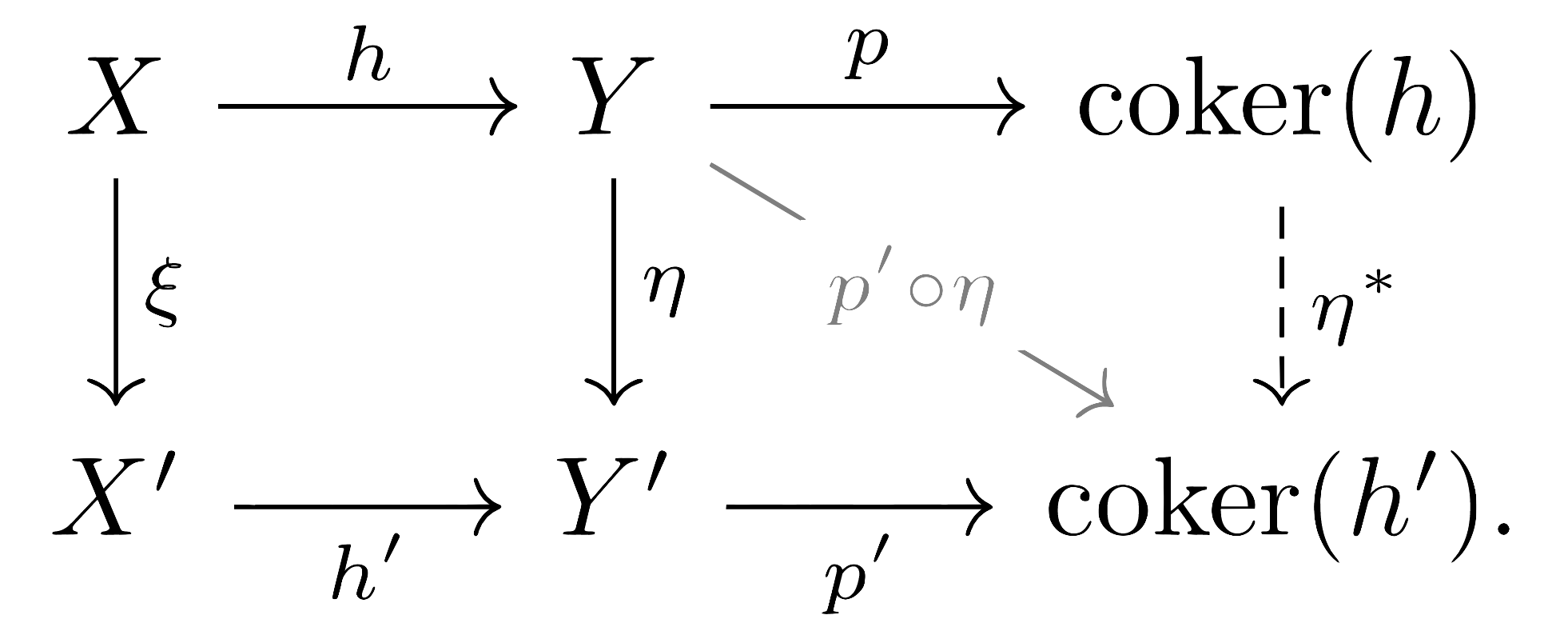
정의에 의해 \(\coker(h)=Y/\im(h), \coker(h')=Y'/\im(h')\)이므로, \(\eta^\ast\)가 \(0\)을 \(0\)으로 보내는 것으로부터 \(\eta^\sharp\) 또한 잘 정의된다. 마지막으로 \(\xi^\ast\)의 경우, \(p:X'\rightarrow X'/\ker(h')\)를 생각하면

\[\ker(h)\subseteq\ker(p\circ\xi)\]

이고, 따라서 \(p\circ\xi\)가 \(\xi^\ast:X/\ker(h)\rightarrow X'/\ker(h')\)를 유도한다.

이를 이용하면 다음 보조정리를 보일 수 있다.

보조정리 5 각 행이 exact인 commutative diagram

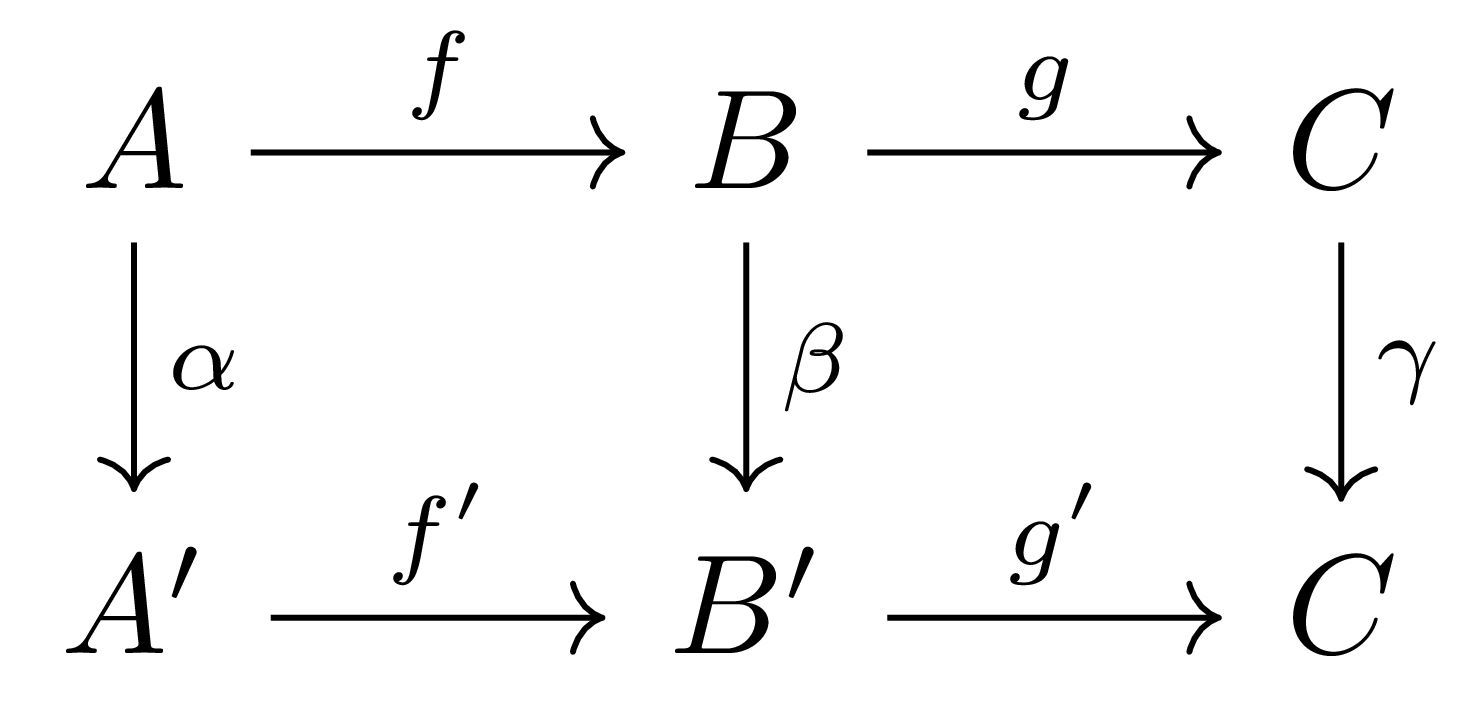
이 주어졌다 하자. 그럼 \(f,g\)와 \(f',g'\)는 각각 다음의 두 열

\[\ker(\alpha)\rightarrow\ker(\beta)\rightarrow\ker(\gamma),\qquad \coker(\alpha)\rightarrow\coker(\beta)\rightarrow\coker(\gamma)\]

를 유도한다. 뿐만 아니라, \(f':A'\rightarrow B'\)가 단사라면 첫째 열이 exact가 되고, \(g:B\rightarrow C\)가 전사라면 둘째 열이 exact가 된다.

증명

\(f,g\)와 \(f',g'\)이 각각 주어진 두 개의 열

\[\ker(\alpha)\overset{f^\sharp}{\longrightarrow}\ker(\beta)\overset{g^\sharp}{\longrightarrow}\ker(\gamma),\qquad \coker(\alpha)\overset{(f')^\ast}{\longrightarrow}\coker(\beta)\overset{(g')^\ast}{\longrightarrow}\coker(\gamma)\]

을 유도하는 것은 보조정리 4의 결과이다. 뿐만 아니라, \(i_A, i_B, i_C\)를 각각 kernel들에서 \(A,B,C\)로의 자명한 함수들이라 하면

\[i_C\circ g^\sharp\circ f^\sharp=g\circ i_B\circ f^\sharp=g\circ f\circ i_A=0\]

이고, \(i_C\)가 단사인 것으로부터 \(g^\sharp\circ f^\sharp=0\)임을 확인할 수 있다. 비슷하게 \(p_A,p_B,p_C\)를 각각 \(A,B,C\)에서 cokernel들로의 자명한 함수들이라 하면,

\[(g')^\ast\circ(f')^\ast\circ p_C=(g')^\ast\circ p_B\circ f=p_A\circ g'\circ f'=0\]

이고, \(p_C\)가 전사인 것으로부터 \((g')^\ast\circ(f')^\ast=0\)임을 확인할 수 있다. 따라서 주어진 명제를 보이기 위해서는 \(f':A'\rightarrow B'\)가 단사라면 \(\ker(g^\sharp)\subset\im(f^\sharp)\)이고, \(g:B\rightarrow C\)가 전사라면 \(\ker((g')^\ast)\subset\im((f')^\ast)\)임을 보이면 충분하다.

우선 \(f'\)가 단사라고 가정하자. 만일 어떤 \(b\in\ker(\beta)\)에 대하여 \(g^\sharp(b)=0\)이라면, \(g^\sharp\)의 정의에 의해 \(g(b)=0\)이고 따라서 \(b\in\ker(g)=\im(f)\)이다. 따라서 어떤 \(a\in A\)가 존재하여 \(f(a)=b\)가 성립한다. 그런데

\[(f'\circ\alpha)(a)=(\beta\circ f)(a)=\beta(f(a))=\beta(b)=0\]

에서, \(f'\)는 단사이므로 \(a\in\ker(\alpha)\)이고 \(f(a)=f^\sharp(a)=b\)로부터 \(b\in\im(f^\sharp)\)이 된다.

이제 \(g\)가 전사라고 가정하자. \(b'\in\coker(\beta)\)가 \(\ker((g')^\ast)\)의 원소라 하자. 즉 \(((g')^\ast)(b')=g'(b')+\im(\gamma)=0\)이다. 그런데 \(g'(b')\in\im(\gamma)\)이므로, 적당한 \(c\in C\)가 존재하여 \(\gamma(c)=g'(b')\)이고, \(g\)는 전사이므로 적당한 \(b\in B\)가 존재하여 \(g(b)=c\)이다. 이 때

\[g'(b')=\gamma(c)=(\gamma\circ g)(b)=(g'\circ\beta)(b)\]

이므로, \(b'-\beta(b)\in\ker(g')=\im(f')\)가 성립한다. 이제 \(f'(a')=b'-\beta(b)\)를 만족하는 \(a'\in A'\)를 택하자. 그럼 \(f'(a')-b'\in\im(\beta)\)이므로,

\[f'(a')+\im(\beta)=b'+\im(\beta)\]

이고 따라서

\[((f')^\ast)(a'+\im(\alpha))=b'+\im(\beta)\]

이 성립한다.

이제 드디어 snake lemma를 증명할 수 있다.

정리 6 (The snake lemma) 각 행이 exact인 commutative diagram

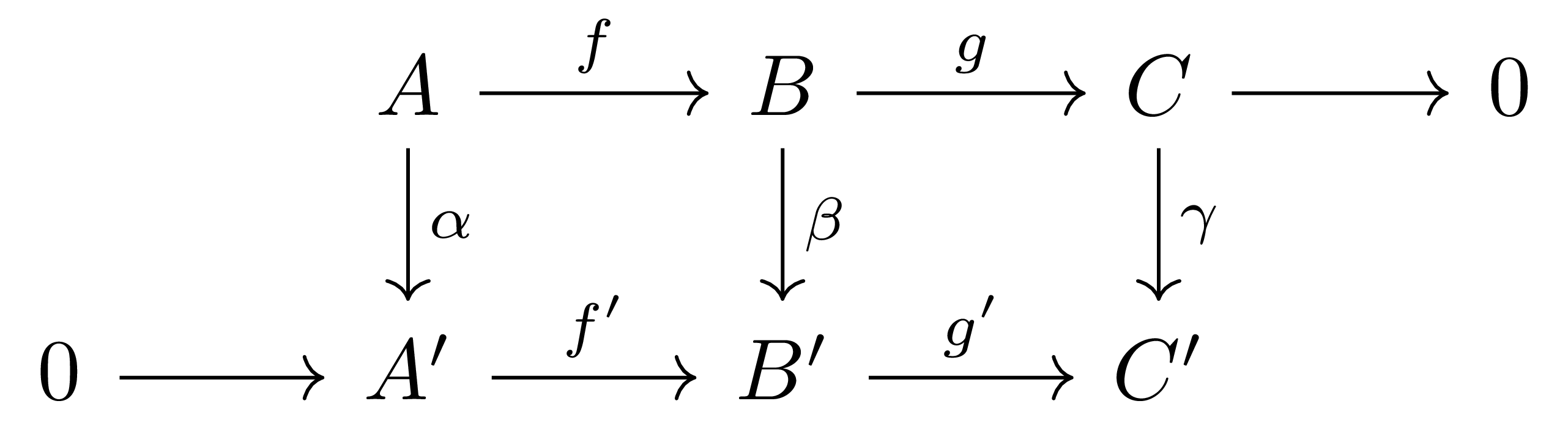
이 주어졌다 하자. 이 때, 위와 아래의 행은 각각 exact이다. 그럼 보조정리 5에서부터 얻어진 두 개의 exact sequence

\[\ker(\alpha)\rightarrow\ker(\beta)\rightarrow\ker(\gamma),\qquad \coker(\alpha)\rightarrow\coker(\beta)\rightarrow\coker(\gamma)\]

를 잇는 \(\delta:\ker(\gamma)\rightarrow\coker(\alpha)\)가 존재하여, 이를 통해 이어진 다음의 열

\[\ker(\alpha)\rightarrow\ker(\beta)\rightarrow\ker(\gamma)\rightarrow\coker(\alpha)\rightarrow\coker(\beta)\rightarrow\coker(\gamma)\]

이 exact sequence를 이룬다.

증명

증명을 위해서는 \(\delta\)를 하나 만들고, 이후 위의 열이 \(\ker(\gamma)\)와 \(\coker(\alpha)\)에서 각각 exact임을 보이면 충분하다.

우선 \(c\in\ker(\gamma)\)를 하나 택하자. 그럼 \(g\)가 전사이므로, 적당한 \(b\in B\)가 존재하여 \(g(b)=c\)가 성립하며, 이 \(b\)는 다음의 식

\[0=\gamma(c)=\gamma(g(b))=(\gamma\circ g)(b)=(g'\circ\beta)(b)=g'(\beta(b))\]

을 만족한다. 즉 \(\beta(b)\in\ker(g')=\im(f')\)이다. 따라서 \(f'(a')=\beta(b)\)이도록 하는 \(a'\)가 유일하게 존재한다. 이러한 \(a'\)에 대하여 \(\delta(c)=a'+\im(\alpha)\in \coker(\alpha)\)라 하자.

함수 \(delta\)가 잘 정의되기 위해서는 위의 함수값이 \(b\)의 선택에 의존하지 않아야 한다. \(g(b_1)=c\)를 만족하는 또다른 \(b_1\in B\)를 택하고, 위와 같은 방식으로 \(f'(a_1')=\beta(b_1)\)을 만족하는 \(a_1'\in A'\)를 택하자. 그럼

\[0=(g'\circ f')(a_1'-a_1)=(g'\circ \beta)(b_1-b)=(\gamma\circ g)(b_1-b)\]

이므로 \(b_1-b\in\ker(g)=\im(f)\)이 성립한다. 이제 \(f(a)=b_1-b\)이도록 하는 \(a\in A\)를 찾으면,

\[f'(\alpha(a))=\beta(f(a))=\beta(b_1)-\beta(b)=f'(a_1'-a')\]

이고, \(f'\)가 단사이므로 \(\alpha(a)=a_1'-a'\)가 성립한다. 즉, \(a_1'\equiv a' \mod \im(\alpha)\)이고, \(\delta\)가 잘 정의된다. 어렵지 않게 \(\delta\)가 \(A\)-module들 사이의 homomorphism임을 보일 수 있다.

이렇게 만든 \(\delta\)가 다음의 열

\[\ker(\beta)\rightarrow\ker(\gamma)\rightarrow\coker(\alpha)\rightarrow\coker(\beta)\]

을 exact sequence로 만든다는 것을 보여야 한다. 우선 \(b\in \ker(\beta)\)라 하자. \(\delta(g^\sharp(b))=a'+\im(\alpha)\)라 하면 \(a'\)는 식 \(f'(a')=\beta(b)\)에 의하여 결정되는데, \(b\in\ker(\beta)\)이므로 \(f'(a')=0\)이고, \(f'\)는 단사이므로 \(a'=0\)이어야 한다. 즉 \(\delta\circ g^\sharp=0\)이다. 이와 비슷하게, 임의의 \(c\in\ker(\gamma)\)에 대하여 \(\delta(c)=a'+\im(\alpha)\)라 하면,

\[((f')^\ast)(a'+\im(\alpha))=f'(a')+\im(\beta)=\beta(b)+\im(\beta)=0\]

가 된다. 따라서 \(\ker(\delta)\subset\im(g^\sharp)\)이고 \(\ker(f')^\ast\subset\im(\delta)\)이라는 것만 보이면 충분하다.

우선 \(c\in\ker(\delta)\)라 하자. 그럼 \(a'\)는 \(g(b)=c\)를 만족하는 \(b\)에 대해, 식 \(f'(a')=\beta(b)\)를 만족하는 원소로 정의되므로 \(a'\in\im(\alpha)\)이다. 이제 \(\alpha(a)=a'\)를 만족하는 \(a\in A\)를 택하자. 그럼

\[\beta(b)=f'(a')=f'(\alpha(a))=\beta(f(a))\]

이므로 \(b-f(a)\in\ker(\beta)\)이다. 이제

\[g^\sharp(b-f(a))=g(b-f(a))=g(b)-g(f(a))=g(b)=c\]

이므로 \(c\in\im g^\sharp\)가 성립한다.

비슷하게 \(a'\in\ker(f')^\ast\)라 하자. 그럼 \(f'(a')\in\im(\beta)\)이므로 적당한 \(b\in B\)가 존재하여 \(\beta(b)=f'(a')\)가 성립하고, 이 \(b\)에 대하여

\[\gamma(g(b))=(g'\circ\beta)(b)=(g'\circ f')(a')=0\]

가 성립하므로 \(g(b)\in\ker(\gamma)\)이다. 따라서 \(\delta(g(b))\)가 잘 정의되며, \(b\)가 정확히 \(f'(a')=\beta(b)\)를 만족하는 원소로 정의되었으므로 이 값은 정확히 \(a'+\im(\alpha)\)와 같다.

이 정리를 snake lemma라고 부르는 것은 connecting map \(\delta\)를 그렸을 때, 다음과 같은 모양이 나오기 때문이다.

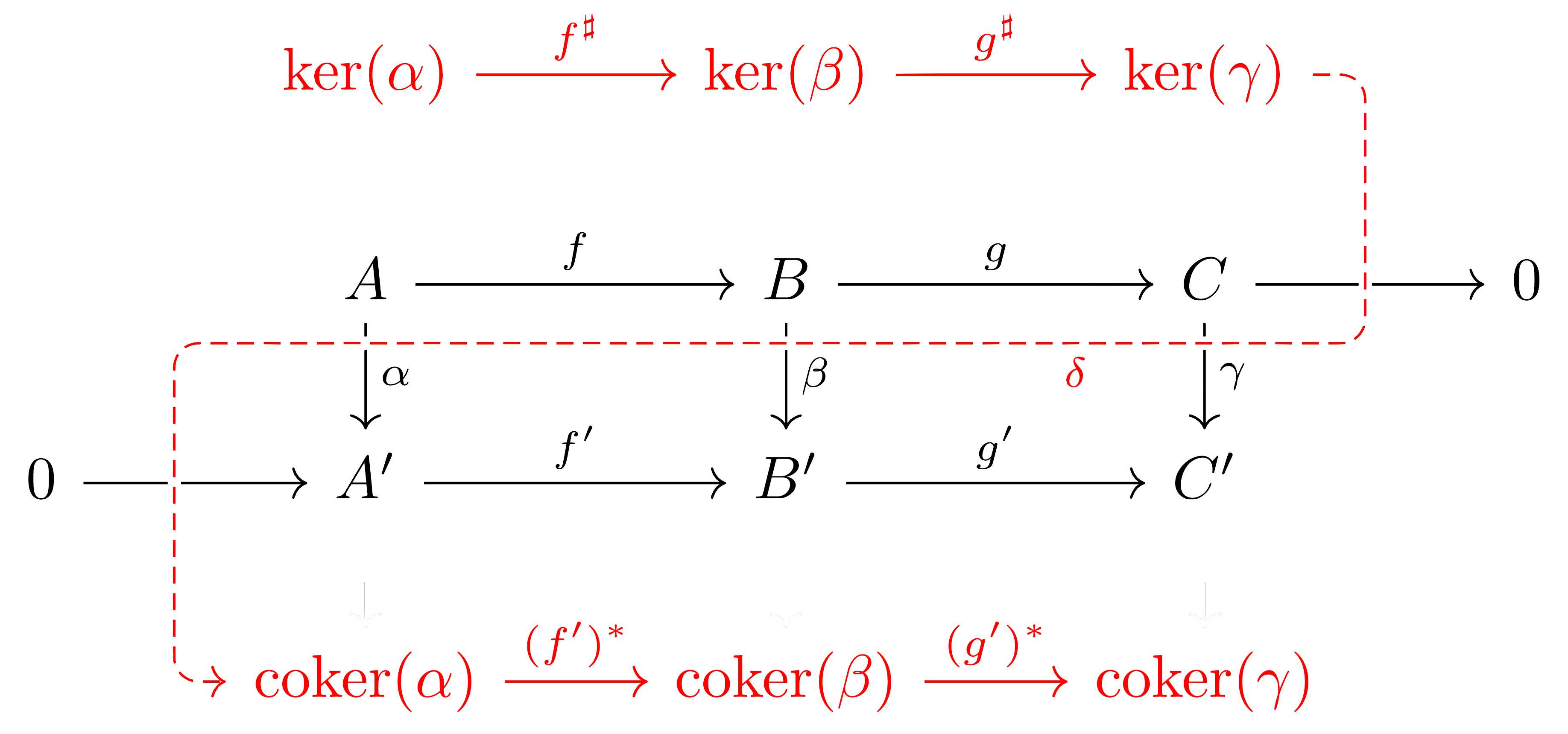
Snake lemma는 보통 다음 글에서와 같이 long exact sequence를 그릴 때 사용되지만, 다음의 또 다른 따름정리 또한 갖는다.

따름정리 7 (The 3×3 lemma) 각 행이 exact인 commutative diagram

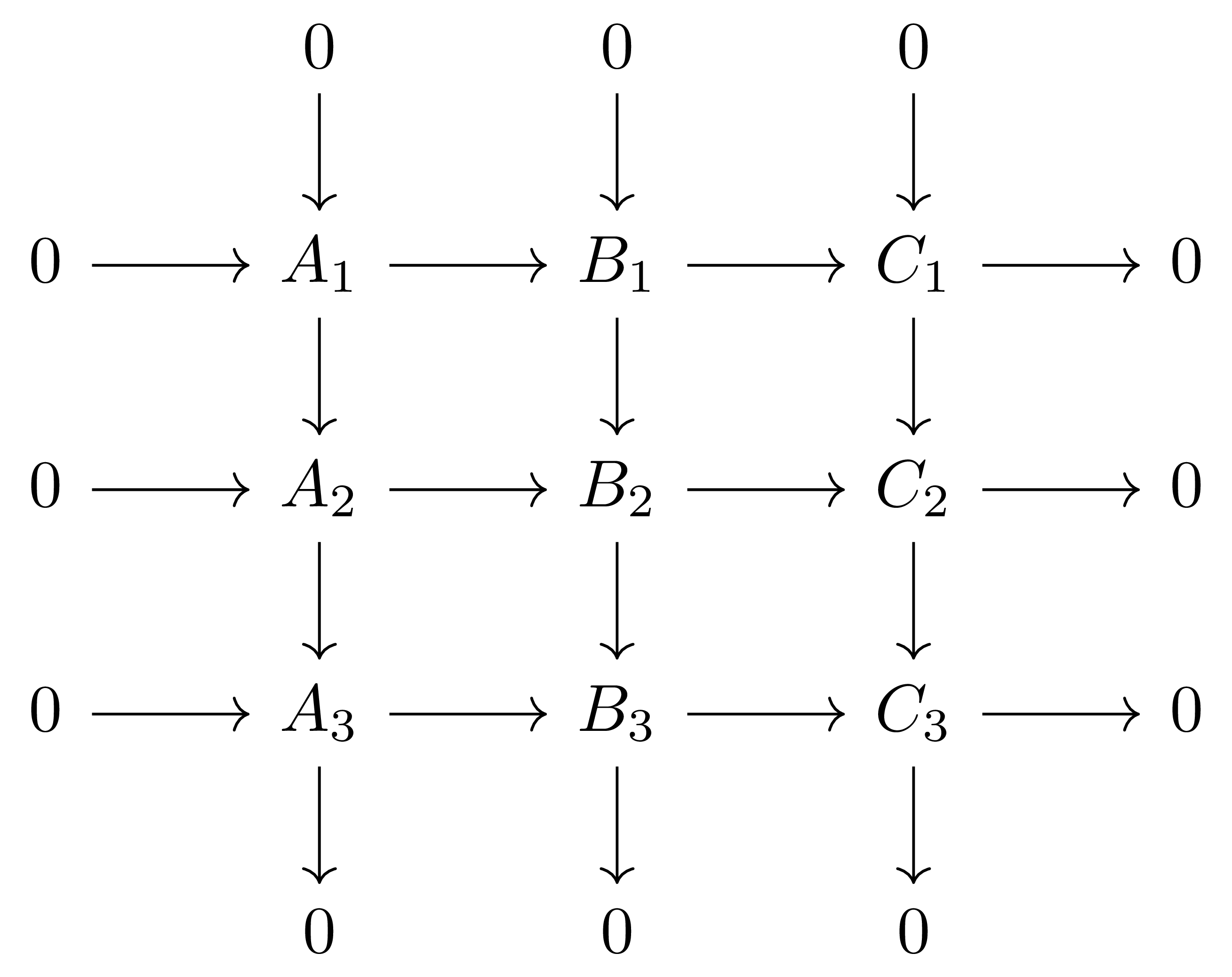
이 주어졌다 하자. 만일 첫 두 개의 열이 모두 short exact sequence라면 마지막 열 또한 short exact sequence가 되고, 마지막 두 개의 열이 모두 short exact sequence라면 첫 열 또한 short exact sequence가 된다.

---

참고문헌

[Hu] S.T. Hu, Introduction to homological algebra. University Microfilms, 1979.