미분

이번 글에서의 목표는 대수적으로 미분을 정의하는 것이다.

캘러미분가군

정의 1 Ring \(A\)와 \(A\)-algebra \(E\), 그리고 \(E\)-module \(M\)이 주어졌다 하자. 그럼 다음의 Leibniz rule

\[d(xy)=y\,dx+x\,dy\]

을 모든 \(x,y\in E\)에 대해 만족하는 \(A\)-linear map들을 \(A\)-derivation이라 부르고 이들의 모임을 \(\Der_A(E,M)\)으로 적는다.

Derivation의 기본적인 성질 중 하나는 \(\Der_A(E,M)\)이 \(E\)-module 구조를 갖는다는 것으로, 이는 임의의 \(x\in E\)와 \(d\in \Der_A(E, M)\)에 대하여, \(A\)-linear map \(x d\)를 다음의 식

\[xd: E \rightarrow M;\qquad y\mapsto x\,d(y)\]

으로 정의하면 임의의 \(y_1,y_2\in E\)에 대하여 다음 식

\[(xd)(y_1y_2)=x\,d(y_1y_2)=x\, (y_1\,dy_2+y_2\,dy_1)=y_1(xd)(y_2)+y_2(xd)(y_1)\]

이 성립하기 때문이다. 뿐만 아니라 임의의 \(A\)-derivation \(d: E \rightarrow M\)과 임의의 \(E\)-linear map \(u:M \rightarrow M'\)이 주어졌을 때, 합성

\[u\circ d: E \rightarrow M'\]

또한 \(A\)-derivation이 되는 것을 확인할 수 있는데, 이는 다음 식

\[(u\circ d)(y_1y_2)=u(y_1\,dy_2+y_2\,dy_1)=y_1u(dy_2)+y_2u(dy_1)=y_1(u\circ d)(y_2)+y_2(u\circ d)(y_1)\]

에 따른 것이다. 즉, \(\Der_A(E, -)\)는 \(\lMod{E}\)에서 자기자신으로의 functor가 된다.

보조정리 2 Functor \(\Der_A(E, -)\)는 representable하다. 즉, \(\lMod{E}\)에서 자기자신으로의 두 functor들 사이의 natural isomorphism

\[\Der_A(E,-)\cong\Hom_E(\Omega_{E/A},-)\]

이 성립하도록 하는 \(E\)-module \(\Omega_{E/A}\)이 존재한다.

Representing object \(\Omega_{E/A}\)는 다음과 같이 정의된다.

정의 3 \(A\)-algebra \(E\)에 대하여, \(E\)의 \(A\)에 대한 Kähler differential module_{캘러 미분가군}은 \(\{df\mid f\in E\}\)로 생성되는 \(E\)-module에, 다음의 relation들

\[\text{$d(xy)=x\,dy+y\,dx$ for all $x,y\in E$},\qquad \text{$d(ax+by)=a\,dx+b\,dy$ for all $x,y\in E$ and $a,b\in A$}\]

을 주어 만들어지는 \(E\)-module이며, 이를 \(\Omega_{E/A}\)로 표기한다. 이 때, \(f\mapsto df\)로 정의되는 \(A\)-linear derivation \(d:E \rightarrow \Omega_{E/A}\)를 universal \(A\)-derivation이라 적는다.

그럼 \(\Omega_{E/A}\)가 원하는 universal property (보조정리 2)를 만족하는 것을 쉽게 확인할 수 있다. 뿐만 아니라, \(\Omega_{E/A}\)를 \(A\)-algebra \(A \rightarrow E\)를 받아 \(\Omega_{E/A}\)를 내놓는 functor처럼 생각하면, 다음과 같은 종류의 functoriality 또한 성립한다.

명제 4 다음의 ring homomorphism들의 commutative diagram

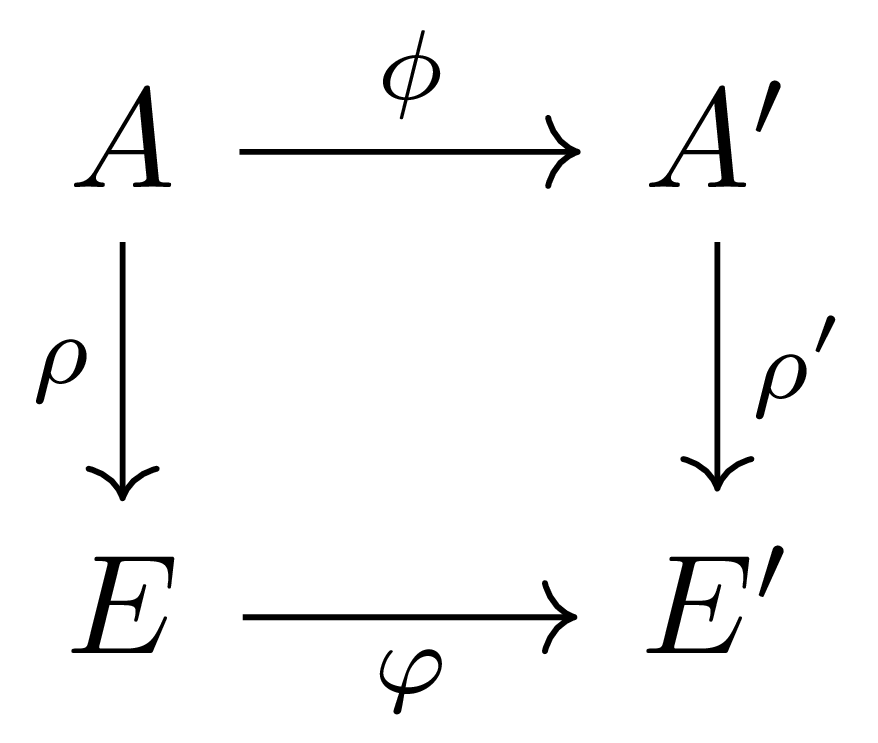
이 주어졌다 하고, \(\rho\)와 \(\rho'\)를 통해 \(E, E'\)를 각각 \(A\)-algebra와 \(A'\)-algebra로 보자. 그럼 다음의 diagram

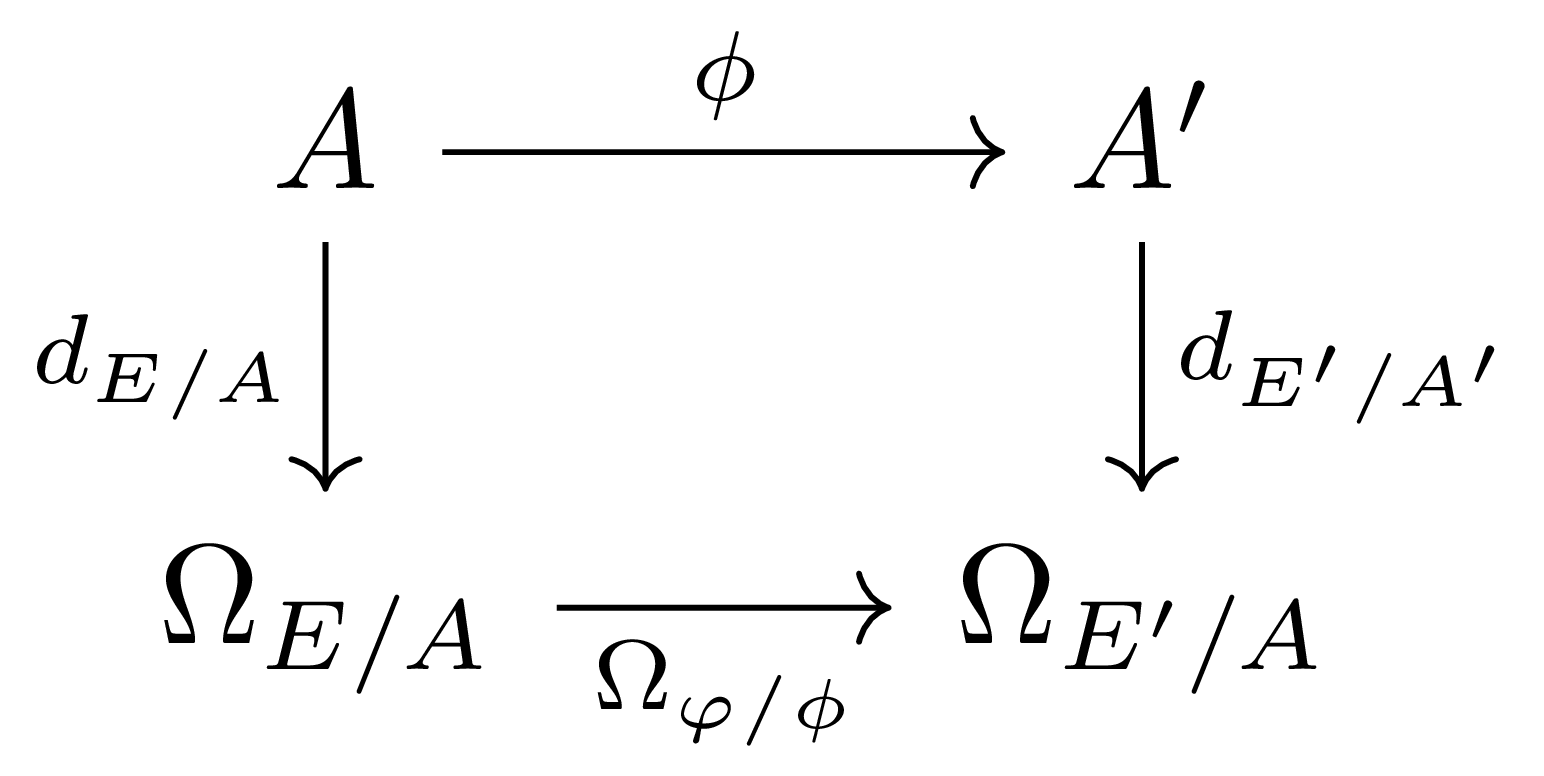
을 commute하게 하는 유일한 \(E\)-linear map \(\Omega_{\varphi/\phi}:\Omega_{E/A} \rightarrow \Omega_{E'/A'}\)이 존재한다.

증명

\(d_{E'/A'}\circ \phi\)가 \(A\)-derivation이므로 보조정리 2에 의해 자명하다.

한편 \(\Omega_{E'/A'}\)는 \(E'\)-module이므로, [대수적 구조] §스칼라의 변환, ⁋명제 5에 의하여

\[\Hom_{E'}(\varphi_! \Omega_{E/A},\Omega_{E'/A'})\cong\Hom_E(\Omega_{E/A}, \varphi^\ast\Omega_{E'/A'})\]

이 성립한다. 그럼 위의 명제 4에서 얻어지는 \(\Omega_{E/A} \rightarrow \Omega_{E'/A'}\)는 엄밀히 이야기하자면 \(\Omega_{E/A} \rightarrow \varphi^\ast\Omega_{E'/A'}\)이므로, 이에 해당하는 유일한 \(E'\)-linear homomorphism

\[\Omega_{\varphi/\phi}': \varphi_!\Omega_{E/A}=\Omega_{E/A}\otimes_EE' \rightarrow \Omega_{E'/A'}\]

이 존재한다.

Fundamental sequences

특별히 \(\phi:A \rightarrow A'\)를 \(\id_A:A \rightarrow A\)로 두자. 그럼 위에서 만든 \(E'\)-linear homomorphism은 오직 \(A\)-linear map \(\varphi:E \rightarrow E'\)에만 의존하며, 다음의 꼴

\[\Omega_{\varphi/A}':\Omega_{E/A}\otimes_EE' \rightarrow \Omega_{E'/A}\]

이 된다. 한편, \(\varphi:E \rightarrow E'\)를 통해 \(E'\)를 \(E\)-algebra로 보면 \(E'\)의 \(E\)에 대한 Kähler differential module \(\Omega_{E'/E}\)가 정의되며, 이 때 universal \(E\)-derivation \(d_{E'/E}: E \rightarrow \Omega_{E'/E}\)는 \(A\)-derivation이기도 하므로 다시 보조정리 2에 의하여 다음 식

\[d_{E'/E}=E' \overset{d_{E'/A}}{\longrightarrow}\Omega_{E'/A}\overset{\Omega_\varphi}{\longrightarrow}\Omega_{E'/E}\]

과 동일하다.

명제 5 (Cotangent sequence) \(E'\)-linear map들의 sequence

\[\Omega_{E/A}\otimes_EE'\overset{\Omega_{\varphi/A}'}{\longrightarrow}\Omega_{E'/A}\overset{\Omega_\varphi}{\longrightarrow}\Omega_{E'/E} \longrightarrow 0\]

는 exact이다.

증명

또 다른 중요한 exact sequence는 특별히 \(\varphi:E \rightarrow E'\)가 surjective인 경우에 얻어진다. 이 경우, first isomorphism theorme에 의하여

\[E/\ker \varphi\cong E'\]

가 성립한다. 편의상 \(K=\ker\varphi\)라 적자. 그럼 \(d_{E/A}:E \rightarrow \Omega_{E/A}\)를 \(K\)로 제한한

\[d_{E/A}\vert_K: K \rightarrow \Omega_{E/A}\]

를 생각하고, 다음의 \(E\)-linear map

\[K\overset{d\vert_K}{\longrightarrow}\Omega_{E/A}\overset{}{\longrightarrow}\Omega_{E/A}\otimes_EE'\]

을 생각할 수 있다. 그럼 위의 합성의 kernel이 \(K^2\)를 포함한다는 것을 확인할 수 있고, 따라서 이로부터 \(E\)-linear map

\[\bar{d}:K/K^2 \rightarrow \Omega_{E/A}\otimes_EE'\]

을 얻는다.

명제 6 위와 같은 상황에서, 다음의 sequence

\[K/K^2 \overset{\bar{d}}{\longrightarrow}\Omega_{E/A}\otimes_EE' \rightarrow\Omega_{E'/A} \longrightarrow 0\]

는 exact이다.