위상공간 위에 정의된 sheaf의 예시 중 가장 기본적인 것은 위상공간 위에 정의된 연속함수들의 모임이며, 우리가 정의할 $\mathscr{O}_{\Spec A}$ 또한 비슷하다. 그러나 $\mathscr{O}_{\Spec A}$가 $\Spec A$ 위에 정의된 연속함수들의 sheaf였다면 여기에 굳이 새로운 이름을 붙일 필요가 없을 것이다. 가장 간단한 예시로, 임의의 field $\mathbb{K}$의 유일한 prime ideal은 $(0)$이므로, 위상공간으로서 $\Spec \mathbb{K}$는 항상 singleton일 것이며 이 위에 위상구조를 주는 방법은 하나 뿐이다. 바꾸어 말하자면, isomorphic하지 않은 두 field의 스펙트럼을 서로 구별하고자 한다면 그 정보는 $\Spec \mathbb{K}$의 structure sheaf에 들어있어야 한다. 스펙트럼이 충분히 많은 대수적인 정보를 갖도록 하기 위해, 우리는 $\mathscr{O}_{\Spec A}$를 $A$ 위에서 정의된 대수적인 함수들의 sheaf로 정의할 것이다.
Locally ringed space
기본적으로 위상공간 위에 정의된 sheaf에 대해서는 [위상수학] §층에서 이미 다루었지만, $\Spec A$에 정의할 structure sheaf를 서술하기에는 해당 글의 정의는 불충분하다.
정의 1 위상공간 $X$와, 그 위에 정의된 $\cRing$-valued sheaf $\mathscr{O}_X$의 pair $(X,\mathscr{O}_X)$를 ringed space환 달린 공간라 부른다. 만일 $X$의 임의의 점 $x$에 대하여, $x$에서의 stalk $\mathscr{O}_{X,x}$가 항상 local ring이라면 이 pair $(X, \mathscr{O}_X)$를 locally ringed space국소적 환 달린 공간라 부른다.
우리의 주장은 $\Spec A$에 적당한 structure sheaf $\mathscr{O}_{\Spec A}$를 정의하여 $(\Spec A, \mathscr{O}_{\Spec A})$를 locally ringed space로 만들 수 있고, 이렇게 정의된 $\Spec$은 §스펙트럼, ⁋명제 2 혹은 §스펙트럼, ⁋명제 8과 같은 functoriality를 갖는다는 것이다. 이를 수학적으로 적기 위해서는 우선 locally ringed space들 사이의 morphism을 정의해야 한다.
정의 2 두 ringed space $(X, \mathscr{O}_X)$, $(Y, \mathscr{O}_Y)$에 대하여, 이들 사이의 morphism은 연속함수 $\varphi:X \rightarrow Y$와 $\Sh(Y,\cRing)$에서의 morphism $\varphi^\sharp:\mathscr{O}_Y \rightarrow \varphi_\ast \mathscr{O}_X$의 pair를 의미한다.
두 locally ringed space $(X, \mathscr{O}_X)$, $(Y, \mathscr{O}_Y)$ 사이의 morphism은 ringed space로서의 morphism $(\varphi,\varphi^\sharp)$이, 추가적으로 각각의 $x\in X$에 대하여 local homomorphism $\varphi_x^\sharp:\mathscr{O}_{Y,\varphi(x)} \rightarrow \mathscr{O}_{X,x}$를 유도하는 것이다.
$\Spec A$ 위에 정의된 대수적인 함수들
이제 $\mathscr{O}_{\Spec A}$를 정의해야 한다. 이는 이 글의 서두에서 언급한 것과 같이, $\Spec A$ 위에 정의된 대수적인 함수들의 sheaf이며, 우리는 §스펙트럼, §§고전적인 대수기하학에서 $A=\mathbb{K}[\x_1,\ldots, \x_n]$일 경우 이들은 적당한 근방을 잡아 유리함수의 꼴로 나타낼 수 있는 함수임을 살펴보았다. 이 과정에서 중요한 역할을 한 것은 $A$의 원소, 즉 다항식을 $\mathbb{A}_\mathbb{K}^n=\mSpec A$ 위에서의 함수로 취급할 수 있다는 것이었는데, 일반적인 경우에는 $A$의 원소는 다항식도 아니고, 또 $\Spec A$의 점들을 $A$의 원소에 대입할 수도 없다.
따라서 이 논의를 일반화하기 위해 다음과 같이 생각하자. 우선 $A$의 원소는 앞선 예시와 마찬가지로 함수 $f$로 생각한다. 그럼 이 때 $f$의 점 $\mathfrak{p}\in\Spec A$에서의
이다. 즉 $Z(f)$는 $f=0$인 점들의 모임으로 이해할 수 있으며, 그 여집합인 principal open set $D(f)$는 $f\neq 0$인 점들의 모임으로 이해할 수 있다.
이러한 관점에서 우리는 $\Spec A$의
이제 principal open set $D(f)$가 주어졌다 하자. 그럼 정의에 의해, $D(f)$ 위의 대수적인 함수를 유리함수 $g/h$의 형태로 나타냈을 때, 그 분모에 들어갈 수 있는 함수 $h$들은 $D(f)\subseteq D(h)$를 만족해야 한다.
보조정리 3 고정된 원소 $f\in A$에 대하여,
\[S(f)=\{h\in A\mid D(f)\subseteq D(h)\}\]으로 정의하자. 그럼 $S(f)$는 $A$의 multiplicative subset이다.
증명
우선 $D(1)=\Spec A$이므로 $S(f)$가 empty product $1$을 포함하는 것은 자명하다. 이제 만일 $h_1,h_2\in S(f)$라면, 다음의 식
\[D(h_1h_2)=\Spec A\setminus Z(h_1h_2)=\Spec A\setminus (Z(h_1)\cup Z(h_2))=(\Spec A\setminus Z(h_1))\cap (\Spec A\setminus Z(h_2))=D(h_1)\cap D(h_2)\]으로부터 $D(f)\subseteq D(h_1)\cap D(h_2)=D(h_1h_2)$임을 안다. 이 식은 단지 [대수적 구조] §분수체, ⁋명제 8을 기하학적으로 설명한 것에 불과하다.
이제 $\Spec A$의 부분집합 $D(f)$ 위에 정의된 대수적인 함수들의 모임을 $S(f)^{-1}A$로 정의해야 함이 직관적이며, 실제로 그렇게 정의할 것이다. 그 전에 우리는 다음 보조정리를 보인다.
보조정리 4 $D(f)\subseteq D(h)$가 성립하는 것은 적당한 $n\geq 1$이 존재하여 $f^n\in (h)$인 것과 동치이다.
증명
$D(f)\subseteq D(h)$인 것은 $Z(h)\subseteq Z(f)$인 것과 동치이고, 이는 §스펙트럼, ⁋보조정리 6의 셋째 결과에 의하여 $\sqrt{(f)}\subseteq \sqrt{(h)}$인 것과 동치이다.
만일 $\sqrt{(f)}\subseteq \sqrt{(h)}$라면, $(f)\subseteq \sqrt{(f)}\subseteq \sqrt{(h)}$로부터 $f\in \sqrt{(h)}$이고, 따라서 적당한 $n\geq 1$이 존재하여 $f^n\in (h)$여야 함을 안다. 거꾸로 적당한 $n\geq 1$이 존재하여 $f^n\in (h)$라면 $f\in \sqrt{(h)}$로부터 $(f)\subseteq \sqrt{(h)}$이고, 따라서
\[\sqrt{(f)}\subseteq\sqrt{\sqrt{(h)}}=\sqrt{(h)}\]이다.
이 보조정리를 활용하면 $S(f)^{-1}A$를 더 깔끔한 방식으로 표현할 수 있다.
보조정리 5 임의의 $f\in A$에 대하여, 다음의 isomorphism
\[S(f)^{-1}A\cong S_f^{-1}A\]이 존재한다. 뿐만 아니라, 만일 $S(g)\subseteq S(f)$라면 다음의 diagram
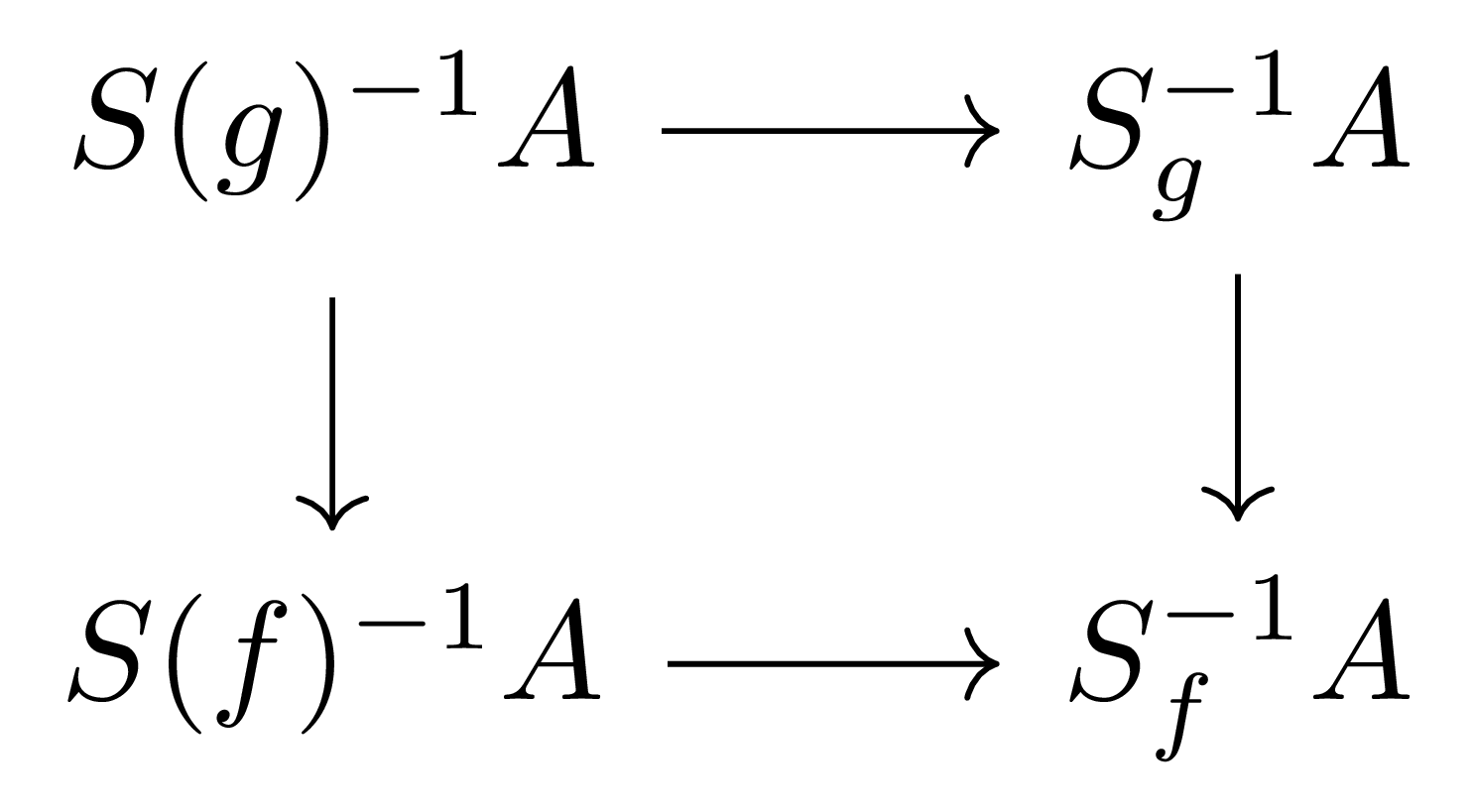
이 commute한다.
증명
우선 canonical morphism들을 $\epsilon(f): A \rightarrow S(f)^{-1}A$, $\epsilon_f:A \rightarrow S_f^{-1}A$으로 표기하기로 하자. 그럼 임의의 $n\geq 1$에 대하여 $D(f)=D(f^n)$이므로, $f^n\in S(f)$가 성립하고 따라서 $S_f$의 $\epsilon(f)$에 의한 image는 모두 $S(f)^{-1}A$의 unit이다. 따라서 [가환대수학] §국소화, ⁋명제 6로부터 다음의 commutative diagram
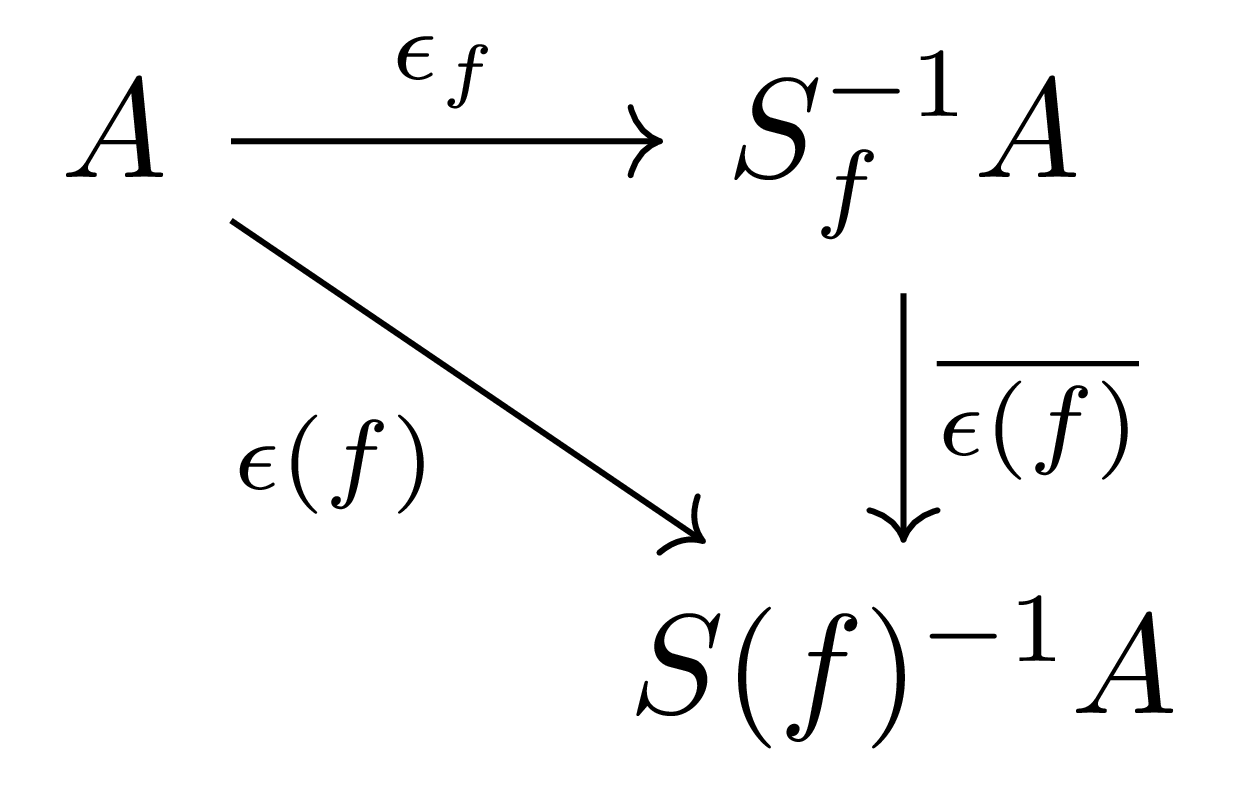
을 얻는다.
이제 다음의 동치관계
\[D(f)\subseteq D(g)\iff f^n\in (g)\text{ for some $n\geq 1$}\iff f^n=ag\text{ for some $n\geq 1$ and $a\in A$}\tag{$\ast$}\]를 관찰하자. 그럼 $D(f)\subseteq D(g)$를 만족하는 임의의 $g$에 대하여, 우리는 $f^n=ag$를 만족하는 적당한 $n\geq 1$과 $a\in A$를 찾을 수 있으므로,
\[\frac{g}{1}\frac{a}{f^n}=1\qquad\text{in $S_f^{-1}A$}\]로부터 $g$는 $S_f^{-1}A$의 unit임을 안다. 따라서 다시 [가환대수학] §국소화, ⁋명제 6로부터 다음의 commutative diagram
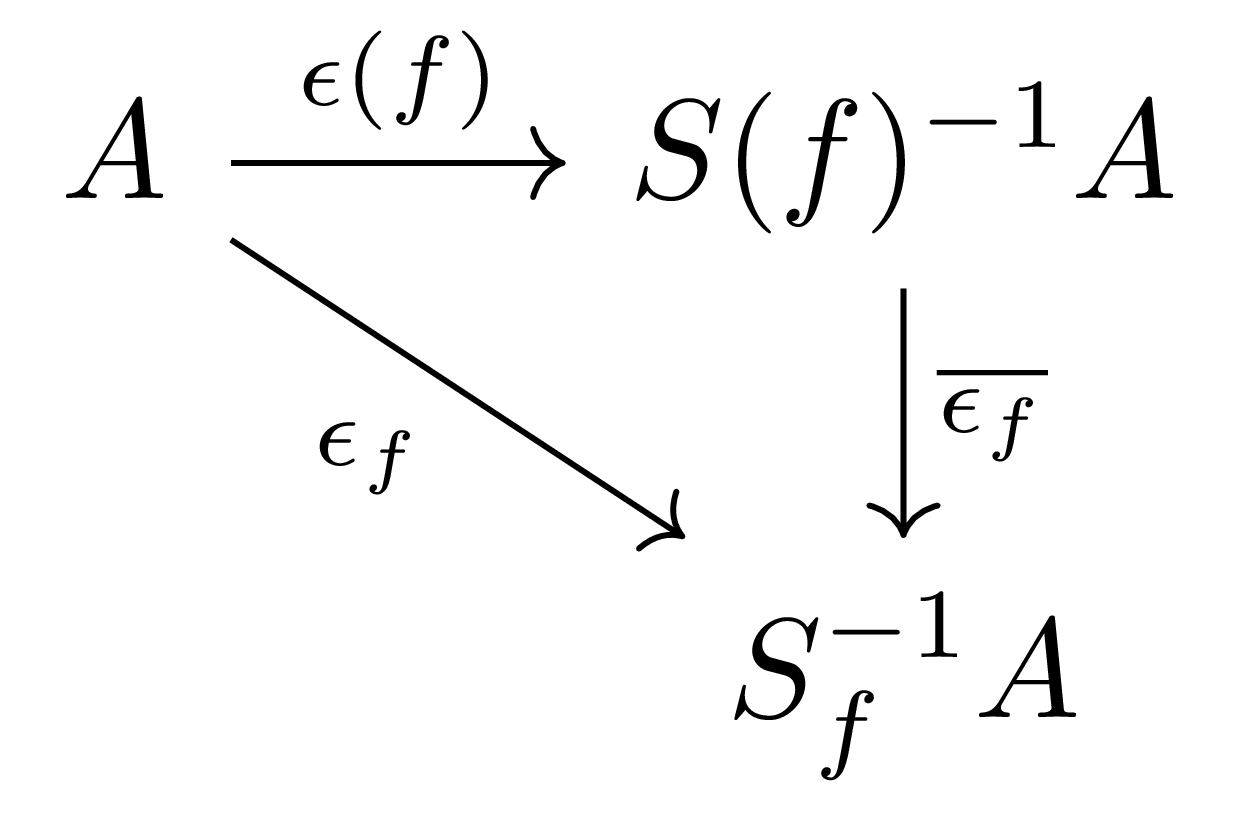
을 얻는다. 이제 $\overline{\epsilon(f)}$와 $\overline{\epsilon_f}$가 서로의 역함수임은 유일성으로부터 자명하다.
이제 $S(g)\subseteq S(f)$라 하자. 그럼 $\widehat{\epsilon(f)}:S(g)^{-1}A \rightarrow S(f)^{-1}A$는 마찬가지로 [가환대수학] §국소화, ⁋명제 6을 통해 다음의 diagram
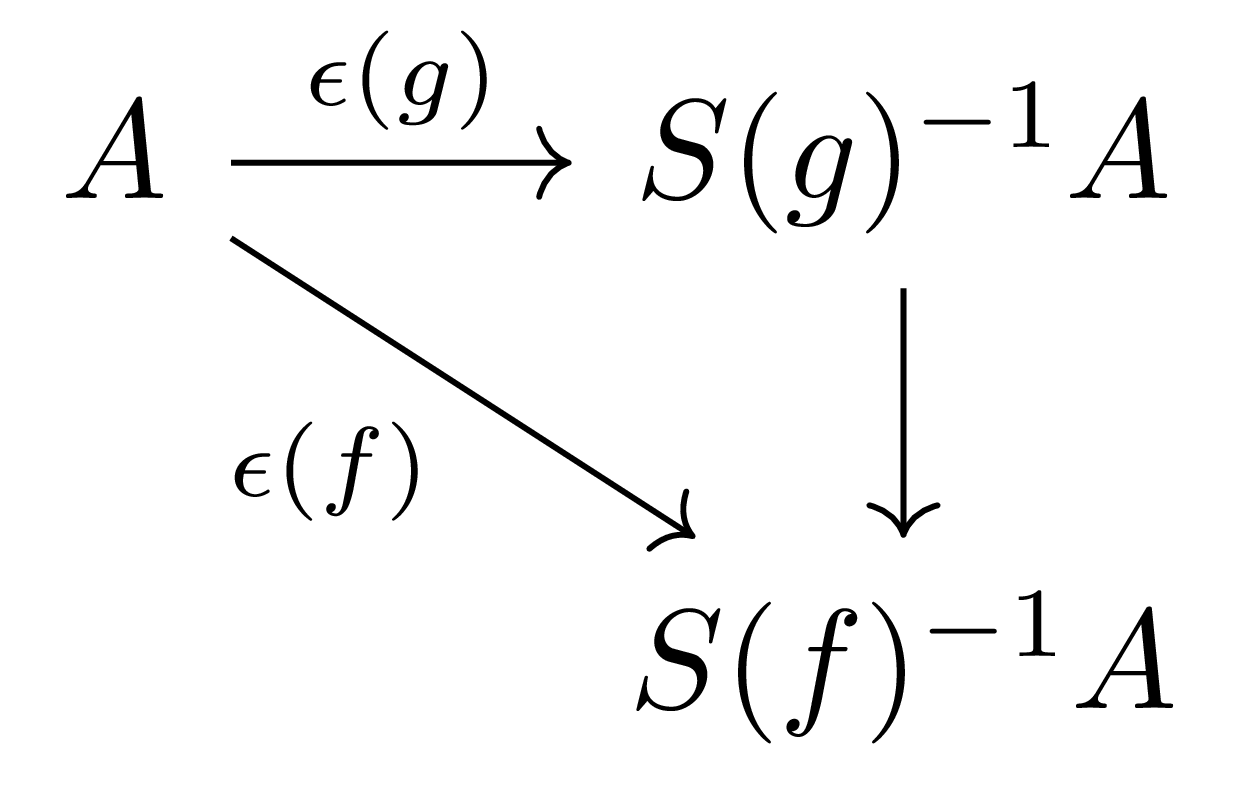
으로 자명하게 정의되는 것이며, 또 $S(g)\subseteq S(f)\iff D(f)\subseteq D(g)$이므로 위의 동치관계 ($\ast$)로부터 $g$는 $S_f^{-1}A$의 unit이며, 따라서 $g^k$들도 모두 마찬가지이다. 이로부터 $\widecheck{\epsilon_f}: S_g^{-1}A \rightarrow S_f^{-1}$를 포함하는 다음의 commutative diagram
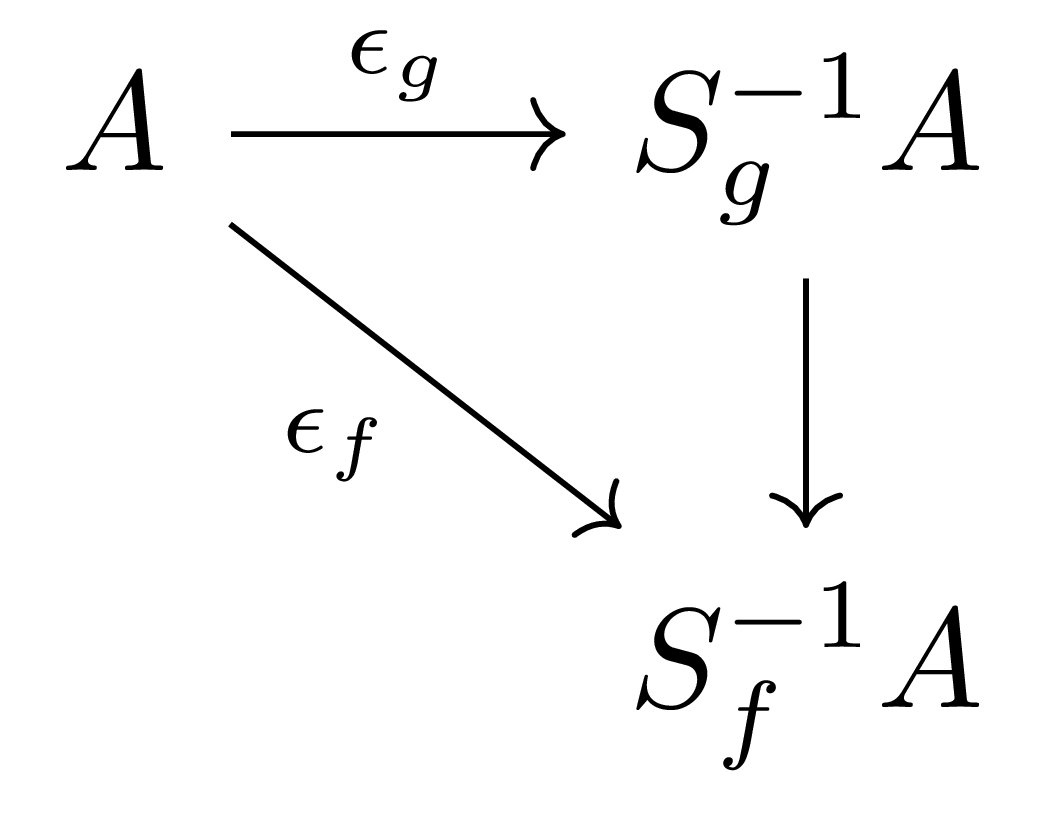
이 존재한다. 그럼 주장의 diagram이 commute한다는 것은 다음 diagram

을 생각하면 자명한데, 즉
\[\epsilon_f=\widecheck{\epsilon_f}\circ\epsilon_g=\widecheck{\epsilon_f}\circ\overline{\epsilon_g}\circ\epsilon(g)\]그리고
\[\epsilon_f=\overline{\epsilon_f}\circ\epsilon(f)=\overline{\epsilon_f}\circ\widehat{\epsilon(f)}\circ\epsilon(g)\]으로부터 $\epsilon_f$는 $S(g)$의 원소들을 $S_f^{-1}A$의 unit으로 보내는 것을 알고, 뿐만 아니라 [가환대수학] §국소화, ⁋명제 6을 통해 $\epsilon_f=\widetilde{\epsilon_f}\circ\epsilon(g)$를 만족하도록 정의되는 $\widetilde{\epsilon_f}$의 유일성으로부터 $\widecheck{\epsilon_f}\circ\overline{\epsilon_g}=\overline{\epsilon_f}\circ\widehat{\epsilon(f)}$임을 얻는다.
따라서, $D(f)$ 위에 정의된 대수적인 함수들은 $S_f^{-1}A$의 원소인 것으로 생각하여도 충분하다. 앞선 글에서 우리는 편의상 $S_f^{-1}A$를 $A_f$로 표기하기로 하였다.
보조정리 6 $\Spec A$의 base $\{D(f)\}_{f\in A}$들에 대하여, 각각의 $f_i\in A$마다
\[\mathscr{F}(D(f_i))=S(f_i)^{-1}A\cong A_{f_i}\]으로 정의하자. 또, $D(f_i)\subseteq D(f_j)$를 만족하는 $f_i,f_j\in A$마다 restriction map
\[\rho_{ji}: S(f_j)^{-1}(A) \rightarrow S(f_i)^{-1}(A)\]을 canonical morphism $A\rightarrow S(f_i)^{-1}(A)$에 [가환대수학] §국소화, ⁋명제 6을 적용하여 얻어지는 함수로 정의하자. 그럼 이들 데이터는 [위상수학] §층, ⁋명제 8의 두 조건을 만족하고, 따라서 $\mathscr{F}$를 확장하는 $\Spec A$의 ($\cRing$-valued) sheaf가 유일하게 결정된다.
증명
$\rho_{ji}$들이 restriction map의 조건([위상수학] §준층, ⁋정의 2)을 만족하는 것은 [가환대수학] §국소화, ⁋명제 6의 universal property로부터 자명하다. 여기에서 $\rho_{ji}: S(f_j)^{-1}(A) \rightarrow S(f_i)^{-1}(A)$는, 보조정리 5에 의하여, 단순히 $S(f_j)^{-1}(A)$의 원소를 다음의 꼴
\[g/h,\qquad\text{where $h\in S(f_j)$}\tag{$\ast$}\]로 나타냈을 때, 다음 식
\[h\in S(f_j)\iff D(f_j)\subseteq D(h)\implies D(f_i)\subseteq D(h)\iff h\in S(f_i)\]로부터 ($\ast$)를 $S(f_i)^{-1}(A)$의 원소로도 볼 수 있으므로 이 과정을 통해 $g/h\in S(f_j)^{-1}(A)$를 $g/h\in S(f_i)^{-1}(A)$로 이해하는 함수이다.
이제 [위상수학] §층, ⁋명제 8의 두 조건을 증명한다. 표기의 편의를 위해 $D(f)=\Spec A_f$이므로, $A$를 $A_f$로 바꾸고 나면 $f=1$인 경우만 생각하면 충분하다. $\Spec A=\bigcup_{i\in I}D(f_i)$를 만족하는 $f_i\in A$들을 고정하자.
우선 첫째 조건을 보이기 위해, 원소 $s\in A$가 모든 $i\in I$에 대해 $S(f_i)^{-1}A$에서 $s=0$를 만족한다 하고, $s$가 $A$의 원소로서도 $0$이 됨을 보이자. 그럼 §스펙트럼, ⁋보조정리 12에 의해 $(f_i)$의 원소들 중 $\Spec A=\bigcup_{i=1}^n D(f_i)$이도록 하는 $f_1,\ldots, f_n$을 택할 수 있고, 가정에 의해 모든 $i=1,\ldots, n$에 대해 다음의 식
\[f_i^{m_i}s=0\]을 만족하는 $m_i$들이 존재한다. 한편 §스펙트럼, ⁋보조정리 11 이후의 계산으로부터 $D(f_i^{m_i})=D(f_i)$가 모든 $i$에 대해 성립하므로,
\[\Spec A=\bigcup_{i=1}^n D(f_i^{m_i})\]이고, 이로부터 $1=\sum_{i=1}^n a_i f_i^{m_i}$이도록 하는 $a_i\in A$들이 존재한다. (참고: §스펙트럼, ⁋보조정리 12의 증명, 혹은 [가환대수학] §정수적 확장, ⁋명제 15의 증명)
따라서
\[s=1s=\left(\sum_{i=1}^n a_i f_i^{m_i}\right)s=\sum_{i=1}^n a_i (f_i^{m_i}s)=0\]이다.
이제 둘째 조건을 보이기 위해, 각각의 $i$마다 $S(f_i)^{-1}A$의 원소 $s_i=a_i/f_i^{m_i}$가 존재하여, 각각의 $i,j$마다
\[\frac{a_i}{f_i^{m_i}}=\frac{a_j}{f_j^{m_j}}\quad\text{ in $D(f_i)\cap D(f_j)=D(f_if_j)$}\]이도록 할 수 있다. 그런데 $D(f_i)=D(f_i^{m_i})$이고 $D(f_j)=D(f_j^{m_j})$이므로
\[D(f_if_j)=D(f_i)\cap D(f_j)=D(f_i^{m_i})\cap D(f_j^{m_j})=D(f_i^{m_i}f_j^{m_j})\]이고, 따라서 적당한 $N_{ij}$가 존재하여
\[(f_i^{m_i}f_j^{m_j})^{N_{ij}}(a_jf_i^{m_j}-a_if_j^{m_i})=0\]이도록 할 수 있다. $N=\max_{i,j}\{N_{ij}\}$라 하여
\[(f_i^{m_i}f_j^{m_j})^N(a_jf_i^{m_j}-a_if_j^{m_i})=0\]즉,
\[a_if_i^{Nm_i}f_j^{Nm_j+m_j}=a_jf_j^{Nm_j}f_i^{Nm_i+m_i}\]를 얻자. 그럼 주어진 가정
\[\Spec A=\bigcup_{i=1}^n D(f_i)=\bigcup_{i=1}^n D(f_i^{Nm_i+m_i})\]로부터 우리는 적당한 $b_i\in A$들이 존재하여
\[1=\sum_{i=1}^n b_ia_if_i^{Nm_i+m_i}\]이도록 할 수 있다. 이제 $s=\sum_{i=1}^n b_ia_i f_i^{Nm_i}$라 하면,
\[sf_j^{Nm_j+m_j}=\sum_{i=1}^n b_ia_i f_i^{Nm_i} f_j^{Nm_j+m_j}=\sum_{i=1}^nb_ia_jf_j^{Nm_j}f_i^{Nm_i+m_i}=a_jf_j^{Nm_j}\]이므로 $f_j^{Nm_j}(sf_j^{m_j}-a_j)=0$이 모든 $j$에 대해 성립하고, 따라서 $D(f_j)$에서
\[\frac{s}{1}=\frac{a_j}{f_j^{m_j}}\]이다. 이로부터 원하는 $s$를 얻는다.
만일 $I$가 무한집합일 경우, $\Spec A=\bigcup_{j\in J} D(f_j)$를 만족하는 $I$의 유한한 부분집합 $J=\{1,\ldots, n\}$을 택하여 위와 같이 반복하여 $s\in \mathscr{F}(\Spec A)$를 얻은 후 이것이 $\alpha\in I\setminus J$인 $D(f_\alpha)$에서도 $s_\alpha=s\vert_{D(f_\alpha)}$를 만족함을 보이면 된다. 이를 보이기 위해 유한집합
\[J\cup\{\alpha\}=\{1,2,\ldots, n,\alpha\}\subseteq I\]에 대해서도 위와 같은 과정을 반복하여 $s’\in \mathscr{F}(\Spec A)$를 얻자. 그럼 $s$와 $s’$는 정의에 의해 $i=1,\ldots, n$마다 $s\vert_{D(f_i)}=s’\vert_{D(f_i)}$를 만족하고 $\Spec A=\bigcup D(f_i)$이므로, 위에서 보인 [위상수학] §층, ⁋명제 8의 첫째 조건에 의해 $s=s’$임을 알고 이로부터
\[s\vert_{D(f_\alpha)}=s'\vert_{D(f_\alpha)}=s_\alpha\]임을 안다. 이것이 모든 $\alpha$에 대해 성립하므로 $s$는 임의의 $D(f_\alpha)$로 제한했을 때도 $s_\alpha$가 된다.
정의 7 보조정리 5에 의해 정의되는 $\Spec A$ 위의 sheaf를 $\mathscr{O}_{\Spec A}$로 쓰고, 이를 structure sheaf라 부른다.
그럼 $(\Spec A,\mathscr{O}_{\Spec A})$는 locally ringed space 이다.
보조정리 8 $(\Spec A,\mathscr{O}_{\Spec A})$와 임의의 점 $\mathfrak{p}\in \Spec A$에 대하여, isomorphism
\[A_\mathfrak{p}\cong \mathscr{O}_{\Spec A, \mathfrak{p}}=\varinjlim_\text{\scriptsize $U\ni\mathfrak{p}$ open} \mathscr{O}_{\Spec A}(U)\]이 존재한다. 뿐만 아니라, $\mathfrak{p}\in D(f)$를 만족하는 임의의 $f\in A$에 대하여, 다음의 diagram
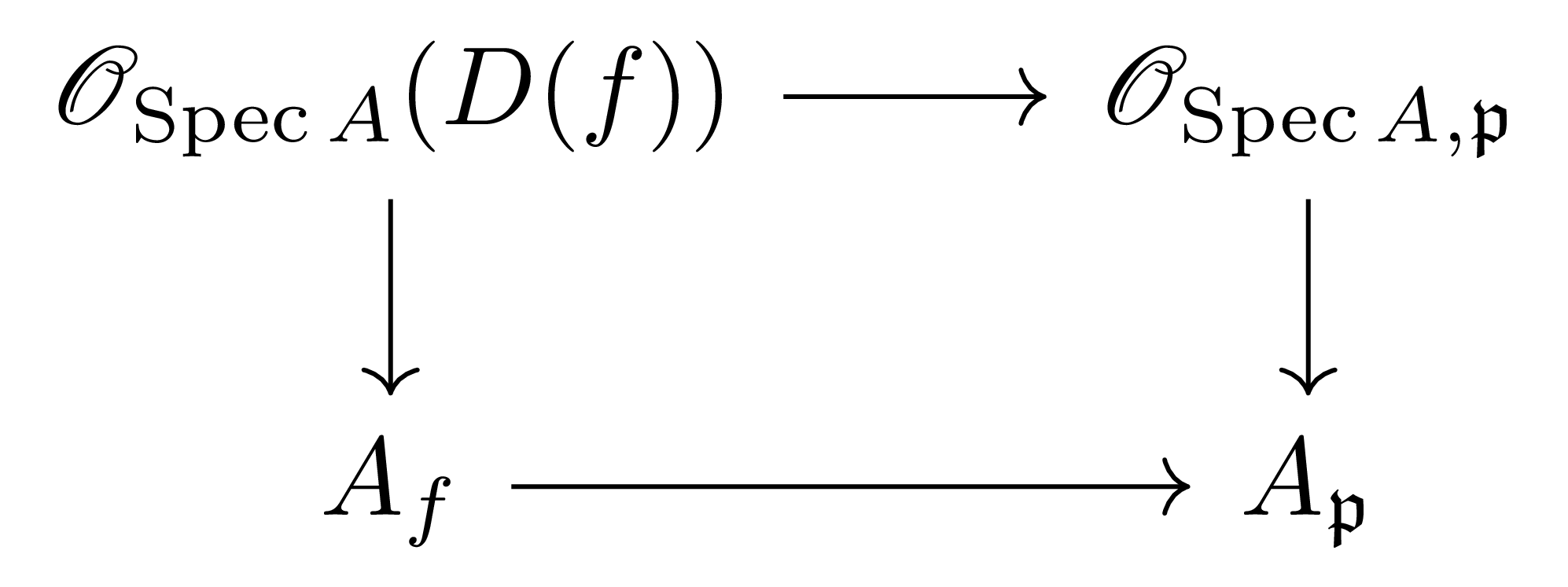
이 commute한다.
증명
§스펙트럼, ⁋보조정리 11에 의하여 $D(f)$들이 $\Spec A$의 base이므로, [위상수학] §위상공간의 기저, ⁋명제 5에 의하여
\[\mathscr{O}_{\Spec A, \mathfrak{p}}=\varinjlim_{D(f)\ni\mathfrak{p}} \mathscr{O}_{\Spec A}(D(f))\]이 성립한다. 한편 $\mathfrak{p}\in D(f)\iff f\not\in \mathfrak{p}$이므로, 우리는 다음의 diagram

을 얻고, 따라서 주어진 isomorphism을 보이는 것은 단순히 다음의 대수적인 isomorphism
\[A_\mathfrak{p}\cong \varinjlim_{\mathfrak{p}\not\ni f} A_f\tag{$\ast\ast$}\]을 보이는 것과 같고, 이는 localization의 universal property ([가환대수학] §국소화, ⁋명제 6)와 direct limit의 universal property를 각각 사용하면 된다. 주장의 diagram은 isomorphism ($\ast\ast$)을 통해 위의 diagram에서 $\varinjlim A_f$를 $A_\mathfrak{p}$로 바꾸어주면 된다.
이제 드디어 $\Spec$의 functoriality를 우리가 원하는 형태로 적을 준비가 되었다.
명제 9 대응 $A\mapsto (\Spec A, \mathscr{O}_{\Spec A})$는 contravariant functor $\Spec: \cRing^\op \rightarrow \LRS$를 정의한다.
증명
우리는 이미 ring homomorphism $\phi: A \rightarrow B$가 연속함수 $\Spec\phi: \Spec B \rightarrow \Spec A$를 유도하는 것을 안다. (§스펙트럼, ⁋명제 8) 따라서
\[(\Spec\phi)^\sharp: \mathscr{O}_{\Spec A} \rightarrow (\Spec\phi)_\ast \mathscr{O}_{\Spec B}\]를 묘사하면 충분하다. 이를 위해서는 principal open set에서의 함수
\[(\Spec\phi)^\sharp(D(f)): \mathscr{O}_{\Spec A}(D(f)) \rightarrow \mathscr{O}_{\Spec B}((\Spec \phi)^{-1}(D(f)))\]를 보면 된다. 한편 §스펙트럼, ⁋명제 8의 증명에서
\[(\Spec\phi)^{-1}(Z(f))=Z(\phi(f))\]이므로
\[(\Spec\phi)^{-1}(D(f))=D(\phi(f))\]임을 안다. 따라서, structure sheaf의 정의에 의하여 $(\Spec\phi)^\sharp(D(f))$를 정의하는 것은
\[A_f \rightarrow B_{\phi(f)}\]를 정의하는 것과 같고, 이는 합성
\[A \overset{\phi}{\longrightarrow}B \overset{\epsilon}{\longrightarrow} B_{\phi(f)}\]에 [가환대수학] §국소화, ⁋명제 6을 적용하여 얻어진다. 물론 이렇게 정의된 $(\Spec\phi)^\sharp$이 교집합 $D(f)\cap D(g)$에서 같은 함수를 정의함을 보여야 하지만, 이는 $D(f)\cap D(g)$임을 이용해서 [가환대수학] §국소화, ⁋명제 6에 유일성 결과를 사용하면 된다.
이상에서 $(\Spec\phi, (\Spec\phi)^\sharp): (\Spec B, \mathscr{O}_{\Spec B}) \rightarrow (\Spec A, \mathscr{O}_{\Spec A})$가 ringed space들 사이의 morphism인 것을 안다. 이제 이것이 locally ringed space들 사이의 morphism임을 보이기 위해서는 임의의 $\mathfrak{q}\in \Spec B$에 대하여
\[(\Spec\phi)^\sharp_\mathfrak{q}:\mathscr{O}_{\Spec A, (\Spec \phi)(\mathfrak{q})} \rightarrow\mathscr{O}_{\Spec B, \mathfrak{q}}\]이 local homomorphism이면 된다. 그런데 $(\Spec \phi)(\mathfrak{q})=\phi^{-1}(\mathfrak{q})$이고, 따라서 보조정리 7에 의하여 $(\Spec\phi)^\sharp_\mathfrak{q}$는 $A_{\phi^{-1}(\mathfrak{q})}$에서 $B_{\mathfrak{q}}$로의 ring homomorphism이며 이는 $A_{\phi^{-1}(\mathfrak{p})}$의 유일한 maximal ideal $\phi^{-1}(\mathfrak{q})A_{\phi^{-1}(\mathfrak{q})}$를 $B_\mathfrak{p}$의 유일한 maximal ideal $\mathfrak{q}B_\mathfrak{q}$로 보낸다.
아핀스킴
정의 10 명제 8의 functor $\Spec:\cRing^\op \rightarrow \LRS$의 essential image를 affine scheme아핀스킴으로 정의한다.
Affine scheme들의 category를 $\AffSch$로 적는다. 그럼 contravariant functor $\Spec:\cRing^\op \rightarrow \AffSch$는 그 정의에 의해 essentially surjective이다. ([범주론] §자연변환, ⁋정리 5) 또, 만일 $(\varphi, \varphi^\sharp): (\Spec B, \mathscr{O}_{\Spec B}) \rightarrow (\Spec A, \mathscr{O}_{\Spec A})$이 어떠한 ring homomorphism $\phi$로부터 유도된 것이라면, 명제 9의 증명에서 $1=f\in A$로 잡으면
\[\varphi^\sharp(D(1))= \bigl(A \overset{\phi}{\longrightarrow} B \overset{\id_B}{\longrightarrow} B_{\phi(1)}=B\bigr)=\phi\]이므로, 이 functor는 반드시 faithful이다. 뿐만 아니라 다음이 성립한다.
명제 11 Functor $\Spec: \cRing^\op \rightarrow \LRS$는 fully faithful이다.
증명
임의의 두 affine scheme $(X, \mathscr{O}_{X})$, $(Y, \mathscr{O}_{Y})$와 이들 사이의 morphism
\[(X, \mathscr{O}_{X}) \rightarrow (Y, \mathscr{O}_{Y})\]이 주어졌다 하면, isomorphism $(\Spec B, \mathscr{O}_{\Spec B})\cong (X, \mathscr{O}_X)$, $(\Spec A, \mathscr{O}_{\Spec A})\cong (Y, \mathscr{O}_Y)$을 통해 이를 두 spectrum들 사이의 (locally ringed space로서의) morphism
\[(\varphi, \varphi^\sharp): (\Spec B, \mathscr{O}_{\Spec B}) \rightarrow (\Spec A, \mathscr{O}_{\Spec A})\]으로 볼 수 있다. 따라서 이 locally ringed space들 사이의 morphism이 적당한 ring homomorphism $\phi$로부터 나오는 것을 증명하면 충분하다. $\Spec$이 faithful이라는 위의 증명에서 힌트를 얻어,
\[\phi=\varphi^\sharp(D(1)):A \rightarrow B\]를 통해 ring homomorphism $\phi:A \rightarrow B$를 정의하면 이제 주장을 완성하기 위해서는 $\Spec\phi=(\varphi,\varphi^\sharp)$임을 보여야 한다. 이는
임의의 $\mathfrak{q}\in \Spec B$에 대하여
\[(\Spec \phi)(\mathfrak{q})=\phi^{-1}(\mathfrak{q})=\varphi(\mathfrak{q})\]임을 보이자. 우선 보조정리 8에서 $f=1$로 두면 우리는 다음의 diagram

을 얻는다. 이 diagram에서 수직방향 함수들은 모두 isomorphism들이고, 다음의 면
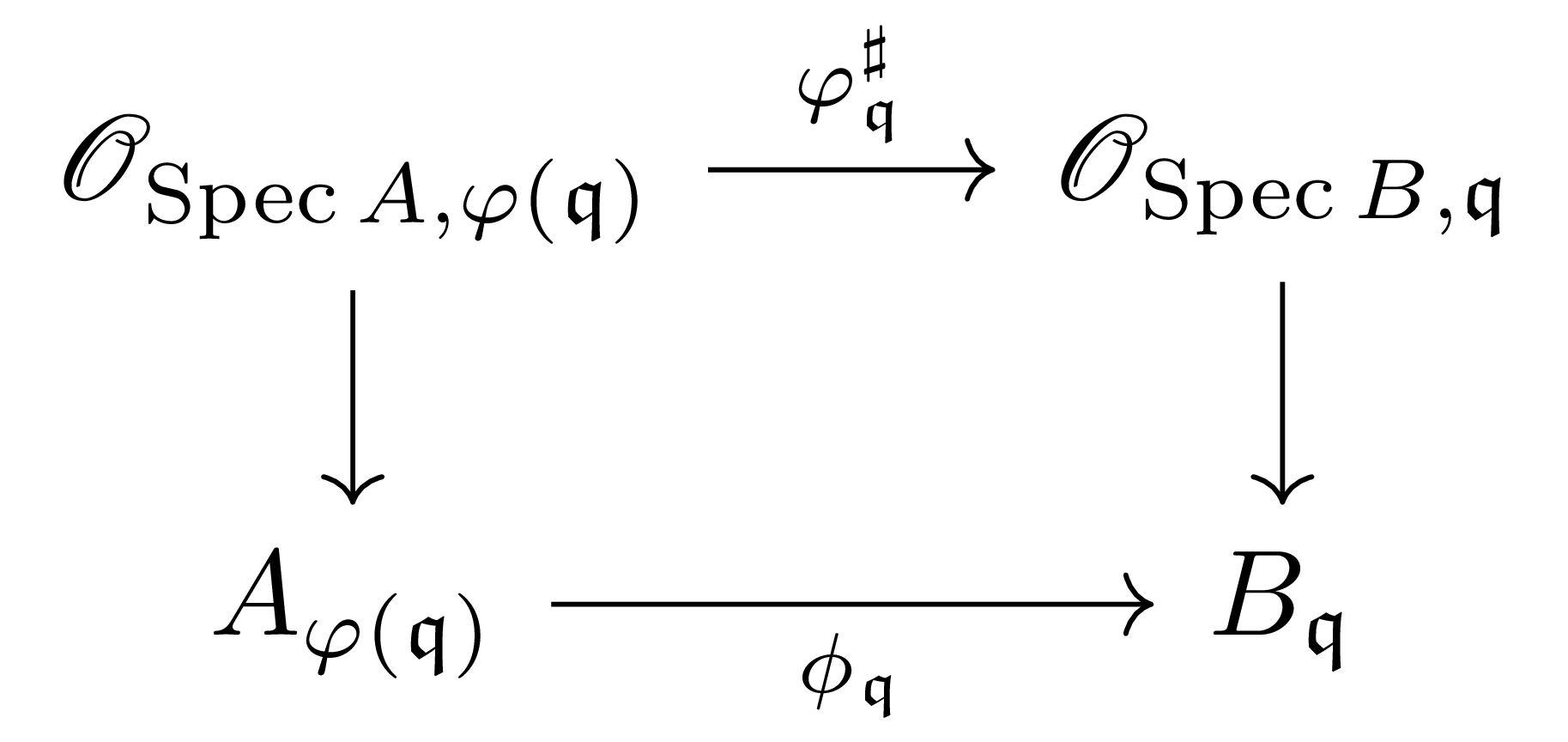
을 제외한 모든 면들은 commuting square임을 알고 있다. 따라서 위의 diagram에서 $A \rightarrow \mathscr{O}_{\Spec B, \mathfrak{q}}$는 어떤 함수를 타고 가도 동일하게 결정되며, 이 함수에 [가환대수학] §국소화, ⁋명제 6를 적용하면 $A_{\varphi(\mathfrak{q})} \rightarrow \mathscr{O}_{\Spec B, \mathfrak{q}}$가 유일하게 결정된다. 이로부터 위의 diagram의
따라서 $\Spec$을 $\cRing$에서 $\AffSch$로의 contravariant functor로 보면 $\Spec$은 두 카테고리 $\cRing^\op$와 $\AffSch$ 사이의 categorical equivalence이다. 뿐만 아니라, 명제 11에 의해 $\AffSch$는 $\LRS$의 full subcategory이다.
[범주론] §자연변환, ⁋정리 5에 의해 $\Spec$이 full인 것만 보이면 충분하다.
한편 임의의 스펙트럼 $(\Spec A, \mathscr{O}_{\Spec A})$에 대하여, 우리는 정의에 의해
\[\mathscr{O}_{\Spec A}(A)=\mathscr{O}_{\Spec A}(D(1))\cong A\]임을 안다. 만일 locally ringed space $(X, \mathscr{O}_X)$가 affine scheme이었다면, 마찬가지 방식으로 $\mathscr{O}_X(X)$를 살펴보아 $(X, \mathscr{O}_X)$가 어떠한 ring의 spectrum과 isomorphic한지 알 수 있다. 즉, affine scheme $(X, \mathscr{O}_X)$에 대하여 $A=\mathscr{O}_X(X)$라 하면 $(X, \mathscr{O}_X)\cong (\Spec A, \mathscr{O}_{\Spec A})$가 성립한다. 더 일반적으로 다음을 정의한다.
정의 12 임의의 locally ringed space $(X, \mathscr{O}_X)$에 대하여, global section functor $\Gamma:\LRS \rightarrow \cRing^\op$를 $X\mapsto \Gamma(X, \mathscr{O}_X)=\mathscr{O}_X(X)$로 정의한다.1
명제 11의 증명에서 주목할 만한 사실은 $(X, \mathscr{O}_X)$가 affine scheme이라는 가정은 필요가 없다는 사실이다. 즉, $(X, \mathscr{O}_X)\cong(\Spec B, \mathscr{O}_{\Spec B})$라는 가정을 버리고 명제 11의 diagram 대신 다음의 diagram

을 사용하여도 비슷한 논증을 해 나갈 수 있으며, 이 때 결론의 $B$는 $\Gamma(X, \mathscr{O}_X)$로 바뀌게 된다. 어차피 $\mathscr{O}_X$는 $X$에 의해 결정되는 데이터이므로, 이를 간략히 $\Gamma(X)$로만 표기하면 이로부터 다음의 정리를 얻는다.
정리 13 임의의 locally ringed space $(X, \mathscr{O}_X)$와 ring $A$에 대하여, 다음의 natural isomorphism
\[\Hom_\LRS(X, \Spec A)\cong \Hom_{\cRing^\op}(\Gamma(X), A)=\Hom_{\cRing}(A, \Gamma(X))\]이 존재한다. 즉, global section functor $\Gamma: \LRS \rightarrow \cRing^\op$는 $\Spec$ functor $\Spec:\cRing^\op \rightarrow \LRS$의 left adjoint이다.
참고문헌
[Har] R. Hartshorne, Algebraic geometry. Graduate texts in mathematics. Springer, 1977.
[Vak] R. Vakil, The rising sea: Foundation of algebraic geometry. Available online.
-
일반적으로 우리는 임의의 $X$ 위의 sheaf $\mathscr{F}$에 대해 $\mathscr{F}(X)$를 $\Gamma(X, \mathscr{F})$로 표기한다. ↩

댓글남기기