자연변환의 정의
우리는 앞서 category들의 category가 존재한다는 것을 보았다. 역시 모든 것이 category라는 믿음을 가지면, 두 category $\mathcal{A},\mathcal{B}$가 주어졌을 때 $\mathcal{A}$에서 $\mathcal{B}$로의 functor들의 category $\Fun(\mathcal{A},\mathcal{B})$가 존재한다는 사실도 어느정도 믿을 수 있다. 우리가 대답해야 할 질문은, 그럼 두 functor $F,G:\mathcal{A}\rightarrow \mathcal{B}$가 주어졌을 때 $F$에서 $G$로의 morphism은 무엇인지이고, 그것이 바로 이번 글에서 정의할 natural transformation이다.
정의 1 두 category $\mathcal{A},\mathcal{B}$가 주어졌다 하고, $\mathcal{A}$에서 $\mathcal{B}$로의 두 functor $F,G$가 주어졌다 하자. 만일 $\obj(\mathcal{A})$를 index set으로 갖는 morphism들의 family
\[\bigl(\alpha_A:F(A)\rightarrow G(A)\bigr)_{A\in\obj(\mathcal{A})}\]이 각각의 $A_1,A_2\in\obj(\mathcal{A})$마다 다음의 diagram
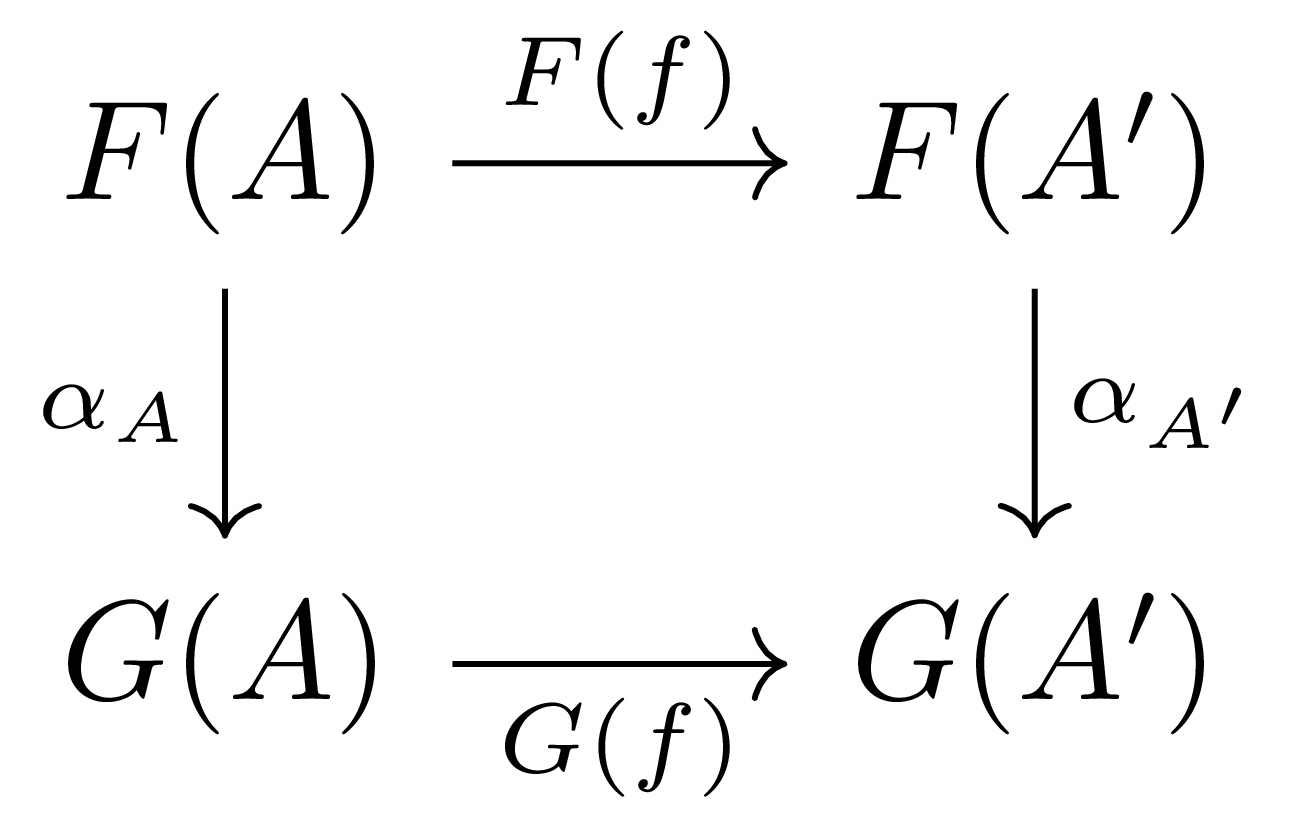
을 commute하도록 한다면, $\alpha=(\alpha_A)_{A\in\obj(\mathcal{A})}$를 natural transformation자연변환이라 부르고 이를 $\alpha:F\Rightarrow G$와 같이 표기한다.
만일 각각의 $\alpha_A$들이 모두 isomorphism이라면 이를 natural isomorphism자연동형변환이라 부르고, 두 functor $F,G$가 naturally equivalent자연변환에 대해 동등하다고 한다. 이를 $F\simeq G$로 표기한다.
이를 바탕으로 category $\mathcal{A}$로부터 $\mathcal{B}$로의 functor category함자 카테고리 $\Fun(\mathcal{A},\mathcal{B})$를 정의할 수 있다. 이는 $\mathcal{A}$에서 $\mathcal{B}$로의 functor들로 이루어진 category로, morphism들은 functor들 사이의 natural transformation이다. 이 category에서의 isomorphism은 natural isomorphism으로 주어진다.
동등한 카테고리들
카테고리 사이에서 자주 사용하는
정의 2 카테고리 $\mathcal{A}$에서 $\mathcal{B}$로의 functor $F$가 equivalence of category동등함자라는 것은 적당한 functor $G:\mathcal{B}\rightarrow \mathcal{A}$가 존재하여 $\id_\mathcal{A}\simeq G\circ F$이고 $\id_\mathcal{B}\simeq F\circ G$인 것이다. 만일 $\mathcal{A}$에서 $\mathcal{B}$로의 equivalence가 존재한다면 이들 두 카테고리가 equivalent동등하다고 하고 $\mathcal{A}\simeq\mathcal{B}$으로 표기한다.
이렇게 정의한 카테고리들 사이의 equivalence라는 개념이 어떤 의미에서 충분히 좋은
정의 3 카테고리 $\mathcal{A}$가 skeletal category뼈대 카테고리라는 것은 임의의 $A\in\obj(\mathcal{A})$에 대하여, $A$와 isomorphic한 $\mathcal{A}$의 object가 자기 자신뿐인 것이다.
$\mathcal{A}$가 small category라 하자. 그럼 집합 $\obj(\mathcal{A})$에서 서로 isomorphic한 대상들을 같은 것으로 본 후, 서로 다른 것들만을 뽑아 $\obj(\mathcal{A})$의 부분집합 $\mathcal{S}$를 만들 수 있다. 임의의 $S_1,S_2\in\mathcal{S}$에 대하여, $\Hom_\mathcal{S}(S_1,S_2)=\Hom_\mathcal{A}(S_1,S_2)$로 두자. 정의로부터 $\mathcal{S}$가 $\mathcal{A}$의 subcategory라면, 자명하게 정의되는 inclusion functor $\mathcal{S}\hookrightarrow\mathcal{A}$가 faithful functor가 된다. 만일 이 functor가 full이기도 하다면 $\mathcal{S}$를 full subcategory충만한 부분카테고리라 부른다.
앞선 논증과 같이 small category $\mathcal{A}$로부터 subcategory $\mathcal{S}$를 만들 경우, $\mathcal{S}$가 $\mathcal{A}$를 설명하기에 충분한 정보를 가지고 있는지가 당연한 의문이 된다. 가령 $\mathcal{A}$에서는 morphism $f:A_1\rightarrow A_2$가 존재하지만, $A_1,A_2$와 isomorphic한 대상들 $A_1’,A_2’$를 택할 경우 morphism $A_1’\rightarrow A_2’$가 존재하지 않는다면 $\mathcal{S}$는 $\mathcal{A}$가 갖고 있는 정보를 잃어버렸다고 할 수 있을 것이다. 하지만 조금만 생각을 해 보면, 이러한 일은 절대로 일어나지 않는다는 것을 알 수 있다. Morphism $f:A_1\rightarrow A_2$가 주어질 때마다, isomorphism들 $A_1’\rightarrow A_1$, $A_2\rightarrow A_2’$와 $f$를 합성하여 $A_1’\rightarrow A_2’$를 만들어낼 수 있기 때문이다.
이러한 관점에서 위에서 만들어낸 카테고리 $\mathcal{S}$는 본질적으로 $\mathcal{A}$의 모든 정보를 담고 있는 것으로 생각할 수 있다. 물론 isomorphic한 대상들 중 어떤 것을 뽑는지에 따라 $\mathcal{S}$ 자체는 달라지겠지만, 다른 선택으로 얻어지는 카테고리도 반드시 $\mathcal{S}$와 isomorphic하다는 것은 쉽게 증명할 수 있다.
정의 4 카테고리 $\mathcal{A}$의 skeleton뼈대은 $\mathcal{A}$의 full subcategory 중 skeletal category인 것을 의미한다. 이를 $\sk(\mathcal{A})$으로 적는다.
다음 정리의 증명은 길고 지루하여 별도로 적어두지 않는다. 그러나 조금만 생각을 해 보면 이 증명에 별도의 아이디어는 필요가 없으며, 꽤나 자명하기까지 하다. 많은 경우에는 equivalence의 정의를 아예 이것으로 받아들이기도 한다.
정리 5 Functor $F:\mathcal{A}\rightarrow\mathcal{B}$가 카테고리들 사이의 equivalence인 것은 $\mathcal{F}$가 fully faithful functor이면서, 다음과 같은 센스에서 essentially surjective본질적 전사 함자인 것과 동치이다.
임의의 $B\in\obj(\mathcal{B})$마다 적당한 $A\in\mathcal{A}$가 존재하여 $F(A)\cong B$가 성립하도록 할 수 있다.
이를 받아들인다면 다음 따름정리 또한 자명하다.
따름정리 6 두 small category $\mathcal{A}$와 $\mathcal{B}$가 equivalent한 것은 이들의 skeletal subcategory $\sk(\mathcal{A})$와 $\sk(\mathcal{B})$가 isomorphic한 것이다.
참고문헌
[Rie] Emily Riehl. Category Theory in Context. Dover Publications, 2016.

댓글남기기