올곱의 정의와 존재성
우리는 §스킴 사이의 사상, ⁋정의 3에서 scheme morpihsm \(X \rightarrow S\)를 \(S\)-scheme이라 부르기로 하였다. 이번 글에서 우리는 category \(\Sch_{/S}\)에서의 product를 정의할 것이다.
정의 1 두 scheme morphism \(\varphi_X:X \rightarrow S\), \(\varphi_Y:Y \rightarrow S\)의 fiber product를 \(X\times_SY\)로 적는다. ([범주론] §극한, ⁋예시 8)
즉, \(X\times_SY\)는 다음의 성질을 만족한다.
다음의 diagram
이 commute한다. 뿐만 아니라, 식 \(\varphi_Y\circ\psi_Y=\varphi_X\circ\psi_X\)를 만족하는 임의의 \(\psi_X:Z \rightarrow X\), \(\psi_Y:Z \rightarrow Y\)가 주어질 때마다 유일한 \(\psi:Z \rightarrow X\times_SY\)가 존재하여 \(\psi_X=\rho_X\circ\psi\)이고 \(\psi_Y=\rho_Y\circ\psi\)이다.
따라서, \(X\times_SY\)에서 \(S\)로의 canonical morphism이 존재하며, 이로부터 우리는 \(X\times_SY\)를 \(S\)-scheme으로 볼 수 있다. 뿐만 아니라, 이 관점에서 \(X\times_SY\)는 \(\Sch_{/S}\)에서의 product이기도 하다는 것이 정의로부터 자명하다.
§스킴 사이의 사상, ⁋예시 4 이후에 우리는 임의의 scheme \(X\)는 항상 유일한 방식으로 \(\mathbb{Z}\)-scheme으로 생각할 수 있다는 것을 보았다. 따라서 정의 1을 만족하는 fiber product \(X\times_SY\)가 항상 존재한다고 가정하면, 우리는 임의의 두 scheme \(X, Y\)에 대하여 \(X\times_{\Spec \mathbb{Z}}Y\)가 \(X\)와 \(Y\)의 product를 주는 것을 안다.
정의 1은 fiber product \(X\times_SY\)의 존재성에 대해서는 어떠한 것도 보장해주지 않으므로, 이것이 진짜 정의가 되기 위해서는 \(X\times_SY\)의 존재성을 별도로 증명해주어야 한다. (정리 6) 그러나 특별히 \(\AffSch\)에서 fiber product의 존재성은 거의 자명하며, 이것이 우리의 증명의 시작이 될 것이다.
보조정리 2 Affine scheme들 사이의 morphism \(\Spec A \rightarrow \Spec C\), \(\Spec B \rightarrow\Spec C\)가 주어졌다 하자. 그럼
\[\Spec A\times_{\Spec C}\Spec B\cong\Spec (A\otimes_C B)\]가 성립한다.
증명
\(\AffSch\cong\cRing^\op\)를 통해 \(\Spec A \rightarrow \Spec C\), \(\Spec B \rightarrow \Spec C\)를 \(C \rightarrow A\), \(C \rightarrow B\)로 바꿔놓고 ##ref##의 universal property와 fiber product의 universal property를 비교하면 된다.
이제 일반적인 scheme에 대해 fiber product가 존재한다는 사실은 보조정리 2에서 살펴본 affine scheme에서의 결과를 바탕으로, 이들을 잘 붙일 수 있다는 것을 보이면 된다.
우선, \(Z\)의 open subscheme \(U\)가 주어졌을 때, 이를 inclusion morphism을 이용하여 \(\iota:U \rightarrow Z\)와 같은 꼴로 쓰면 다음 보조정리는 거의 말장난이다.
보조정리 3 Scheme morphism \(\varphi: Y \rightarrow Z\)와 \(Z\)의 open subscheme \(\iota: U \rightarrow Z\)가 주어졌다 하자. 그럼 다음의 diagram
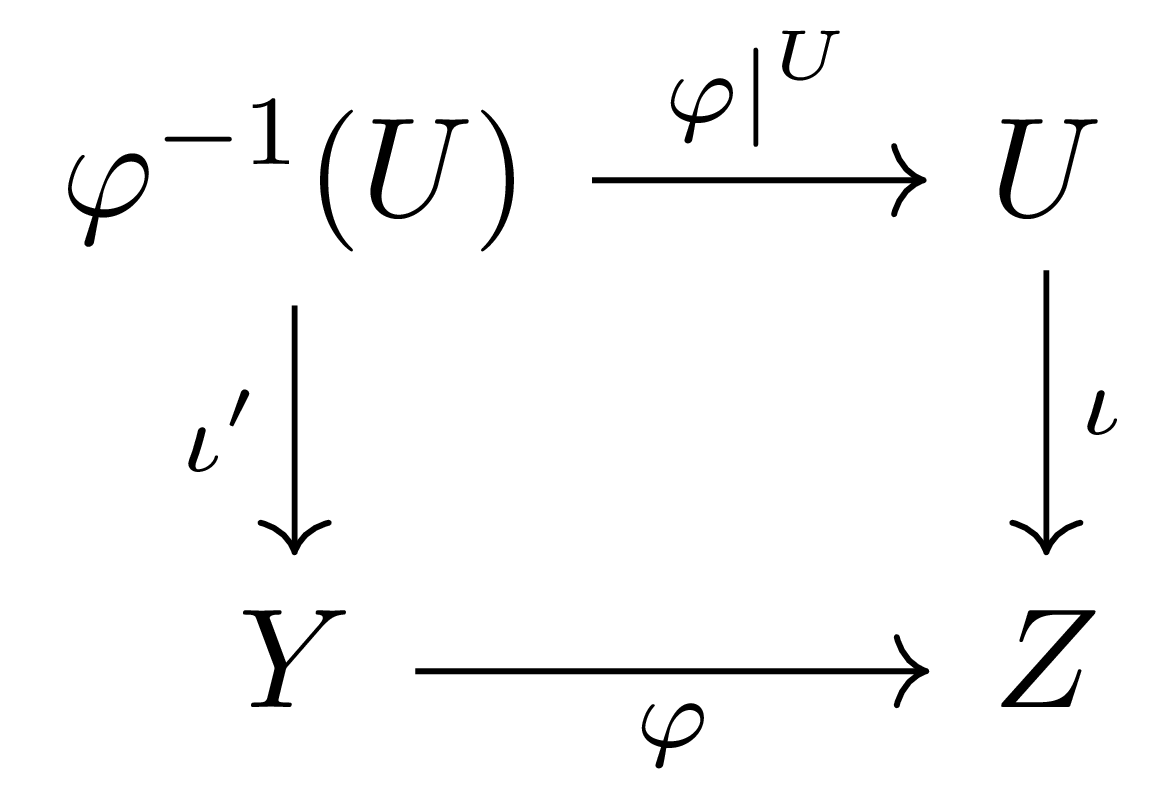
은 fiber diagram이다.
증명
\(\varphi^{-1}(U)\)가 fiber product의 universal property를 만족한다.
이제 이를 약간 활용하면 다음의 보조정리를 보일 수 있다.
보조정리 4 Affine scheme들 \(X, Y, Z\)가 주어졌다 하고, \(Y\)의 open subscheme \(Y'\hookrightarrow Y\)가 주어졌다 하자. 그럼 \(X\rightarrow Z\)와 \(Y'\hookrightarrow Y \rightarrow Z\)의 fiber product \(X\times_ZY'\)가 존재한다.
증명
우선 보조정리 2로부터 다음의 fiber diagram
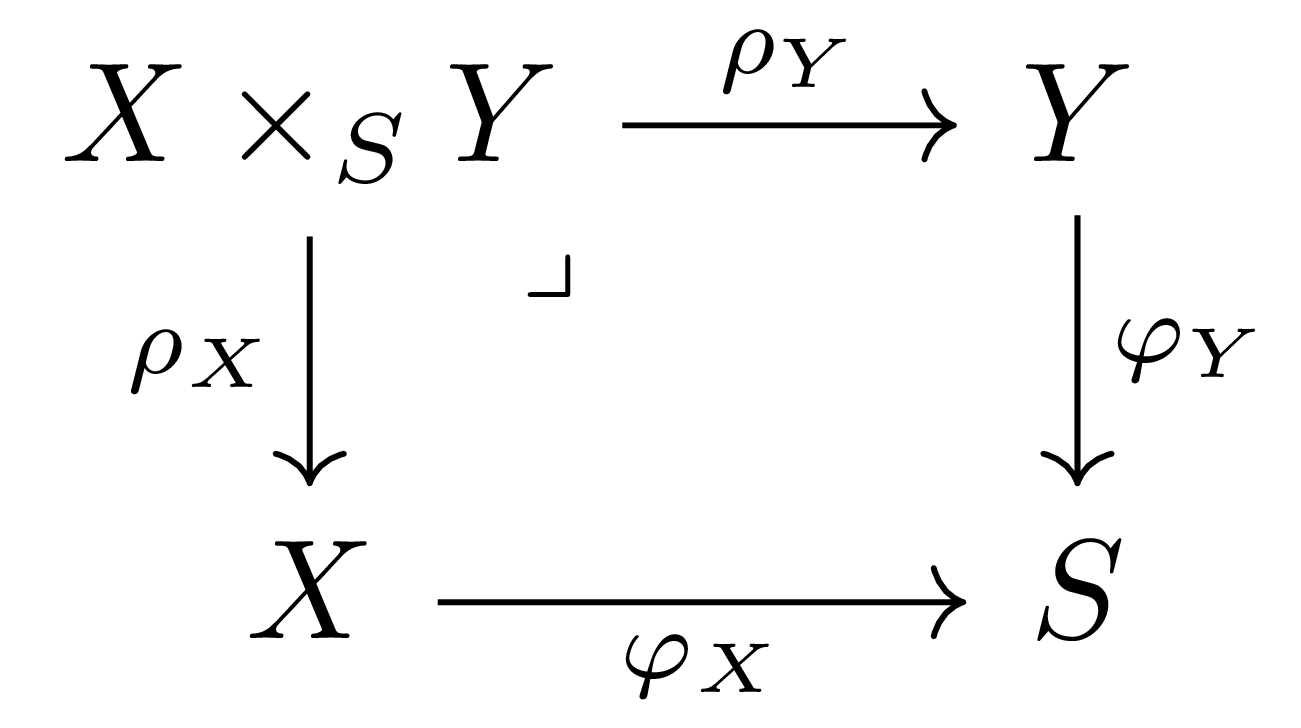
이 존재하는 것을 안다. 이제 다음의 데이터
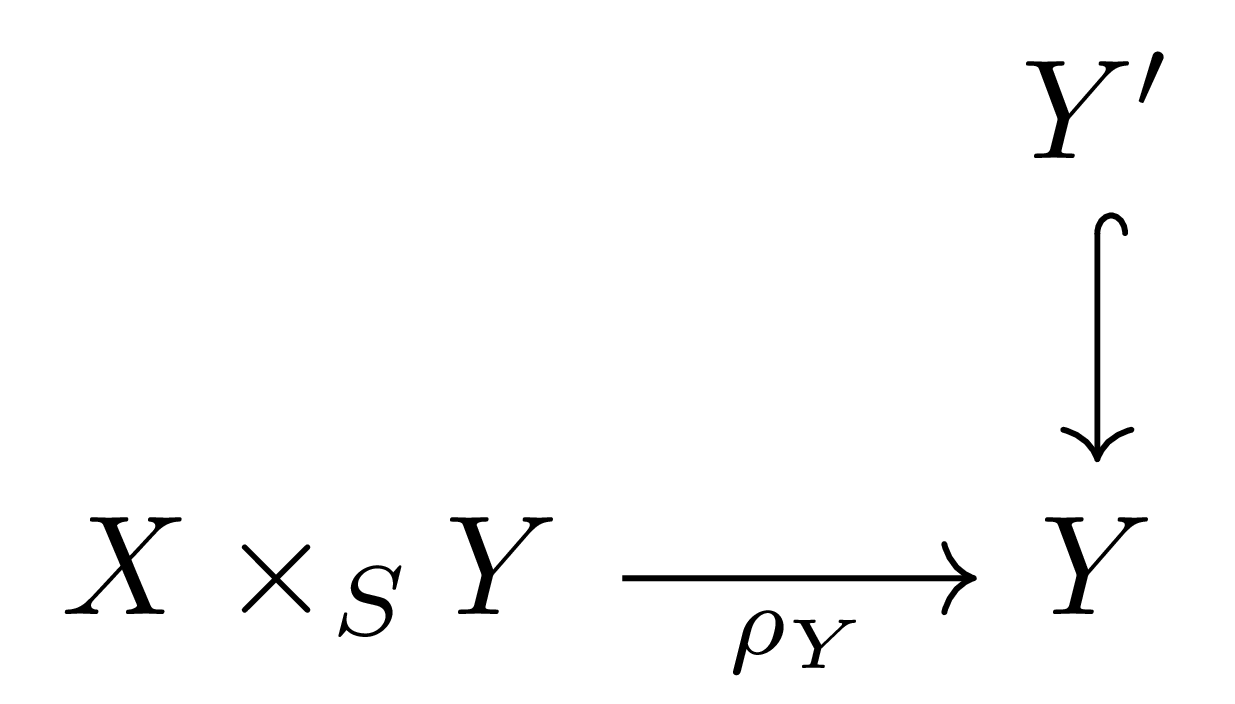
를 생각하면, 우리는 보조정리 3으로부터 \(X\times_SY\)의 open subscheme \(\rho_Y^{-1}(Y')\)가 fiber product가 되는 것을 확인할 수 있다. 이제 일반적으로 다음의 diagram
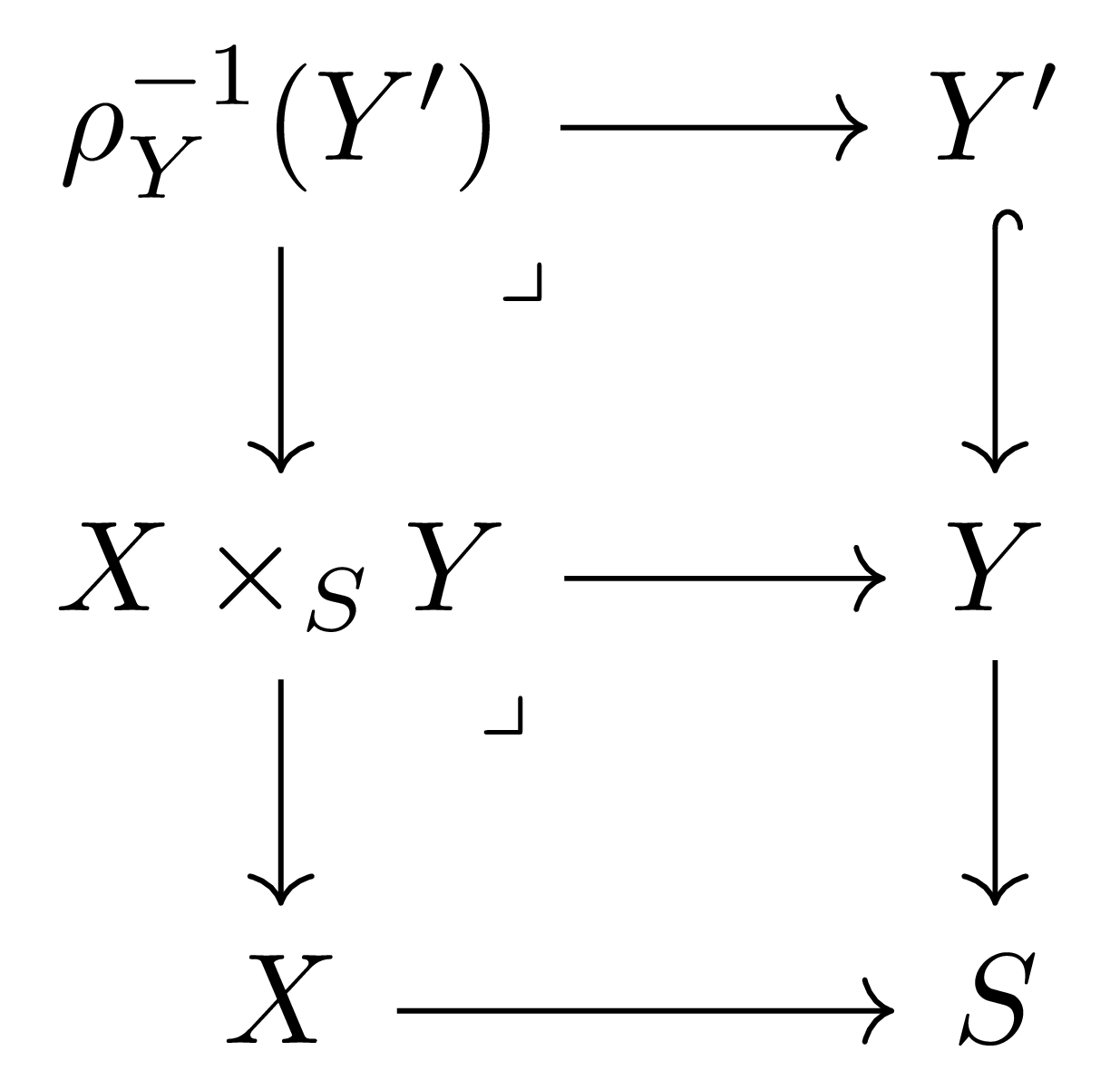
에서 작은 두 사각형이 fiber diagram이라면 외곽의 큰 사각형도 fiber diagram이므로 원하는 결과를 얻는다.
이제 이를 이용하면 affine scheme과 임의의 scheme의 fiber product가 존재한다는 것을 보일 수 있다.
보조정리 5 Affine scheme들 \(X, Z\) 그리고 임의의 scheme \(Y\)에 대하여, \(X\rightarrow Z\)와 \(Y \rightarrow Z\)의 fiber product \(X\times_ZY\)가 존재한다.
증명
이를 위해 \(Y\)를 affine open subset들 \(Y_i\)들로 덮자. 그럼 우리는 보조정리 2으로부터 \(X\times_ZY_i\)들이 존재함을 안다. 또, \(Y_{ij}=Y_i\cap Y_j\)는 affine scheme \(Y_i\)의 open subscheme이므로 역시 \(X\times_Z Y_{ij}\)가 보조정리 4에 의하여 존재한다.
한편, 보조정리 4의 증명을 보면 \(X\times_ZY_{ij}\)는 각각 \(X\times_ZY_i\)와 \(X\times_ZY_{ij}\)의 open subscheme인 것을 알 수 있다. 이들 데이터가 §스킴, ⁋보조정리 9의 조건들을 만족하는 것을 쉽게 확인할 수 있으므로, 이들을 붙여 scheme \(X\times_ZY\)를 만들 수 있다. 이것이 fiber product의 universal property를 만족하는 것은 scheme morphism \(W \rightarrow Y\)의 공역을 \(Y_i\)들로 제한하여 \(X\times_ZY_i\)들 각각의 universal property를 사용한 후, §스킴 사이의 사상, ⁋명제 1과 같이 scheme morphism을 붙여서 만들면 확인할 수 있다.
이 보조정리에서 \(X\)가 affine scheme이라는 가정은 오직 \(X\times_ZY_i\)가 존재한다는 것을 보이기 위해서만 사용되었다. 따라서, 임의의 두 scheme \(X,Y\)와 affine scheme \(Z\), 그리고 scheme morphism \(X \rightarrow Z\)와 \(Y \rightarrow Z\)가 주어졌다 하면 우리는 \(Y\)의 affine open cover \(\{Y_i\}\)를 택한 후, \(X\times_ZY_i\)가 보조정리 5에 의해 존재하는 것을 알고 따라서 이들을 붙여서 \(X\times_ZY\)를 만들 수 있다. 즉 다음이 성립한다.
보조정리 6 Affine scheme \(Z\), 임의의 scheme \(X,Y\)와 scheme morphism \(X \rightarrow Z\), \(Y \rightarrow Z\)에 대하여, fiber product \(X\times_ZY\)가 존재한다.
이제 마지막으로 \(Z\)를 임의의 scheme으로 확장해야 한다. 우선 다음이 성립한다.
보조정리 7 임의의 scheme \(X,Y,Z\)가 주어졌다 하고, scheme morphism \(\varphi_X:X \rightarrow Z\), \(\varphi_Y:Y \rightarrow Z\) 그리고 aßffine scheme \(Z'\)로의 morphism \(\iota: Z \rightarrow Z'\)가 주어졌다 하자. 그럼 \(\iota\circ\varphi_X\)와 \(\iota\circ\varphi_Y\)의 fiber product \(X\times_{Z'}Y\)는 \(X\times_ZY\)의 universal property를 만족하고, 따라서 \(X\times_ZY\)가 존재한다.
이제 위의 보조정리를 이용하여 우리는 임의의 \(X,Y,Z\)와 scheme morphism \(\varphi_X:X \rightarrow Z\), \(\varphi_Y: Y \rightarrow Z\)에 대하여 \(Z\)를 affine open cover \(\{Z_i\}\)들로 덮으면 \(\varphi_X\vert^{Z_i}:\varphi_X^{-1}(Z_i) \rightarrow Z_i\)와 \(\varphi_Y\vert^{Z_i}:\varphi_Y^{-1}(Z_i) \rightarrow Z_i\)에 대해서는 fiber product \(X_i\times_{Z_i}Y_i\)가 존재하는 것을 안다. 이제 교집합 \(Z_{ij}=Z_i\cap Z_j\)은 \(Z_i\)의 열린집합이므로 보조정리 7에 의하여 \(\varphi_X\vert^{Z_{ij}}\)와 \(\varphi_Y\vert^{Z_{ij}}\)의 fiber product들도 존재하며 이는 \(X_i\times_{Z_i}Y_i\)와 \(X_j\times_{Z_j}Y_j\)의 open subscheme이다. 따라서 보조정리 5의 증명과 마찬가지로, 이들 데이터가 §스킴, ⁋보조정리 9의 조건을 만족한다는 것을 보이면 다음 정리를 얻는다.
정리 8 임의의 scheme \(X,Y,Z\)와 scheme morphism \(X \rightarrow Z\), \(Y \rightarrow Z\)에 대하여, fiber product \(X\times_ZY\)가 존재한다.
Fiber product의 해석
Scheme morphism을 해석하는 방법이 여러가지가 존재하듯, fiber product도 이해하는 방법이 여러가지가 있다.
앞서 우리는 scheme morphism \(X \rightarrow S\)를 \(S\)로 parametrize된 family로 생각하기로 하였으며 (§스킴 사이의 사상, ⁋예시 10) 이 관점에서 \(S\)는 family \(X\)의 base로 생각할 수 있다. 이제 임의의 \(S\)-family \(X \rightarrow S\)가 주어졌다 하고, scheme morphism \(S' \rightarrow S\)가 주어졌다 하면 fiber product를 통해 우리는 새로운 \(S'\)-family \(X\times_SS' \rightarrow S'\)를 얻는다. 이러한 관점에서서 우리는 종종 fiber product를 base change라 부르기도 한다.
예시 9 Affine scheme으로 우리의 관심범위를 좁혀보면, \(\Spec B\)가 \(C\)-scheme이라는 것은 scheme morphism \(\Spec B \rightarrow \Spec C\)가 주어졌다는 것이고 이는 다시 ring homomorphism \(C \rightarrow B\)가 주어진 것과 같고 이는 다시 \(B\)가 \(C\)-algebra라는 것과 같은 말이다.
이제 여기에 더해 scheme morphism \(\Spec A \rightarrow \Spec C\)가 주어졌다 하고 위의 base change가 어떠한 것을 주는지를 살펴보면, 보조정리 2에 의해 우리는 이렇게 얻어지는 것이
\[\Spec A\times_{\Spec C}\Spec B=\Spec(A\otimes_CB) \rightarrow \Spec A\]즉 ring homomorphism \(A \rightarrow A\otimes_CB\)임을 안다. 즉, base change는 (affine scheme의 경우에는) 별다른 것이 아니라 [대수적 구조] §스칼라의 변환, ⁋정의 3에 불과하다.
특별히 \(B\)-algebra \(B[\x_1,\ldots,\x_n]\)와 임의의 ring homomorphism \(B \rightarrow A\)에 대하여, 다음 식
\[A\otimes_BB[\x_1,\ldots,\x_n]\cong A[\x_1,\ldots, \x_n]\]이 성립하는 것으로부터 다음의 diagram
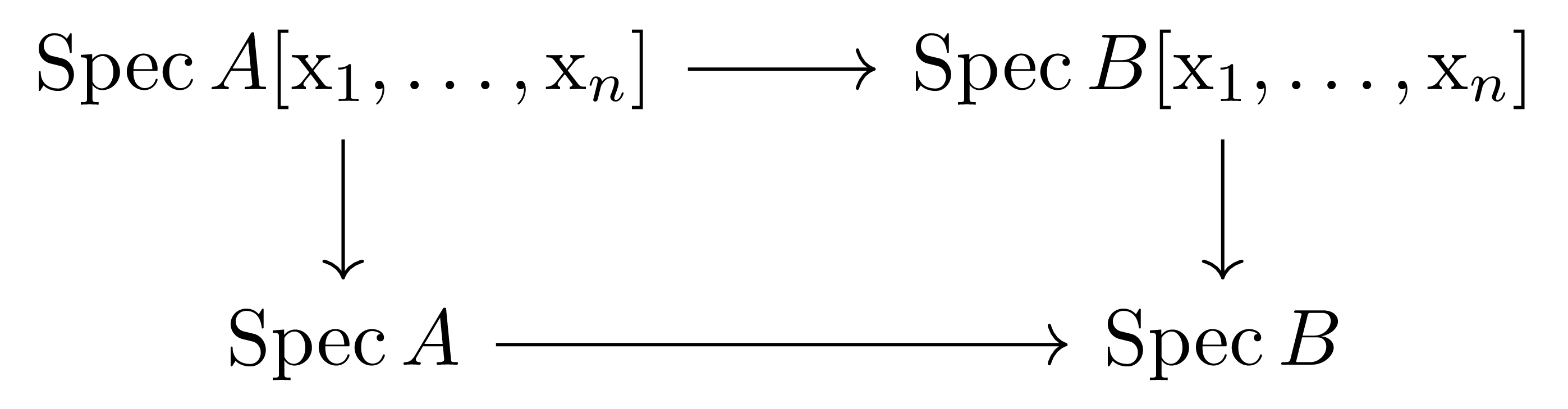
이 fiber diagram인 것을 안다.
이 관점은 중요한 것이지만, 지금 당장은 여기에 있는 기하학적인 직관이 잘 보이지 않는다. 이를 위해 특별히 \(S' \rightarrow S\)가 embedding인 경우를 생각하자.
우선 임의로 주어진 \(S\)-family \(X \rightarrow S\)와 open embedding \(S' \rightarrow S\)가 open embedding에 대하여, 보조정리 3은 \(S'\)-family \(X\times_SS' \rightarrow S'\)가 단순히 \(X \rightarrow S\)의 base를 \(S'\)로 제한하여 얻어진 것임을 보여준다. 여기에 더하여 \(X \rightarrow S\) 또한 open embedding이라 가정하면, 우리는 \(X\times_SS'\)가 (\(S\) 안에서의) \(X\)와 \(S'\)의 교집합임을 안다.
위의 논증은 closed embedding인 경우에도 성립한다. 이를 위해서는 보조정리 3에 해당하는 다음 보조정리를 보여야 한다.
보조정리 10 Ring homomorphism \(\phi: B \rightarrow A\)와 \(B\)의 임의의 ideal \(\mathfrak{b}\)에 대하여, isomorphism
\[A/\phi(\mathfrak{b})A\cong A \otimes_B(B/\mathfrak{b})\]이 존재한다.
증명
Ideal \(\mathfrak{b}\)로부터 얻어지는 다음의 exact sequence
\[\mathfrak{b} \rightarrow B \rightarrow B/\mathfrak{b} \rightarrow 0\]에 \(\otimes_BA\)를 취하면 다음의 exact sequence
\[A\otimes_B \mathfrak{b} \rightarrow A\otimes_BB \rightarrow A\otimes_B (B/\mathfrak{b}) \rightarrow 0\]을 얻고, 이 때 \(A\otimes_B \mathfrak{b}\)의 \(A\otimes_BB\cong A\)에서의 image가 \(\phi(\mathfrak{b})A\)이므로 원하는 결과를 얻는다.
이제 임의의 closed embedding은 국소적으로는 항상 \(B \rightarrow B/\mathfrak{b}\)로부터 오는 것이므로 위의 논의를 closed embedding에 대해서도 동일하게 적용할 수 있다. 특히 두 closed embedding의 교집합이 잘 정의된다.
예시 11 \(Z=\Spec\mathbb{K}[\x,\y]\)의 두 closed subscheme
\[X=\Spec \mathbb{K}[\x,\y]/(\y)=\Spec \mathbb{K}[\x],\qquad Y=\Spec \mathbb{K}[\x,\y]/(\x)=\Spec \mathbb{K}[\y]\]을 생각하자. 그럼 \(X\)와 \(Y\)는 각각 \(Z=\mathbb{A}^2_\mathbb{K}\)의 \(\x\)축과 \(\y\)축에 해당하며, 그 closed embedding은 projection들
\[\mathbb{K}[\x,\y] \rightarrow \mathbb{K}[\x],\qquad \mathbb{K}[\x,\y] \rightarrow \mathbb{K}[\y]\]로 주어진다. 이제 \(X\times_ZY\)는, 보조정리 2에 의하여,
\[\Spec\left(\frac{\mathbb{K}[\x,\y]}{(\x)}\otimes_{\mathbb{K}[\x,\y]} \frac{\mathbb{K}[\x,\y]}{(\y)}\right)\cong \Spec \mathbb{K}[\x,\y]/(\x,\y)\cong\Spec \mathbb{K}\]로 주어지는 것을 확인할 수 있으며 이는 정확히 \(\x\)축과 \(\y\)축의 교점인 원점에 해당한다.
이번에는 위의 계산에서 \(Y\)를 다음의 closed subscheme
\[Y=\Spec \mathbb{K}[\x,\y]/(\y-\x^2)\]으로 바꿔보자. \(\y=\x^2\)과 \(\x\)축의 교점은 마찬가지로 원점이지만, 이번에는 중근이 존재하므로 scheme 구조는 위와 다르게 주어져야 할 것이다. 실제로 계산을 반복하면 \(X\times_ZY\)는
\[\Spec\left(\frac{\mathbb{K}[\x,\y]}{(\y)}\otimes_{\mathbb{K}[\x,\y]}\frac{\mathbb{K}[\x,\y]}{(\y-\x^2)}\right)\cong\Spec \mathbb{K}[\x,\y]/(\y,\y-\x^2)\cong\Spec \mathbb{K}[\x]/(\x^2)\]이 된다.
이 관점에서 우리는 scheme morphism \(\varphi:X \rightarrow Y\)의 \(y_0\in Y\)에서의 fiber \(\varphi^{-1}(y_0)\)을 어떻게 정의해야 하는지도 알 수 있다. \(y_0\)가 closed point이든 아니든, 이를 \(\iota:\{y_0\}\hookrightarrow Y\)로 본 후, \(\iota\)와 \(\varphi\)의 fiber product를 취하면 된다. 이를 위해서는 \(\iota\)를 scheme morphism으로서 기술해야 한다.
이를 위해 \(y\)에서의 residue field \(\kappa(y)\)를 생각하자. 그럼 \(\Spec\kappa(y)\)는 항상 한점집합이다. 뿐만 아니라, \(y\)를 포함하는 \(Y\)의 affine open subset \(V=\Spec B\)를 생각하고, \(y\)가 prime ideal \(\mathfrak{q}_y\)에 대응된다 하면 canonical morphism
\[B \rightarrow B_{\mathfrak{q}_y} \rightarrow B_{\mathfrak{q}_y}/\mathfrak{q}_y B_{\mathfrak{q}_y} =\kappa(\mathfrak{q}_y)=\kappa(y)\]을 통해 \(\Spec\kappa(y)\rightarrow \Spec B\)가 정의되며 \(\Spec \kappa(y)\)의 (유일한) 점 \((0)\)은 위의 morphism을 통해 \(\mathfrak{q}_y\)로 옮겨진다. 따라서 다음을 정의한다.
정의 12 Scheme morphism \(\varphi: X \rightarrow Y\)에 대하여, \(Y\)의 한 점 \(y\in Y\)에서의 fiber올를
\[\varphi^{-1}(y)=X\times_Y\Spec \kappa(y)\]으로 정의한다. 만일 \(Y\)가 irreducible이라면, \(Y\)의 generic point에서의 fiber를 generic fiber라 부른다.
예시 13 Algebraically closed field \(\mathbb{K}\)에 대하여, ring homomorphism \(\mathbb{K}[\x] \rightarrow \mathbb{K}[\y]\)을 식 \(\x \mapsto \y^2\)으로 정의하고, 이로부터 얻어지는 scheme morphism \(\varphi: \Spec \mathbb{K}[\y] \rightarrow \Spec \mathbb{K}[\x]\)를 생각하자. 그럼 \(\Spec\mathbb{K}[\x]\)의 임의의 점 \((\x-a)\)에서의 residue field는
\[\Frac(\mathbb{K}[\x]/(\x-a))=\mathbb{K}[\x]/(\x-a)\]이다. 이제 임의의 \(a\in \mathbb{K}\)에 대하여,
\[\varphi^{-1}((\x-a))=\Spec \mathbb{K}[\y]\otimes_{\Spec \mathbb{K}[\x]}\Spec \mathbb{K}[\x]/(\x-a)\cong \Spec(\mathbb{K}[\y]\otimes_{\mathbb{K}[\x]}\mathbb{K}[\x]/(\x-a))=\Spec \mathbb{K}[\y]/(\y^2-a)\]이며, 따라서 만일 \(a=0\)이라면 \(\varphi^{-1}((\x))\cong\Spec \mathbb{K}[\y]/(\y^2)\)이고, \(a\neq 0\)이라면 \(\mathbb{K}\)가 algebraically closed라는 가정으로부터
\[\Spec \mathbb{K}[\y]/(\y^2-a)\cong \Spec \mathbb{K}[\y]/(\y-\sqrt{a})\coprod \Spec \mathbb{K}[\y]/(\y+\sqrt{a})\]임을 안다. 한편 \(\mathbb{K}[\x]\)의 generic point \((0)\)에 대해서는 \(\kappa((0))=\mathbb{K}(\x)\)이므로
\[\varphi^{-1}((0))=\Spec \mathbb{K}[\y]\otimes_{\Spec \mathbb{K}[\x]}\Spec \mathbb{K}(\x)\cong \Spec\mathbb{K}(\y)\]이 된다.
위의 예시는 이미 §스킴 사상의 성질들, ⁋예시 15에서 살펴보았던 것이다. 해당 예시에서 우리는 finite morphism이 항상 quasi-finite라는 사실을 주장했는데, 이제 이를 증명할 수 있다.
명제 14 Finite morphism \(\varphi: X \rightarrow Y\)는 quasi-finite morphism이다.
증명
Affine인 경우만 보이면 충분하다. 즉, 임의의 finite ring homomorphism \(\phi: B \rightarrow A\)와 \(B\)의 prime ideal \(\mathfrak{q}\)에 대하여 \(A\otimes_B\kappa(\mathfrak{q})\)가 유한히 많은 prime ideal을 갖는다는 것을 보이면 충분하다. 그런데 \(\phi\)가 fintite이므로 \(A\otimes_B\kappa(\mathfrak{q})\)는 finite \(\kappa(\mathfrak{q})\)-algebra이고 따라서 artinian이므로 이로부터 원하는 결과를 얻는다. (##ref##)
위의 예시와 명제들에서 우리는 중요한 관찰을 할 수 있는데, 만일 \(X \rightarrow S\)가 scheme morphism의 어떠한 성질 \(P\)를 만족한다면, 임의의 \(S' \rightarrow S\)로의 base change \(X\times_SS' \rightarrow S'\) 또한 그러하다는 것이다. 이는 우연이 아니며, 실제로 우리가 관심을 가지는 대부분의 성질은 base change에 대해 닫혀있다.
명제 15 만일 scheme morphism \(\varphi:X \rightarrow Z\)가 quasicompact (resp. quasiseparated, affine, finite, integral, locally of finite type, finite type, locally of finite presentation, finite presentation, quasi-finite, surjective) 라면, 임의의 scheme morphism \(Y \rightarrow Z\)를 통해 \(\varphi\)를 base change한 \(X\times_ZY \rightarrow X\) 또한 그러하다.
가령 integral morphism과 finite morphism에 대하여는 [가환대수학] §정수적 확장, ⁋명제 14에서 이를 증명하였으며, 다른 성질에 대해서도 위의 명제를 어렵지 않게 보일 수 있다.

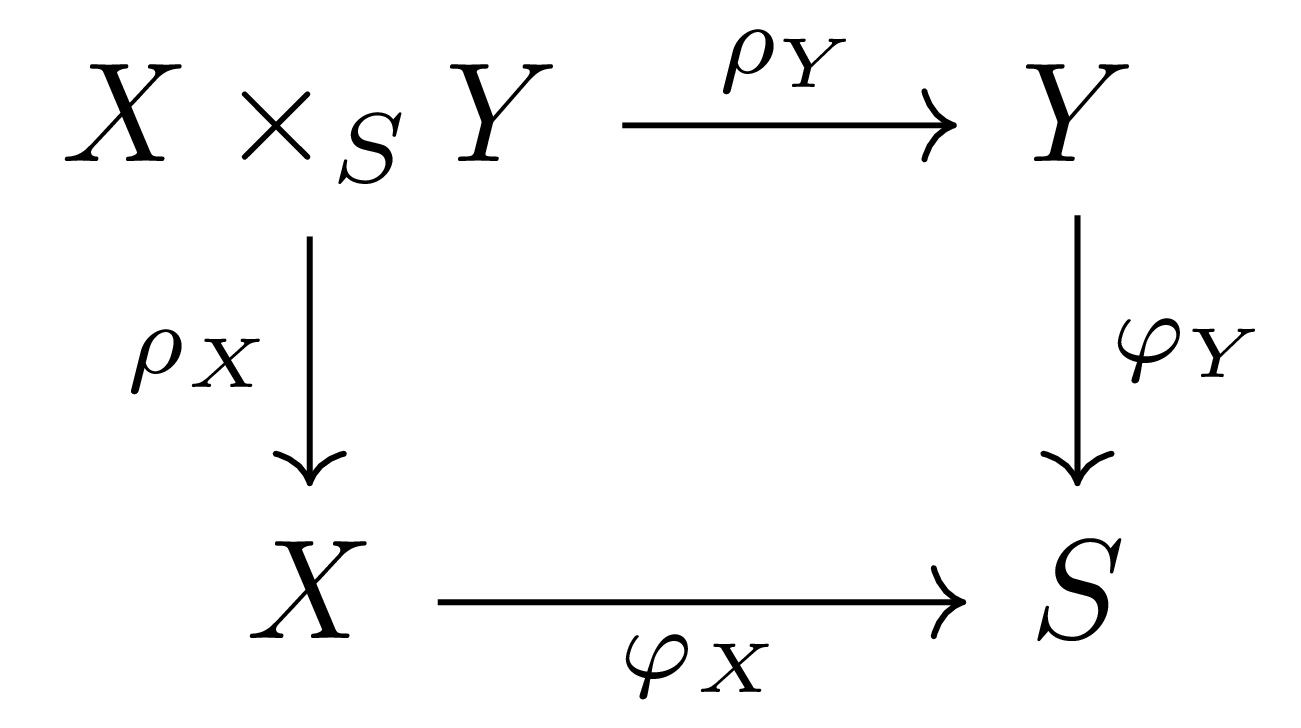

댓글남기기