§스킴, ⁋예시 10에서 우리는 두 개의 affine line \(\mathbb{A}^1=\Spec \mathbb{K}[\x]\)을 적당한 방식으로 붙여 projective space \(\mathbb{P}^1\)을 만들었다. 이번에는 이를 일반화하여 projective scheme을 정의한다.
사영공간
§스킴, ⁋예시 10을 그대로 일반화하면 scheme으로서 \(\mathbb{P}^n\)을 정의하는 것 자체는 어렵지 않다. 하지만 이를 일반화하여 projective scheme을 정의하기 위해서는 \(\mathbb{P}^n\)을 직관적으로 이해하는 것이 도움이 되므로, 이를 조금 더 찬찬히 뜯어보자.
우선 우리는 기존에 위상수학에서 정의하던 projective space를 간단히 살펴본다. 위상공간 \(\mathbb{P}^n\)을 만들기 위해 우리는 위상공간 \(\mathbb{R}^{n+1}\setminus \{0\}\)을 생각했다. 그럼 이 위에 다음의 동치관계
\[(x_0,\ldots, x_n)\sim (y_0,\ldots, y_n)\iff\text{$x_i=\lambda y_i$ for some $\lambda\neq 0$, for all $i$}\]를 정의하면 projective space \(\mathbb{P}^n\)은 quotient space \((\mathbb{R}^{n+1}\setminus \{0\})/{\sim}\)으로 정의되는 위상공간이며, \((x_0,\ldots, x_n)\)을 포함하는 동치류를 표기의 편의를 위해 \([x_0:x_1:\cdots:x_n]\)으로 표기한다.
이 때, canonical projection \(\pi:\mathbb{R}^{n+1}\setminus\{0\}\rightarrow \mathbb{P}^n\)를 생각하자. 그럼 \(\mathbb{P}^n\)의 한 점 \([x_0:x_1:\cdots:x_n]\)의 fiber는 그 정의에 의하여
\[\{(y_0,\ldots, y_n)\mid\text{$x_i=\lambda y_i$ for some $\lambda\neq 0$, for all $i$}\}\]즉 원점과 \((x_0,\ldots, x_n)\)을 지나는 직선 위의 점들 중, 원점을 제외한 점들의 집합으로 주어진다. 이 때문에 \(\mathbb{P}^n\)은 종종 \(\mathbb{R}^{n+1}\)에서의 직선들의 공간으로 생각되기도 한다.
한편, \(\mathbb{R}^{n+1}\)에서, 임의의 평면 \(P\)와, \(P\)와 평행하지 않은 직선은 반드시 한 점에서 만난다. 따라서 평면 \(P_i\)를
\[P_i=\{\x_i=1\}=\{(x_0,\ldots, x_n)\mid x_i=1\}\]로 정의한다면, \(\mathbb{P}^n\)의 점들 중 \(\x_i\)축과 수직인 직선들을 제외한 점들은 모두 \(P_i\)의 점과 일대일로 대응되며, 남아있는 점들은 \(\x_0\x_1\cdots\x_{i-1}\x_{i+1}\cdots\x_n\)-평면, 즉 \(\mathbb{R}^n\)의 직선이므로 다음의 decomposition
\[\mathbb{P}^n=\mathbb{R}^n\coprod \mathbb{P}^{n-1}\]을 얻는다. 이 과정은 \(n=2\)인 경우 다음 그림에 표현되어 있다.
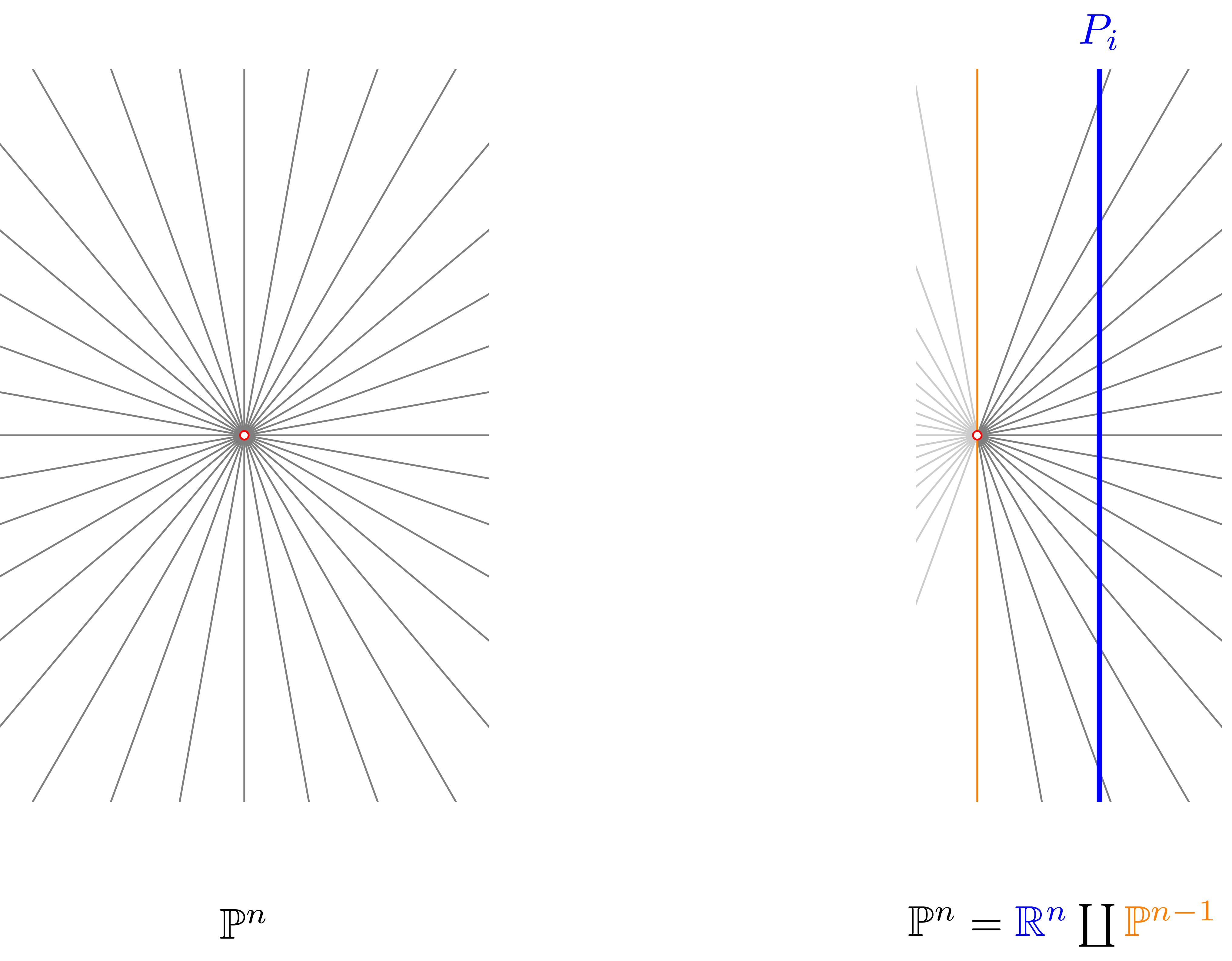
이를 식으로 적으면, \(\mathbb{P}^n\)의 한 점 \([x_0:\cdots:x_n]\)에 대하여, 만일 \(x_i\neq 0\)이라면 \([x_0:\cdots:x_n]\)의 동치류 안에서 \(i\)번째 좌표가 \(1\)이 되는 점을 (유일하게) 찾을 수 있으며, 이 점을 \(P_i\)의 점으로 보아 다음 부분집합
\[U_i=\{[x_0:\cdots:x_n]\in \mathbb{P}^n\mid x_i\neq 0\}\]을 \(P_i\cong \mathbb{R}^n\)과 identify할 수 있다. 한편 \(U_i\)의 여집합에 속한 점들은 정확히 \(x_i=0\)인 점들이므로, 단순히 \(i\)번째 좌표를 생략해서 쓰는 것만으로 이를 \(\mathbb{P}^{n-1}\)의 점으로 이해할 수 있다.
명시적으로 위의 identification \(U_i\cong P_i\)는 다음의 식
\[[x_0:\cdots:x_n]\text{ in $U_i\subseteq \mathbb{P}^n$}\leftrightarrow\left(\frac{x_0}{x_i},\ldots, \frac{x_{i-1}}{x_i},1,\frac{x_{i+1}}{x_i},\ldots, \frac{x_n}{x_i}\right)\text{ in $P_i\subseteq \mathbb{R}^{n+1}$}\]으로 표현된다. 한편, §스킴, ⁋예시 10의 과정은 이 과정을 거꾸로 진행하는 것이다. 즉, \(n+1\)개의 \(n\)차원 평면 \(P_0,\ldots, P_n\)들이 먼저 주어져 있다 하고 이들을 cocycle condition을 만족하는 isomorphism들을 통해서 옮겨주는 것이다. 그럼 cocycle condition이 어떻게 쓰여져야 하는지는 정확히 위의 identification에 의해 \(\mathbb{P}^n\)의 한 점이 서로 다른 \(P_i\)와 \(P_j\)에서 어떻게 쓰여지는지를 살펴보아 얻어진다. 이를 살펴보자. 우선 \(P_i\)와 \(P_j\)의 임의의 점은 다음의 꼴
\[(x_{0/i},\ldots, x_{(i-1)/i}, 1, x_{(i+1)/i}, \ldots, x_{n/i})\in P_i,\qquad (x_{0/j},\ldots, x_{(j-1)/j}, 1, x_{(j+1)/j}, \ldots, x_{n/j})\in P_j\]으로 적을 수 있다. 이제 만일 이들 점이 \(\mathbb{P}^n\)의 어떤 점으로부터 나온 것이라 가정한다면, 그 점은 반드시 \(U_i\cap U_j\)에 속해 있어야 하고, 이 집합에서 \(x_i,x_j\neq 0\)이어야 하므로 \(x_{j/i}, x_{i/j}\neq 0\)이어야 한다. 표기의 편의상 \(j>i\)라 하고, 이 사실을 이용하면
\[[x_{0/i}:\ldots: x_{(i-1)/i}: 1: x_{(i+1)/i}: \ldots: x_{j/i}:\ldots, x_{n/i}]=\left[\frac{x_{0/i}}{x_{j/i}}:\ldots: \frac{x_{(i-1)/i}}{x_{j/i}}: \frac{1}{x_{j/i}}: \frac{x_{(i+1)/i}}{x_{j/i}}: \ldots: 1:\ldots, \frac{x_{n/i}}{x_{j/i}}\right]\]이다. 따라서 우변의 점이
\[[x_{0/j}:\ldots: x_{(j-1)/j}: 1: x_{(j+1)/j}: \ldots: x_{n/j}]\]과 같기 위해서는 다음의 식
\[x_{k/i}/x_{j/i}=x_{k/j}\quad\text{for all $k\neq i,j$},\qquad\text{and}\qquad x_{i/j}=1/x_{j/i}\]이 성립해야 한다. 마찬가지로 \(P_j\)의 점을 \(P_i\)의 점에 맞추면 \(x_{k/j}/x_{i/j}=x_{k/i}\)와 같은 식도 얻어질 것이지만, 이는 \(x_{i/j}=1/x_{j/i}\)에 의해 새로운 식은 아니다.
이제 이 계산을 바탕으로 §스킴, ⁋예시 10를 일반화하자. 우선 \(n+1\)개의 affine \(n\)-space들
\[P_i=\Spec \mathbb{K}[\x_{0/i},\ldots, \x_{n/i}]/(x_{i/i}-1)=\Spec A^i\]를 생각하자. 그럼 \(P_i\)의 open subscheme들 \(P_{ij}=D(\x_{j/i})=(A^i)_{\x_{j/i}}\)과, 다음의 ring homomorphism
\[(A^i)_{\x_{j/i}} \rightarrow (A^j)_{\x_{i/j}};\qquad \x_{k/i}\mapsto \x_{k/j}/\x_{i/j}\quad\text{for all $k\neq i,j$},\qquad\text{and}\qquad \x_{j/i}\mapsto 1/\x_{i/j}\]을 통해 정의되는 isomorphism \(\varphi_{ij}:P_{ij} \rightarrow P_{ji}\)들이 §스킴, ⁋보조정리 9의 cocycle condition을 만족하는 것이 거의 자명하며 따라서 유일한 scheme \(\mathbb{P}^n\)이 정의되고, 이 때 \(\mathbb{P}^n\)의 원소들을 \([x_0:\ldots:x_n]\)의 형태로 쓴다면 \(U_i\)는 정확히 \(x_i\neq 0\)인 조건을 만족하는 집합이다.
사영스킴
현재로서는 위의 설명이 불완전한 부분들이 있다. 가령, \(U_i\)들이 \(\mathbb{P}^n\)의 open subscheme인 것은 §스킴, ⁋보조정리 9의 결과이기는 하지만, 그 정의 자체로도 함수 \(\x_i\)가 \(0\)이 되지 않는 집합이므로 열린집합이 되어야 할 것처럼 보인다. 그러나 문제는 \(\x_i\)가 \(\mathbb{P}^n\) 위의 함수가 아니라는 데에 있다. 심지어 \(n=1\)인 경우만 보아도 우리는 \(\mathscr{O}_{\mathbb{P}^1}(\mathbb{P}^1)\cong \mathbb{K}\)인 것을 확인했다. 이는 위상수학에서의 construction만으로도 확인할 수 있는데, \(\mathbb{R}^{n+1}\setminus \{0\}\)의 한 점 \((x_0,\ldots, x_n)\)을 받아 \(x_i\)를 내놓는 함수 \(\x_i: \mathbb{R}^{n+1}\setminus\{0\} \rightarrow \mathbb{R}\)은 \(\sim\)과 compatible하지 않고 따라서 \(\mathbb{P}^n\) 위의 함수를 정의하지 않는다. 또 다른 예시로 \(\mathbb{R}^2\setminus\{0\}\) 위에서 정의된 함수 \(f: \mathbb{R}^2\setminus\{0\} \rightarrow \mathbb{R}\)가 다음의 식
\[f(x_0,x_1)=x_0^2-x_1\]으로 주어졌다면,
\[f(\lambda x_0,\lambda x_1)=\lambda^2x_0^2-\lambda x_1\neq f(x_0,x_1)\]이 되어 \(f\)가 잘 정의되지 않는다. 그 대신, \(f\)를 homogeneous polynomial로 가져온다면, 함수로서 \(f\)는 잘 정의되지 않더라도 \(f\)의 zero locus \(Z(f)\)는 잘 정의된다. 이는 다음의 식
\[f(\lambda x_0,\ldots, \lambda x_n)=\lambda^{\deg f} f(x_0,\ldots, x_n),\qquad \lambda\neq 0\]이 성립하기 때문이다.
즉, \(\mathbb{P}^n\)을 스펙트럼과 비슷한 방식으로 설명하기 위해서는 \(\mathbb{A}^{n+1}\)을 단순한 ring \(\mathbb{K}[\x_0,\ldots, \x_n]\)의 spectrum으로 볼 것이 아니라, 여기에 degree에 대한 정보를 추가하여 이를 graded ring으로 보고, 임의의 원소들의 zero locus가 아닌 homogeneous한 원소들의 zero locus를 보아야 한다. 그럼 [대수적 구조] §등급환, ⁋명제 6를 생각하면 우리의 관심사 또한 homogeneous ideal들이 되어야 할 것이다.
이번 글의 남은 부분에서 우리는 graded ring에 \(\Proj\)를 취하여 projective scheme을 얻어내는 과정을 따라간다. 이를 위해 몇몇 표기를 고정한다.
Graded ring은 별 말이 없다면 항상 \(\mathbb{N}_{\geq0}\)-graded인 것으로 가정한다. 즉 우리의 관심이 되는 ring은 항상 다음의 꼴
\[A_\bullet=\bigoplus_{i=0}^\infty A_i=A_0\oplus A_1\oplus\cdots\]이다. 이 때, \(A_0\)은 그 자체로 ring이므로, \(A_\bullet\)은 graded \(A_0\)-algebra로 볼 수 있으며, 이러한 이유에서 \(A_0\)을 base ring이라 부른다. 또, \(A_\bullet\)에 정의된 grading 구조를 잊어버리고 이를 평범한 ring으로 볼 일이 있을 때는 이를 간단히 \(A\)로만 적기로 한다.
Graded ring \(A_\bullet\)이 주어졌다 하자. 그럼 다음의 부분집합
\[A_+=\bigoplus_{i=1}^\infty A_i=A_1\oplus A_2\oplus\cdots\]은 \(A_\bullet\)의 homogeneous ideal이 되는 것이 자명하다. 그런데 \(A_\bullet=\mathbb{K}[\x_0,\ldots, \x_n]\)인 경우를 생각하면, \(A_+\)의 모든 원소들에 대해 함숫값이 \(0\)이 되는 점, 즉 모든 다항식에 대해 항등적으로 \(0\)이 되는 점은 오직 원점 뿐이다. 원점은 \(\mathbb{P}^n\)을 만들 때 빠지는 점이므로 ideal \(A_+\)를 포함하는 ideal은 우리의 논의의 대상에서 제외하는 것이 옳을 것이다. 이러한 관점에서 \(A_+\)를 irrelevant ideal이라 부른다.
이제 집합으로서 \(\Proj A_\bullet\)은 다음과 같이 정의된다.
정의 1 Graded ring \(A_\bullet\)에 대하여, \(\Proj A_\bullet\)은 다음의 집합
\[\Proj A_\bullet =\{\mathfrak{p}\in \Spec A\mid\text{$\mathfrak{p}$ is homogeneous and $A_+\not\subset \mathfrak{p}$}\}\]으로 정의된다.
정의에 의해 \(\Proj A_\bullet\)은 \(\Spec A\)의 부분집합이다. 즉, \(\Proj A_\bullet\)의 점들은 모두 \(\Spec A\)의 점들이기도 하다. 이는 \(\Spec A\) 대신 \(\mSpec A\)를 사용했다면 다소 어색한 결과이지만, \(\Spec A\)에는 전통적인 점들 외에도 prime ideal들에 해당하는 점들이 존재한다. 가령 \(A=\mathbb{K}[\x_1,\x_2]\)의 ideal \((\x_1-\x_2)\)를 생각하면, \(\mathbb{K}[\x_1,\x_2]/(\x_1-\x_2)\cong \mathbb{K}[\x_1]\)이므로 이 ideal은 prime ideal이다. 또, 이 ideal은 \(\mathbb{K}[\x_1,\x_2]\)를 graded ring \(A_\bullet\)으로 보았을 때, \(A_+\)를 포함하지 않는 homogeneous prime ideal이므로 \(\Proj A_\bullet\)의 점이기도 하다.
아직까지 \(\Proj A_\bullet\)은 집합일 뿐이다. 여기에 위상구조를 주기 위해서는 함수의 zero locus를 사용해야 하고, 앞서 관찰했듯 우리는 homogeneous polynomial의 zero locus를 사용해야 한다.
정의 2 Graded ring \(A_\bullet\)가 주어졌다 하자. \(A_\bullet\)의 homogeneous ideal \(\mathfrak{a}\)에 대하여
\[Z_+(\mathfrak{a})=\{\mathfrak{p}\in\Proj A_\bullet\mid \mathfrak{a}\subseteq \mathfrak{p}\}\]으로 정의한다.
그럼 [가환대수학] §등급환의 국소화, ⁋보조정리 2의 셋째 결과를 이용하여, §스펙트럼, ⁋보조정리 6, 그리고 §스펙트럼, ⁋명제 5과 비슷한 다음 보조정리를 보일 수 있다.
보조정리 3 Graded ring \(A_\bullet\)에 대하여 다음이 성립한다.
- 임의의 homogeneous ideal \(\mathfrak{a},\mathfrak{b}\)에 대하여, \(Z_+(\mathfrak{a}\mathfrak{b})=Z_+(\mathfrak{a})\cup Z_+(\mathfrak{b})\)이다.
- 임의의 homogeneous ideal들의 family \(\{\mathfrak{a}_i\}\)에 대하여, \(Z_+(\sum \mathfrak{a}_i)=\bigcap Z_+(\mathfrak{a}_i)\)이 성립한다.
- 임의의 homogeneous ideal \(\mathfrak{a}\)에 대하여, \(Z_+(\sqrt{\mathfrak{a}})=Z_+(\mathfrak{a})\)이다.
- 임의의 homogeneous ideal \(\mathfrak{a}\)에 대하여, \(Z_+(\mathfrak{a})=Z_+(\mathfrak{a}\cap A_+)\)이다.
물론 위의 보조정리에서 등장하는 \(\mathfrak{a}\mathfrak{b}\)나 \(\sqrt{\mathfrak{a}}\), \(\sum \mathfrak{a}_i\)들은 homogeneous임이 자명하다. 그럼 첫째 결과부터 셋째 결과까지는 이미 스펙트럼에서 관찰한 결과들이며, 오직 넷째 결과만이 새롭다.
보조정리 3의 증명
-
\(\mathfrak{a}\) 혹은 \(\mathfrak{b}\)를 포함하는 homogeneous prime ideal \(\mathfrak{p}\)는 그보다 작은 homogeneous ideal \(\mathfrak{ab}\) 또한 포함하는 것이 자명하므로, 반대방향 포함관계만 보이면 충분하다. \(\mathfrak{p}\supset \mathfrak{ab}\)라 가정하자. 만일 \(\mathfrak{p}\not\supseteq \mathfrak{b}\)라 하면, \(b\not\in \mathfrak{p}\)인 \(\mathfrak{b}\)의 원소 \(b\)를 찾을 수 있다. 그럼 \(\mathfrak{b}\)가 homogeneous이므로, 이를 homogeneous element들의 합으로 분해하여
\[b=b_1+\cdots b_n,\qquad \text{$b_i\in \mathfrak{b}$ homogeneous}\]으로 쓸 수 있다. 한편, 임의의 homogeneous element \(a\in \mathfrak{a}\)에 대하여, \(ab\in \mathfrak{ab}\subseteq \mathfrak{p}\)이다. 한편 \(\mathfrak{ab}\subseteq \mathfrak{p}\)의 원소
\[ab=ab_1+\cdots+ab_n\]를 생각하면, \(\mathfrak{p}\)가 homogeneous이므로 \(ab_i\)들은 모두 \(\mathfrak{p}\)의 원소이다. 한편 앞선 가정에 의해 \(b\not\in \mathfrak{p}\)이므로, \(b_i\not\in \mathfrak{p}\)를 만족하는 \(i\)가 존재하고, 그럼 \(ab_i\)는 \(\mathfrak{p}\)에 속하는 homogeneous element이며 \(b_i\not\in \mathfrak{p}\)이므로 [가환대수학] §등급환의 국소화, ⁋보조정리 2에 의해 \(a\in \mathfrak{p}\)이다. 따라서 \(\mathfrak{a}\subseteq \mathfrak{p}\)가 성립한다.
- 이는 \(\sum \mathfrak{a}_i\)가 ideal들 \(\mathfrak{a}_i\) 각각을 모두 포함하는 ideal 중 가장 작은 것으로 정의되므로 자명하다.
- [가환대수학] §국소화의 성질들, ⁋따름정리 8.
- 정의에 의해 \(Z_+(\mathfrak{a})\subseteq Z_+(\mathfrak{a}\cap A_+)\)는 자명하므로 반대방향만 보이면 충분하다. 즉, \(\mathfrak{p}\)가 \(\mathfrak{a}\)의 양의 차수를 갖는 homogeneous element들을 모두 가지며, \(A_+\)를 통째로 포함하지는 않는 prime ideal이라 하고 \(\mathfrak{a}\subseteq \mathfrak{p}\)임을 보이자. 이를 위해서는 임의의 \(a\in \mathfrak{a}\cap A_0\)을 택했을 때, 위의 가정으로부터 \(a\) 또한 \(\mathfrak{p}\)에 석함을 보이면 충분하다.
이제 \(A_+\not\subset\mathfrak{p}\)이므로, \(\mathfrak{p}\)에 속하지 않는 homogeneous element \(f\)가 존재한다. 이제 \(af\in \mathfrak{a}\cap A_+\subseteq \mathfrak{p}\)이고, \(f\not\in \mathfrak{p}\)이므로 \(a\in \mathfrak{p}\)이다.
이 보조정리들의 결과를 보면, 첫째 결과와 둘째 결과로부터 다음을 정의할 수 있다.
정의 4 Graded ring \(A_\bullet\)이 주어졌다 하자. 임의의 homogeneous ideal \(\mathfrak{a}\)에 대하여, \(Z_+(\mathfrak{a})\) 꼴의 집합을 닫힌집합으로 갖는 \(\Proj A_\bullet\)의 (유일한) 위상을 Zariski topology라 부른다.
또, 이 보조정리의 넷째 결과에 의해, 우리는 \(\Proj A_\bullet\)을 정의할 때는 \(A_+\)에 속한 homogeneous ideal들만 고려하면 된다는 것을 안다. 이는 직관적으로도 자명한데, \(A=\mathbb{K}[\x_0,\ldots, \x_n]\)이라 두면 \(A_0\)에 들어있는 원소들은 어차피 상수함수이기 때문이다.
이제 다음을 정의한다.
정의 5 Graded ring \(A_\bullet\)의 임의의 homogeneous element \(f\)에 대하여, \(Z_+(f)\)의 \(\Proj A_\bullet\)에서의 complement \(\Proj A_\bullet\setminus Z_+(f)\)를 \(D_+(f)\)라 적는다.
다음 따름정리는 보조정리 3의 첫째 결과에 의해 바로 얻어진다.
따름정리 6 \(D_+(f)\cap D_+(g)=D_+(fg)\)가 성립한다.
뿐만 아니라 다음이 성립한다.
따름정리 7 \(D_+(f)\)들의 모임은 \(\Proj A_\bullet\)의 base를 이룬다.
증명
\(A\)의 임의의 homogeneous ideal \(\mathfrak{a}\)를 homogeneous generator들을 이용하여 \(\mathfrak{a}=\sum_{i\in I} (f_i)\)로 쓰면
\[Z_+(\mathfrak{a})=\bigcap_{i\in I} Z_+((f_i))\]이고 따라서
\[D_+(\mathfrak{a})=\bigcup_{i\in I} D_+(f_i)\]이다.
한편, 우리는 ring \(A\)의 스펙트럼 \(\Spec A\)에서, 임의의 원소 \(f\in A\)를 택하면 \(D(f)\)는 (scheme으로서) \(\Spec A_f\)와 isomorphic한 것을 살펴보았다. 비슷한 결과가 \(D_+(f)\)에 대해서도 성립한다.
보조정리 8 Graded ring \(A_\bullet\)과 임의의 homogeneous element \(f\in A_\bullet\)에 대하여, 함수 \(D_+(f) \rightarrow \Spec A_{(f)}\)를 다음의 식
\[\mathfrak{p}\mapsto \mathfrak{p}A_f\cap A_{(f)}\]으로 정의하면 이 함수는 homeomorphism이다. ([가환대수학] §등급환의 국소화, ⁋정의 5)
증명
우선 \(f\not\in \mathfrak{p}\)이므로, localization \(A \rightarrow A_f\)를 통해 \(\mathfrak{p}\)는 \(A_f\)의 prime ideal \(\mathfrak{p}A_f\)로 옮겨진다. ([가환대수학] §국소화, ⁋명제 8) 이제 주장의 우변은 inclusion \(i: A_{(f)} \rightarrow A_f\)에 의한 \(\mathfrak{p}A_f\)의 preimage이므로 이는 \(A_{(f)}\)의 prime ideal이 된다.
이제 함수로서 이 대응의 역함수 \(\Spec A_{(f)} \rightarrow D_+(f)\)를 정의하자. 임의의 prime ideal \(\mathfrak{q}\in\Spec A_{(f)}\)가 주어졌다 하고, \(A\)의 homogeneous element \(x\) 중 다음의 조건
\[\frac{x^{\deg f}}{f^{\deg x}}\in \mathfrak{q}\]을 만족하는 \(x\)들을 모은 후, 이들에 의해 생성되는 \(A\)의 homogeneous ideal \(\mathfrak{p}\)를 생각하자. 그럼 임의의 homogeneous element \(x,y\in \mathfrak{p}\)에 대하여,
\[xy\in \mathfrak{p}\iff \frac{x^{\deg f}}{f^{\deg x}}\frac{y^{\deg f}}{f^{\deg y}}\in \mathfrak{q}\]이므로 \(\mathfrak{q}\)가 prime ideal인 것으로부터 \(\mathfrak{p}\)가 prime ideal인 것을 안다. 이제 이 대응 \(\mathfrak{p}\mapsto \mathfrak{p}A_f\cap A_{(f)}\)과 \(\mathfrak{q}\mapsto \mathfrak{p}\)가 서로의 역함수인 것을 쉽게 확인할 수 있고, \(A_\bullet\)의 임의의 homogeneous ideal \(\mathfrak{a}\)에 대하여, \(D_+(f)\)의 닫힌집합 \(Z_+(\mathfrak{a})\cap D_+(f)\)는 이 함수에 의하여 \(\Spec A_{(f)}\)의 닫힌집합 \(Z(\mathfrak{a}A_f\cap A_{(f)})\)으로 옮기므로 이것이 homeomorphism이 되는 것을 안다.
그럼 이제 \(\Proj A_\bullet\)에 scheme 구조를 주는 방법은 자명하다. 다음 보조정리의 증명은 보조정리 8과 거의 유사하다.
보조정리 9 Graded ring \(A_\bullet\)과 nonzero homogeneous element \(f,g\)에 대하여, isomorphism
\[\Spec A_{(fg)}\cong D(g^{\deg f}/f^{\deg g})\subseteq \Spec A_{(f)}\]이 존재한다.
따라서, \(\Spec A_{(g)}\)의 principal open set \(D(f^{\deg g}/g^{\deg f})\subseteq \Spec A_{(f)}\)와 \(\Spec A_{(f)}\)의 principal open set \(\Spec A_{(fg)}\cong D(g^{\deg f}/f^{\deg g})\) 사이의 isomorphism이 존재한다. 이제 다음 정리는 단순한 계산이다.
정리 10 위에서 정의한 \(\Spec A_{(f)}\)들과 open subscheme들 \(D(g^{\deg f}/f^{\deg g})\), 그리고 isomorphism
\[D(f^{\deg g}/g^{\deg f})\cong \Spec A_{(fg)}\cong D(g^{\deg f}/f^{\deg g})\]들은 §스킴, ⁋보조정리 9의 조건들을 모두 만족하고, 따라서 \(\Proj A_\bullet\) 위에 유일한 scheme structure를 준다.
특히 \(\Proj A_\bullet\)은 locally ringed space이므로, 임의의 \(\mathfrak{p}\in \Proj A_\bullet\)에 대하여 stalk \(\mathscr{O}_{\Proj A_\bullet,\mathfrak{p}}\)은 local ring이다. 그런데 어차피 \(\mathfrak{p}\)는 적당한 affine open neighborhood에 넣을 수 있으므로, 본질적으로 §아핀스킴, ⁋보조정리 8과 동일한 과정으로 다음을 보일 수 있다.
보조정리 11 Graded ring \(A_\bullet\)과 임의의 \(\mathfrak{p}\in \Proj A_\bullet\)에 대하여, 다음 isomorphism
\[\mathscr{O}_{\Proj A_\bullet,\mathfrak{p}}\cong A_{(\mathfrak{p})}\]이 존재한다.
다소 주의할 것은 \(\Proj\)는 \(\Spec\)과 다르게, \(\bgr_{\mathbb{N}_{\geq 0}}\cRing^\op\)에서 \(\LRS\)로의 functor를 정의하지 않는다는 것이다. 이는 graded ring homomorphism \(\phi_\bullet:A_\bullet \rightarrow B_\bullet\)과 \(B\)의 임의의 homogeneous ideal \(\mathfrak{q}\)가 \(B_+\)를 포함하지 않더라도 그 inverse image \(\phi^{-1}(\mathfrak{q})\)는 \(A_+\)를 포함할 수도 있기 때문이다.
이제 마지막으로 우리는 맨 처음 motivation을 위해 살펴본 projective space를 대수기하의 언어로 (거의) 완전하게 옮겨본다.
예시 12 대수기하학에서, \(\mathbb{P}^n_\mathbb{K}\)는 다음의 식
\[\mathbb{P}^n_\mathbb{K}=\Proj \mathbb{K}[\x_0,\ldots, \x_n]\]으로 정의한다. 여기서 polynomial algebra \(\mathbb{K}[\x_0,\ldots, \x_n]\)은 당연히 degree를 통해 grading이 주어진 graded ring이다.
그럼 projective space에서의 \(n+1\)개의 open cover는 이 언어에서는
\[D_+(\x_i)\cong \Spec \mathbb{K}[\x_{0},\ldots, \x_{n}]_{(\x_{i})}\]으로 생각할 수 있으며, [가환대수학] §등급환의 국소화, ⁋명제 6에 의하여
\[\mathbb{K}[\x_{0},\ldots, \x_{n}]_{(\x_{i})}\cong \mathbb{K}[\x_{0/i},\ldots, \x_{n/i}]/(\x_{i/i}-1)\]이 되며, 명시적으로 이 isomorphism은 ring homomorphism
\[\mathbb{K}[\x_{0/i}, \ldots, \x_{n/i}]\rightarrow \mathbb{K}[\x_0,\ldots, \x_n]_{(\x_i)};\qquad \x_{k/i}\mapsto \frac{\x_k}{\x_i}\]에 first isomorphism theorem을 적용하여 얻어지는 것이다.
이제 임의의 \(\mathfrak{p}\in \mathbb{P}^n_\mathbb{K}\)는 어떠한 \(D_+(\x_i)\)에 포함된다. 위의 isomorphism을 통하여 \(D_+(\x_i)\)의 점 \(\mathfrak{p}\)가 \(U_i=\Spec \mathbb{K}[\x_{0/i}, \ldots, \x_{n/i}]/(\x_{i/i}-1)\)의 점 \(\mathfrak{q}\)로 옮겨졌다 하자. 그럼 이 경우에 다음의 isomorphism
\[\mathscr{O}_{\mathbb{P}^n_\mathbb{K},\mathfrak{p}}\cong \mathscr{O}_{U_i, \mathfrak{q}}\]을 기대하는 것이 당연할 것이다. 그리고 이는 물론 성립한다. ([가환대수학] §등급환의 국소화, ⁋명제 8)
참고문헌
[Har] R. Hartshorne, Algebraic geometry. Graduate texts in mathematics. Springer, 1977.
[Vak] R. Vakil, The rising sea: Foundation of algebraic geometry. Available online.

댓글남기기