스킴 사상의 성질들

앞선 글에서 우리는 scheme morphism을 살펴보는 몇 가지 관점을 살펴보았다. 이번 글에서 우리는 본격적으로 scheme morphism이 갖는 성질들을 정의한다. 우선 이들이 공유하는 다음 성질을 정의한다.

정의 1 Scheme morphism의 성질 $P$가 local on target이라는 것은 다음 두 조건이 성립하는 것이다.

1. 만일 scheme morphism $\varphi:X \rightarrow Y$가 $P$를 만족할 경우, $Y$의 임의의 open subscheme $V$에 대하여 scheme morphism $\varphi\vert_{\varphi^{-1}(V)}: \varphi^{-1}(V) \rightarrow V$ 또한 $P$를 만족한다.
2. 만일 scheme morphism $\varphi:X \rightarrow Y$에 대하여, $Y$의 open covering $\{V_j\}$가 존재하여 $\varphi\vert_{\varphi^{-1}(V_j)}: \varphi^{-1}(V_j) \rightarrow V_j$가 모두 $P$를 만족한다면 $\varphi$ 또한 그러하다.

Scheme은 affine scheme으로부터 만들어진다. Scheme morphism의 성질 $P$가 local on target이라면, scheme morphism $\varphi:X \rightarrow Y$의 target $Y$를 $\Spec B$로 가정하여도 되고, 그럼 adjoint

\[\Hom_\Sch(X, \Spec B)\cong \Hom_\cRing(B, \Gamma(X, \mathscr{O}_X))\]

를 통해 우리는 scheme morphism $X \rightarrow \Spec B$의 성질을 ring homomorphism $B \rightarrow \Gamma(X, \mathscr{O}_X)$의 성질을 통해 정의할 수 있다.

준옹골사상과 준분리사상

정의 2 Scheme morphism $\varphi: X \rightarrow Y$가 quasi-compact_준옹골이라는 것은 임의의 affine open subset $V\subseteq Y$가 주어질 때마다 $\varphi^{-1}(V)$가 quasi-compact인 것이다.

명제 3 Scheme morphism $\varphi: X \rightarrow Y$가 quasi-compact인 것은 $Y$의 임의의 quasi-compact open subset의 preimage가 quasi-compact인 것과 동치이다.

증명

임의의 affine scheme은 quasi-compact이므로 (§스펙트럼, ⁋보조정리 12) 주어진 조건이 정의 2의 조건을 함의하는 것은 당연하다.

거꾸로 quasi-compact morphism $\varphi: X \rightarrow Y$가 주어졌다 하자. 이제 $Y$의 임의의 quasi-compact open subset $V$가 주어졌다 하면, $V$를 덮는 유한히 많은 affine open subset들의 covering $\{V_j\}$가 존재하며 이들의 preimage $\varphi^{-1}(V_j)$는 모두 quasi-compact이다. 이제

\[\varphi^{-1}(V)=\varphi^{-1}\left(\bigcup_{j\in J} V_j\right)=\bigcup_{j\in J}\varphi^{-1}(V_j)\]

이고 quasi-compact set의 유한한 합집합은 다시 quasi-compact이므로 원하는 결과를 얻는다.

그럼 명제 3의 동치로부터, 임의의 quasi-compact morphism의 합성은 다시 quasi-compact임을 안다. 뿐만 아니라 다음이 성립한다.

명제 4 Noetherian scheme $X$에 대하여, scheme morphism $\varphi: X \rightarrow Y$는 항상 quasi-compact이다.

증명

임의의 affine open subset $V\subseteq Y$가 주어졌다 하고, $\varphi^{-1}(V)$가 quasi-compact임을 보여야 한다. 그런데 [위상수학] §차원, ⁋명제 12와 [위상수학] §차원, ⁋명제 13의 첫째 결과로부터 noetherian인 위상공간의 임의의 부분공간은 quasi-compact이다.

비슷하게 우리는 quasi-separated morphism을 정의한다. 이를 위해서는 quasi-separated scheme을 먼저 정의해야 한다.

정의 5 Scheme $X$가 quasi-separated_준분리인 것은 $X$의 임의의 두 quasi-compact open subset의 교집합이 다시 quasi-compact인 것이다. Scheme morphism $\varphi: X \rightarrow Y$가 quasi-separated인 것은 임의의 affine open set $V\subseteq Y$에 대하여, $\varphi^{-1}(V)$가 quasi-separated인 것이다.

그럼 다음이 성립한다.

명제 6 Locally noetherian scheme은 항상 quasi-separated이다.

증명

Locally noetherian scheme $X$의 임의의 두 affine open subset $V_1=\Spec B_1, V_2=\Spec B_2$가 주어졌다 하고 $V_1\cap V_2$가 quasi-compact임을 보여야 한다.

우선 $X$가 locally noetherian이므로, $X$를 noetherian ring들의 스펙트럼 $\Spec A_i$로 덮을 수 있다. 이제 각각의 $i$에 대하여, §스킴의 위상구조, ⁋보조정리 11에 의하여 $U_i\cap V_1$을 noetherian ring들의 스펙트럼 $\Spec (A_i)_g$들로 덮을 수 있다. 이들을 모두 모으면 $V_1$을 noetherian ring들의 스펙트럼들로 덮을 수 있으며, §스펙트럼, ⁋보조정리 12에 의해 $V_1=\Spec B_1$은 유한히 많은 noetherian ring들의 스펙트럼으로 덮인다. 따라서 §스킴의 위상구조, ⁋보조정리 13에 의해 $B_1$은 noetherian ring이고 따라서 $V_1=\Spec B_1$은 noetherian이다. 다시 [위상수학] §차원, ⁋명제 12와 [위상수학] §차원, ⁋명제 13의 첫째 결과로부터 noetherian인 위상공간의 임의의 부분공간은 quasi-compact이므로, 특히 $V_1\cap V_2$ 또한 quasi-compact이다.

그럼 quasi-compactness와 quasi-separatedness는 정의 1의 성질을 만족할 뿐만 아니라, 다음 명제에서 확인할 수 있듯이 affine-local on target이다. (§스킴의 위상구조, ⁋정의 9)

명제 7 Scheme morphism $\varphi: X \rightarrow Y$에 대하여 다음이 성립한다.

1. 만일 $Y$의 affine open covering $\{V_j\}$가 존재하여 각각의 $\varphi^{-1}(V_j)$가 quasi-compact라면, $\varphi$는 quasi-compact이다.
2. 만일 $Y$의 affine open covering $\{V_j\}$가 존재하여 각각의 $\varphi^{-1}(V_j)$가 quasi-separated라면, $\varphi$는 quasi-separated이다.

증명

1. $Y$의 임의의 affine open subset $V$가 주어졌다 하자. 그럼 §스킴의 위상구조, ⁋보조정리 11에 의하여 $V$와 $V_j$ 각각에서 principal open set이 되는 열린집합들로 $V\cap V_j$를 덮을 수 있고, 이를 모든 $j$에 대해 고려한 후 $V$의 quasi-compactness를 사용하면 이러한 것들 중 유한히 많은 것만 택할 수 있다. 이를 $V=\bigcup W_l$이라 하자.
   한편 각각의 $j$에 대하여, $\varphi^{-1}(V_j)$는 quasi-compact이므로, 이를 유한히 많은 affine open subset들 $U_{jk}$들로 덮을 수 있고, 이제 $\varphi^{-1}(W_l)\cap U_{jk}$는 §스펙트럼, ⁋명제 8에 의해 $U_{jk}$의 principal open set이므로 $\varphi^{-1}(W_l)$ 각각을 affine open set들의 유한한 합집합으로 표현할 수 있고, 따라서 $\varphi^{-1}(V)$도 affine open set들의 유한한 합집합으로 표현할 수 있다. 이제 quasi-compact space의 유한한 합집합은 quasi-compact이므로 원하는 결과를 얻는다.
2. 이 또한 첫째 결과와 마찬가지 방식으로, §스킴의 위상구조, ⁋보조정리 11를 사용하여 임의의 affine open subset $V=\Spec B$를 그 preimage가 quasi-separated인 principal open subset들로 덮은 후 증명을 하면 된다.

아핀사상

우리는 adjoint

\[\Hom_\Sch(X, \Spec B)\cong\Hom_\cRing (B, \Gamma(X, \mathscr{O}_X))\]

에서, 특별히 $X=\Spec A$인 경우

\[\Hom_\Sch(\Spec A,\Spec B)\cong\Hom_\cRing (B, A)\]

가 성립하는 것을 안다. (§아핀스킴, ⁋명제 11) 따라서, 위와 같이 affine-local on target인 스킴 사상의 성질을 살펴볼 때에는, $Y$의 임의의 affine open subset $V\cong\Spec B$에 대하여 $U=\varphi^{-1}(V)$도 $X$의 open subscheme $U\cong \Spec A$이고, 따라서 $\varphi\vert_U: U \rightarrow V$가 affine scheme들 사이의 morphism이 되어 이 성질을 ring homomorphism

\[(\varphi\vert_U)^\sharp(V): \mathscr{O}_V(V) \rightarrow \varphi^\ast \mathscr{O}_U(V)=\mathscr{O}_U(U)\]

으로부터 얻어낼 수 있으면 좋을 것이다. 그러나 물론 임의의 scheme morphism $\varphi: X \rightarrow Y$에 대하여, $Y$의 affine open subset의 preimage가 affine이 되지는 않는다. (§스킴, ⁋예시 8)

정의 8 Scheme morphism $\varphi: X \rightarrow Y$가 affine이라는 것은 $Y$의 임의의 affine open subset $V$에 대하여 $\varphi^{-1}(V)$가 $X$의 affine open subset인 것이다.

그럼 affine morphism의 합성이 affine인 것은 자명하다. 뿐만 아니라 이 성질은 정의 1의 성질 또한 만족하는데, 이에 대한 증명은 다소 길어지는 감이 있어 생략한다.

명제 9 Scheme morphism $\varphi:X \rightarrow Y$에 대하여, 만일 $Y$의 affine open covering $\{V_j\}$가 존재하여 각각의 $\varphi^{-1}(V_j)$가 affine라면, $\varphi$는 affine이다.

유한사상, 정수형사상과 유한형사상

정의 10 Scheme morphism $\varphi:X \rightarrow Y$가 finite_유한인 것은 $\varphi$가 affine이고, $Y$의 임의의 affine open subset $V$에 대하여, ring homomorphism

\[(\varphi\vert_{\varphi^{-1}(V)})^\sharp(V): \mathscr{O}_V(V) \rightarrow \varphi^\ast \mathscr{O}_{\varphi^{-1}}(V)\]

이 finite ring homomorphism인 것이다. ([가환대수학] §정수적 확장, ⁋정의 3)

이해를 돕기 위해 affine open subset $V\subseteq Y$를 $\Spec B$라 쓰자. 그럼 $\varphi$가 affine이라는 가정으로부터 $U=\varphi^{-1}(V)$는 $X$의 affine open subset이고 따라서 $U\cong\Spec A$이도록 하는 $A$가 존재한다. 이러한 identification을 통해, scheme morphism $\varphi\vert_U: U \rightarrow V$는 스펙트럼 사이의 morphism $\Spec A \rightarrow \Spec B$와 같은 것이고, 이제 $\varphi$가 finite이라는 것은 이 morphism에 해당하는 ring homomorphism $B \rightarrow A$가 finite인 것이다. 비슷하게 다음을 정의한다.

정의 11 Scheme morphism $\varphi:X \rightarrow Y$가 integral_정수형인 것은 $\varphi$가 affine이고, $Y$의 임의의 affine open subset $V$에 대하여, ring homomorphism

\[(\varphi\vert_{\varphi^{-1}(V)})^\sharp(V): \mathscr{O}_V(V) \rightarrow \varphi^\ast \mathscr{O}_{\varphi^{-1}(V)}(V)\]

이 integral ring homomorphism인 것이다. ([가환대수학] §정수적 확장, ⁋정의 3)

이제 그 정의로부터 finite morphism과 integral morphism이 합성에 대해 닫혀있다는 것을 안다. 또, 이들이 정의 1의 조건을 만족하는 것은 [가환대수학] §정수적 확장, ⁋명제 14와 [가환대수학] §정수적 확장, ⁋명제 15로부터 알 수 있으므로 이들은 모두 affine-local on target이다.

우리는 [가환대수학] §정수적 확장, ⁋보조정리 4에 의해 임의의 finite morphism은 integral인 것을 안다. 이제 이 보조정리를 완전하게 대수기하의 언어로 서술하기 위해서는 finite type morphism을 정의해야 한다.

정의 12 Scheme morphism $\varphi:X \rightarrow Y$가 locally of finite type_{국소적으로 유한형}인 것은 $Y$의 임의의 affine open subset $V$와 $\varphi^{-1}(V)$의 임의의 affine open subset $U$에 대하여,

\[(\varphi\vert_{U})^\sharp(V): \mathscr{O}_V(V) \rightarrow \varphi^\ast \mathscr{O}_{\varphi^{-1}(V)}(V)\]

이 finite type인 것이다. ([가환대수학] §정수적 확장, ⁋정의 3)

역시 위와 마찬가지로, $V\cong \Spec B$라 하고 $U\cong\Spec A\subseteq \varphi^{-1}(V)$라 하자. 그럼 scheme morphism $\varphi\vert_U: U \rightarrow V$를 $\Spec A \rightarrow \Spec B$로 볼 수 있고, 이에 대응하는 ring homomorphism $B \rightarrow A$가 finite type일 것을 요구하는 것이다. 그럼 finite type morphism은 다음과 같이 정의된다.

정의 13 Scheme morphism $\varphi:X \rightarrow Y$가 morphism of finite type_{유한형사상}이라는 것은 $\varphi$가 quasi-compact morphism locally of finite type인 것이다.

정의로부터 morphism of locally finite type은 affine-local on target임이 명확하다. 또, quasi-compact morphism은 명제 7로부터 affine-local on target이므로 finite type morphism 또한 affine-local on target이다.

그럼 [가환대수학] §정수적 확장, ⁋보조정리 4에 의해 다음이 성립한다.

명제 14 Scheme morphism $\varphi:X \rightarrow Y$가 finite인 것은 $\varphi$가 integral morphism (locally) of finite type인 것과 동치이다.

증명

한쪽 방향은 자명하다. 반대쪽 방향은 우선 $\varphi$가 integral이라는 가정으로부터 임의의 affine open subset $V\subseteq Y$에 대하여 $\varphi^{-1}(V)$가 $X$의 affine open subset임을 알고, 이렇게 얻어진 ring map에 [가환대수학] §정수적 확장, ⁋보조정리 4를 적용하면 된다.

위의 명제에서 $\varphi$는 integral morphism이므로 affine morphism이고, 따라서 quasi-compact morphism이므로 (§스펙트럼, ⁋보조정리 12) $\varphi$가 finite type이든, locally finite type이든 똑같은 가정이 된다.

예시 15 이번 절에서 살펴본 morphism들의 예시를 살펴보자. Affine scheme들의 세상에서 이는 그저 [가환대수학] §정수적 확장, ⁋정의 3의 예시들을 보는 것에 지나지 않는다. 이번 예시의 목적은 이들에 기하학적인 직관을 부여하는 것이다.

우선 algebraically closed field $\mathbb{k}$에 대하여, ring map $\iota:\mathbb{k}[\x] \rightarrow \mathbb{k}[\x,\y]$를 생각하면 $\mathbb{k}[\x,\y]$는 $\mathbb{k}[\x]$-algebra로서 하나의 원소 $\y$에 의해 생성되므로 finite type ring homomorphism이지만, $\mathbb{k}[\x]$-module로서는 유한하게 생성되지 않으므로 finite ring homomorphism은 아니다.

이제 이에 대응되는 scheme morphism $\Spec\iota: \Spec \mathbb{k}[\x,\y] \rightarrow\Spec \mathbb{k}[\x]$를 생각하자. 이는 임의의 prime ideal $\mathfrak{p}\subset \mathbb{k}[\x,\y]$를 받아 $\mathbb{k}[\x]$의 prime ideal $\mathfrak{p}\cap \mathbb{k}[\x]$를 내놓는 함수이다. 이는 기하적으로는 affine plane $\mathbb{A}^2_\mathbb{k}$의 점 $(x,y)$를 affine line $\mathbb{A}^1_\mathbb{k}$의 점 $x$에 대응시키는 함수이다.

이와 관련된 finite morphism의 예시로는 위의 ring homomorphism $\iota:\mathbb{k}[\x]\rightarrow \mathbb{k}[\x,\y]$에 projection map $\pi:\mathbb{k}[\x,\y] \rightarrow \mathbb{k}[\x,\y]/(\x-\y^2)$을 합성한 것이 있다. 그럼 $\mathbb{k}[\x,\y]/(\x-\y^2)$은 $\mathbb{k}[\x]$-module로서 $1$과 $\y$에 의해 생성되므로 $\phi:\mathbb{k}[\x] \rightarrow \mathbb{k}[\x,\y]/(\x-\y^2)$은 finite morphism이다.

한편 우리는 ring homomorphism $\pi:A \rightarrow A/\mathfrak{a}$는 기하적으로 $\mathfrak{a}$가 정의하는 닫힌집합의 inclusion에 해당하는 것을 안다. 따라서 합성

\[\phi: \mathbb{k}[\x] \rightarrow \mathbb{k}[\x,\y] \rightarrow \mathbb{k}[\x,y]/(\x-\y^2)\]

이 정의하는 scheme morphism

\[\Spec\phi: \Spec \frac{\mathbb{k}[\x,\y]}{(\x-\y^2)}\rightarrow \Spec \mathbb{k}[\x,\y] \rightarrow \Spec\mathbb{k}[\x]\]

은 기하적으로 $\x=\y^2$의 zero set $Z(\x-\y^2)$에서 $x$축으로의 projection으로 볼 수 있다.

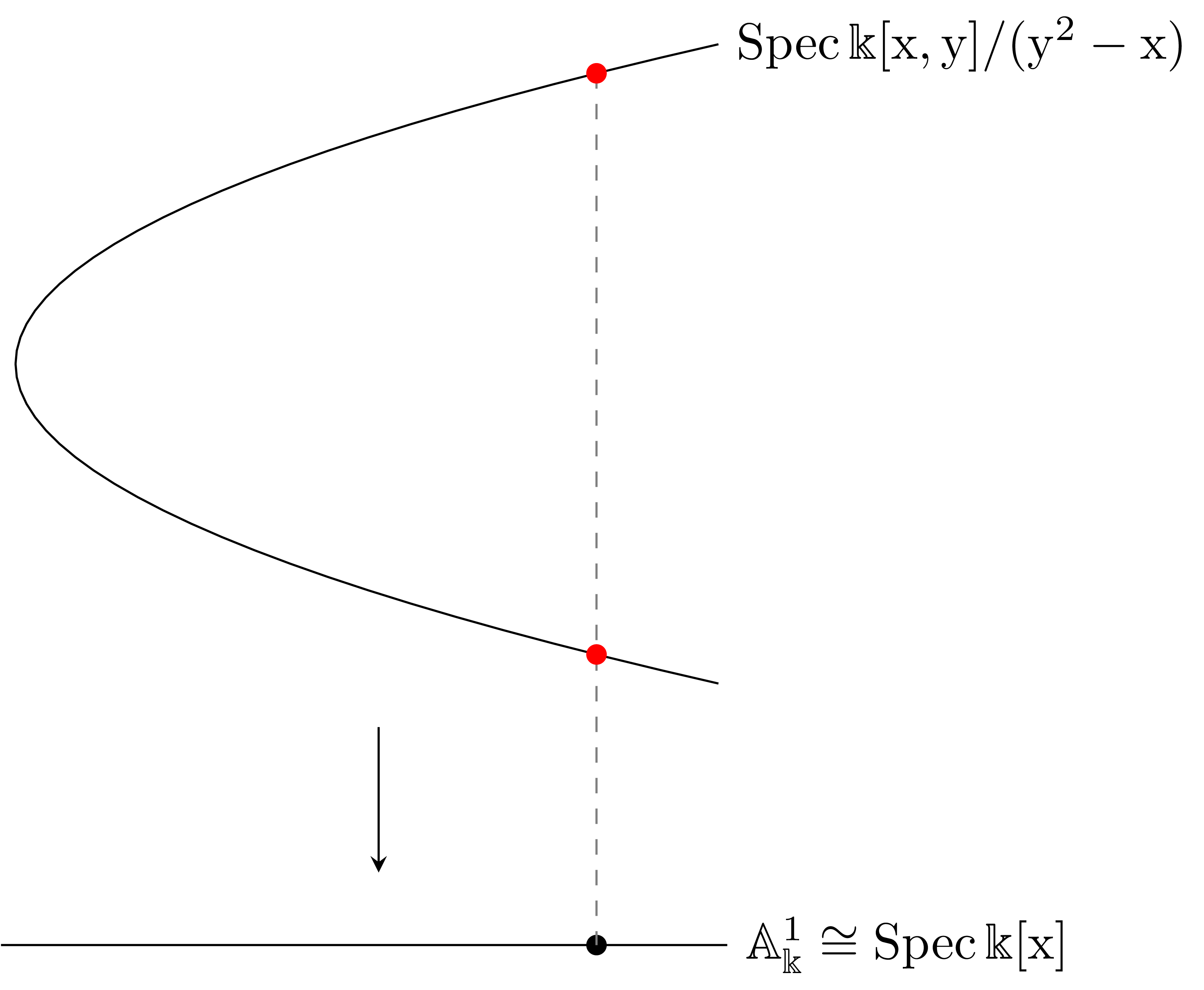
이 두 예시의 기하학적인 차이는 꽤나 명확하다. 첫 번째 예시의 경우, target의 한 점에서의 fiber가 무한집합인 반면 두 번째 예시의 경우 한 점에서의 fiber가 유한집합이다. 대수적으로 이는 target $\mathbb{A}_\mathbb{k}^1$의 임의의 점 $\mathfrak{p}=(\x-a)$를 가져왔을 때, 임의의 $\mathfrak{q}_b=(\x-a, \y-b)\in \mathbb{A}_\mathbb{k}^2$는 $(\Spec\iota)(\mathfrak{q}_b)=\mathfrak{p}$를 만족하는 반면, 두 번째 예시에서는 오직 두 개의 점 $\mathfrak{q}_+=(\x-a, \y-\sqrt{a})$와 $\mathfrak{q}_-=(\x-a, \y+\sqrt{a})$만이 $(\Spec\phi)(\mathfrak{q}_\pm)=\mathfrak{p}$를 만족하는 것으로 확인할 수 있다.

이와 같이, finite type morphism은 기하적으로는 fiber가 유한차원인 것과 관련이 있고, finite morphism은 fiber가 유한집합인 것과 관련이 있다.

아직은 위의 예시 15과 같은 상황에서 scheme morphism의 fiber를 계산하기 위해서는 그때그떄 상황에 맞추어 우직하게 계산을 해 나가는 수밖에 없지만, 나중에 fiber product를 계산하고 나면 조금 더 정형화된 방식을 사용할 수 있게 된다. 그 떄를 위해 다음을 정의한다.

정의 16 Scheme morphism $\varphi: X \rightarrow Y$가 quasi-finite_준유한인 것은 $\varphi$가 morphism of finite type이고 임의의 $y\in Y$에 대하여 집합 $\varphi^{-1}(y)$가 항상 유한집합인 것이다.

그럼 예시 15에서의 finite morphism에 대한 기하학적 직관은 항상 참이다. 즉, 임의의 finite morphism은 항상 quasi-finite이다. 이는 지금 당장 증명하는 것도 가능하지만, fiber product를 정의하고 난 후로 미룬다.

마지막으로 다음을 정의한다.

정의 17 Scheme morphism $\varphi: X \rightarrow Y$가 locally of finite presentation_{국소유한표시사상}이라는 것은 $Y$의 임의의 affine open subset $V\cong \Spec B$가 주어질 때마다, $\varphi^{-1}(V)$의 covering $\varphi^{-1}(V)=\bigcup \Spec A_i$가 존재하여 $B \rightarrow A_i$가 모두 finitely presented인 것이다. 만일 scheme morphism $\varphi:X \rightarrow Y$가 quasi-compact, quasi-separated, locally of finite presentation이라면 $\varphi$가 morphism of finite presentation_{유한표시사상}이라 부른다.

대부분의 경우 우리는 모든 scheme들이 locally noetherian인 경우를 생각하고, 이 경우 [가환대수학] §기본 개념들, ⁋명제 9에 의하여 이 개념은 새로운 것이 아니다.