접다발과 여접다발

벡터다발

이제 우리는 벡터장을 정의해야 하는데, \(C^\infty\) 벡터장과 같은 개념을 정의하기 위해서는 벡터다발의 개념을 먼저 정의하는 것이 좋다. 우선 위상공간 위에 정의된 벡터다발을 먼저 정의하자.

정의 1 위상공간 \(B\) 위에 정의된 vector bundle_벡터다발은 \(\pi:E \rightarrow B\)는 다음과 같이 정의된 대상이다.

• Total space \(E\)와 base space \(B\)는 모두 위상공간이며, \(\pi:E \rightarrow B\)는 연속인 전사함수다.
• 각각의 \(b\in B\)에 대하여, \(E_b=\pi^{-1}(b)\)는 \(k\)차원 벡터공간의 구조를 갖는다.
• 각각의 \(b_0\in B\)마다 적당한 열린근방 \(U\subseteq B\), 그리고 homeomorphism \(h:U\times\mathbb{R}^k \rightarrow\pi^{-1}(U)\)가 존재하여, 모든 \(b\in U\)마다 \(x\mapsto h(b,x)\)가 isomorphism이도록 할 수 있다.

이 때 \(k\)를 vector bundle \(E\rightarrow B\)의 rank라 부른다. 셋째 조건의 homomorphism \(h\)를 local trivialization이라 부르며, 만일 \(U=B\)로 둘 수 있다면 \(E\)를 trivial vector bundle이라 부른다.

이와 유사하게 manifold 위에도 vector bundle을 정의할 수 있다. 이를 위해서는 \(E\)와 \(B\)를 모두 manifold로, \(\pi\)를 \(C^\infty\)인 전사함수로 바꾸고, 셋째 조건을

각각의 \(b_0\in B\)마다 적당한 coordinate system \(U\subseteq B\), 그리고 diffeomorphism \(h:U\times\mathbb{R}^k\rightarrow\pi^{-1}(U)\)가 존재하여, 모든 \(b\in U\)마다 \(x\mapsto h(b,x)\)가 isomorphism이도록 할 수 있다.

으로 바꾸면 된다.

접다발

Vector bundle의 대표적인 예시는 tangent bundle이다.

예시 2 (Tangent bundle) 집합 \(TM\)을

\[TM=\bigsqcup_{p\in M} T_pM\]

으로 정의하자. 그럼 자연스러운 projection map \(\pi:TM\rightarrow M\)이 존재한다. \(TM\)을 vector bundle로 보기 위해서는 여기에 manifold 구조를 주어야 한다.

우선 \(TM\) 위에 coorindate system을 정의하자. 임의의 coordinate system \((U,\varphi)\)에 대하여, 함수 \(\tilde{\varphi}:\pi^{-1}(U)\rightarrow\mathbb{R}^m\times\mathbb{R}^m\)을 다음의 식

\[\tilde{\varphi}(v)=\bigl(x^1(\pi(v)), \ldots, x^m(\pi(v)), dx^1(v),\ldots, dx^m(v)\bigr)\]

으로 정의하자. 그럼 \(\tilde{\varphi}\)는 \(\pi^{-1}(U)\)에서 \(\mathbb{R}^{2m}\)의 열린집합 \(\varphi(U)\times\mathbb{R}^m\)으로의 bijection이다.

이들은 \(C^\infty\)-compatible이다. 또 다른 coordinate system \((V,\psi)\), \(\psi=(y^j)_{j=1}^m\)가 주어졌다 하고, \(\tilde{\psi}\)를 위와 같이 정의하자. 그럼 \(\pi^{-1}(U)\cap\pi^{-1}(V)=\pi^{-1}(U\cap V)\) 위에서

\[\begin{aligned}(\tilde{\psi}\circ\tilde{\varphi}^{-1})(p^1, \ldots, p^m, v^1, \ldots, v^m)&=\tilde{\psi}\left(\varphi^{-1}(p), \sum v^i\frac{\partial}{\partial x^i}\bigg|_{\varphi^{-1}(p)}\right)\end{aligned}\]

이다. 여기에서 \(v=\sum v^i\frac{\partial}{\partial x^i}\)라 하면 우변은 간단히

\[\left((\psi\circ\varphi^{-1})(p), dy^1(v), \ldots, dy^m(v)\right)\]

로 쓸 수 있다. 이제 임의의 \(j\)에 대하여

\[dy^j\left(\sum v^i\frac{\partial}{\partial x^i}\bigg|_{\varphi^{-1}(p)}\right)=\sum_{i=1}^m v^i\frac{\partial y^j}{\partial x^i}\bigg|_{\varphi^{-1}(p)}\]

가 된다. 따라서, 위의 transition map \(\tilde{\psi}\circ\tilde{\varphi}^{-1}\)의 각 성분들이 \(C^\infty\)이므로 \(\tilde{\psi}\circ\tilde{\varphi}^{-1}\)도 \(C^\infty\)이다.

한편 \(TM\)의 위상은 다음의 집합들

\[\{\tilde{\varphi}^{-1}(W)\mid \text{$W$ open in $\mathbb{R}^{2m}$, $(U,\varphi)\in\mathcal{A}$}\}\]

을 basis로 하여 얻어진다. \(W=\mathbb{R}^{m}\)으로 두면 위의 집합에 의해 만들어지는 위상에서 \(\pi^{-1}(U)\)들이 모두 열린집합임을 확인할 수 있고, 이 위상이 \(2m\)차원의 topological manifold를 만든다는 것도 확인할 수 있다.

이제 남은 것은 \(TM\)에서의 local trivialization 뿐이다. 임의의 coordinate system \((U,\varphi)\)에 대하여, \(\phi:\pi^{-1}(U)\rightarrow U\times\mathbb{R}^m\)을 이번에는 다음의 식

\[v|_p\mapsto (p, dx^1(v),\ldots, dx^m(v))\]

으로 정의하면 된다. 고정된 \(\pi^{-1}(p)\) 위에서 \(\phi\)가 벡터공간 사이의 isomorphism이 되는 것은 자명하고, 또 임의의 \(v_x\)에 대하여 \((\pi\circ\phi)(x,v)=x\)임도 자명하다. \(\phi\)가 diffeomorphism이 된다는 것은

\[\tilde{\varphi}=(\varphi\times\id_{\mathbb{R}^m})\circ\phi\]

이고, 이 식에서 \(\phi\)를 제외한 두 함수가 모두 diffeomorphism이기 때문에 성립한다.

특별히 \(TM\)이 trivial bundle일 경우, \(M\)을 parallelizable manifold라 부른다.

Smooth functors

Tangent bundle \(TM\)이 중요한 것은 manifold 위에 정의된 대다수의 vector bundle이 \(TM\)으로부터 정의되기 때문이다. 가령 cotangent bundle \(T^\ast M\)은 각각의 \(p\in M\)마다 tangent space의 dual space인 cotangent space \(T_p^\ast M\)이 붙어있는 vector bundle이다. 이와 비슷하게, 각 점 \(p\)마다 선형대수에서의 연산들(예시 5)을 통해 다양한 vector bundle이 정의된다.

원래대로라면 이들을 정의할 때마다 이들이 vector bundle의 조건을 만족한다는 것을 보여야 하지만, [Mil]에 조금 더 근본적인 방식이 있다.

정의 3 두 vector bundle \(E\rightarrow B\), \(E'\rightarrow B'\)가 주어졌다 하자. 그럼 \(E \rightarrow B\)에서 \(E' \rightarrow B'\)의 bundle map_{벡터다발 준동형사상}은 다음의 diagram

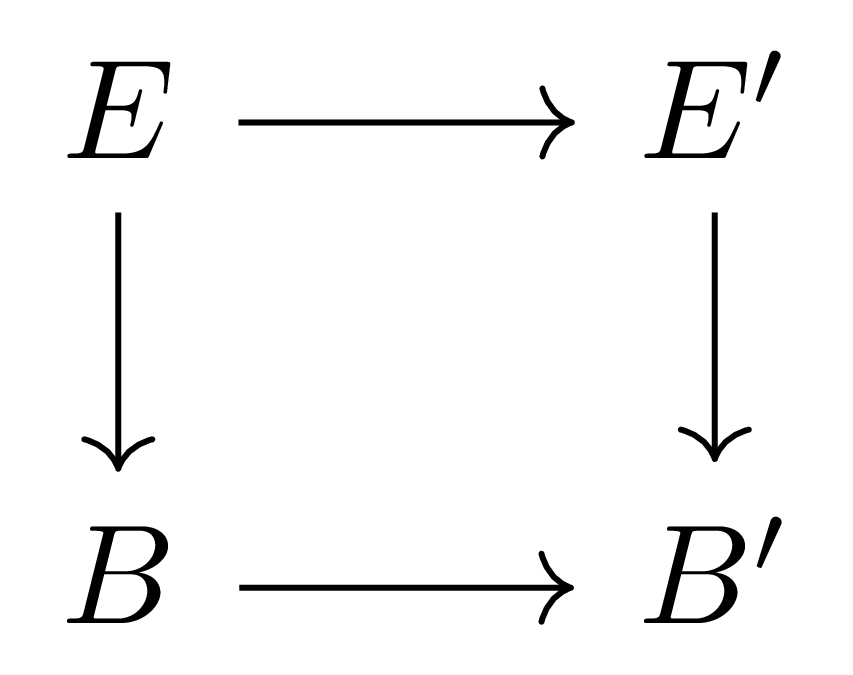
을 commute하도록 하는 쌍 \(E\rightarrow E', B \rightarrow B'\) 중, \(E_b\rightarrow E'_{b'}\)가 isomorphism인 것들을 의미한다.

이제 morphism들이 isomorphism으로 구성된 유한차원 \(\mathbb{R}\)-벡터공간들의 category \(\mathbf{FVect}_\text{iso}\)를 생각하자. 그럼 \(\mathbf{FVect}_\text{iso}\times\mathbf{FVect}_\text{iso}\)는

• 유한차원 벡터공간들의 pair \((V,W)\)들이 object,
• 유한차원 벡터공간들 사이의 isomorphism들의 pair \((V,W)\overset{(f,g)}{\longrightarrow}(V',W')\)가 morphism

인 category이다. 따라서 \(\mathbf{FVect}_\text{iso}\times\mathbf{FVect}_\text{iso}\)에서 \(\mathbf{FVect}_\text{iso}\)로의 functor \(F\)는 \((V,W)\)를 받아 \(\mathbb{R}\)-벡터공간 \(F(V,W)\)를, \((f,g)\)를 받아 isomorphism \(F(f,g)\)를 내놓아야 한다.

정의 4 Functor \(F:\mathbf{FVect}_\text{iso}\times\mathbf{FVect}_\text{iso}\rightarrow \mathbf{FVect}_\text{iso}\)이 smooth functor_{매끄러운 함자}라는 것은 \(F(f,g)\)가 \(f,g\)에 대해 smooth하게 의존하는 것이다.

만일 \(f\in\Hom(V,V'), g\in\Hom(W,W')\)라면 \(F(f,g)\in\Hom(F(V,W),F(V',W'))\)이다. 이들은 모두 벡터공간이므로 §미분다양체의 예시들, ⁋예시 2와 같은 미분구조가 주어져 있고, 이를 통해 위의 정의를 적용할 수 있다. 또, 어렵지 않게 이 정의를 일반적인 \(k\)-fold product

\[\mathbf{FVect}_\text{iso}\times\cdots\times\mathbf{FVect}_\text{iso}\rightarrow \mathbf{FVect}_\text{iso}\]

으로도 확장할 수 있다.

예시 5 \(\Hom(-,-)\)은 smooth functor이다. 임의의 두 isomorphism \(f:V\rightarrow V'\), \(g:W\rightarrow W'\)이 주어져 있다 하자. 그럼 \(\Hom(f,g)\)는 \(\Hom(V,W)\)에서 \(\Hom(V',W')\)로의 functor이며 아래 diagram

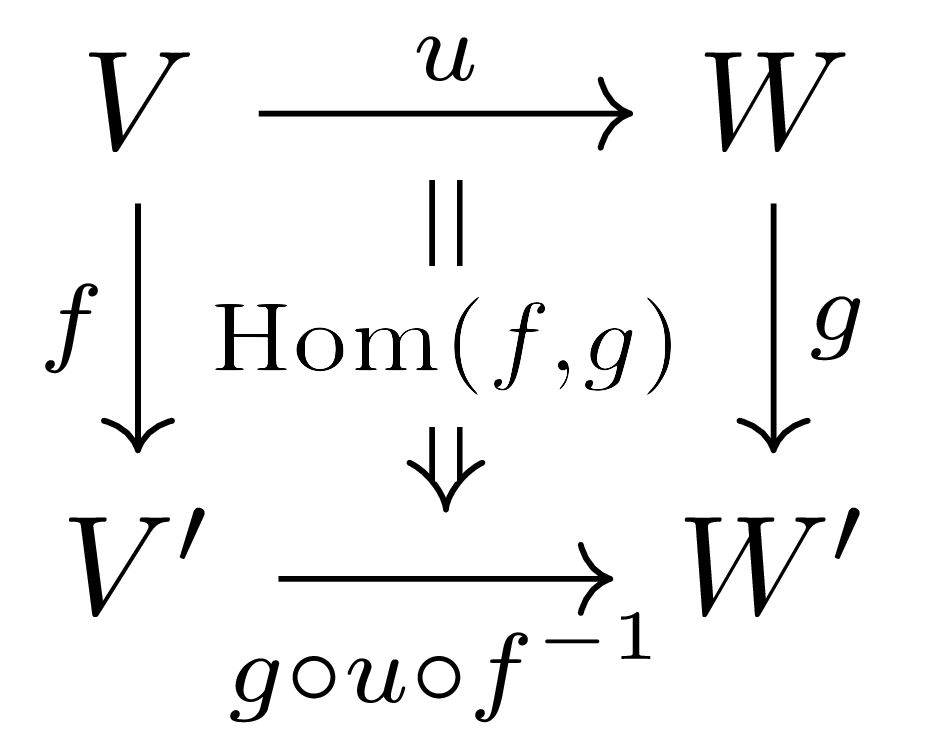
을 commute하도록 한다. 이를 식으로 쓰면 \(\Hom(f,g)(u)=g\circ u\circ f^{-1}\)이라 할 수 있다. \(\Hom(f,g)\)가 \(g\)에 smooth하게 의존한다는 것을 쉽게 확인할 수 있다. 대응 \(g\mapsto \Hom(f,g)\)를 생각하자. 그럼 \(\Hom(W,W')\)의 basis \(w_i^j\)에 대하여,

\[(g+tw_i^j)\circ u\circ f^{-1}=g\circ u\circ f^{-1}+tw_i^j\circ u\circ f^{-1}\]

가 모든 \(u\)에 대해 성립하므로 이 대응의 \(w_i^j\)-방향미분은 \(u\mapsto w_i^j\circ u\circ f^{-1}\)가 되어 연속이다. 뿐만 아니라 이 논증은 \(g\) 자리에 어떠한 linear map를 집어넣어도 성립하므로, 이로부터 \(g\mapsto\Hom(f,g)\)의 임의의 고차 방향미분이 항상 연속이라는 것을 안다. 즉, \(g\mapsto\Hom(f,g)\)는 \(C^\infty\)이다. 이 대응이 \(f\)에도 smooth하게 의존한다는 것은 \(g\)보다는 번거롭지만, \(f\)가 isomorphism이라는 것으로부터 \(t\)를 충분히 작게 택하여 \(f+tw_i^j\)가 invertible하도록 할 수 있고, 이후 위의 논증을 반복하면 된다.

다음은 모두 smooth functor의 예시들이다.

• Dual functor \((-)^\ast\) ([선형대수학] §쌍대공간),
• \(k\)-th tensor functor \(\mathcal{T}^k(-)\) ([다중선형대수] §텐서대수),
• \(k\)-th symmetric functor \(\mathcal{S}^k(-)\) ([다중선형대수] §텐서대수),
• \(k\)-th exterior functor \(\bigwedge\nolimits^k(-)\) ([다중선형대수] §텐서대수),
• Tensor product \(-\otimes -\),
• Direct sum \(-\oplus-\).

다음 정리의 증명은 [MS]의 정리 3.6에서 찾을 수 있다.

정리 6 임의의 smooth functor \(F:(\mathbf{FVect}_\text{iso})^n\rightarrow \mathbf{FVect}_\text{iso}\), 그리고 공통된 base space \(B\)를 갖는 \(n\)개의 vector bundle들 \(E_i\rightarrow B\)들이 주어졌다 하자. 그럼 각각의 \(b\in B\)에서의 fiber가

\[E_b=F((E_1)_b,\ldots,(E_n)_b)\]

로 주어진 vector bundle \(E\rightarrow B\)가 존재한다.

위와 같은 과정으로 얻어지는 vector bundle \(E\)를 간단히 \(F(E_1,\ldots, E_n)\)과 같이 표기한다.

여접다발

임의의 manifold \(M\)과 tangent bundle \(E=TM\rightarrow M\), 그리고 dual functor \((-)^\ast\)에 위의 정리 6을 적용하면 다음을 얻는다.

정의 7 Manifold \(M\) 위에 정의된 cotangent bundle_여접다발은 정리 6에 의해 얻어진 vector bundle \((TM)^\ast\)을 의미한다. Cotangent space \(T_p^\ast M\)의 표기에 맞추어 이를 \(T^\ast M\)으로 표기한다.

\(T^\ast M\)은 점 \(p\)마다 벡터공간 \(T_p^\ast M\)이 붙어있는 공간이다. 이 때 \(T_p^\ast M\)은 벡터공간 \(T_pM\)의 dual space, 곧 \(T_pM\)의 벡터를 하나 받아 실수를 내놓는 linear map들의 공간이다. 또 다른 smooth functor들을 적용하여 얻어지는 vector bundle들은 조만간 다시 살펴보게 된다.

---

참고문헌

[MS] J.W. Milnor and J.D. Stasheff, Characteristic classes, Princeton university press, 1974.

---