벡터장
앞선 글에서 벡터다발을 정의한 것은 나중에 사용하기 위한 것이기도 하지만, 당장은 벡터장을 정의하기 위해 필요했기 때문이다.
정의 1 임의의 vector bundle $\pi:E\rightarrow M$에 대하여, $\pi\circ\sigma=\id_M$을 만족하는 $\sigma:M\rightarrow E$를 vector bundle $E\rightarrow M$의 section이라 부른다.
이 정의는 $\sigma$가 각 점 $p$를 받아 $E_p$의 원소를 내놓는 함수라는 이야기에 불과하다. 한편, $E$ 또한 manifold이므로 임의의 section $\sigma:M\rightarrow E$는 두 manifold 사이의 함수이고, 따라서 $\sigma$의 smoothness가 잘 정의된다. Vector bundle $E\rightarrow M$의 smooth section들의 모임을 $\Gamma(E)$로 적는다.
특별히 tangent bundle $\pi:TM\rightarrow M$의 section $X$을 벡터장vector field이라 부르고, 종종 점 $p$에서의 $X$의 함숫값을 $X_p$로 적는다. 그럼 $X_p\in T_pM$이므로, 점 $p$ 근방에서 정의된 함수 $f$에 대하여 실수 $X_p(f)$가 잘 정의된다. 특별히 $f$가 열린집합 $U$ 위에서 정의되었다면, 점 $p\in U$를 받아 실수 $X_p(f)$를 내놓는 함수 $U\rightarrow\mathbb{R}$을 $X(f)$로 표기한다.
명제 2 Manifold $M$ 위에서 정의된 벡터장 $X$를 생각하자. 다음이 모두 동치이다.
- $X$가 $C^\infty$이다.
-
임의의 coordinate system $(U,\varphi)$, $\varphi=(x^i)_{i=1}^m$에 대하여, 다음의 식
\[(X|_U)_p=\sum_{i=1}^m a^i(p)\frac{\partial}{\partial x^i}\bigg|_p\]으로 정의된 함수 $a^i:U\rightarrow\mathbb{R}$들이 모두 $U$에서 정의된 $C^\infty$ 함수들이다.
- 임의의 열린집합 $V\subseteq M$과 $V$ 위에서 정의된 $C^\infty$ 함수 $f:V\rightarrow\mathbb{R}$에 대하여, $X(f)$ 또한 $C^\infty$이다.
증명
우선 $X$가 $C^\infty$라면 $X|_U$가 $C^\infty$인 것은 자명하다. 한편, $TM$에서 정의된 함수로서 $dx^i$들은 coordinate system $\tilde{\varphi}:\pi^{-1}(U)\rightarrow\mathbb{R}^{2m}$의 성분함수들이므로 마찬가지로 $C^\infty$이고, 따라서 이들의 합성
\[a^i(p)=dx^i\left(\sum a^i(p)\frac{\partial}{\partial x^i}\bigg|_p\right)=dx^i|_p\circ(X|_U)_p\]또한 $C^\infty$인 것이 자명하다.
2번 조건이 성립한다 가정하자. 임의의 $p\in V$에 대하여 $X(f)$가 $p$에서 $C^\infty$인 것을 보여야 하므로, 이를 위해서는 $p$를 포함하는 적당한 coordinate system $(U,\varphi)$에 대하여 $X(f)$가 $p$에서 $C^\infty$임을 보이면 충분하다. 이제 2번 조건에 의하여
\[(X|_U)_pf=\sum_{i=1}^m a^i(p)\frac{\partial f}{\partial x^i}(p)\]이고, 그럼 우변의 식은 $U$ 위에서 정의된 $C^\infty$ 함수가 되므로 $X(f)$가 $C^\infty$ 함수이다.
마지막으로 3번 조건을 가정하고 1번을 보이자. $X:M\rightarrow TM$이 $C^\infty$임을 보이기 위해서는 임의의 coordinate system $(U,\varphi)$에 대하여 $X\circ\varphi^{-1}$가 $\varphi(U)$에서 $TM$으로의 $C^\infty$ 함수임을 보이면 되고, 이는 다시 $TM$의 coordinate system을 생각하면 다음의 함수들
\[x^i\circ\pi\circ (X|_U),\quad dx^i\circ(X|_U)\]들이 $C^\infty$임을 보이면 된다. 그런데 직접 계산을 해 보면
\[x^i\circ\pi\circ (X|_U)=x^i\circ\id_U=x^i,\qquad dx^i\circ(X|_U)=X(x^i)\]가 성립하므로 이들은 모두 $C^\infty$가 된다.
$M$ 위에서 정의된 $C^\infty$-벡터장들의 모임을 $\mathfrak{X}(M)$으로 적으며, 앞으로 벡터장은 모두 $C^\infty$인 것으로 가정한다. 한편 partition of unity에 의하여, $M$의 어떠한 열린집합 $U$에서만 정의된 벡터장 또한 $M$ 전체로 확장할 수 있다. (§접공간, 각주 1)
Local frame
공간 $\mathfrak{X}(M)$의 두 원소 $X,Y$의 덧셈은 다음과 같이 잘 정의된다.
\[(X+Y)_p=X_p+Y_p\]또, 임의의 실수 $\alpha\in\mathbb{R}$에 대하여
\[(\alpha X)_p=\alpha\cdot X_p\]으로 정의하면 $\alpha X$ 또한 $\mathfrak{X}(M)$의 원소이므로, $\mathfrak{X}(M)$은 $\mathbb{R}$-벡터공간이 된다. 그러나 $\mathbb{R}$-벡터공간으로서 $\mathfrak{X}(M)$은 너무 거대하다.
예시 3 $M=\mathbb{R}$로 두자. 여기서 $M$은 하나의 chart $(\mathbb{R},\id)$을 통해 manifold 구조가 주어진 것으로 생각한다. 그럼 각 점 $p$에서 tangent space $T_pM$은 $d/dx\vert_p$을 통해 생성되는 1차원 벡터공간이며, 따라서 다음 대응
\[X:M\rightarrow TM;\qquad p\mapsto \frac{d}{dx}\bigg\vert_p\]은 $\mathfrak{X}(M)$의 원소이다. 그러나 임의의 $C^\infty$ 함수 $f:\mathbb{R}\rightarrow\mathbb{R}$에 대하여,
\[fX:M\rightarrow TM;\qquad p\mapsto f(p)\frac{d}{dx}\bigg\vert_p\]또한 $\mathfrak{X}(M)$에 속하며 (명제 2) 이 원소는 $f$가 상수함수가 아닌 이상 $fX$는 $X$의 상수배로 표현되지 않는다. 뿐만 아니라 $C^\infty(M)$은 $\mathbb{R}$ 위의 무한차원 벡터공간이므로 $\mathfrak{X}(M)$ 또한 무한차원 벡터공간이다.
위와 같은 상황에서 $\mathfrak{X}(M)$을 $C^\infty(M)$-module로 본다면 $\mathfrak{X}(M)$을 다루는 것이 상대적으로 편해진다.
위에서는 $\mathfrak{X}(M)$이 벡터장 $d/dx$로 생성되었지만, 일반적으로 $C^\infty(M)$은 field가 아니므로 basis를 갖지 않는 $C^\infty(M)$-module이 얼마든지 존재할 수 있다. 가령 잘 알려진 hairy ball theorem은 3차원 상에 있는 단위구 $S^2$ 상에 정의된 연속인 벡터장은 반드시 $0$이 되는 점이 존재한다는 것을 보여준다.
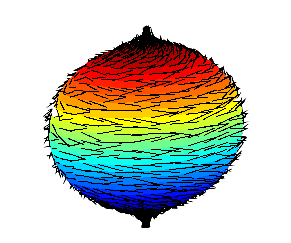
$2$-manifold $M=S^2$ 위에 정의된 두 vector field $X_1,X_2$가 $\mathfrak{X}(M)$을 $C^\infty(M)$-module로서 생성한다고 가정하자. 그럼 hairy ball theorem으로부터 $X_1(p)=0$인 점 $p\in S^2$가 존재한다. 그럼 $T_pM$은 $\{0,X_2(p)\}$로 생성되어야 하는데, 이는 $T_pM$이 2차원이라는 것에 모순이다. 따라서 $\mathfrak{X}(M)$을 두 벡터장 $\{X_1,X_2\}$으로 생성할 수는 없다.
반면 충분히 작은 열린집합 $U$에 대하여, $U$ 위에서 정의된 벡터장들의 모임 $\mathfrak{X}(U)$은 $m$개의 벡터장으로 생성되는 $C^\infty(U)$-module로 생각할 수 있다. Tangent bundle $\pi: TM\rightarrow M$에 대하여 열린집합 $U$를 충분히 작게 잡으면 diffeomorphism $h:U\times\mathbb{R}^m\rightarrow\pi^{-1}(U)$을 찾을 수 있으므로, 벡터장 $X_1,\ldots, X_m$을
\[X_1(p)=h(p, e_1),\quad X_2(p)=h(p,e_2),\quad\ldots,\quad X_m(p)=h(p,e_m)\tag{1}\]으로 정의하면 이들이 $\mathfrak{X}(U)$를 생성한다.
정의 4 Manifold $M$이 주어졌다 하고, $\dim M=m$이라 하자.
- $X_1,\ldots, X_k$가 $M$의 부분집합 $A$에서 일차독립linearly independent이라는 것은 각각의 $p\in A$마다 $T_pM$의 벡터들 $X_1(p),\ldots, X_k(p)$이 linearly independent인 것이다.
- $X_1,\ldots, X_k$가 $M$의 부분집합 $A$에서 tangent bundle $TM$을 생성span한다는 것은 각각의 $p\in A$마다 $T_pM$의 벡터들 $X_1(p),\ldots, X_k(p)$이 $T_pM$을 생성하는 것이다.
- 열린집합 $U\subseteq M$에서 정의된 일차독립인 벡터장들 $X_1,\ldots, X_k$이 tangent bundle을 생성한다면 이들을 $M$의 local frame이라 부른다.
- 위의 정의에서 만일 $U=M$이도록 잡을 수 있다면 이 벡터장들을 $M$의 global frame이라 부른다.
따라서, 위의 논의로부터 parallelizable manifold는 global frame을 갖는다는 것을 알 수 있다. 거꾸로 어떤 manifold $M$이 global frame $X_1,\ldots, X_m$을 갖는다면, 함수 $TM\rightarrow M\times\mathbb{R}^m$을
\[(p,a_1X_1(p)+\cdots+a_mX_m(p))\mapsto (p,a_1e_1+\cdots+a_me_m)\]으로 정의하여 $M$이 parallelizable manifold임을 확인할 수 있다.
Integral flow
정의 5 Manifold $M$의 $C^\infty$ curve $\sigma$가 $X\in\mathfrak{X}(M)$의 integral flow라는 것은 $\sigma’(t)=X(\sigma(t))$가 모든 $t$에 대해 성립하는 것이다.
다음 정리는 상미분방정식으로부터 쉽게 얻어지는데, 증명 자체는 우리의 관심사에서 벗어나므로 생략하기로 한다. 또, 정리의 4번 항목부터는 약간의 추가적인 정의가 필요하다.
정리 6 Manifold $M$과 $X\in\mathfrak{X}(M)$을 생각하자. 임의의 $p\in M$이 주어질 때마다, ($\pm\infty$를 포함하는) 적당한 상수 $a(p), b(p)$과 $C^\infty$ curve $\phi_p: \bigl(a(p),b(p)\bigr)\rightarrow M$이 존재하여 다음 조건들을 만족한다.
- $0\in \bigl(a(p),b(p)\bigr)$, $\phi_p(0)=p$.
- $\phi_p$는 $X$의 integral flow이다.
- 만일 $\mu:(c,d)\rightarrow M$이 위의 두 조건을 만족하는 $C^\infty$ 함수라면 $(c,d)\subseteq \bigl(a(p),b(p)\bigr)$이고, $\mu$는 $\phi_p$를 $(c,d)$로 제한한 것과 동일한 함수이다.
- 각각의 $p\in M$마다 적당한 열린근방 $V$와 양수 $\epsilon$이 존재하여, $(t,p)\mapsto \phi^{t}(p):=\phi_p(t)$가 잘 정의되며, 이 함수는 $(-\epsilon,\epsilon)\times V$에서 $M$으로의 $C^\infty$ 함수이다.
- 임의의 $t$에 대해 $\mathcal{D}_t=\left\{p\in M\mid t\in\bigl(a(p),b(p)\bigr)\right\}$가 열린집합이다.
- $\bigcup_{t>0}\mathcal{D}_t=M$.
- $\phi^{t}:\mathcal{D}_t\rightarrow\mathcal{D}_{-t}$는 diffeomorphism이고, 그 역함수는 $\phi^{-t}$이다.
- $\phi^s\circ \phi^t$의 정의역은 $\mathcal{D}_{s+t}$에 포함되며, 특히 $s$와 $t$가 같은 부호일 경우 이 함수의 정의역은 정확히 $\mathcal{D}_{s+t}$와 동일하다. 또, 이 정의역 상에서 $\phi^s\circ \phi^t=\phi^{t+s}$이다.
증명은 생략하더라도, 이 정리가 뜻하는 바는 완벽하게 이해할 필요가 있다.
우선 위 정리의 1번부터 3번까지의 내용은 임의의 $p\in M$마다 maximal integral flow가 하나씩 대응되며, 이는 시간 $t$의 설정을 제외하면 유일하게 결정된다는 것을 보여준다.
정리의 나머지 부분을 이해하기 위해서는 표기법에 대한 추가적인 설명이 필요하다. 우선 4번 조건의 함수 $\phi^{t}(p)$는 정의와 같이
\[\phi^{t}(p)=\phi_p(t)\]정의되는 함수이며, 여기에서 초기값은 시간이 $0$일 때 $\phi_p(0)=p$으로 고정한다는 의미이다. 이 때, $\phi^{t}$의 정의역을
\[\mathcal{D}_t=\left\{p\in M\mid t\in\bigl(a(p),b(p)\bigr)\right\}\]로 나타낸다. 즉 $\phi^{t}$은 시간 $0$에서 점 $p$에 있던 점이 integral flow를 따라 움직일 경우 $t$초 후에 있을 위치를 나타내는 함수로 생각할 수 있고, $\mathcal{D}_t$는 이렇게 integral flow를 따라 $t$초만큼 움직이는 것이 가능한 점들의 모임이다.
이제 기술적인 결과인 4번과 5번을 제외하면 그 다음으로 나오는 결과는 6번의 결과인데, 이는 사실 integral flow의 존재성을 다른 방식으로 서술한 것에 불과하다. 7번의 결과는 integral flow들이 서로 섞이지 않는다는 것을 보여준다.
8번의 결과 또한 약간 기술적인 측면이 있는데, 만일 $s$와 $t$가 다른 부호였다면, 가령 $s=-2$이고 $t=1$이었다면 $\phi^s\circ\phi^t$의 정의역은 단순히 $\mathcal{D}_{-1}$가 아니라, $\mathcal{D}_{-1}$의 원소들 중 $\phi_p$를 따라 1초만큼 진행하는 것도 가능한 점들만으로 이루어진 집합이다.
정의 7 $X\in\mathfrak{X}(M)$이 complete라는 것은 모든 $t$에 대하여 $\mathcal{D}_t=M$이라는 것이다. 이 때, $\phi^t$들은 $\circ$에 대한 group을 이루는데, 이를 $X$의 one-parameter group이라 부른다.
만일 $X$가 complete이 아니라면 위와 같이 $\phi^t$들의 정의역에 약간의 문제가 있어 이들을 group으로 생각하기가 힘들어진다. 더 미묘한 경우는 처음의 벡터장 $X$가 시간에 따라 변하는 경우인데, 이 경우는 아직은 우리의 관심사가 아니니 넘기기로 한다.
참고문헌
[War] Frank W. Warner. Foundations of Differentiable Manifolds and Lie Groups, Graduate texts in mathematics, Springer, 2013
[Lee] John M. Lee. Introduction to Smooth Manifolds, Graduate texts in mathematics, Springer, 2012

댓글남기기