우리는 이전 글에서 $\mathbb{R}$에 manifold 구조를 주는 서로 다른 두 가지 방법을 살펴봤다. 이 글에서는 더 일반적인 위상공간에 manifold 구조가 주어진 다양한 예시들을 살펴본다.
Manifold는 국소적으로 $\mathbb{R}^m$과 닮은 구조이므로, 가장 간단한 예시는 당연히 $\mathbb{R}^m$ 그 자체다.
예시 1 Standard topology가 주어진 $\mathbb{R}^m$ 위에 정의된 standard differentiable structure는 atlas $\{(\mathbb{R}^m,\id_{\mathbb{R}^m})\}$으로 주어진다.
앞선 글에서의 예시와 마찬가지로, $\mathbb{R}^m$에서도 서로 다른 미분구조를 주는 것이 가능하다.
예시 2 조금 더 일반적으로, $m$차원 $\mathbb{R}$-vector space $V$가 주어졌다 하자. $V$의 basis $\mathcal{B}$를 고르고, $\mathcal{B}$에 대한 coordinate representation $\varphi_\mathcal{B}:v\mapsto [v]_{\mathcal{B}}$를 생각하자. 이 선형사상은 isomorphism이므로, bijection이고 따라서 이를 통해 $\mathbb{R}^m$의 위상과 미분구조를 모두 $V$로 옮겨올 수 있다. $\varphi_\mathcal{B}$를 통해 $\mathbb{R}^m$의 미분구조를 옮겨온다는 것은 $(V,\mathcal{B})$에 하나의 coordinate system $(V,\varphi_{\mathcal{B}})$를 통해 미분구조를 정의하는 것과도 같다.
물론 이 함수들 자체는 기저의 선택에 의존하지만, 이렇게 정의된 위상구조와 미분구조는 기저의 선택에 무관하다.
우선 이러한 방식으로 정의된 $V$ 위에서의 norm은 기저의 선택과 무관하게 equivalent한 거리구조를 주므로, 서로 다른 기저 $\mathcal{B}$와 $\mathcal{C}$가 주어진 벡터공간 $(V,\mathcal{B})$와 $(V,\mathcal{C})$는 동일한 위상구조를 갖는다. 한편, 이들은 동일한 미분구조를 갖기도 한다. 이를 위해서는 $(V,\varphi_\mathcal{B})$와 $(V,\varphi_\mathcal{C})$에 대해 transition map $\varphi_\mathcal{B}\circ\varphi_\mathcal{C}^{-1}$와 $\varphi_\mathcal{C}\circ\varphi_\mathcal{B}^{-1}$가 모두 $C^\infty$라는 것을 보이면 되는데, 이들은 사실 행렬들이고, 따라서 다항식이므로 당연히 $C^\infty$이다.
이에 대한 특수한 경우로,
- $n\times n$ 행렬들의 집합 $\Mat_n(\mathbb{R})$은 $n^2$차원 벡터공간이므로 미분구조를 갖는다.
- $\mathbb{C}^n$의 경우, $2n$차원 $\mathbb{R}$-벡터공간으로 생각할 수 있으므로 역시 미분구조를 갖는다.
추가적인 예시를 위해서는 우선 다음을 정의해야 한다.
정의 3 Manifold $M$이 주어졌다 하자. $M$의 열린집합 $V$에 다음의 두 구조
- $M$의 위상으로부터 주어지는 subspace topology,
-
$M$에 정의된 미분구조 $\mathcal{A}$에 대하여,
\[\mathcal{A}_V=\{(U_\alpha\cap V,\varphi_\alpha|_{U_\alpha\cap V})\mid(U_\alpha,\varphi_\alpha)\in\mathcal{A}\}\]
를 주면, $V$는 $M$과 동일한 차원의 manifold가 된다. 이러한 manifold 구조를 $M$의 open submanifold라 부른다.
물론 이 정의가 잘 정의되기 위해서는 subspace topology가 locally Euclidean, second countable, Hausdorff 조건을 모두 만족해야 하고, $\mathcal{A}_V$의 원소들이 각각 $C^\infty$-compatible해야 한다. 하지만 Hausdorff, second countability는 모두 subspace topology에 의해 잘 보존되는 성질이며, locally Euclidean 성질 또한 $V$가 열린집합이라는 사실로부터 얻어낼 수 있다. 뿐만 아니라, $\mathcal{A}_V$의 원소들 사이의 transition map은 $C^\infty$ 함수들의 restriction들이므로 이들 또한 $C^\infty$이다.
예시 4 $\Mat_{n}(\mathbb{R})$의 원소들 중, 역행렬을 갖는 $n\times n$ 행렬들의 집합 $\GL(n,\mathbb{R})$은 $\det(A)\neq 0$을 만족하는 행렬들의 모임이다. 행렬식 $\det$를 $\Mat_n(\mathbb{R})$에서 $\mathbb{R}$로의 함수로 보면, 이 함수는 다항함수이므로 연속이고, 따라서 열린집합 $\mathbb{R}\setminus\{0\}$의 preimage인 $\GL(n,\mathbb{R})$ 또한 $\Mat_n(\mathbb{R})$의 열린집합이다. 따라서 $\GL(n,\mathbb{R})$은 $n^2$차원 manifold이다.
한편, $\GL(n,\mathbb{R})$은 $\det A>0$인 행렬들과 $\det A<0$인 행렬들의 disjoint union이며, 이들 집합 각각은 위와 마찬가지 이유로 열린집합이므로 $\GL(n,\mathbb{R})$은 connected는 아니다.
예시 5 열린집합 $U\subset\mathbb{R}^m$과 $C^\infty$ 함수 $f:U\rightarrow\mathbb{R}^n$에 대하여 $f$의 그래프 $\graph(f)$를 다음의 집합
\[\graph(f)=\{(x,y)\in\mathbb{R}^m\times\mathbb{R}^n\mid \text{$x\in U$, $y=f(x)$}\}\]으로 정의하자. 그럼 $f:U\rightarrow\graph(f)$와, 앞의 $m$개의 좌표로의 projection $\pr:\graph(f)\rightarrow U$가 모두 연속이고, 서로의 역함수가 되므로 $\graph(f)$와 $U$는 homeomorphic이다. 따라서 $\graph(f)$는 topological manifold이며, 특히 projection $\pr:\graph(f)\rightarrow U$이 하나의 chart로 이루어진 atlas $\{(\graph(f),\pr)\}$를 이루므로 자연스러운 (differentiable) manifold 구조 또한 갖는다.
지금까지의 예시에서는 모두 하나의 chart만을 갖는 atlas를 통해 미분구조를 주었는데, 이는 곧 manifold가 국소적으로 $\mathbb{R}^m$과 닮아있을 뿐만 아니라, 전체적으로도 $\mathbb{R}^m$과 닮아있다는 뜻이므로 사실 그렇게 흥미로운 상황이 아니다.
예시 6 $\mathbb{R}^{n+1}$에 들어있는 $n$차원 구면 $S^n$을 생각하자. $S^n$에 subspace topology를 주면 Hausdorff, second coutability 조건이 모두 만족된다. 하지만 $S^n$은 열린집합이 아니므로, locally Euclidean 조건을 보이는 것이 open submanifold의 경우보다 더 까다롭다.
임의의 $p\in S^n$을 고르자. $0\not\in S^n$이므로, $p$의 어떤 좌표는 반드시 0이 아니다. 일반성을 잃지 않고, 이 좌표가 $n+1$ 번째 좌표라 하고, 또 양수라 하자. 즉 $p$는 다음의 집합
\[U_{n+1}^+=\{(x^1, x^2, \ldots, x^{n+1})\in\mathbb{R}^{n+1}\mid x^{n+1}>0\}\]의 원소이다.
그림으로 보면 거의 자명하게 $U_{n+1}^+$와 $D^n$이 homeomorphic하다는 것을 알 수 있다.
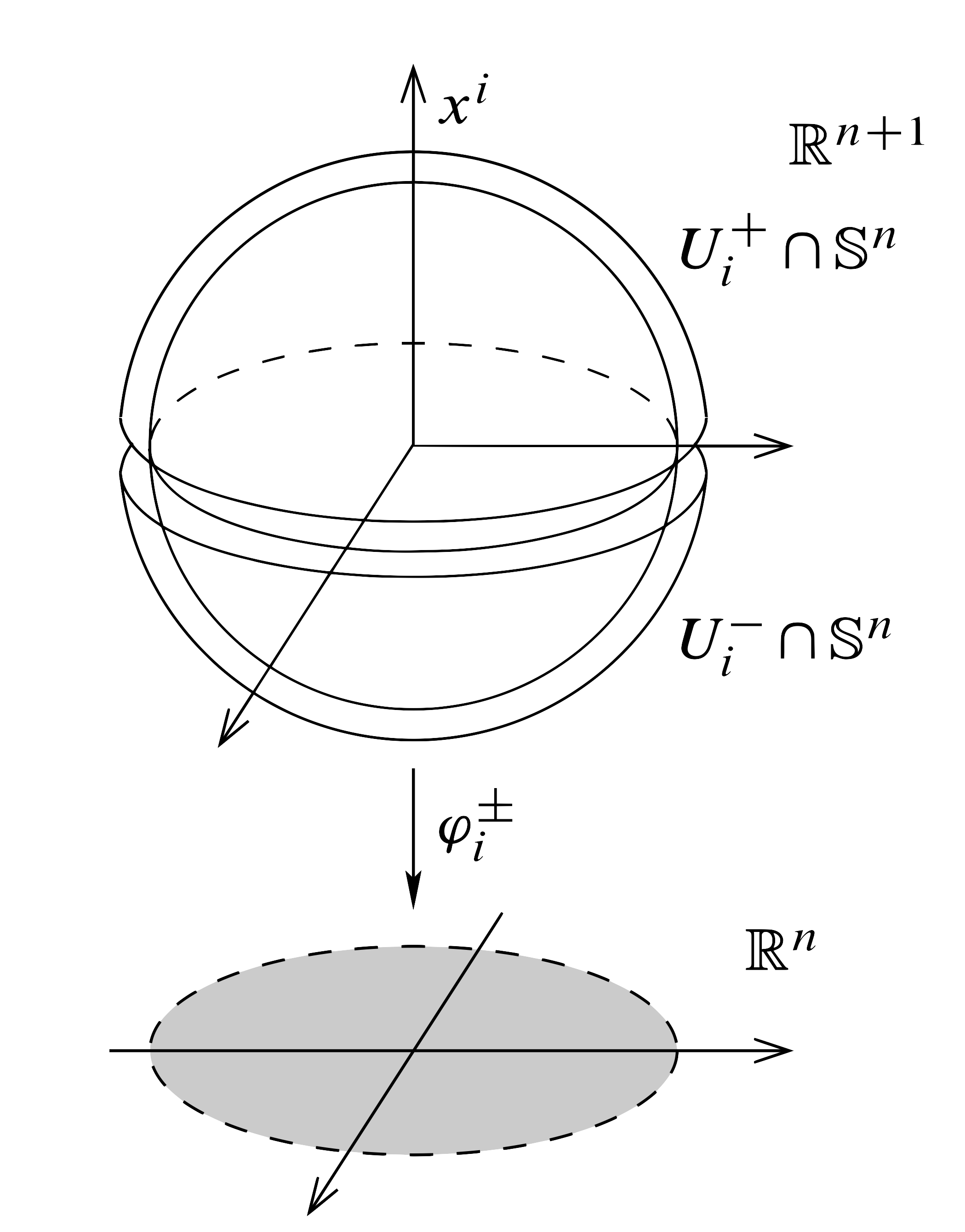
이를 수식으로 엄밀하게 적기 위해, $D^n$의 한 점 $x=(x^1,\ldots, x^n)$마다 함수 $f:D^n\rightarrow\mathbb{R}$을 다음의 식
\[f(x)=\sqrt{1-\lvert x\rvert^2}\]으로 정의하자. 그럼 $f$는 $D^n$에서 $C^\infty$이고, 더 나아가 $D^n$과 $\graph(f)=U_{n+1}^+$사이의 homeomorphism을 정의한다. 따라서 locally Euclidean 조건이 성립한다.
뿐만 아니라 이들 $U_i^\pm$들과, $i$번째 좌표를 제외한 $n$개의 좌표로의 projection $\varphi_i^\pm$들을 모은 다음의 집합
\[\mathcal{A}=\{(U_i^\pm, \varphi_i^\pm\mid i=1,2,\ldots, n+1\}\]이 atlas가 된다. 이를 위해서는 위 atlas를 구성하는 chart들이 모두 $C^\infty$-compatible이라는 것을 보여야 한다. $U_i^+$와 $U_i^-$는 만나지 않으므로 자명하게 서로 $C^\infty$-compatible하다. 서로 다른 index $i,j$를 갖는 두 chart $(U_i^\pm, \varphi_i^\pm)$와 $(U_j^\pm,\varphi_j^\pm)$가 주어졌다 하자. 그럼 우선 $(\varphi_i^\pm)^{-1}$에 의하여
\[(x^1, x^2, \ldots, x^n)\mapsto (x^1, x^2, \ldots, x^{i-1}, \pm \sqrt{1-\lvert x\rvert^2}, x^i, \ldots, x^n)\]이고, 이후 $\varphi_j^\pm$에 의하여
\[(x^1, x^2, \ldots, x^{i-1}, \pm \sqrt{1-\lvert x\rvert^2}, x^i, \ldots, x^n)\mapsto (x^1, x^2, \ldots, \hat{x}^j, \ldots, x^{i-1}, \pm \sqrt{1-\lvert x\rvert^2}, x^i, \ldots, x^n)\]이다. 여기서 $\hat{x}^j$는 $j$번째 성분이 없다는 것을 의미한다. 이 때, 우변의 식의 각 성분이 $x^i$들에 대한 $C^\infty$함수들이므로 $(\varphi_j^{\pm})\circ(\varphi_i^\pm)^{-1}$은 $C^\infty$이고, 비슷하게 $(\varphi_i^{\pm})\circ(\varphi_j^\pm)^{-1}$ 또한 $C^\infty$임을 확인할 수 있다. 따라서 위의 집합 $\mathcal{A}$는 $S^n$ 위에 미분구조를 정의한다.
$S^n$ 위에 정의된 미분구조는 manifold의 전형적인 예시이다. 다음 예시는 위의 예시와는 다른 방법으로 $S^n$에 (동일한) 미분구조를 부여하는데, differential을 정의하고, 이 예시를 더욱 일반화하여 manifold 구조를 줄 수 있다.
예시 7 $\mathbb{R}^n$의 부분집합 $U$와, $U$ 위에서 정의된 $C^\infty$ 함수 $F$가 주어졌다 하자. 그럼 level set $M=F^{-1}(c)$가 잘 정의된다. 만일 여기에 더하여, 다음의 Jacobian matrix
\[\begin{pmatrix}\frac{\partial F^1}{\partial x^1}&\frac{\partial F^1}{\partial x^2}&\cdots&\frac{\partial F^1}{\partial x^n}\\\frac{\partial F^2}{\partial x^1}&\frac{\partial F^2}{\partial x^2}&\cdots&\frac{\partial F^2}{\partial x^n}\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial F^n}{\partial x^1}&\frac{\partial F^n}{\partial x^2}&\cdots&\frac{\partial F^n}{\partial x^n}\end{pmatrix}\]가 항상 0이 아니라 하자. 즉, 각 점 $a\in M$마다 어떠한 $i$가 존재하여, 열벡터 $dF/dx^i$가 영벡터가 아니도록 할 수 있다. 그럼 음함수 정리에 의하여, 점 $a$의 적당한 열린근방 $U$에서는 $M$이
\[x^i=f(x^1,\ldots, \hat{x}^i,\ldots, x^n)\]의 그래프이도록 하는 함수 $f$가 존재한다.
이제 예시 6과 마찬가지로, $M$에 subspace topology를 주고, 방금 만든 $(U, f)$들을 이용해 chart를 만들면 $M$이 $(n-1)$차원 manifold가 된다는 것을 확인할 수 있다.
예시 7을 이용하여 $S^n$을 $\mathbb{R}^{n+1}$ 위에서 정의된 함수
\[F(x^1,\ldots, x^{n+1})=(x^1)^2+(x^2)^2+\cdots+(x^{n+1})^2-1\]의 zero set으로 볼 수 있으므로 예시 6은 위 예시의 특별한 경우로 볼 수 있다.
예시 8 집합 $\mathbb{R}^{n+1}\setminus\{0\}$에 $x\sim y\iff \exists\lambda(x=\lambda y)$으로 정의된 relation이 주어졌다 하자. 어렵지 않게 $\sim$이 equivalence relation임을 확인할 수 있다. 이제 quotient set $\RP^n=\RP^n/\sim$을 canonical projection $\pi:\mathbb{R}^{n+1}\setminus\{0\}\rightarrow \RP^n$을 통해 정의된 quotient topology로 생각하고, $[x]$가 $x\in\mathbb{R}^{n+1}\setminus\{0\}$의 representative라 하자.
각각의 $i=1,\ldots, n+1$에 대하여, $\mathbb{R}^{n+1}\setminus\{0\}$의 열린집합
\[\tilde{U}_i=\{(x^1,\ldots, x^{n+1})\mid x^i\neq 0\}\]을 생각하자. 그럼 $\tilde{U}_i$는 saturated인 열린집합이므로, [위상수학] §몫공간, ⁋명제 8에 의하여 quotient map $\pi$가 $\tilde{U}_i$로 잘 제한된다. 따라서, 함수 $\varphi_i:U_i\rightarrow\mathbb{R}^n$을
\[\varphi_i[x^1,\ldots, x^{n+1}]=\left(\frac{x^1}{x^i},\ldots,\frac{x^{i-1}}{x^i},\frac{x^{i+1}}{x^i},\ldots, \frac{x^{n+1}}{x^i}\right)\]으로 정의하면1 함수 $\varphi_i\circ\pi|_{\tilde{U}_i}$가 연속이고 따라서 [위상수학] §몫공간, ⁋명제 9에 의해 $\varphi_i$ 또한 연속이다.
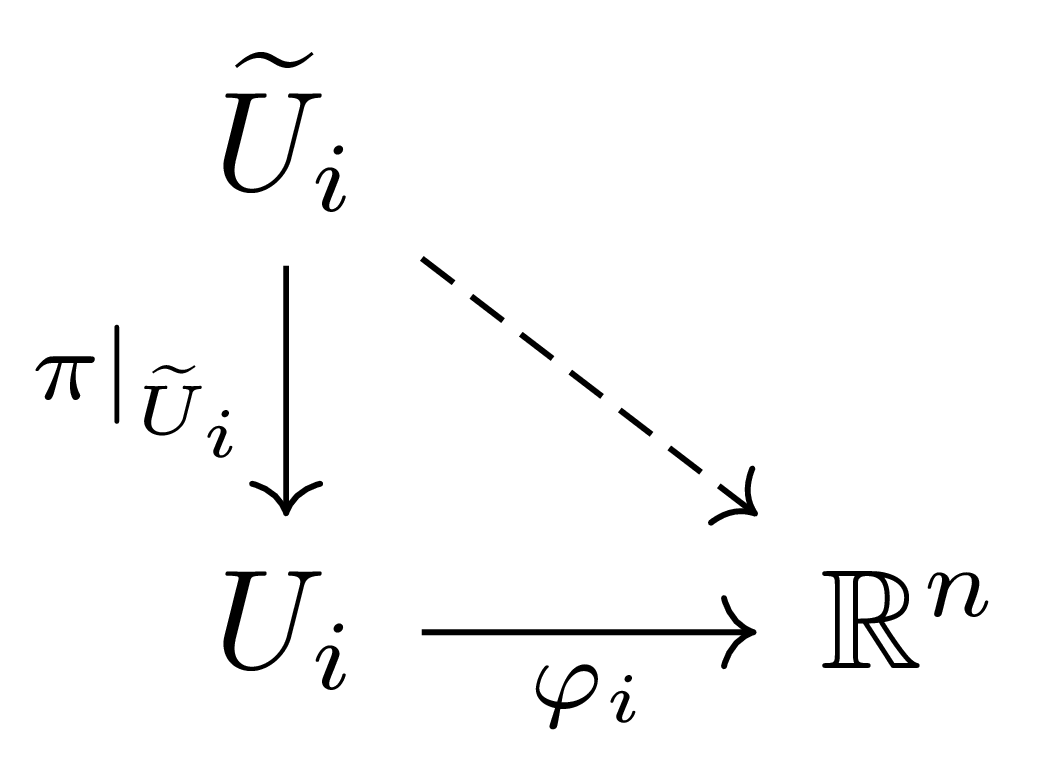
뿐만 아니라 다음의 연속함수
\[\psi_i:(u^1, \ldots, u^n)\mapsto [u^1, \ldots, u^{i-1}, 1, u^i,\ldots, u^n]\]이 $\varphi_i$의 역함수임을 쉽게 확인할 수 있으므로, 이들 $U_i$들은 모두 $\mathbb{R}^n$과 homeomorphic하다. 즉, $\RP^n$은 $n$차원 locally Euclidean이다. Quotient topology의 성질로부터 $\RP^n$이 Hausdorff이고 second countable임을 알 수 있으므로, $\RP^n$은 topological manifold가 된다.
한편, 이들 $(U_i,\varphi_i),(U_j,\varphi_j)$들 간의 transition map을 생각해보면, 우선 $\varphi_j^{-1}$에 의하여
\[(u^1, \ldots, u^n)\mapsto [u^1, \ldots, u^{j-1}, 1, u^j,\ldots, u^n]\]이고, 이후 $\varphi_i$를 타고 가면
\[[u^1, \ldots, u^{j-1}, 1, u^j,\ldots, u^n]\mapsto \left(\frac{u^1}{u^i},\ldots,\frac{u^{j-1}}{u^i}, \frac{1}{u^i}, \frac{u^j}{u^i},\ldots, \frac{u^{i-1}}{u^i},\frac{u^{i+1}}{u^i},\ldots, \frac{u^{n+1}}{u^i}\right)\]이므로 $C^\infty$-compatible하다.
마지막으로 약간 일반적인 예시를 살펴보자.
예시 9 각각 $m,n$차원의 manifold $(M,\mathcal{A}_M),(N,\mathcal{A}_N)$들이 주어졌다 하자. 그럼 이들의 product manifold는 $M\times N$에 product topology를 준 후, differentiable structure는
\[\mathcal{A}=\{(U_\alpha\times V_\beta,\varphi_\alpha\times\psi_\beta)\mid (U_\alpha,\varphi_\alpha)\in\mathcal{A}_M,(V_\beta,\psi_\beta)\in\mathcal{A}_N\}\]을 통해 정의되는 manifold이다.
참고문헌
[Lee] John M. Lee. Introduction to Smooth Manifolds, Graduate texts in mathematics, Springer, 2012
[War] Frank W. Warner. Foundations of Differentiable Manifolds and Lie Groups, Graduate texts in mathematics, Springer, 2013
-
사실은 이 함수는 $\RP^n$의 부분집합에서 $\mathbb{R}^n$으로의 함수이므로, 우변의 결과가 representative의 선택에 의존하지 않는 것을 보여야 한다. 즉 만일 $[\lambda x^1,\ldots, \lambda x^{n+1}]$을 representative로 택했어도 같은 결과가 나와야 하는데, 이는 식으로부터 명확하다. ↩

댓글남기기