리 군과 리 대수 사이에는 긴밀한 관계가 있다. 자세한 증명은 리 군을 다루는 별도의 카테고리로 미뤄두고, 이번 글에서는 앞으로 주로 쓰이게 될 관계들을 결과들 위주로 살펴본다. 그 후, 이를 활용하여 Lie group 위에서의 exponential map을 정의한다.
Homomorphism
Lie group과 Lie algebra의 homomorphism은 언제나와 같이 이들의 구조를 보존하는 함수를 뜻한다.
정의 1 임의의 두 Lie group $G,H$에 대하여, $F:G\rightarrow H$가 Lie group homorphism리 군 준동형사상인 것은 $F$가 $C^\infty$인 동시에 group homomorphism인 것이다. 만일 여기에 더해, $F$가 diffeomorphism이라면 이를 Lie group isomorphism리 군 동형사상이라 부른다.
임의의 두 Lie algebra $\mathfrak{g},\mathfrak{h}$에 대하여, $L:\mathfrak{g}\rightarrow \mathfrak{h}$가 Lie algebra homomorphism리 대수 준동형사상인 것은 $L$이 linear map인 동시에 Lie bracket을 보존하는 것이다. 만일 여기에 더해, $L$이 전단사함수라면 이를 Lie algebra isomorphism리 대수 동형사상이라 부른다.
편의를 위해, 앞으로는 Lie group 혹은 Lie algebra들 사이의 homomorphism, isomorphism 등등은 모두 Lie group (algebra) homomorphism, Lie group (algebra) isomorphism 등등을 지칭하는 것으로 한다.
임의의 Lie group homomorphism $F:G \rightarrow H$가 주어졌다 하자. 그럼
\[(dF)_e:T_eG\rightarrow T_{F(e)}H=T_e H\]와 §리 군, ⁋명제 6으로부터, $dF$가 $\mathfrak{g}$에서 $\mathfrak{h}$로의 homomorphism을 유도한다는 것을 쉽게 증명할 수 있다.
명제 2 Lie group homomorphism $F:G \rightarrow H$가 주어졌다 하자.
- 임의의 $X\in \mathfrak{g}$에 대하여, $dF(X)$와 $X$는 $F$-related이다.
- $dF:\mathfrak{g} \rightarrow \mathfrak{h}$는 homomorphism이다.
거꾸로, Lie algebra homomorphism $\mathfrak{g}\rightarrow \mathfrak{h}$이 주어졌을 때 그에 해당하는 Lie group들 $G,H$ 사이의 homomorphism $G\rightarrow H$를 복원할 수 있다는 것이 잘 알려져 있다.
정리 3 Lie group $G,H$가 주어졌다 하고, 이들의 Lie algebra $\mathfrak{g},\mathfrak{h}$ 사이의 homomorphism $L:\mathfrak{g} \rightarrow \mathfrak{h}$이 주어졌다 하자. 만일 $G$가 simply connected라면, $dF=L$을 만족하는 homomorphism $F:G \rightarrow H$가 유일하게 존재한다.
Lie subgroup
정의 4 Lie group $G$에 대하여, submanifold $\Phi:H\hookrightarrow G$가 Lie subgroup리 부분군이라는 것은 $H$가 Lie group이며 $\iota$가 group homomorphism인 것이다.
Lie subgroup을 다룰 때 중요하게 사용할 수 있는 정리는 다음의 closed subgroup theorem이다.
정리 5 (Closed subgroup theorem) Lie group $G$와 Lie subgroup $\Phi:H\rightarrow G$가 주어졌다 하자. 그럼 $H$가 $G$의 embedded submanifold인 것과 $\Phi(H)$가 $G$에서 닫힌집합인 것이 동치이다.
다음 정리는 정리 3과 마찬가지로, Lie group의 Lie subgroup들과 Lie algebra의 subalgebra들 사이에 일대일대응이 존재한다는 것을 보여준다.
정리 6 Lie group $G$가 주어졌다 하고, $\mathfrak{g}$의 subalgebra $\tilde{\mathfrak{h}}$가 주어졌다 하자. 그럼 유일한 connected Lie subgroup $\Phi:H \rightarrow G$가 존재하여 $dF(\mathfrak{h})=\tilde{\mathfrak{h}}$이도록 할 수 있다.
Covering space
정리 3에서 $G$가 simply connected라는 조건이 필요한 것은 이를 증명하기 위해 Lie group $G$의 (universal) covering space를 생각할 필요가 있기 때문이다. 우리는 해당 정리의 결과만 소개하였으므로 이들을 사용할 일은 없었으나, 그 결과는 흥미로우므로 소개해둔다.
명제 7 두 connected Lie group $G,H$과 homomorphism $F:G\rightarrow H$를 생각하자. 그럼 $F$가 covering map인 것과 $dF:G_e \rightarrow H_e$가 isomorphism인 것이 동치이다.
정리 8 임의의 connected Lie group $G$는 스스로 Lie group이 되는 동시에 covering map $p$가 Lie group homomorphism인 universal covering $p:\tilde{G}\rightarrow G$를 갖는다.
Exponential map
$(\mathbb{R},+)$은 Lie group이므로, 임의의 Lie group $G$에 대하여 curve $\gamma:\mathbb{R}\rightarrow G$는 Lie group 사이의 $C^\infty$ 함수이다.
정의 9 만일 $\gamma:\mathbb{R}\rightarrow G$가 Lie group들 사이의 homomorphism이기도 하다면, $\gamma$를 1-parameter subgroup이라 부른다.
즉 임의의 $s,t\in \mathbb{R}$에 대하여
\[\gamma(s+t)=\gamma(s)\gamma(t)\]가 성립한다.
명제 10 Lie group $G$가 임의로 주어졌다 하자. 그럼 임의의 $X\in\mathfrak{g}$에 대하여,
\[(d\gamma_X)\left(r\frac{d}{dt}\right)=rX\]을 만족하는 1-parameter subgroup $\gamma_X:\mathbb{R}\rightarrow G$가 유일하게 존재한다. (참고: §미분사상의 예시들, ⁋명제 2)
증명
$\mathbb{R}$과 $G$의 Lie algebra를 각각 $T_0 \mathbb{R}$, $T_eG$와 동일하게 취급하자. 우선 $T_0\mathbb{R}$은 1차원 $\mathbb{R}$-algebra이므로, $T_0 \mathbb{R}$에서 다른 $\mathbb{R}$-algebra로의 algebra homomorphism은 그 basis $d/dt$의 값으로 유일하게 결정된다. 따라서 다음의 식
\[\frac{d}{dt}\bigg|_{t=0}\mapsto X_e\in T_eG\]으로 정의된 Lie algebra들 사이의 homomorphism이 유일하게 존재한다. 이제 $\mathbb{R}$은 simply connected이므로, 정리 3으로부터 원하는 $\gamma_X$를 얻는다.
함수 $X\mapsto\gamma_X$는 $\mathfrak{g}$의 임의의 원소마다 곡선 $\gamma_X$를 하나씩 대응시킨다. 이렇게 얻어진 곡선 $\gamma_X$의 시간 $t=1$에서의 점은 $G$의 원소가 되며, 이를 통해 exponential map $\exp:\mathfrak{g}\rightarrow G$를 다음의 식
\[X\mapsto\gamma_X(1)\]으로 정의한다.
명제 11 Lie group $G$와 $X\in \mathfrak{g}$에 대하여 다음이 성립한다.
- $\exp(tX)=\gamma_X(t)$
- $\exp(t_1+t_2)X=(\exp t_1X)(\exp t_2X)$
- $\exp(-tX)=(\exp tX)^{-1}$
-
임의의 $g\in G$에 대하여, $L_g\circ\gamma_X$는 두 식
\[\gamma(0)=g,\qquad\gamma'(0)=X_g\]을 만족하는 유일한 integral curve이다.
증명
우선 명제 2로부터, $\mathbb{R}$ 위에 정의된 벡터장 $d/dt$와 $G$ 위에 정의된 벡터장
\[(d\gamma_X)\left(\frac{d}{dt}\right)\]이 $\gamma_X$-related이다. 그런데 위의 벡터장은 정확히 $X$와 같으므로,
\[\frac{d}{dt}\bigg|_t\gamma_X(t)=(d\gamma_X)_t\left(\frac{d}{dt}\bigg|_{t}\right)=X_{\small\gamma_{\tiny X}(t)}\]이다. 즉 $\gamma_X$는 $X$의 integral curve이며, 이는 초기조건 $\gamma_X(0)=e$를 통해 유일하게 결정된다. 이제 $X$가 left invariant이므로
\[d(L_g\circ\gamma_X)\left(\frac{d}{dt}\right)=d(L_g)\circ X=X\circ L_g\]로부터, 초기조건 $\gamma_X(0)=g$를 만족하는 $X$의 유일한 integral curve는 $L_g\circ\gamma_X$임을 알 수 있다.
이제 첫째 주장의 경우에는, 두 곡선 $t\mapsto\gamma_{sX}(t)$와 $t\mapsto\gamma_X(st)$가 모두 벡터장 $sX$의 integral curve를 정의한다는 것을 확인한 후, 따라서 $t=1$을 대입하여
\[\exp(sX)=\gamma_X(s)\]를 얻으면 된다. 둘째 주장과 셋째 주장은 $\exp$가 $\mathbb{R}$에서 $G$로의 homomorphism이므로 자명하다.
예시 12 임의의 행렬 $X\in\Mat_n(\mathbb{R})$에 대하여, 함수 $\exp_X$가
\[t\mapsto \exp_X(t):=\exp(tX)=I+tX+\frac{(tX)^2}{2!}+\cdots\]로 주어졌다 하자. 어렵지 않게 다음의 식
\[\exp_X(s+t)=\exp_X(s)\exp_X(t)\]이 성립하는 것을 알 수 있으므로, $\exp_X$의 치역은 $\GL(n,\mathbb{R})$에 속하고 따라서 $\exp_X$는 $\mathbb{R}$에서 $\GL(n,\mathbb{R})$로의 1-parameter subgroup이 된다. 한편 원점에서 이 함수의 differential을 계산해보면
\[(d\exp_X)_{t=0}\left(\frac{d}{dt}\bigg|_{t=0}\right)=\frac{d}{dt}\bigg|_{t=0}\exp(tX)=\exp(0X)X=X\]이므로 유일성에 의해 $\exp_X$는 명제 10을 Lie group $\GL(n,\mathbb{R})$에 적용하여 얻어지는 1-parameter subgroup과 같다.
위의 예시에서 $\exp_X(1)=\exp(X)$이므로, 일반적인 Lie group에 대하여 $X\mapsto\gamma_X(1)$을 exponential map이라 부르는 것이 자연스럽다.
§고전군에서 살펴본 예시들을 보면, Lie group을 정의하는 식에
정리 13 임의의 Lie group homomorphism $F:G\rightarrow H$에 대하여, 다음의 diagram
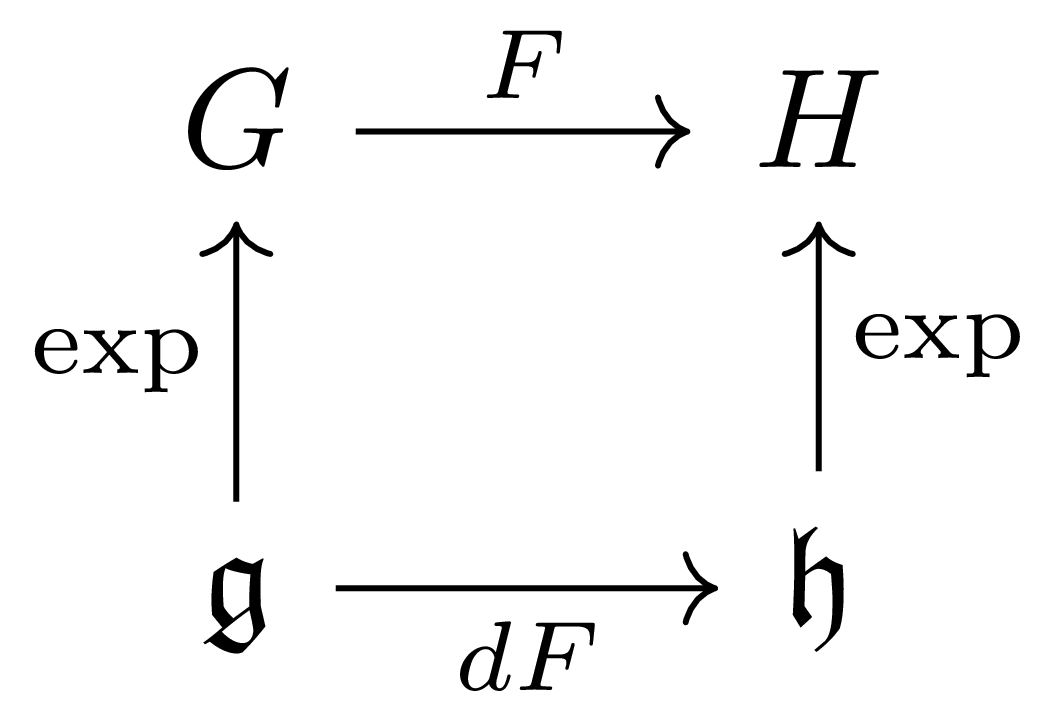
이 commute한다.
증명
임의의 $X\in\mathfrak{g}$에 대하여, $t\mapsto F(\exp tX)$는 $t=0$에서 $F(0)$을 지나고 그 때의 tangent vector가 $dF(X_e)$이다. 이제 주어진 diagram이 commute하는 것은 명제 10에서의 유일성에 의해 자명하다.
참고문헌
[War] Frank W. Warner. Foundations of Differentiable Manifolds and Lie Groups, Graduate texts in mathematics, Springer, 2013

댓글남기기