부분다양체의 정의
정의 1 두 manifold $M,N$과 $C^\infty$ 함수 $F:N\rightarrow M$이 주어졌다 하자.
- $F$가 immersion몰입이라는 것은 모든 $p\in N$에 대하여 $dF_p$가 단사인 것이고, 비슷하게 $F$가 submersion침몰이라는 것은 모든 $p\in N$에 대하여 $dF_p$가 전사인 것이다.
- 만일 $F$가 immersion인 동시에 단사함수이기도 하다면, $F$를 $M$의 submanifold부분다양체라 한다.
- 만일 $F$가 $M$의 submanifold일 뿐만 아니라, subspace topology가 주어진 $F(N)\subseteq M$과 $N$ 사이의 homeomorphism을 정의하기도 하다면 $F$를 embedding매장, 혹은 2번의 정의와 맞추어 embedded submanifold라 부른다.
3번의 embedded submanifold와 더 명확하게 구별하기 위해 2번을 immersed submanifold라 부르기도 한다. 우리는 위의 정의 그대로, 수식어 없는 submanifold를 immersed manifold의 뜻으로 사용하고, embedded submanifold는 축약하지 않고 그대로 사용한다.
함수 $F:N\rightarrow M$이 submanifold라는 것은 직관적으로 $F$가 inclusion $N\hookrightarrow M$의 역할을 하는 것으로 생각할 수 있다. 이 때, $F$의 image $F(N)\subseteq M$에 위상구조를 주는 방법은 두 가지가 있는데, 하나는 전단사함수 $F:N\rightarrow F(N)$을 통해 $N$의 위상을 옮겨오는 것이고, 다른 하나는 $M$에 주어진 위상구조를 subspace topology를 통해 가져오는 것이다. 만일 이 두 위상이 서로 동일하다면 $F$를 embedded submanifold라 부르는 것이고, 그렇지 않다면 이를 단순히 submanifold라 부른다.
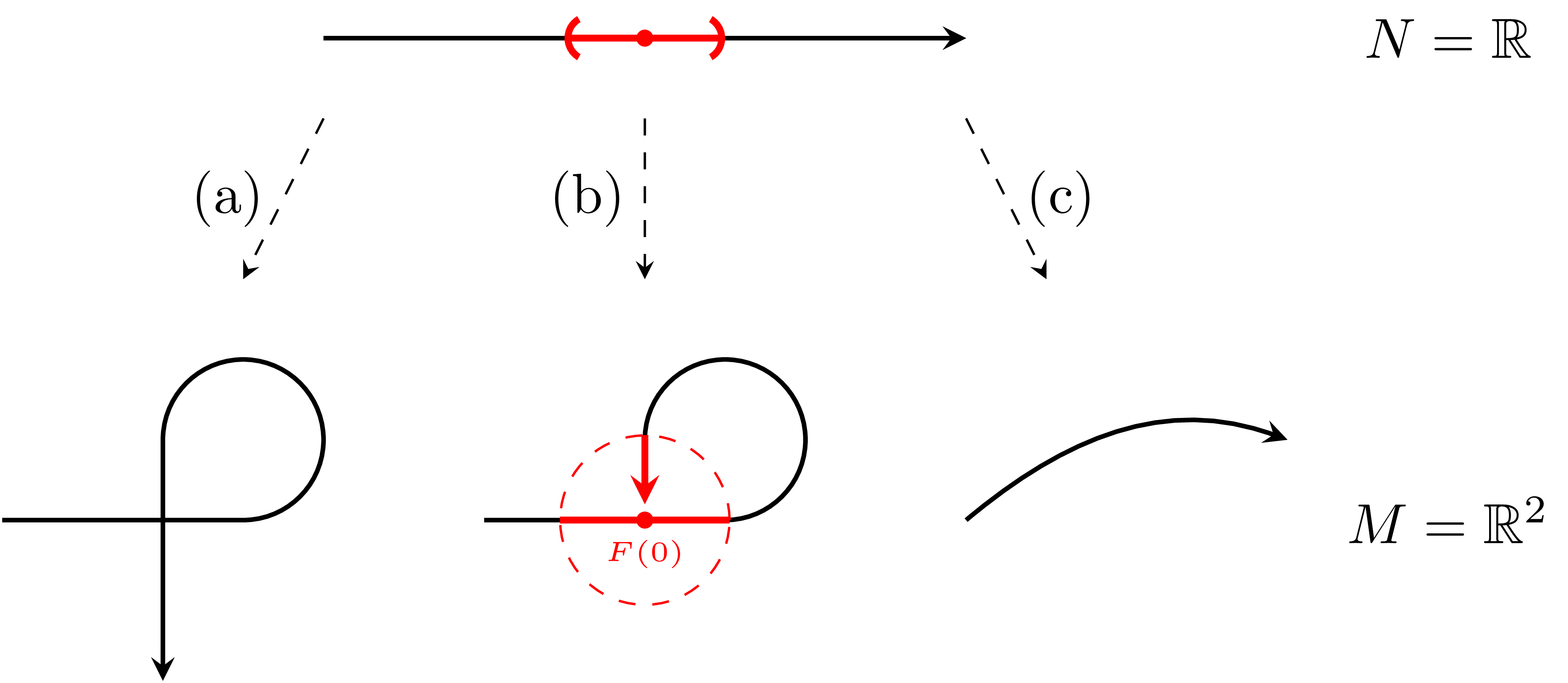
예를 들어, 위의 그림에서 $N=\mathbb{R}$, $M=\mathbb{R}^2$이며, (a)는 immersion이지만 submanifold는 아니고, (b)는 submanifold이지만 embedded submanifold는 아니며, (c)는 embedded submanifold이다. 편의상 (b)에서 $t\rightarrow \infty$일 때 $F(t)$가 향하는 점을 $F(0)$이라 하면, $\mathbb{R}$에서 $(-1,1)$은 열린집합이지만, $N$에 주어진 subspace topology 상에서 $F\bigl((-1,1)\bigr)$은 열린집합이 될 수 없다.
예시 2 Manifold $M$과 그 open submanifold $U$에 대하여, $\iota:U\hookrightarrow M$은 $M$의 embedded submanifold이다. 모든 $p\in U$에 대하여 $d\iota_p$가 injective라는 것은 $T_pU$와 $T_{\iota(p)}M$ 사이의 isomorphism이라는 사실로부터 명확하고, 또 open submanifold의 정의에 의해 $\iota(U)$에는 subspace topology가 주어져 있다.
예시 3 두 manifold $M,N$과 그 product $M\times N$을 생각하자. 그럼 임의의 $q\in N$에 대하여, 부분집합 $M\times\{q\}$은 $M$과 diffeomorphic한 $M\times N$의 embedded submanifold이고, 비슷하게 임의의 $p\in M$에 대하여 부분집합 $\{p\}\times N$은 $N$과 diffeomorphic한 embedded submanifold이며, 이 때의 embedding은 각각 $x\mapsto (x,q)$와 $y\mapsto (p,y)$으로 주어진다.
더 일반적으로 두 manifold $M,N$과, open submanifold $U\subseteq M$에서 정의된 $C^\infty$ 함수 $f:U\rightarrow N$이 주어졌다 하자. 그럼 $f$의 그래프
\[\graph(f)=\{(x,y)\in M\times N\mid x\in U, y=f(x)\}\]또한 embedded submanifold이며, 이 때 embedding은 당연히 $x\mapsto (x,f(x))$으로 주어진다.
역함수 정리와 그 결과들
이제 우리는 유클리드 공간에서의 역함수 정리와 음함수 정리를 각각 manifold의 단계로 가져올 것이다. 우선 유클리드 공간에서의 역함수 정리는 다음과 같다.
정리 4 (역함수 정리) $U\subset\mathbb{R}^m$이 열린집합이라 하고, $f:U\rightarrow\mathbb{R}^m$이 $C^\infty$ 함수라 하자. 임의의 점 $p_0\in U$에서 다음의 Jacobian matrix
\[\begin{pmatrix}\partial(r^1\circ f)/\partial r^1&\partial(r^1\circ f)/\partial r^2&\cdots&\partial(r^1\circ f)/\partial r^m\\\partial(r^2\circ f)/\partial r^1&\partial(r^2\circ f)/\partial r^2&\cdots&\partial(r^2\circ f)/\partial r^m\\\vdots&\vdots&\ddots&\vdots\\\partial(r^m\circ f)/\partial r^1&\partial(r^m\circ f)/\partial r^2&\cdots&\partial(r^m\circ f)/\partial r^m\end{pmatrix}\]가 nonsingular라면, $p_0\in V\subseteq U$를 만족하는 적당한 열린집합 $V$가 존재하여 $f|_V$가 $V$와 $f(V)$ 사이의 diffeomorphism을 정의한다.
이를 통해 일반적인 manifold 사이의 함수들에 대한 정리들을 증명할 수 있다.
따름정리 5 $F:M\rightarrow N$이 manifold들 사이의 $C^\infty$ 함수이고 $p\in M$이라 하자. 만일 $dF_p:T_pM\rightarrow T_{F(p)}N$이 isomorphism이라면 적당한 열린집합 $U\subseteq M$이 존재하여, $p\in U$이고 $F|_U:U\rightarrow F(U)$가 $U$와 $F(U)$ 사이의 diffeomorphism을 정의한다.
증명
우선 $dF_p$가 isomorphism인 것으로부터 $\dim M=\dim T_pM=\dim T_{F(p)}N=\dim N$을 얻는다. 이제 점 $F(p)$를 포함하는 coordinate system $(W,\tau)$를 잡고, $F(V)\subseteq W$를 만족하도록 $p$를 포함하는 coordinate system $(V,\varphi)$를 잡자. 그럼 함수 $(\tau\circ F\circ\varphi^{-1})|_{\varphi(V)}$는 같은 차원을 갖는 유클리드 공간 사이의 함수이며, 또 $dF_p$가 isomorphism인 것으로부터 이 함수의 점 $\varphi(p)$에서의 Jacobian matrix가 nonsingular라는 것을 안다.
따라서 역함수정리에 의해, $\varphi(p)\in U’\subset\varphi(V)$를 만족하는 열린집합 $U’$가 존재하여 $(\tau\circ F\circ\varphi^{-1})|_{U’}$이 $U’$와 $\tau\circ F\circ\varphi^{-1}(U’)$ 사이의 diffeomorphism을 정의한다. 이제 $U=\varphi^{-1}(U)$로 잡으면 함수
\[\tau^{-1}\circ\bigl((\tau\circ F\circ\varphi^{-1})|_{U'}\bigr)\circ\varphi\]가 $U$와 $F(U)$ 사이의 diffeomorphism을 정의한다.
Manifold $M$과 $p\in M$에 대하여, $C_p^\infty(M)$의 원소들 $y^1, \ldots, y^k$가 주어졌다 하자. 만일 이들의 differential $dy^i$들이 $T_p^\ast M$의 linearly independent인 부분집합이 된다면 이들을 점 $p$에서 independent한 함수들이라 한다.
따름정리 6 $m$차원 manifold $M$을 생각하자. 만일 $y^1, \ldots, y^m$들이 점 $p_0\in M$에서 independent라면, $(y^1, \ldots, y^m)$은 $p$ 근방에서 coordinate system이 된다.
증명
우선 $T_p^\ast M$의 차원을 생각하면 주어진 함수들의 differential이 $T_p^\ast M$의 basis가 된다는 것을 알 수 있다.
$m$개의 함수 $y^i$들이 모두 $p_0$의 열린근방 $U$에서 정의되었다 하자.1 주어진 것와 같이 $\varphi:U\rightarrow\mathbb{R}^m$을
\[\varphi(p)=(y^1(p),\ldots, y^m(p))\]으로 정의하면, 각각의 성분함수 $y^i$들이 모두 $C^\infty$이므로 $\varphi$도 $C^\infty$이다. 이제 $(d\varphi_{p_0})^\ast:T_{\varphi(p_0)}^\ast\mathbb{R}^m\rightarrow T_{p_0}^\ast M$을 생각하자. $(d\varphi_{p_0})^\ast$에 $dr^i|_{\varphi(p_0)}$들을 대입하면,
\[d\varphi_{p_0}\left(dr^i|_{\varphi(p_0)}\right)=\left(dr^i|_{\varphi(p_0)}\right)\circ\left(d\varphi_{p_0}\right)=d(r^i\circ\varphi)_{p_0}=dy^i|_{p_0}\]이므로, $T_{\varphi(p_0)}^\ast\mathbb{R}^m$에서의 basis $dr^i|_{\varphi(p_0)}$들이 모두 $T_{p_0}^\ast M$의 basis로 각각 옮겨지고 따라서 $(d\varphi_{p_0})^\ast$는 isomorphism이다. 따라서 $d\varphi_{p_0}$도 isomorphism이며, 따라서 따름정리 5를 적용하면 $p_0\in V\subseteq U$를 만족하는 적당한 $V$가 존재하여 $\varphi|_V:V\rightarrow\varphi(V)$가 coordinate system이 된다는 것을 알 수 있다.
위의 따름정리로부터 다음 두 따름정리들을 얻어내는 것은 본질적으로 학부 선형대수의 내용이다.
따름정리 7 $m$차원 manifold $M$과 $p_0\in M$, 정수 $0<k<m$에 대하여, $\mathcal{C}_{M,p_0}^\infty$의 원소들 $y^1,\ldots, y^k$가 $p_0$에서 independent한 함수들이라 하자. 그럼 적당한 함수 $x^{k+1},\ldots, x^{m}$들이 존재하여 $(y^1,\ldots, y^k, x^{k+1}, \ldots, x^m)$들이 $p_0$ 근방에서 coordinate system을 정의한다.
증명
점 $p_0$에 대한 coordinate system $(U,\varphi)$, $\varphi=(x^i)_{i=1}^{m}$이 주어졌다 하자. 그럼 $dx^i$들이 $T_{p_0}^\ast M$의 basis가 된다. 이제 [선형대수학] §백터공간의 차원, ⁋보조정리 2의 증명과 마찬가지로 $dy^i$들을 하나씩 넣고, $dx^j$들을 하나씩 빼며 적절히 index를 수정해주면 된다.
따름정리 8 $m$차원 manifold $M$과 점 $p_0\in M$에 대하여, $\mathcal{C}_{M,p_0}^\infty$의 원소들 $y^1,\ldots, y^k$들이 주어졌다 하자. 만일 $dy^i$들이 $T_{p_0}^\ast M$을 span한다면 집합 $\{y_1,\ldots, y_k\}$의 적절한 부분집합이 $p_0$ 근방의 coordinate system을 이룬다.
증명
$T_{p_0}^\ast M$의 basis를 이루는 집합 $\{dy^1,\ldots, dy^k\}$의 적절한 부분집합을 찾으면 이 부분집합은 반드시 $m$개의 원소로 이루어져 있다. 따라서 따름정리 6을 적용하면 된다.
다음 두 따름정리들은 앞으로 rank theorem이라는 이름으로 자주 사용하게 된다.
따름정리 9 (Rank theorem, Submersion case) 두 manifold $M,N$과 $C^\infty$ 함수 $F:M\rightarrow N$에 대하여, $dF_p$가 surjective라 하자. 그럼 점 $F(p)$ 근방에서 정의된 coordinate system $\psi=(y^j)_{j=1}^n$에 대하여 적당한 함수들 $x^{n+1},\ldots, x^m$이 존재하여 다음의 함수들
\[x^1=y^1\circ F,\quad x^2=y^2\circ F,\quad\ldots,\quad x^n=y^n\circ F,\qquad x^{n+1},\quad \ldots,\quad x^m\]이 $p$ 근방에서의 coordinate system을 이루도록 할 수 있다.
증명
$dF_p$가 surjective이므로, 그 dual $(dF_p)^\ast:T_{F(p)}^\ast N\rightarrow T_p^\ast M$은 injective이다. 즉, 다음의 원소들
\[(dF_p)^\ast(dy^i|_{F(p)})=dy^i|_{F(p)}\circ dF_p=d(y^i\circ F)_p=dx^j|_p\]이 $T_p^\ast M$에서 linearly independent하다. 따라서 따름정리 7에 의하여 원하는 결과를 얻는다.
따름정리 10 (Rank theorem, Immersion case) 두 manifold $M,N$과 $C^\infty$ 함수 $F:M\rightarrow N$에 대하여, $dF_p$가 injective라 하자. 그럼 점 $F(p)$ 근방에서 정의된 coordinate system $\psi=(y^j)_{j=1}^n$에 대하여, 다음 집합
\[\{x^j=y^j\circ F\mid j=1,\ldots, n\}\]의 부분집합이 점 $p$ 근방에서 $M$의 coordinate system을 이룬다.
증명
$dF_p$가 injective이므로, 그 dual $(dF_p)^\ast:T_{F(p)}^\ast N\rightarrow T_p^\ast M$은 surjective이다. 즉, 다음의 원소들
\[(dF_p)^\ast(dy^i|_{F(p)})=dy^i|_{F(p)}\circ dF_p=d(y^i\circ F)_p=dx^j|_p\]들이 $T_p^\ast M$을 span해야 하고, 따라서 따름정리 8에 의해 주어진 집합의 부분집합이 $p$ 근방에서 $M$의 coordinate system을 이룬다.
참고문헌
[War] Frank W. Warner. Foundations of Differentiable Manifolds and Lie Groups, Graduate texts in mathematics, Springer, 2013
[Lee] John M. Lee. Introduction to Smooth Manifolds, Graduate texts in mathematics, Springer, 2012
-
이는 $y^i$들이 유한 개이기 때문에 가능하다. 즉, $y^i$들이 각각 $U^i$에서 정의되었다면, $U=\bigcap U^i$로 잡으면 된다. ↩

댓글남기기