미분형식

벡터다발들

§접다발과 여접다발, ⁋예시 5와 §접다발과 여접다발, ⁋정리 6을 이용하면 다음을 정의할 수 있다.

정의 1 Manifold \(M\)에 대하여,

\[\mathcal{T}^{r,s}(M)=\mathcal{T}^{r,s}(TM),\quad \bigwedge\nolimits^\ast(M)=\bigwedge(T^\ast M),\quad \bigwedge\nolimits^k(M)=\bigwedge\nolimits^k(T^\ast M)\]

를 각각 \(M\) 위에서의 \((r,s)\)-tensor bundle, exterior algebra bundle, exterior \(k\)-bundle이라 부른다. 이들의 smooth section

\[\Gamma\left(\mathcal{T}^{r,s}(M)\right),\quad\Omega^\ast(M):=\Gamma\left(\bigwedge\nolimits^\ast(M)\right),\quad\Omega^k(M):=\Gamma\left(\bigwedge\nolimits^k(M)\right)\]

의 원소들을 각각 tensor field_텐서장, differential form_미분형식, differential \(k\)-form_{\(k\)차 미분형식}이라 부른다.

두 simple tensor

\[\omega=\alpha^1\otimes\cdots\otimes \alpha^r\otimes u_{r+1}\otimes\cdots\otimes u_{r+s}\in\mathcal{T}^{r,s}(T_p^\ast M),\quad u=u_1\otimes\cdots\otimes u_r\otimes \alpha^{r+1}\otimes\cdots\otimes \alpha^{r+s}\in\mathcal{T}^{r,s}(T_pM)\]

에 대하여,

\[(\omega,u)=\alpha^1(u_1)\alpha^2(u_2)\cdots \alpha^{r+s}(u_{r+s})\]

으로 정의하자. 그럼 \((-,-)\)은 non-degenerate pairing이므로 \(\mathcal{T}^{r,s}(T_p^\ast M)\cong\mathcal{T}^{r,s}(T_pM)^\ast\)이 성립한다. ([선형대수학] §쌍대공간, ⁋따름정리 5)

이와 유사하게, 두 원소

\[\omega=\alpha^1\wedge\cdots\wedge \alpha^k\in \bigwedge\nolimits^k(T_p^\ast M),\quad u=u_1\wedge\cdots\wedge u_k\in\bigwedge\nolimits^k(T_pM)\]

에 대하여 pairing \((-,-)\)을

\[(\omega, u)=\det\bigl(\alpha^i(u_j)\bigr)\]

으로 주면 \(\bigwedge\nolimits^k(T_pM)^\ast\cong\bigwedge\nolimits^k(T_p^\ast M)\)임을 확인할 수 있다. 한편 벡터공간들의 유한한 family \((V_i)_{1\leq i\leq n}\)에 대하여

\[\bigoplus_{i=1}^n V_i^\ast\cong \left(\bigoplus_{i=1}^n V_i\right)^\ast\]

이 성립하고, \(\bigwedge(V)\)는 오직 유한히 많은 \(\bigwedge\nolimits^k(V)\)들의 direct sum이므로

\[\bigwedge(T_p^\ast M)=\bigoplus_{k\geq 0}\bigwedge\nolimits^k(T_p^\ast M)=\bigoplus_{k\geq 0}\bigwedge\nolimits^k(T_pM)^\ast\cong\left(\bigwedge(T_pM)\right)^\ast\]

가 성립한다.

미분형식과 pullback

위의 정의 1 중 특히 \(\Omega^\ast(M)\)의 원소들이 관심의 대상이 된다. 정의에 의하여 임의의 differential form \(\omega\in\Omega^\ast(M)\)은 함수 \(M\rightarrow\bigwedge\nolimits^\ast(M)\)이며, 이 함수값을

\[p\mapsto \omega_p\in\bigwedge\nolimits^\ast(T_pM)\]

으로 적는다. 두 differential form들의 wedge product \(\omega\wedge\eta\)를 다음의 식

\[(\omega\wedge\eta)_p=\omega_p\wedge\eta_p\qquad\text{for all $p\in M$}\]

으로 정의하면 \(\Omega^\ast(M)\)은 \(\mathbb{N}\)-graded \(\mathbb{R}\)-algebra

\[\Omega^\ast(M)=\bigoplus_{k=0}^n\Omega^k(M)\]

으로 생각할 수 있다. 뿐만 아니라, \(\Omega^\ast(M)\)에서의 \(\mathbb{R}\)에 의한 스칼라곱은 사실 각 점 \(p\)마다 수행할 수 있기 때문에, \(\Omega^\ast(M)\)의 계수를 \(C^\infty(M)\)으로 생각할 수도 있다. 대수적으로 이는 ring homomorphism \(\mathbb{R}\rightarrow C^\infty(M)\)을 통해 coefficient ring을 바꾸어 주는 것으로 생각할 수도 있으며, 앞으로 \(\Omega^\ast(M)\)은 항상 이러한 식으로 \(\mathbb{N}\)-graded \(C^\infty(M)\)-algebra 구조가 주어진 것으로 생각한다.

이제 \(C^\infty\) 함수 \(F:M\rightarrow N\)이 주어졌다 하자. 그럼 linear map \(dF_p:T_pM\rightarrow T_{F(p)}N\)가 잘 정의된다. 따라서 \(dF_p\)의 dual map에 exterior algebra의 functoriality를 적용하면

\[\bigwedge({dF}_p^\ast):\bigwedge(T_{F(p)}^\ast N)\rightarrow\bigwedge(T_p^\ast M)\]

를 얻는다. ([다중선형대수학] §텐서대수, ⁋정의 10) 각 점 \(p\)마다 \(\bigwedge({dF}_p^\ast)\)를 대응시켜 얻은 linear map \(\Omega^\ast(N)\rightarrow\Omega^\ast(M)\)을 \(F^\ast\)로 적자. 즉 임의의 \(\omega\in\Omega^\ast(N)\)에 대하여

\[(F^\ast\omega)_p=\bigwedge({dF}_p^\ast)(\omega_{F(p)})\]

이다. 이렇게 얻어진 differential form \(F^\ast\omega\)를 \(\omega\)의 \(F\)에 의한 pullback_당김이라 부른다. 뿐만 아니라, \(F^\ast\)는 정의에 의하여 graded algebra homomorphism이므로 \(\wedge\) 또한 보존한다.

특별히 \(\omega\)가 \(k\)-form이라 가정하자. 점 \(p\in M\)에서 \((F^\ast\omega)_p\)를 계산하기 위해 \(k\)개의 벡터들 \(X_1(p),\ldots, X_k(p)\)를 대입하면

\[(F^\ast\omega)_p(X_1(p),\ldots, X_k(p))=(F^\ast_p\omega_{F(p)})\bigl(X_1(p),\ldots, X_k(p)\bigr)=\omega_{F(p)}\bigl(dF_p(X_1(p)), \ldots, dF_p(X_k(p))\bigr)\]

를 얻는다.

외미분과 드람 코호몰로지

앞서 우리는 \(\Omega^0(M)=C^\infty(M)\)인 것을 확인했다. 임의의 \(f\in C^\infty(M)\)에 대하여, 그 differential \(df\)는 각 점 \(p\in M\)을 받아 \(df_p:T_pM\rightarrow\mathbb{R}\)를 내놓는 함수이다. (§미분사상의 예시들, ⁋정의 6) 즉, \(df\in T^\ast M=\Omega^1(M)\)이다. 이 operator \(d\)는 다음과 같이 일반적인 differential form에 대해서도 정의된다.

정리 2 Manifold \(M\)에 대하여, degree \(1\)의 anti-derivation \(d:\Omega^\ast(M)\rightarrow\Omega^\ast(M)\)가 유일하게 존재하여 다음의 두 조건을 만족한다. (##ref##)

1. \(d^2=0\),
2. 임의의 \(f\in\Omega^0(M)\)에 대하여, \(df\)는 위와 같이 \(f\)의 differential과 동일하다.

뿐만 아니라, 이렇게 정의된 \(d\)는 pullback \(F^\ast\)와 commute한다.

이와 같이 differential \(d\)가 정의된 graded algebra를 differential graded algebra, 혹은 간단하게 DG-algebra라고 부른다. 한편 위의 조건 1에 의하여 다음 sequence

\[0\longrightarrow\Omega^0(M)\overset{d}{\longrightarrow}\Omega^1(M)\overset{d}{\longrightarrow}\Omega^2(M)\overset{d}{\longrightarrow}\cdots\overset{d}{\longrightarrow}\Omega^n(M)\longrightarrow 0\tag{2}\]

가 cochain complex가 된다. 또, \(d\)가 \(F^\ast\)와 commute하며, \(F^\ast\)는 graded algebra homomorphism이므로 위의 언어로는 \(F^\ast\)가 de Rham complex들 사이의 chain map을 유도한다고 이야기할 수 있다.

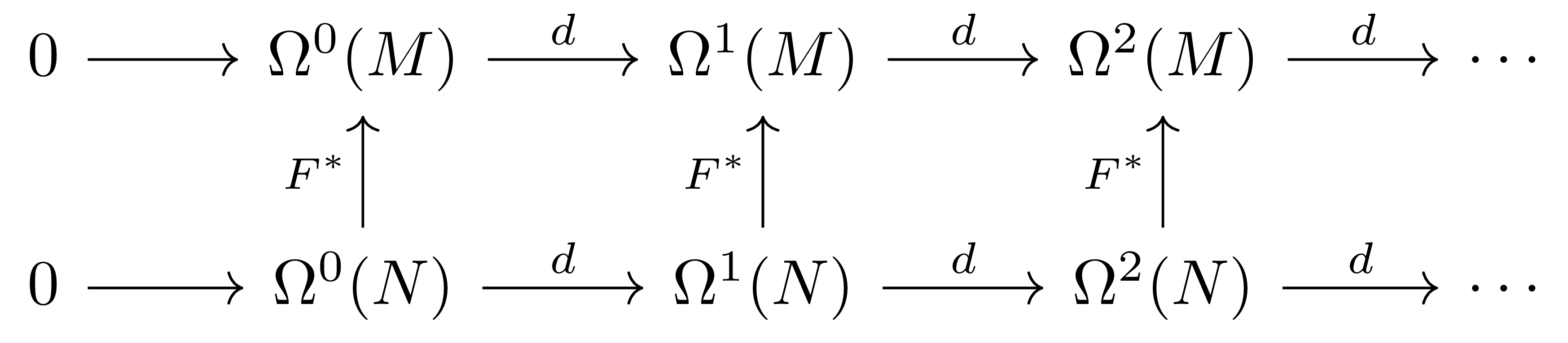
우리는 (2)의 cochain complex에 해당하는 homology group을 de Rham cohomology group_{드람 코호몰로지 군}이라 부르고 \(H^\ast_\text{dR}(M)\)으로 적는다. 드람 정리는 이렇게 얻어진 \(H_\text{dR}^\ast(M)\)이 위상적으로 정의한 다른 cohomology group들과 동일한 정보를 담고 있다는 것을 보여준다.

Interior multiplication

정의 3 Manifold \(M\) 위에 주어진 vector field \(X\)를 생각하자. 그럼 \(\iota_X:\Omega^\ast(M) \rightarrow\Omega^\ast(M)\)은 임의의 \(k\)-form \(\omega\)에 다음의 식

\[(\iota_X\omega)(X_1,\ldots, X_{k-1})=\omega(X,X_1,\ldots, X_{k-1})\]

으로 정의된 \((k-1)\)-form \(\iota_X\omega\)를 대응시키는 함수이다. 이를 \(X\)에 의한 interior multiplication_내부곱이라 부른다.

명제 4 Manifold \(M\)과 그 위에 주어진 임의의 vector field \(X\)에 대하여, interior multiplication \(\iota_X\)는 degree \(-1\)의 antiderivation이다.

---

참고문헌

[War] Frank W. Warner. Foundations of Differentiable Manifolds and Lie Groups, Graduate texts in mathematics, Springer, 2013
[Lee] John M. Lee. Introduction to Smooth Manifolds, Graduate texts in mathematics, Springer, 2012

---