우리는 이전 글에서 열심히 differential에 대한 내용을 공부했는데, 이제 이에 대한 예시를 살펴본다.
다양체에서의 곡선과 속도벡터
정의 1 Manifold $M$에 대하여, $C^\infty$ 함수 $\gamma:(a,b)\rightarrow M$을 $M$ 위에서 정의된 $C^\infty$ 곡선이라 부르고, 임의의 $t\in (a,b)$에 대하여
\[d\gamma_t\left(\frac{d}{dr}\bigg|_t\right)\]을 점 $\gamma(t)$에서 이 곡선의 속도벡터velocity vector라 부르고, $\gamma’(t)$로 표기한다.
벡터 $\gamma’(t)$는 $T_{\gamma(t)}M$의 원소로서 $\mathcal{C}^\infty_{M,\gamma(t)}$의 각 원소들 $f$에 작용하는데, differential의 정의를 풀어쓰면
\[\gamma'(t)f=d\gamma_p\left(\frac{d}{dr}\bigg|_t\right)f=\frac{d}{dr}\bigg|_t (f\circ\gamma)=\frac{d(f\circ \gamma)}{dr}(t)=(f\circ\gamma)'(t)\]임을 알 수 있다.
사실은 $T_pM$을 정의할 때, 이를 점 $p$를 지나는 $C^\infty$ 곡선들의 모임1으로 생각해도 큰 문제가 없다. 이 주장 중 일부인 다음의 명제는 사용할 일이 많으므로 증명을 해 둔다.
명제 2 Manifold $M$과 점 $p\in M$을 고정하자. 영벡터가 아닌 임의의 $v\in T_pM$에 대하여, 점 $p$를 지나고 점 $p$에서의 속도벡터가 $v$인 $C^\infty$ 곡선 $\gamma$가 존재한다.
증명
점 $p$를 중심으로 하고, 다음의 식
\[v=d\varphi^{-1}_{\varphi(p)}\left(\frac{\partial}{\partial r^1}\bigg|_0\right)\]을 만족하는 coordinate system $(U,\varphi)$를 찾으면 된다. 그럼 $v$는 $C^\infty$ 곡선
\[\gamma: t\mapsto \varphi^{-1}(t, 0,\cdots, 0)\]의 $t=0$에서의 속도벡터가 되기 때문이다. 참고로 위의 조건을 만족하는 coordinate system을 찾는 것은 아주 쉬운데, 임의의 coordinate system $(U,\psi)$를 하나 고른 후, $d\psi_p(v)$가 옮겨진 벡터를 포함하는 $\mathbb{R}^n$의 새로운 기저를 만든 후, 원래의 $\psi$와 이렇게 얻어진 change of basis를 합성하면 된다.
특별히 $M=\mathbb{R}^m$인 경우, $T_{\gamma(t)}M$의 basis는
\[\frac{\partial}{\partial r^1}\bigg|_{\gamma(t)},\cdots,\frac{\partial}{\partial r^m}\bigg|_{\gamma(t)}\]로 주어지므로,
\[\gamma'(t)=\sum_{i=1}^m\frac{d(r^i\circ \gamma)}{dr}(t)\frac{\partial}{\partial r^i}\bigg|_{\gamma(t)}=\frac{d\gamma^1}{dr}\frac{\partial}{\partial r^1}\bigg|_{\gamma(t)}+\cdots+\frac{d\gamma^m}{dr}\frac{\partial}{\partial r^m}\bigg|_{\gamma(t)}\]이고, 유클리드 공간에서는 이들 $\partial/\partial r^i$들이 $i$번째 standard basis와 같으므로 이를
\[\left(\frac{d\gamma^1}{dr},\ldots, \frac{d\gamma^m}{dr}\right)\]으로 생각할 수 있다. 이 식은 통상적인 다음의 미분
\[\gamma'(t)=\lim_{h\rightarrow 0}\frac{\gamma(t+h)-\gamma(t)}{h}\]와 동일하므로, 우리가 정의했던 tangent vector와 속도벡터의 개념이 유클리드 공간에서는 (원래부터 알고 있던) 곡선의 속도벡터와 일치한다는 것을 확인할 수 있다.
두 manifold $M,N$ 사이의 $C^\infty$ 함수 $F:M\rightarrow N$이 주어졌다 하고, $C^\infty$ 함수 $\gamma:(a,b)\rightarrow M$을 생각하자. 그럼 $F\circ\gamma$의 $t$에서의 differential을 계산해보면,
\[d(F\circ\gamma)_t=dF_{\gamma(t)}\circ d\gamma_t\]이고, 따라서
\[d(F\circ\gamma)_t\left(\frac{d}{dr}\bigg|_t\right)=(dF_{\gamma(t)}\circ d\gamma_t)\left(\frac{d}{dr}\bigg|_t\right)=dF_{\gamma(t)}(\gamma'(t))\]이다. 좌변을 $N$에서의 $C^\infty$ 곡선 $F\circ\gamma$의 시간 $t$에서의 속도벡터로 생각할 수 있으므로, 위의 식은
\[(F\circ\gamma)'(t)=dF_{\gamma(t)}(\gamma'(t))\]으로 적을 수 있다.
이를 약간 수정하면, 주어진 $C^\infty$ 함수 $F:M\rightarrow N$에 대하여, 임의의 $v\in T_pM$에서의 differential의 값 $dF_p(v)$를 알기 위해서는 점 $p$에서 $v$방향 속도벡터를 가지는 곡선을 아무거나 하나 고른 후2, 이 곡선 $\gamma$에 대해 $F\circ\gamma$의 시간 $t$에서의 속도벡터를 구하면 된다는 것을 알 수 있다. 즉,
명제 3 두 manifold $M,N$과 $C^\infty$ 함수 $F:M\rightarrow N$을 생각하자. 임의의 $v\in T_pM$에 대하여, $\gamma(0)=p$, $\gamma’(0)=v$를 만족하는 $C^\infty$ 곡선 $\gamma:(a,b)\rightarrow M$는 다음의 식
\[dF_p(v)=(F\circ\gamma)'(0)\]또한 만족한다.
벡터공간의 접공간
우리는 앞서 §미분다양체의 예시들, ⁋예시 2에서 임의의 $m$차원 $\mathbb{R}$-벡터공간 $V$가 $m$차원의 manifold 구조를 갖는다는 것을 살펴봤다. 그럼 임의의 점 $x\in V$에 대하여, 점 $x$에서의 tangent space $T_xV$ 또한 manifold $V$의 차원과 동일한 차원을 가지므로 $\dim T_xV=m$이 성립한다. 따라서 $V\cong T_xV$가 성립해야 한다.
이는 본질적으로 유클리드 공간에서 $\mathbb{R}^m$의 표준벡터들과, $T_x\mathbb{R}^m$의 basis들
\[\frac{\partial}{\partial r^1}\bigg|_x,\cdots,\frac{\partial}{\partial r^m}\bigg|_x\]이 동일한 것임을 이용하면 보일 수 있다. 사실 이 isomorphism은 basis의 선택에 의존하지 않는데, 임의의 $v\in\mathbb{R}^m$에 대하여
\[D_v|_x: f\mapsto \lim_{h\rightarrow 0}\frac{f(x+tv)-f(x)}{t}\]로 정의된 방향미분을 대응시키는 것이 이 isomorphism이기 때문이다.
명제 4 Manifold 구조가 주어진 $m$차원 $\mathbb{R}$-벡터공간 $V$를 생각하자. $V$의 임의의 점 $x\in V$에 대하여, basis의 선택에 의존하지 않는 isomorphism $V\cong T_xV$가 존재한다. 뿐만 아니라 $V,W$가 두 $\mathbb{R}$-벡터공간이고, $L:V\rightarrow W$가 linear map이라면 다음의 diagram이 commute한다.
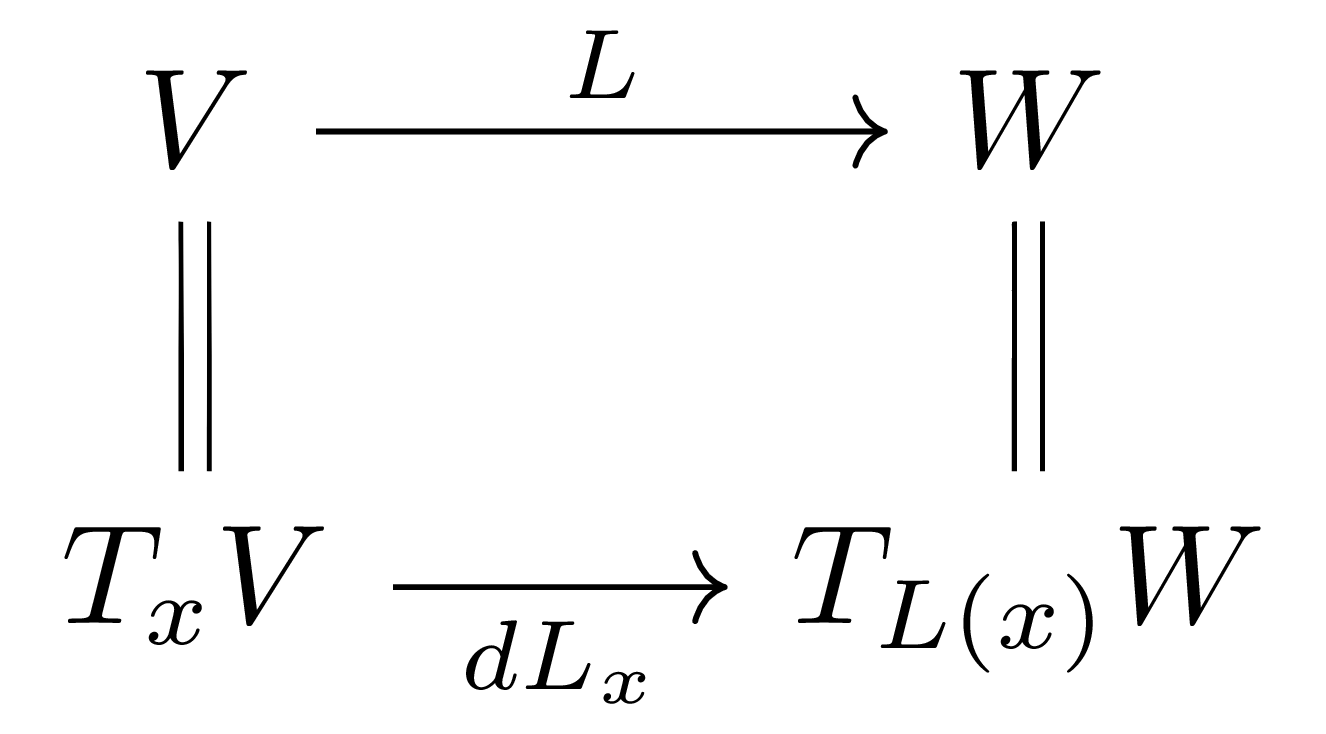
증명
첫 번째 부분은 앞서 보인 방향미분의 식
\[(D_v|_x)f=\lim_{t\rightarrow 0}\frac{f(x+tv)-f(x)}{t}\]을 사용하면 된다. 대응 $v\mapsto D_v|_x$에 의하여, $v+w$는
\[\begin{aligned}(D_{v+w}|_x)f&=\lim_{t\rightarrow 0}\frac{f(x+t(v+w))-f(x)}{t}\\ &=\lim_{t\rightarrow 0}\left(\frac{f((x+tw)+tv)-f(x+tw)}{t}+\frac{f(x+tv)-f(x)}{t}\right)\\ &=(D_v|_x)f+(D_w|_x)f \end{aligned}\]로 옮겨지며, 비슷하게 $\alpha v$는
\[(D_{\alpha v}|_x)f=\lim_{t\rightarrow 0}\frac{f(x+t\alpha v)-f(x)}{t}=\alpha\lim_{t\rightarrow 0}\frac{f(x+t\alpha v)-f(x)}{\alpha t}=\alpha(D_v|_x)f\]으로부터 얻어진다. 따라서 $v\mapsto D_v|_x$는 linear이다.
이 대응이 injective라는 것은 함수 $f$에 $x^1,\ldots, x^m$들을 대입해보면 되며, 두 벡터공간이 같은 차원을 가지므로 이 대응은 반드시 isomorphism이 되어야 한다. 이상에서 isomorphism $V\cong T_xV$를 얻었다.
두 번째 부분을 보여야 한다. 임의의 $v\in V$는 $V\rightarrow W\rightarrow T_{L(x)}W$를 따르면
\[v\mapsto L(v)\mapsto D_{L(v)}|_{L(x)}\]로 옮겨진다. 한편 $V\mapsto T_xV\mapsto T_{L(x)}W$를 따르면 우선 $V\mapsto T_xV$에 의하여
\[v\mapsto D_v|_x\]를 얻고, 이후에는 $\gamma(t)=x+tv$를 이용해 명제 3을 사용하면
\[dL_x(D_v|_x)=(L\circ \gamma)'(0)\]을 얻는다. 그런데
\[(L\circ\gamma)(t)=L(x+tv)=L(x)+tL(v)\]이므로, $(L\circ\gamma)’(0)$는 임의의 $f$에 대하여
\[(L\circ\gamma)'(0)f=\lim_{t\rightarrow 0}\frac{f(L(x)+tL(v))-f(L(x))}{t}=(D_{L(v)}|_{L(x)})f\]를 만족한다. 따라서 주어진 diagram이 commute한다.
위의 명제에서 만든 isomorphism $V\cong T_xV$는 basis의 선택에 의존하지 않지만, 만일 $V$의 어떤 basis $e_1,\ldots, e_n$과 그 dual basis $r^1,\ldots, r^n$이 주어진다면 이 isomorphism은
\[\sum a_ie_i\leftrightarrow\sum a_i\frac{\partial}{\partial r^i}\]과 같다는 것을 확인할 수 있다.
예시 5 $n\times n$ 행렬들의 모임 $\Mat_n(\mathbb{R})$은 $n^2$차원 $\mathbb{R}$-벡터공간이다. 따라서, $\Mat_n(\mathbb{R})$의 임의의 점에서의 tangent space는 $\Mat_n(\mathbb{R})$과 동일하다.
특별히 $\Mat_n(\mathbb{R})$의 open submanifold인 $\GL(n,\mathbb{R})$을 생각하면, $\GL(n,\mathbb{R})$의 임의의 원소에서의 tangent space는 이 원소를 $\Mat_n(\mathbb{R})$의 원소로 보았을 때의 tangent space와 동일하고, 따라서 $\Mat_n(\mathbb{R})$과 같다.
Tangent covector
임의의 manifold $M$과 $C^\infty$ 함수 $f:M\rightarrow\mathbb{R}$이 주어졌다 하자. 그럼 임의의 점 $p\in M$마다 differential $df_p:T_pM\rightarrow T_{f(p)}\mathbb{R}$이 잘 정의된다. 앞선 명제 4에 의하여, 1차원 $\mathbb{R}$-벡터공간으로서 $\mathbb{R}$과 그 tangent space $T_{f(p)}\mathbb{R}$ 사이의 isomorphism이 존재한다. 그럼 이제
\[T_pM\overset{df_p}{\longrightarrow}T_{f(p)}\mathbb{R}\overset{\sim}{\longrightarrow}\mathbb{R}\]에 의하여 $df_p$를 $(T_pM)^\ast$의 원소로 볼 수 있다.
정의 6 Manifold $M$과 한 점 $p\in M$에 대하여, $\mathbb{R}$-벡터공간 $T_pM$의 dual space $(T_pM)^\ast$를 cotangent space여접공간라 부르고 간단하게 $T_p^\ast M$으로 적는다. $T_p^\ast M$의 원소들을 tangent covector 혹은 간단하게 covector라 부른다.
따라서 앞선 논의는 임의의 $C^\infty$ 함수 $f:M\rightarrow\mathbb{R}$이 tangent covector를 하나 지정한다고 요약할 수 있다.
한편, $T_p^\ast M$은 벡터공간 $T_pM$의 dual space이고, $T_pM$은 유한차원 $\mathbb{R}$-벡터공간이므로 $T_pM$의 basis들이 $T_p^\ast M$의 dual basis를 정의한다.
$(U,\varphi)$가 점 $p$를 포함하는 coordinate system이라 하고, $\varphi=(x^i)_{i=1}^m$이라 하자. 그럼 다음의 $m$개의 tangent vector들
\[\frac{\partial}{\partial x^1}\bigg|_p,\cdots\frac{\partial}{\partial x^m}\bigg|_p\]이 $T_pM$의 basis가 된다. 이들의 dual basis를 잠시동안 $\xi^i |_p $라 표기하자. 즉 $\xi^i |_p $는 $T_pM$에서 $\mathbb{R}$로의 linear map이며, 다음의 식
\[(\xi^i |_p)\left(\frac{\partial}{\partial x^j}\bigg|_p\right)=\delta_{ij}\tag{1}\]을 통해 유일하게 정의된다. 이 때 $\delta_{ij}$는 크로네커 델타를 의미한다.
명제 7 위와 같은 상황에서, $\xi^i|_p=dx^i|_p$이다. 즉, $(U,\varphi)$에 의하여 생기는 $T_pM$의 dual basis $(\xi^i |_p)$들은 사실 coordinate function들 $x^i$의 점 $p$에서의 differential과 같다.
증명
$dx^i$들이 위의 식 (1)을 만족한다는 것을 보이면 충분하다. 정의에 의하여,
\[dx^i|_p\left(\frac{\partial}{\partial x^j}\bigg|_p\right)=\frac{\partial}{\partial x^j}\bigg|_p x^i=\delta_{ij}\]가 성립한다.
위 증명은 우리가 tangent space를 처음 도입할 때 증명했던 §여접공간, ⁋보조정리 1을 떠올리면 좀 더 그럴듯하다. 즉 첫째 등식에서 둘째 식으로 넘어가는 것은 differential $dx^i|_p$의 정의이기도 하지만, 동시에
\[T_p^\ast M\cong (\mathfrak{m}_p/\mathfrak{m}_p^2)^{\ast\ast}\cong\mathfrak{m}_p/\mathfrak{m}^2_p\]을 통해 유한차원 $\mathbb{R}$-벡터공간 $\mathfrak{m}_p/\mathfrak{m}^2_p$의 double dual을 자기 자신과 자연스럽게 identify하는 과정이기도 한 것이다.
참고문헌
[War] Frank W. Warner. Foundations of Differentiable Manifolds and Lie Groups, Graduate texts in mathematics, Springer, 2013
[Lee] John M. Lee. Introduction to Smooth Manifolds, Graduate texts in mathematics, Springer, 2012

댓글남기기