정의에 의하여, manifold $M$의 submanifold는 단사인 immersion을 의미한다. 이를 $\Phi:P\rightarrow M$으로 적자. 그럼 $\Phi$의 공역을 제한하여 얻어지는 함수 $\bar{\Phi}:P\rightarrow \Phi(P)$는 전단사함수이므로, $P$의 위상구조를 그대로 $\Phi(P)$ 위에 옮겨올 수 있고, 이러한 과정을 통해 $M$의 submanifold는 부분집합의 inclusion $\Phi(P)\hookrightarrow M$으로도 생각할 수 있다. 이번 글에서 우리는 이를 조금 더 자세히 살펴본다.
부분다양체와 $C^\infty$ 함수
우선 manifold $M$과, 그 submanifold $\Phi:P\rightarrow M$을 고정하자. 또 다른 $C^\infty$ 함수 $F:N\rightarrow M$이 $F(N)\subseteq\Phi(P)$를 만족한다 하면, 위와 같이 정의된 $\bar{\Phi}$를 사용하여 새로운 단사함수 $F_0:N\rightarrow P$를 다음의 식
\[F_0=\bar{\Phi}^{-1}\circ F\]을 통해 정의할 수 있다. 자연스럽게 이렇게 정의된 함수 $F_0$이 immersion이 되는지를 물어볼 수 있다.
Submanifold를 단순히 원래의 manifold의 부분집합으로 본다면, 이 질문은 단순히 임의의 $C^\infty$ 함수 $F:N\rightarrow M$의 치역이 $F(N)\subseteq P\subseteq M$을 만족할 때, $F$의 공역을 $P$로 제한한 것이 $C^\infty$냐는 질문과 같다. 그러나 이 질문은 보기보다 단순하지 않으며, 실제로 항상 이것이 성립하는 것은 아니다.
예시 1 두 manifold $N,P$가 모두 자연스러운 manifold 구조가 주어진 $\mathbb{R}$이라 하고, $M=\mathbb{R}^2$에도 자연스러운 manifold 구조가 주어졌다 하자. 두 submanifold $\Phi:N\rightarrow M$과 $\Psi:P\rightarrow M$을 다음의 두 그림

과

처럼 정의하자. 그럼 $\Phi(N)=\Psi(P)$이며, 따라서 $N$에서 $P$로의 전단사함수 $\bar{\Psi}^{-1}\circ\Phi$가 잘 정의된다.
이제 $N$에서 원점의 충분히 작은 열린근방 $U$를 생각하고, $U$의 $\bar{\Psi}^{-1}\circ\Phi$에 의한 image를 생각하면 $(\bar{\Psi}^{-1}\circ\Phi)(U)$는 $P$에서 열린집합이 아니다.
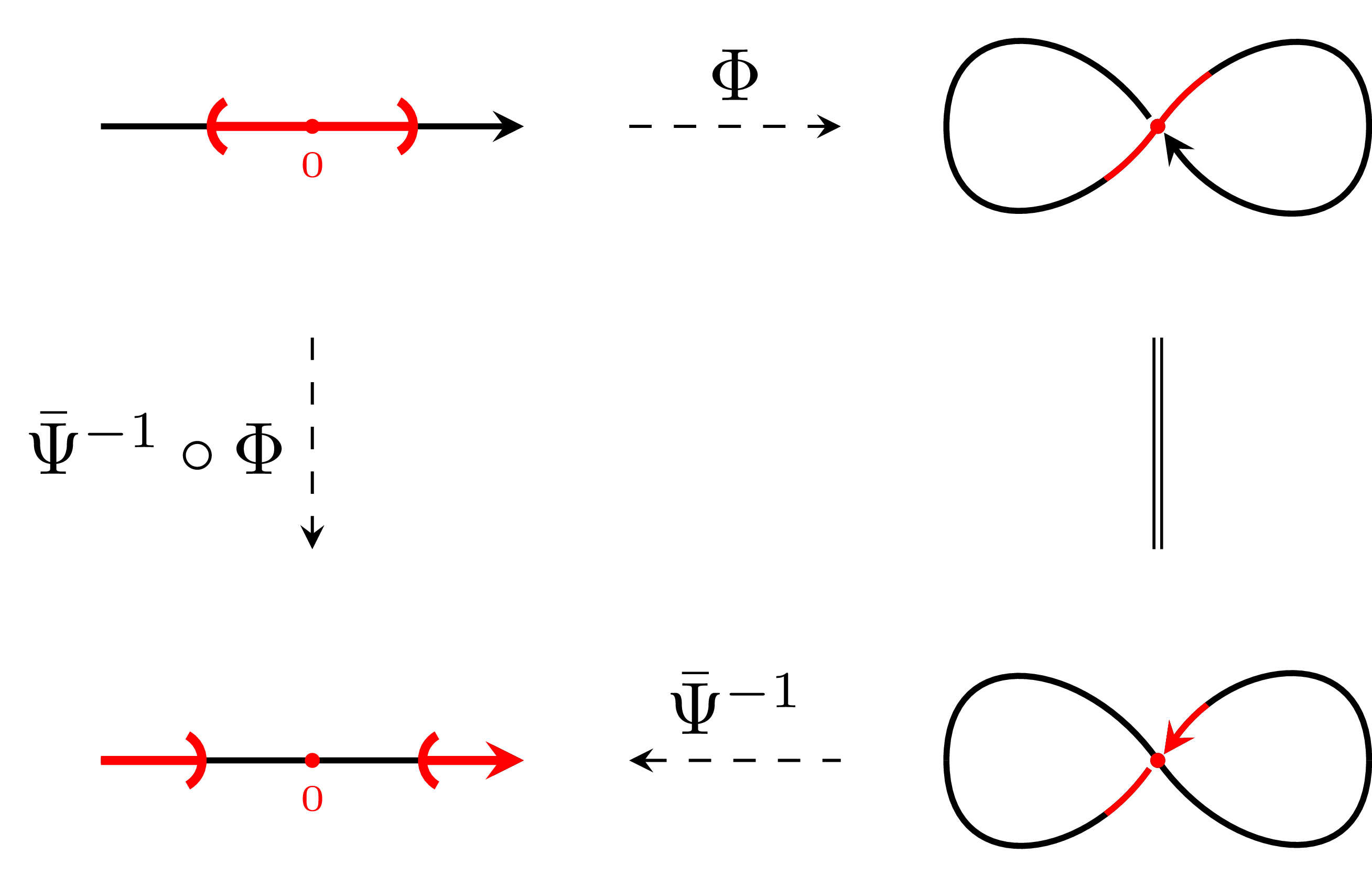
즉 $(\bar{\Psi}^{-1}\circ\Phi)^{-1}$이 연속이 아니므로 이 함수는 $C^\infty$ 함수조차 되지 않는다.
그러나, 다음 명제는 위의 예시와 같은 문제를 일으키는 것이 오직 위상적인 데이터라는 것을 보여준다.
명제 2 Manifold $M$의 submanifold $\Phi:P\rightarrow M$이 주어졌다 하자. 임의의 $C^\infty$ 함수 $F:N\rightarrow M$가 $F(N)\subseteq\Phi(P)$를 만족한다면, 다음의 식
\[F_0=\bar{\Phi}^{-1}\circ F\]을 통해 정의되는 함수 $F_0:N\rightarrow P$에 대하여 다음이 성립한다.
- 만일 $F_0$가 연속이라면 $F_0$은 $C^\infty$이다.
- 만일 $\Phi$가 embedding이라면 $F_0$은 연속이다.
증명
둘째 주장은 정의이므로 첫 번째 주장만 보이면 충분하다.
$F_0$가 연속이라 가정하고, $F_0$이 $C^\infty$이기도 하다는 것을 보이자. 즉 임의의 $x\in N$에 대하여, $x$를 중심으로 하는 coordinate system $(U,\varphi)$가 존재하여 $F_0$을 $U$로 제한한 것이 $C^\infty$임을 보여야 한다. 그런데 $F_0$가 연속인 전단사함수임을 가정하였으므로, 이를 보이기 위해서는 임의의 $y\in P$를 포함하는 coordinate system $(V,\psi)$가 존재하여, $\psi\circ F_0$을
이제 $y\in P$가 임의로 주어졌다 하고, $\Phi(y)$를 포함하는 $M$의 coordinate system $(W,z^1,\ldots, z^m)$를 택하자. 그럼 §부분다양체와 역함수 정리, ⁋따름정리 10으로부터 집합 $\{z^k\circ\Phi\mid 1\leq k\leq m\}$의 부분집합을 적당한 열린근방 $V$로 제한한 것이 점 $y\in P$의 coordinate system을 이룬다는 것을 안다.
이제 이들을 $\{z^1\circ\Phi,\ldots,z^p\circ\Phi\}$라 하자. 일반성을 잃지 않고, $\gamma=(z^1,\ldots, z^m)$이 $\mathbb{R}^m$으로의 전사함수라 하면, 위의 주장은 projection $\pi:\mathbb{R}^m\rightarrow\mathbb{R}^p$를 통해 $(V,\pi\circ\gamma\circ\Phi)$가 $y$의 coordinate system이 된다는 것과 동일한 말이다. 이제
\[(\pi\circ\gamma\circ\Phi)\circ F_0|_{F_0^{-1}(V)}=\pi\circ\gamma\circ F|_{F_0^{-1}(V)}\]이고, 우변의 식은 $C^\infty$ 함수들의 합성이므로 $C^\infty$이다.
부분다양체 사이의 동치관계
정의 3 Manifold $M$과 두 submanifold $\Phi_1:N_1\rightarrow M$, $\Phi_2:N_2\rightarrow M$이 주어졌다 하자. 이들 둘이 equivalent하다는 것은 diffeomorphism $\theta:N_1\rightarrow N_2$가 존재하여 $\Phi_1=\Phi_2\circ\theta$가 성립하는 것이다.
이렇게 정의된 관계가 $M$의 모든 submanifold들 $(N,\Phi)$들의 집합에 동치관계를 유도한다는 것은 자명하다. 임의의 equivalence class $[(N,\Phi)]$를 택하자. 그럼 처음에 살펴본 것과 같은 쌍
\[A=\Phi(N)\subseteq M, \qquad \iota:A\hookrightarrow M\]을 생각할 수 있다. 이 때, $A$는 전단사함수 $\bar{\Phi}:N\rightarrow A$을 통해 $N$의 미분구조와 위상구조가 부여된 manifold이다. 그럼 $\bar{\Phi}$는 $N$과 $A$ 사이의 diffeomorphism이므로, $\bar{\Phi}^{-1}$ 또한 diffeomorphism이고 따라서 합성
\[\iota=\Phi\circ\bar{\Phi}^{-1}\]은 $A$에서 $M$으로의 immersion이다. 즉 $(A,\iota)$는 $M$의 submanifold이다. 뿐만 아니라, 위의 식은 $(N,\Phi)$와 $(A,\iota)$가 equivalent하다는 것을 보여준다.
반대로, manifold 구조가 주어진 부분집합 $A\subseteq M$에 대하여 inclusion $\iota:A\hookrightarrow M$이 immersion이라 하면 $(A,\iota)$는 항상 $M$의 submanifold가 된다. 이는 임의의 $x\in A$에 대하여 $d\iota_x:T_xA\rightarrow T_xM$이 단사함수임을 의미하므로, $d\iota_x$는 $T_xA$와 $d\iota_x(T_xA)$ 사이의 전단사함수를 유도한다. 약간의 표기법 상의 문제를 덮어두면 $T_xA$를 $d\iota_x(T_xA)$와 동일한 것으로 취급할 수 있다.
부분다양체의 유일성
위의 절에서 정의한 $(A,\iota)$는 equivalence class $[(N,\Phi)]$마다
이 성립하므로 $A$는 유일하게 결정된다. 한편 이렇게 결정되는 $M$의 부분집합 $A$와 inclusion $\iota:A\hookrightarrow M$이 $[(N,\Phi)]$에 속하기 위해서는 $\iota=\Phi\circ\theta$를 만족하는 diffeomorphism $\theta$가 존재해야 하는데, 양 변의 왼쪽에 $\bar{\Phi}^{-1}$을 취해주면 $\theta=\bar{\Phi}^{-1}$이므로 $A$의 manifold 구조는
반면 manifold $M$의 임의의 부분집합 $\iota:A\hookrightarrow M$에 대하여, $(A,\iota)$를 submanifold로 만드는 $A$의 manifold 구조가 유일하게 존재하는 것은 아니다. 가령 예시 2와 같이 $M$의 두 submanifold $(N_1,\Phi_1),(N_2,\Phi_2)$가 서로 diffeomorphic하지 않지만 $\Phi_1(N_1)=\Phi_2(N_2)$를 만족한다면, $[(N_1,\Phi_1)]$과 $[(N_2,\Phi_2)]$에서 위의 과정을 통해 얻어지는 $(A,\iota)$ 위의 두 manifold 구조는 서로 달라야 한다.
그럼에도 불구하고, $(A,\iota)$가 만족해야 할 조건이 추가된다면 이 위에 submanifold의 구조가 유일하게 결정될 수도 있다. 다음 글에서 소개할 정리들의 결과는 이러한 유일성까지 만족하며, 이 때 다음의 두 명제를 유용하게 사용할 수 있다.
명제 4 Manifold $M$의 부분집합 $A$와, $A$ 위에 정의된 topology $\mathcal{T}$를 고정하자. 그럼 $(A,\iota)$를 $M$의 submanifold로 만드는 미분구조는 많아야 하나 존재한다.
증명
명제 2의 첫째 주장에 의해 자명하다.
명제 5 Manifold $M$의 부분집합 $A$가 주어졌다 하자. 만일 $A$를 $M$의 subspace로 보았을 때, $(A,\iota)$를 $M$의 submanifold로 만드는 미분구조가 존재한다면, 이 미분구조와 subspace topology는 $(A,\iota)$에 줄 수 있는 유일한 manifold의 구조가 된다.
증명
우선 앞선 명제 4를 subspace topology $\mathcal{T}$에 적용하면, $(A,\mathcal{T},\iota)$를 $M$의 submanifold로 만드는 미분구조는 유일하다. 이를 $\mathcal{A}$라 하자. 이제 $(A,\iota)$를 $M$의 submanifold로 만드는 위상 $\mathcal{T}’$와 미분구조 $\mathcal{A}’$가 주어졌다 하고, 다음 diagram을 생각하자.
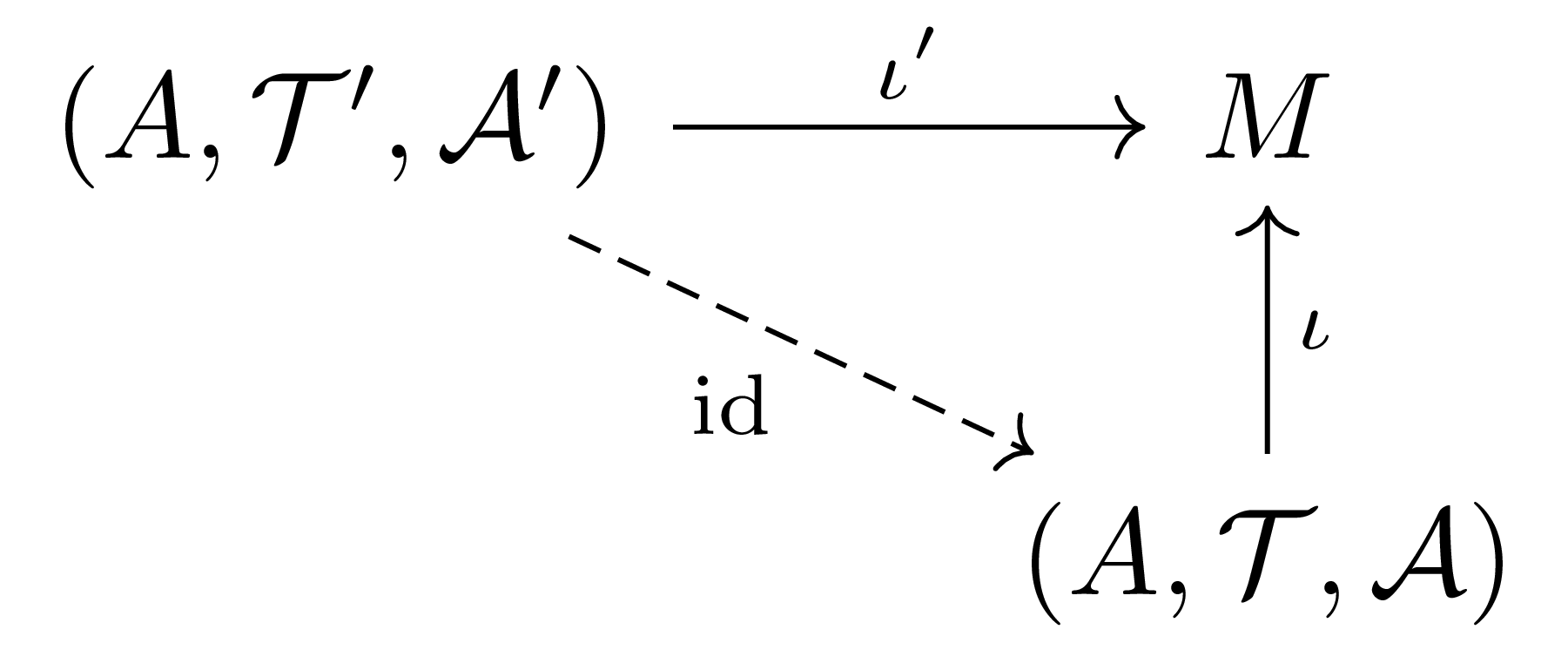
여기서 $\iota$와 $\iota’$는 모두 $A\hookrightarrow M$이지만, 구별을 위해 다른 이름으로 표기하였다. 정의에 의해 $(A,\mathcal{T},\mathcal{A})$가 $M$의 embedded submanifold이므로, 수직방향의 $\iota$는 embedding이고 따라서 명제 2에 의하여 $\operatorname{id}$는 $C^\infty$이다. 또, 연쇄법칙에 의하여
\[d\iota'=d\iota\circ d(\id)\]이 성립하고, $d\iota’$는 모든 점에서 단사이므로 $d(\id)$ 또한 모든 점에서 단사이다. 따라서 $d(\id)$가 모든 점에서 전사임을 보이면 충분하다.
결론에 반하여 $d(\id)$가 전사가 아닌 점 $a$가 존재한다 가정하자. 그럼 이 점에서의 tangent space의 차원을 생각하면
\[\dim(A,\mathcal{T}',\mathcal{A}')<\dim(A,\mathcal{T},\mathcal{A})\]이 성립한다. $(A,\mathcal{T},\mathcal{A})$의 차원을 $d$, $(A,\mathcal{T}’,\mathcal{A}’)$의 차원을 $d’$라 하자.
$(U,\varphi)$가 $(A,\mathcal{T},\mathcal{A})$의 coordinate system이라 하자. 일반성을 잃지 않고 $\varphi$의 image가 $\mathbb{R}^d$라 가정할 수 있으며, 이 때 $\id$는 전사함수이므로 합성 $\varphi\circ\id$의 image 또한 $\mathbb{R}^d$이다.
한편, $(A,\mathcal{T}’,\mathcal{A}’)$는 manifold이므로 이를 $\mathbb{R}^{d’}$와 homeomorphic한 countable한 coordinate system들 $(V,\sigma)$들로 덮을 수 있다. 그런데 $\varphi\circ\id\circ\sigma^{-1}$은 $C^\infty$이고, 이들은 $C^1$ 함수로서 모두 measure zero set $\mathbb{R}^{d’}$들을 measure zero set들로 보내므로 이들의 image가 $\mathbb{R}^d$가 되는 것은 모순이다.
참고문헌
[War] Frank W. Warner. Foundations of Differentiable Manifolds and Lie Groups, Graduate texts in mathematics, Springer, 2013
[Lee] John M. Lee. Introduction to Smooth Manifolds, Graduate texts in mathematics, Springer, 2012

댓글남기기