우선 다음을 정의하자.
정의 1 Manifold \(M\)과 coordinate system \((U,\varphi)\)가 주어졌다 하자. 이 때 \(\varphi=(x^i)_{i=1}^m\)이고, \(0\leq k\leq m\)라 하고, \(p\in \varphi(U)\)에 대해 다음의 집합
\[S=\{q\in U\mid x^i(q)=r^i(p), k+1\leq i\leq m\}\]에 subspace topology와 coordinate system \((S, (x^j\vert_S)_{j=1}^k)\)이 부여된 manifold를 \((U,\varphi)\)의 slice라 부른다.
보조정리 2 두 manifold 사이의 immersion \(F:M\rightarrow N\)이 주어졌다 하자. 그럼 임의의 \(p\in M\)이 주어질 때마다, \(F(p)\)를 포함하는 coordinate system \((V,\varphi)\)와 \(p\)의 적당한 열린근방 \(U\)가 존재하여 \(F\vert_U\)가 injective이고, \(F(U)\)가 \((V,\varphi)\)의 slice이도록 할 수 있다.
증명
위의 보조정리에서, \(M\)의 열린집합 \(U\)에 대하여 \(F(U)\)가 \((V,\varphi)\)의 slice가 된다는 것을 신경써서 볼 필요가 있다. 예를 들어, \(F(M)\cap V\)는 일반적으로 slice가 될 필요가 없으며, 이는 심지어 \(F\)가 submanifold일 경우에도 마찬가지이다.
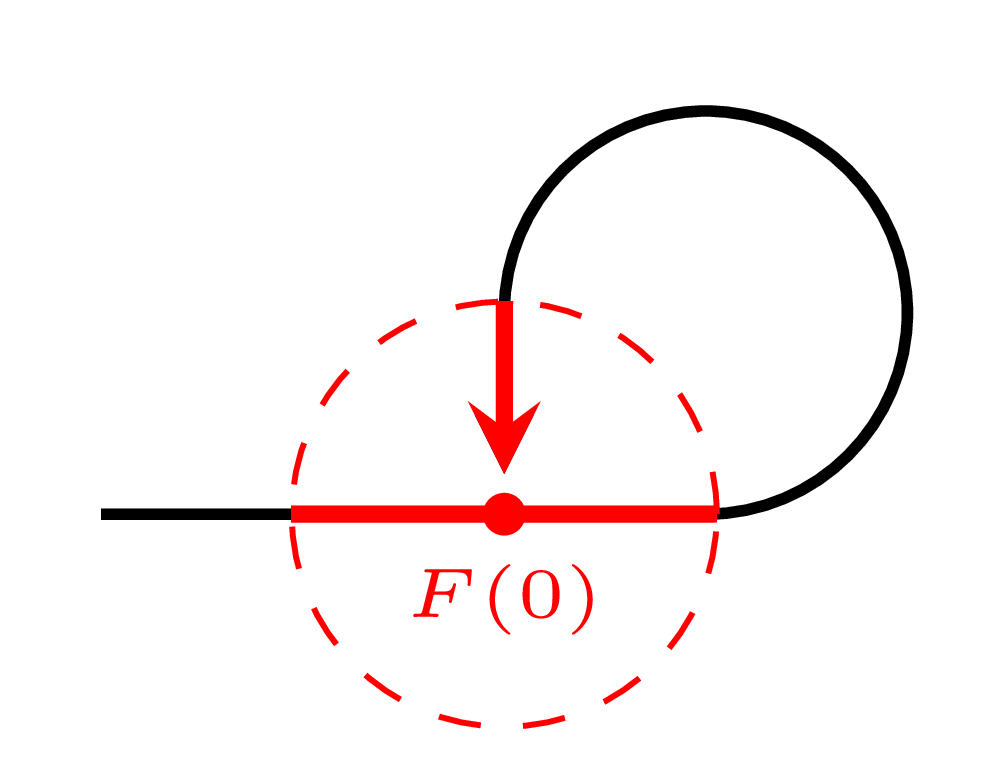
하지만 만일 \(M\)이 embedding이었다면 \((V,\varphi)\)를 적당히 잡아 \(F(M)\cap V\)가 \(V\)의 slice가 되도록 할 수 있다. 이러한 관점에서 위 보조정리를
Immersed submanifold는 locally embedded이다
정도로 요약할 수 있다.
음함수 정리와 그 결과들
이제 우리는 음함수 정리를 미분다양체로 확장할 준비가 되었다.
정리 3 (음함수 정리) \(U\subset\mathbb{R}^{m-n}\times\mathbb{R}^n\)이 열린집합이라 하고, 구별을 위해 \(\mathbb{R}^{m-n}\)의 좌표들을 \(r^1,\ldots, r^{m-n}\), 그리고 \(\mathbb{R}^n\)의 좌표들을 \(s^1,\ldots, s^n\)이라 하자. 또, \(f:U\rightarrow\mathbb{R}^n\)이 \(C^\infty\)이고, 어떤 점 \((x_0, y_0)\in U\)에 대하여 \(f(x_0,y_0)\)이라 하자. 만일 점 \((x_0,y_0)\)에서 Jacobian matrix
\[\begin{pmatrix}\partial f^1/\partial r^1&\partial f^1/\partial r^2&\cdots&\partial f^1/\partial r^{m-n}&\partial f^1/\partial s^1&\partial f^1/\partial s^2&\cdots&\partial f^1/\partial s^n\\\partial f^2/\partial r^1&\partial f^2/\partial r^2&\cdots&\partial f^2/\partial r^{m-n}&\partial f^2/\partial s^1&\partial f^2/\partial s^2&\cdots&\partial f^2/\partial s^n\\ \vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\ddots&\vdots\\\partial f^n/\partial r^1&\partial f^n/\partial r^2&\cdots&\partial f^n/\partial r^{m-n}&\partial f^n/\partial s^1&\partial f^n/\partial s^2&\cdots&\partial f^n/\partial s^n\end{pmatrix}\]의 \(n\times n\) submatrix
\[\begin{pmatrix}\partial f^1/\partial s^1&\partial f^1/\partial s^2&\cdots&\partial f^1/\partial s^n\\\partial f^2/\partial s^1&\partial f^2/\partial s^2&\cdots&\partial f^2/\partial s^n\\\vdots&\vdots&\ddots&\vdots\\\partial f^n/\partial s^1&\partial f^n/\partial s^2&\cdots&\partial f^n/\partial s^n\end{pmatrix}\]가 nonsingular라면, \(x_0\)의 적당한 열린근방 \(V\), \(y_0\)의 적당한 열린근방 \(W\), 그리고 \(C^\infty\) 함수 \(g:V\rightarrow W\)가 존재하여 \(V\times W\subseteq U\)이고, 각각의 \((p,q)\in V\times W\)마다
\[f(p,q)=0\iff q=g(p)\]를 만족한다.
따름정리 4 (Submersion level set theorem) \(F:M\rightarrow N\)이 \(C^\infty\)라 하고, \(q\in F(M)\)를 고정하고 \(P=F^{-1}(q)\)라 하자. 만일 임의의 \(p\in P\)마다 \(dF_p:T_pM\rightarrow T_{F(p)}N\)이 surjective라면, \(P\) 위에 정의된 유일한 manifold 구조가 존재하여 canonical injection \(\iota:P\hookrightarrow M\)이 submanifold가 된다.
또, 이 때 \(\iota\)는 embedding이고, \(P\)의 codimension \(\dim M-\dim P\)가 \(\dim N\)과 동일해진다.
증명
다음 따름정리의 가정은 앞선 따름정리의 가정보다 약하기 때문에 더 잘 사용할 수 있다.
따름정리 5 (Constant-rank level set theorem) \(F:M\rightarrow N\)이 \(C^\infty\)라 하고, 각각의 \(p\in P\)마다 정의되는 \(dF_p:T_pM\rightarrow T_{F(p)}N\)이 모든 점 \(p\in P\)에서 같은 rank를 가진다고 하자. 그럼 \(F:M\rightarrow N\)은 embedded submanifold이다.
이 정리들을 통해 주어진 manifold \(M\)의 특정한 부분집합이 embedded submanifold라는 것을 보일 수 있는데, 이는 대표적으로 다음과 같은 논증을 따른다.
예시 6 \(\mathbb{R}^{n+1}\)에서 \(\mathbb{R}\)로의 함수
\[f(x)=\lvert x\rvert^2=\sum_{i=1}^{n+1} r^i(x)^2\]를 생각하자. 임의의 점 \(x\in \mathbb{R}^{n+1}\)과 \(v\in T_x\mathbb{R}^{n+1}\)에 대하여,
\[df_x(v)=v(f)=\sum v^i\frac{\partial f}{\partial r^i}\bigg|_{x}=2\sum r^i(x) v^i\]이 성립하며, 이로부터 \(x\)가 원점이 아니라면 \(v\)를 조절하여 \(df_x(v)\)가 임의의 실수값을 갖도록 할 수 있음을 안다. 즉, \(df_x\)가 원점을 제외하면 항상 surjective이므로, \(f^{-1}(1)\)이 \(\mathbb{R}^{n+1}\)의 submanifold이도록 하는 유일한 manifold 구조가 존재한다. 유일성에 의하여 이 구조는 \(S^n\)에 주어진 manifold 구조와 동일하며, 다시 따름정리 5에 의해 이 구조는 \(\mathbb{R}^{n+1}\)의 embedded submanifold임을 알 수 있다.
참고문헌
[War] Frank W. Warner. Foundations of Differentiable Manifolds and Lie Groups, Graduate texts in mathematics, Springer, 2013
[Lee] John M. Lee. Introduction to Smooth Manifolds, Graduate texts in mathematics, Springer, 2012

댓글남기기