이제 우리는 행렬식을 정의할 것인데, 이를 위해 우선 텐서대수와 대칭대수, 외대수를 정의한다. 이 과정에서 \(A\)는 항상 commutative ring인 것으로 생각한다. 그럼 특히 \(A\)는 IBN property를 갖는다. (§기저, ⁋명제 6)
텐서대수의 정의
우리는 임의의 \(A\)-module \(M\)에 대하여, \(M\)에 의해 정의되는 free algebra \(F(M)\)을 다음의 식
\[F(M)=\bigoplus_{n\geq 0} M^{\otimes n}\]으로 정의했었다. ([대수적 구조] §대수, ⁋명제 4) 이는 단순한 algebra일 뿐 아니라, 자연스럽게 \(\mathbb{N}_{\geq 0}\)-graded associative unital algebra의 구조를 갖는다. 이를 다음과 같이 이름붙인다.
정의 1 위에서 정의한 \(F(M)\)을 \(M\)의 tensor algebra텐서대수라 부르고, \(\T(M)\)으로 표기한다.
이들 각각의 성분 \(M^{\otimes n}\)을 \(\T^n(M)\)으로 표기하기로 한다. 그럼 \(\T^1(M)=M\)이므로, \(M\)에서 \(\T(M)\)으로의 canonical injection \(\iota: M \rightarrow \T(M)\)이 존재한다.
이제 adjoint \(T\dashv U\)를 생각하면, \(\iota\)는 다음 adjunction
\[\Hom_{\Alg{A}}(\T(M), \T(M))\cong \Hom_{\rMod{A}}(M, U\T(M))\]에 의한 \(\id_{\T(M)}\)의 image이고, \(\T(M)\)을 \(\mathbb{N}\)-graded associative unital algebra로 보면 좌변을 적절한 category로 바꿔주면 된다. 이 adjoint를 universal property로 풀어쓰면 다음과 같다.
명제 2 임의의 \(A\)-algebra \(E\)와 \(A\)-linear map \(u:M \rightarrow E\)가 주어졌다 하자. 그럼 유일한 \(A\)-algebra homomorphism \(g: \T(M) \rightarrow E\)가 존재하여 \(f=g \circ\iota\)이도록 할 수 있다.
추가로, 만일 \(E\)가 \(\mathbb{N}\)-graded \(A\)-algebra이고, \(u(M)\subseteq E_1\)이 성립한다면 위에서 얻어지는 \(A\)-algebra homomorphism \(g\)는 \(\mathbb{N}\)-graded \(A\)-algebra homomorphism이 된다.
만일 위의 linear map \(u\)가 surjective라면, \(\T(N)\)이 \(\T^1(N)\)으로 생성되는 것으로부터 \(\T(u): \T(M) \rightarrow \T(N)\)이 surjective가 되는 것을 안다.
탠서대수의 성질들
이제 우리는 \(\rMod{A}\)에서의 연산들이 functor \(T:\rMod{A} \rightarrow \Alg{A}\)를 통해 옮겨졌을 때, 이들이 어떻게 행동하는지를 살펴본다. 특히 direct sum과 extension of scalar에 관심이 있다. 이 절의 논의는 명제 2와 같이, \(T\)를 \(\rMod{A}\)에서 associative unital \(\mathbb{N}\)-graded \(A\)-algebra들의 category들로 가는 functor로 이해하여도 동일한 논증이 성립하지만, 표기상의 복잡함을 해소하기 위해 target category를 \(\Alg{A}\)로 적기로 한다.
우선 direct sum의 경우를 살펴본다. \(M=\bigoplus_{i\in I} M_i\)가 \(A\)-module들 \(M_i\)들의 direct sum이라 하자. 그럼 \(\otimes\)가 \(\Hom\)의 left adjoint라는 사실과 약간의 귀납법을 통해 다음의 isomorphism
\[\bigoplus_{(i_1,\ldots, i_n)\in I^n}M_{i_1}\otimes\cdots\otimes M_{i_n}\cong \T^n(M)\]을 얻고, 그럼 \(\T(M)\)은 이들의 direct sum
\[\T(M)\cong\bigoplus_{n\geq 0} \T^n(M)\cong\bigoplus_{n\geq 0}\bigoplus_{(i_1,\ldots, i_n)\in I^n}M_{i_1}\otimes\cdots\otimes M_{i_n}\]으로 주어진다. 이는 식으로는 복잡해보이지만, 기본적으로는 \(T\)가 left adjoint이므로
\[T\left(\bigoplus_{i\in I} M_i\right)\cong \coprod_{i\in I} \T(M_i)\]로부터, 우변의 graded algebra들의 coproduct를 풀어쓴 것에 불과하다.1
특별히 임의의 free \(A\)-module \(M\)에 대하여, \(M\)의 basis를 \(\mathcal{B}=(e_i)_{i\in I}\)라 하자. 그럼
\[M=\bigoplus_{i\in I} Ae_i\]이며, 위의 설명을 적용하면 다음 명제를 얻는다.
명제 3 위와 같은 상황에서, \(\T(M)\)은 다음의 꼴
\[e_s=e_{i_1}\otimes\cdots\otimes e_{i_n},\qquad\text{$s$ a finite sequence $(i_1,i_2,\ldots,i_n)$ in $I$}\]들의 원소 \(e_s\)를 basis로 갖는다.
이는 \(\T^n(M)\) 각각이 길이 \(n\)짜리 유한한 수열 \(s\)를 사용해 정의한 \(e_s\)들을 basis로 갖고, 이들의 direct sum이 \(\T(M)\)이기 때문이다. 한편 우리는 §기저, ⁋정의 9의 structure constant를 사용하면 \(\T(M)\)의 곱셈을 서술할 수 있다는 것을 알고 있는데, 위의 설명에 따르면 이는 다른 것이 아니라 단순히 수열을 이어쓰기하여 얻어지는 것이다. 즉 두 수열
\[s=(i_1,\ldots, i_m),\qquad t=(j_1,\ldots, j_n)\]에 대하여, \(st\)를 다음의 수열
\[st=(i_1,\ldots, i_m,j_1,\ldots, j_n)\]으로 정의하면 structure constant를 정의하는 식은 다음의 식
\[e_se_t=e_{st}\]이 된다.
Extension of scalar의 경우, ring homomorphism \(\phi: A \rightarrow B\)가 주어졌다 하고, \(M\)이 \(A\)-module이라 하자. 그럼 extension of scalar \(\phi_!: \rMod{A} \rightarrow\rMod{B}\)와 두 functor \(\T_A: \rMod{A} \rightarrow \Alg{A}\), \(\T_B:\rMod{B} \rightarrow \Alg{B}\)가 존재하며, 자명한 방식으로 \(\phi_!:\Alg{A} \rightarrow\Alg{B}\) 또한 정의된다. 이를 통해 다음의 (graded) \(B\)-linear map
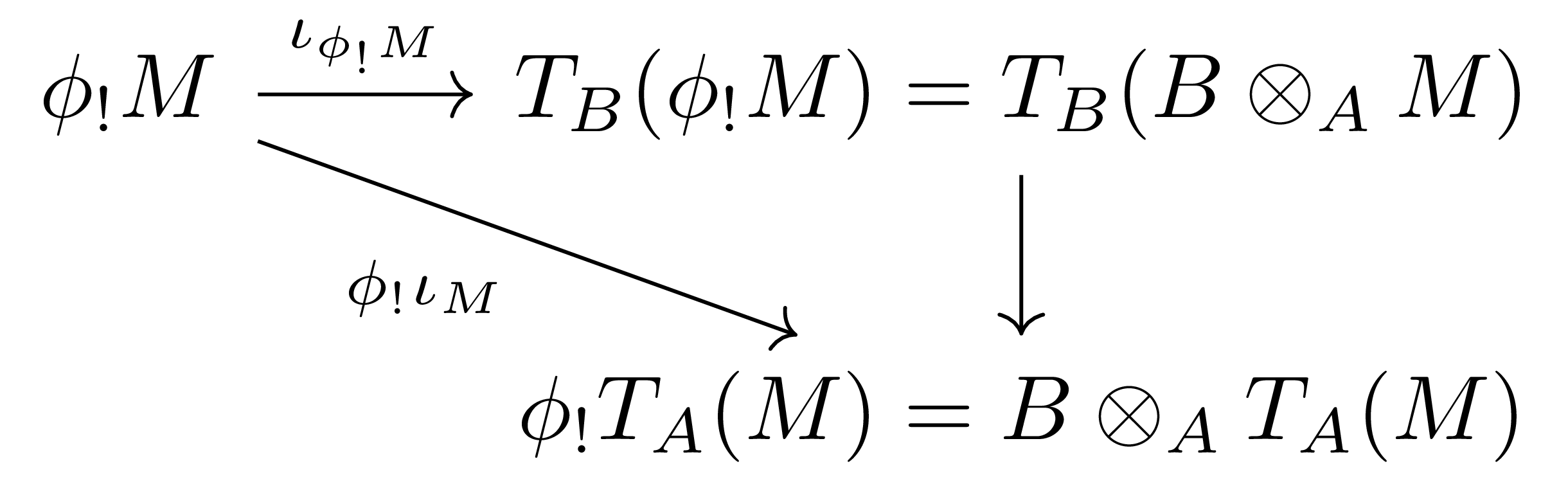
을 얻는다.
명제 4 위에서 얻어지는 \(B\)-linear map \(\T_{B}(B\otimes_AM)\rightarrow B\otimes_A\T_A(M)\)은 isomorphism이다.
증명
역함수를 만들면 충분하다. 이를 위해, 우선 adjoint
\[\Hom_\rMod{B}(\phi_!M,\phi_!M)\cong\Hom_\rMod{A}(M, \phi^\ast \phi_!M)\]로부터 \(\id_{\phi_!M}\)에 해당하는 \(A\)-linear map \(i: M \rightarrow \phi^\ast\phi_!M\)을 얻자. ([대수적 구조] §스칼라의 변환, ⁋명제 5) 그 후, \(A\)-module \(\phi^\ast\phi_!M\)을 \(B\)-module \(\phi_!M\)으로 본 후
\[\iota_{\phi_!M}: \phi_!M \rightarrow \T_B(\phi_!M)\]을 생각하면 이는 \(A\)-module \(M\)에서 \(A\)-module \(\phi^\ast \T_B(\phi_!M)\) (더 정확히는 \(U\phi^\ast \T_B(\phi^\ast\phi_!M)\))으로의 \(A\)-linear map이다. 따라서 명제 2에 의하여 다음의 diagram
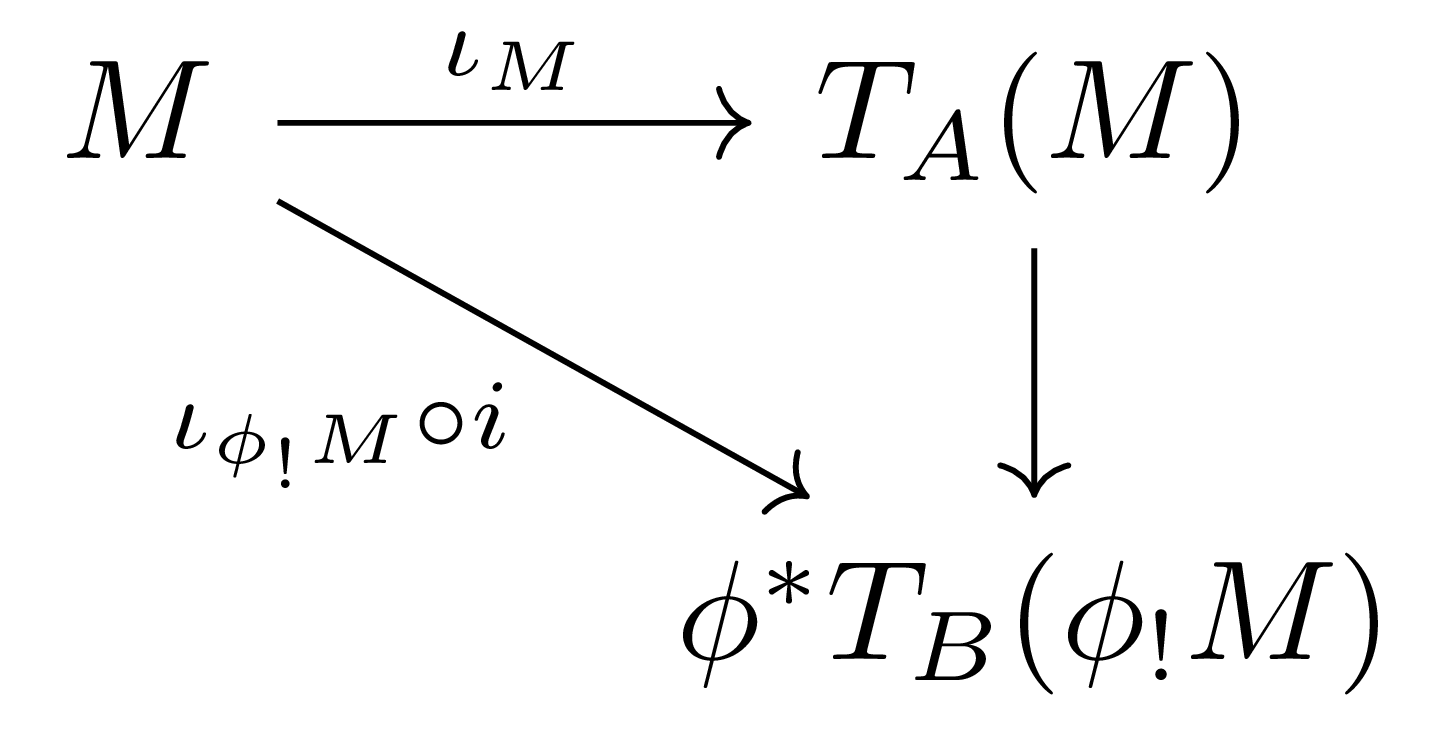
을 commute하도록 하는 \(A\)-algebra homomorphism \(T_A(M)\rightarrow \phi^\ast T_{B}(\phi_!M)\)이 유일하게 존재한다. 이제 다음의 adjoint
\[\Hom_{\Alg{A}}(\T_A(M), \phi^\ast \T_B(\phi_!M))\cong \Hom_\Alg{B}(\phi_! \T_A(M), \T_B(\phi_!M))\]에 의하여 이를 \(B\)-linear map \(\phi_!\T_A(M) \rightarrow \T_B(\phi_!M)\)으로 보면 이것이 위의 \(B\)-linear map의 inverse가 되는 것을 확인할 수 있다.
Mixed tensor
이제 free \(A\)-module \(M\)을 고정하고, \(M\oplus M^\ast\)의 tensor algebra \(\T(M\oplus M^\ast)\)를 생각하면, 명제 3의 결과로부터 \(\T^n(M\oplus M^\ast)\)는
아 이게 애매하네… tensor field를 저걸로 정의하면 깔끔할 것 같은데 저럼 순서가 다르면 다른걸로 취급하게 되니까… 암튼 이걸 해결한다면 contraction 먹여서 죽이는거 설명하면 될거같다
대칭대수의 정의
정의 5 임의의 \(A\)-module \(M\)에 대하여, tensor algebra \(\T(M)\)의 two-sided ideal
\[\mathfrak{I}=\langle x\otimes y-y\otimes x\mid x,y\in M\rangle\]을 생각하자. 그럼 quotient algebra \(\T(M)/\mathfrak{I}\)를 \(M\)의 symmetric algebra대칭대수라 부르고 \(\S(M)\)으로 적는다.
정의로부터 \(\mathfrak{I}\)는 homogeneous ideal이므로 \(\T(M)/\mathfrak{I}\)가 \(\mathbb{Z}_{\geq 0}\)-graded ideal이 되는 것은 자명하다. 또, 각각의 generator들 \(x\otimes y-y\otimes x\)는 모두 degree \(2\)의 원소이므로, \(\mathfrak{I}\)로 quotient를 취하는 것은 \(\T^0(M)\)과 \(\T^1(M)\)에는 아무런 영향을 미치지 않는다. 즉, \(\S^0(M)\cong A\)이고 \(\S^1(M)\cong M\)이다.
정의로부터 \(\S(M)\)이 commutative unital associative algebra인 것은 자명하다. 이는 \(\S(M)\)이 \(\S^1(M)\)의 원소들로 생성되는데, 임의의 \(x,y\in \S^1(M)\cong M\)에 대해서는
\[x\otimes y\equiv y\otimes x\pmod{\mathfrak{I}}\]이기 때문이다. \(\S(M)\)의 두 원소의 곱은 곱셈처럼 \(xy\) 등과 같이 쓰는 것이 관례이다.
한편 quotient algebra의 universal property와 명제 2로부터 다음의 universal property 또한 자명하게 얻어진다.
명제 6 임의의 \(A\)-algebra \(E\)와 \(A\)-linear map \(u:M \rightarrow E\)가 다음 조건
\[u(x)u(y)=u(y)u(x)\qquad\text{for all $x,y\in M$}\]주어졌다 하자. 그럼 유일한 \(A\)-algebra homomorphism \(g: \S(M) \rightarrow E\)가 존재하여 \(f=g \circ\iota\)이도록 할 수 있다.
더 일반적으로, 임의의 \(A\)-module \(M,N\)과 자연수 \(n\geq 1\)를 고정하자. \(M^n\)에서 \(N\)로의 symmetric linear map은 다음 조건
\[f(x_{\sigma(1)},x_{\sigma(2)},\ldots, x_{\sigma(n)})=f(x_1,x_2,\ldots, x_n),\qquad \sigma\in S_n\]이 모든 \((x_i)\in M^n\)과 \(\sigma\in S_n\)에 대해 성립하는 것이다.
명제 7 두 \(A\)-module \(M,N\)에 대하여, 임의의 \(A\)-linear map \(g:\S^n(M) \rightarrow N\)에 대하여 다음의 식
\[(x_1,x_2,\ldots, x_n) \mapsto g(x_1x_2\cdots x_n)\]으로 정의되는 함수는 \(n\)-linear이고, 이 대응을 통해 \(\Hom_{\lMod{A}}(\S^n(M), N)\)에서, symmetric \(n\)-linear map \(M^n \rightarrow N\)들의 \(A\)-module로의 bijective \(A\)-module homomorphism이 정의된다.
이 때, \(A\)-module \(\S^n(M)\)을 \(M\)의 \(n\)번째 symmetric power\(n\)번째 대칭곱이라 부른다. 그럼 임의의 \(A\)-linear map \(u:M \rightarrow N\)에 대하여, \(\S^n(u): \S^n(M) \rightarrow \S^n(N)\)이 유도되며 이들의 direct sum을 취하면 \(\S(u)\)를 복원할 수 있다.
대칭대수의 성질들
앞서 functor \(T\)와 \(\rMod{A}\)의 연산들이 어떻게 행동하는지를 살펴보았다. 이제 이러한 결과들이 \(S\)에 대해서도 성립하는 것을 증명한다.
우선 \(M=\bigoplus_{i\in I} M_i\)가 \(A\)-module들 \(M_i\)들의 direct sum이라 하자. 그럼 우리는 다음의 isomorphism
\[\S(M)\cong \bigotimes_{i\in I} \S(M_i)\]를 얻는다. 이는 \(S\)가 forgetful functor \(U:\cAlg{A}\rightarrow \rMod{M}\)의 left adjoint이므로 colimit을 보존하고, \(\cAlg{A}\)에서의 colimit은 (\(\cRing\)에서의 coproduct가 tensor product이듯) \(\otimes_A\)로 주어지기 때문이다. 특히 명제 3과 같이 free \(A\)-module의 basis \((e_i)\)를 고정해두고 나면 다음의 명제를 얻는다.
명제 8 Free \(A\)-module \(M\)과 그 basis \((e_i)_{i\in I}\)에 대하여, \(\alpha:I \rightarrow \mathbb{N}\)을 finitely supported function이라 하자.
\[e^\alpha=\prod_{i\in I} e_i^{\alpha(i)}\]라 하면, 이러한 원소들을 모두 모아둔 것이 \(\S(M)\)의 basis가 된다.
이들의 multiplication은 \(e^\alpha e^\beta=e^{\alpha+\beta}\)로 주어진다. 즉 이 경우 \(\S(M)\)은 정확하게 polynomial algebra \(A[\x_i]_{i\in I}\)가 된다.
명제 4에 대응되는 결과는 다음의 명제이며, 그 증명 또한 동일하다.
명제 9 \(\S_{B}(B\otimes_AM)\rightarrow B\otimes_A\S_A(M)\)은 isomorphism이다.
외대수의 정의
정의 10 임의의 \(A\)-module \(M\)에 대하여, tensor algebra \(\T(M)\)의 two-sided ideal
\[\mathfrak{J}=\langle x\otimes x\mid x\in M\rangle\]을 생각하자. 그럼 quotient algbera \(\T(M)/\mathfrak{J}\)를 \(M\)의 exterior algebra외대수라 부르고 \(\bigwedge(M)\)으로 적는다.
\(\bigwedge(M)\)에서의 원소들의 곱셈은 \(\wedge\)로 적는 것이 관례이다. 한편 정의 5 이후의 논의와 마찬가지로, \(\mathfrak{J}\)는 homogeneous ideal이고 canonical inclusion \(\iota:M \hookrightarrow\bigwedge(M)\)이 존재한다는 것이 자명하다. 또, 명제 6과 마찬가지 이유에서 다음의 universal property가 성립한다.
명제 11 임의의 \(A\)-algebra \(E\)와 \(A\)-linear map \(u:M \rightarrow E\)가 다음 조건
\[u(x)^2=0\qquad\text{for all $x\in M$}\]주어졌다 하자. 그럼 유일한 \(A\)-algebra homomorphism \(g: \bigwedge(M) \rightarrow E\)가 존재하여 \(f=g \circ\iota\)이도록 할 수 있다.
명제 7과 비슷한 성질이 exterior algebra에서도 성립한다. 임의의 \(A\)-module \(M,N\)과 정수 \(n\geq 1\)에 대하여, \(f\)가 \(M^n\)에서 \(N\)로의 alternating linear map이라는 것은 다음 조건
\[f(x_{\sigma(1)},x_{\sigma(2)},\ldots, x_{\sigma(n)})=\epsilon(\sigma)f(x_1,x_2,\ldots, x_n),\qquad \sigma\in S_n\]이 모든 \((x_i)\in M^n\)과 \(\sigma\in S_n\)에 대해 성립하는 것이다. 이는 임의의 \(x_1,\ldots, x_{n-1}\)과 \(x\)에 대하여
\[f(x_1,\ldots, x_i, x,x,x_{i+1},\ldots, x_{n-1})=0\]이 성립하는 것과 동치이다.
명제 12 두 \(A\)-module \(M,N\)에 대하여, 임의의 \(A\)-linear map \(g:\S^n(M) \rightarrow N\)에 대하여 다음의 식
\[(x_1,x_2,\ldots, x_n) \mapsto g(x_1\wedge x_2\wedge\cdots\wedge x_n)\]으로 정의되는 함수는 \(n\)-linear이고, 이 대응을 통해 \(\Hom_{\lMod{A}}(\bigwedge^n(M), N)\)에서, symmetric \(n\)-linear map \(M^n \rightarrow N\)들의 \(A\)-module로의 bijective \(A\)-module homomorphism이 정의된다.
외대수의 성질들
마찬가지로 \(M=\bigoplus_{i\in I} M_i\)가 \(A\)-module들 \(M_i\)들의 direct sum이라 하였을 때, \(\bigwedge\)가 left adjoint인 것으로부터 \(\bigwedge(M)\)이 \(\bigwedge(M_i)\)들의 colimit이 되어야 한다는 것을 안다. 이를 엄밀히 하기 위해서는 alternating algebra들의 category에서의 colimit을 정의해야 한다. 이는 \(\cAlg{A}\)와 유사하게 tensor product로 나오지만, Koszul sign convention이 붙어있다. 이는 별다른 것은 아니고, 정의로부터 exterior algbebra의 degree \(m,n\)의 원소를 곱하면 \((-1)^{mn}\)의 부호가 생기게 되므로 이를 반영해주는 것이다. 당장은 이를 엄밀하게 쓸 이유는 없으니 다음 명제만 소개한다.
명제 13 Free \(A\)-module \(M\)과 그 basis \((e_i)_{i\in I}\)에 대하여, \(I\)의 total ordering을 하나 고정하자. 임의의 유한한 부분집합 \(J\subseteq I\)에 대하여
\[e_J=e_{j_1}\wedge e_{j_2}\wedge\cdots\wedge e_{j_k},\qquad j_1<\cdots < j_k, \quad J=\{j_1,\ldots, j_k\}\]라 하면, 이러한 \(e_J\)들을 모아둔 것이 \(\bigwedge (M)\)의 basis가 된다.
예를 들어, \(e_1\wedge e_2\wedge e_3\)과 \(e_1\wedge e_3\wedge e_2\)는 나중 두 원소의 위치를 서로 바꾸어 주기만 하면 부호의 차이만 제외하고는 같은 원소가 되므로 위와 같이 \(I\)에 아무렇게나 order를 준 후 이에 맞추어 배열하는 식으로 무의미한 중복을 피할 수 있다. 다음 명제는 더더욱 설명할 것이 없다.
명제 14 \(\bigwedge_{B}(B\otimes_AM)\rightarrow B\otimes_A\bigwedge_A(M)\)은 isomorphism이다.
참고문헌
[Bou] Bourbaki, N. Algebra I. Elements of Mathematics. Springer. 1998.
-
Category \(\Ring\)에서의 coproduct는 free product와 비슷한 식으로 정의되었던 것을 기억하자. (§환의 곱, 쌍대곱, 텐서곱, ⁋명제 3) 반면, 같은 글에서 우리는 category \(\cRing\)의 coproduct는 tensor product \(\otimes\)로 주어진다는 것 또한 확인하였다. ↩

댓글남기기