Retraction과 section

앞선 글의 말미는 단사함수와 전사함수의 새로운 정의를 내릴 수 있도록 해 준다. (§함수들 사이의 연산, ⁋참고)

명제 1 함수 \(f:A\rightarrow B\)를 생각하자. 만일 어떠한 \(r:B\rightarrow A\)가 존재하여 \(r\circ f=\id_A\)라면 \(f\)는 단사함수다. 또 어떠한 \(s:B\rightarrow A\)가 존재하여 \(f\circ s=\id_B\)라면 \(f\)는 전사함수다.

반대로, 만일 \(f\)가 전사함수라면 어떤 \(s:B\rightarrow A\)가 존재하여 \(f\circ s=\id_B\)이고, 만일 \(f\)가 단사함수라면 어떤 \(r:B\rightarrow A\)가 존재하여 \(r\circ f=\id_A\)이다.

증명

두 번째 부분은 이미 이전 글에서 보였다. 따라서 처음 부분만 보이면 된다. 우선 \(r\circ f=\id_A\)라 하자. 만일 \(f(x)=f(y)\)라면

\[x=\id_{A}(x)=(r\circ f)(x)=r\circ(f(x))=r\circ(f(y))=(r\circ f)(y)=\id_{A}(y)=y\]

이므로 \(f\)는 단사함수이다. 이와 비슷하게, 만일 \(f\circ s=\id_{B}\)라면 임의의 \(y\in B\)에 대하여

\[y=\id_{B}(y)=(f\circ s)(y)=f(s(y))\]

이므로 \(y\in f(A)\)이고, 따라서 \(f\)는 전사함수이다.

따라서 함수 \(f:A\rightarrow B\)가 단사함수라는 것은 다음의 diagram

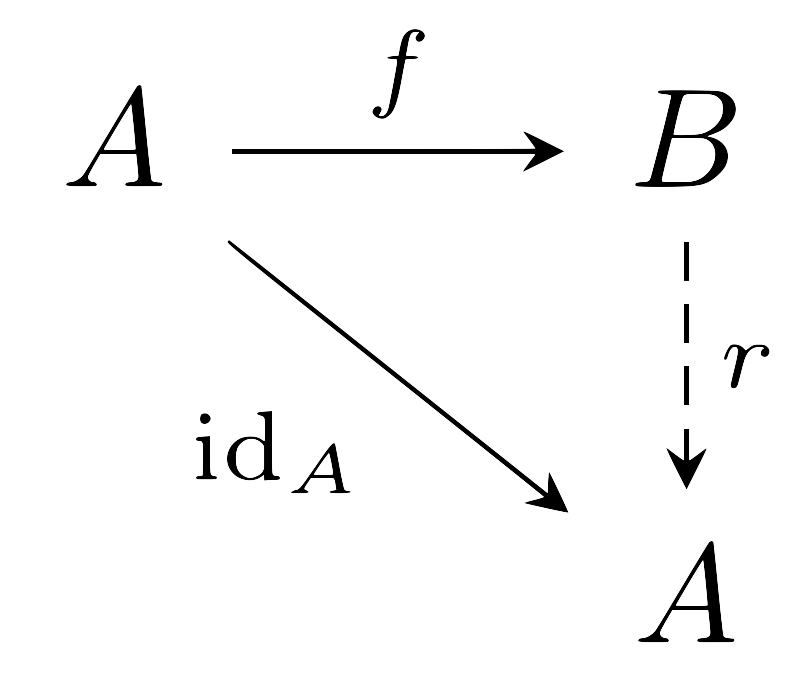
이 commute하도록 하는 \(r:B\rightarrow A\)가 있다는 것과 같은 말이고, \(f:A\rightarrow B\)가 전사함수라는 것은 다음의 diagram

이 commute하도록 하는 \(s:B\rightarrow A\)가 있다는 것과 같은 말이다. 이러한 성질을 만족하는 \(r,s\)에도 이름이 있다.

정의 2 \(f\)가 \(A\)에서 \(B\)로의 단사함수라 하자. 그럼 \(r\circ f=\id_A\)를 만족하는 함수 \(r:B\rightarrow A\)를 \(f\)의 retraction_수축이라 한다.
만일 \(f\)가 \(A\)에서 \(B\)로의 전사함수라면, \(f\circ s=\id_B\)를 만족하는 함수 \(s:B\rightarrow A\)를 \(f\)의 section_단면이라 부른다.

만일 \(f\)가 단사함수이고 \(r\)이 retraction이라면 \(f\)를 \(r\)의 section으로 볼 수 있고, 반대로 \(f\)가 전사함수이고 \(s\)가 section이라면 \(f\)를 \(s\)의 retraction으로 볼 수도 있다. 따라서 retraction은 전사이고 section은 단사이다.

한편, 함수 \(f:A \rightarrow B\)와 \(X\subseteq A, Y\subseteq B\)에 대하여 항상 다음의 두 식

\[X\subseteq f^{-1}(f(X)),\qquad f(f^{-1}(Y))\subseteq Y\]

가 성립하며 그 증명 또한 자명하다. 만일 \(f\)가 단사라면, §함수들 사이의 연산, ⁋참고와 같이 정의된 \(r\)에 대하여

\[f^{-1}(f(X))=r(f(X))=\id_A(X)=X\]

이고, 만일 \(f\)가 전사라면 마찬가지로 §함수들 사이의 연산, ⁋참고와 같이 정의된 \(s\)에 대하여

\[Y=\id_B(Y)=f(s(Y))\subseteq f(f^{-1}(Y))\]

이므로 위의 식들은 등호가 된다. 다음 명제의 증명은 모두 자명하지만, 결과는 기억할 필요가 있다.

명제 3 두 함수 \(f:A\rightarrow B\)와 \(f':B\rightarrow C\)에 대하여, \(f''=f'\circ f\)라 하자.

1. 만일 \(f\)와 \(f'\)가 모두 단사함수라면 \(f''\) 또한 마찬가지이다.
   이 때 \(r\)과 \(r'\)을 \(f\)와 \(f'\) 각각의 retraction이라 하면, \(r\circ r'\)이 \(f''\)의 retraction이 된다.
2. 만일 \(f\)와 \(f'\)가 모두 전사함수라면, \(f''\) 또한 마찬가지이다.
   이 때 \(s\)와 \(s'\)를 \(f\)와 \(f'\) 각각의 section이라 하면, \(s\circ s'\)는 \(f''\)의 section이 된다.
3. \(f''\)가 단사함수라면 \(f\) 또한 단사함수다.
   특히 \(r''\)이 \(f''\)의 retraction이라면, \(r''\circ f'\)이 \(f\)의 retraction이다.
4. 만일 \(f''\)가 전사함수라면 \(f'\) 또한 전사함수다.
   특히 \(s''\)이 \(f''\)의 section이라면, \(f\circ s''\)이 \(f'\)의 section이다.

증명

1. 우선 \(f''(a_1)=f''(a_2)\)라 하자. 그럼 \(f'(f(a_1))=f'(f(a_2))\)이므로, \(f'\)와 \(f\)가 단사라는 사실을 순서대로 써 주면 \(a_1=a_2\)를 얻는다. 즉 \(f''\)은 단사함수이다.
   이제 \(r\), \(r'\)을 각각 \(f\), \(f'\)의 retraction이라 하자. 즉 \(r\circ f=\id_A\)이고 \(r'\circ f'=\id_B\)이다. 그럼 임의의 \(a\in A\)에 대하여,

   \[((r\circ r')\circ(f'\circ f))(a)=(r\circ\id_{B}\circ f)(a)=(r\circ f)(a)=\id_{A}(a)=a\]

   이므로 \(r\circ r'\)는 \(f''\)의 retraction이다.

2. \(c\in C\)라 하자. 그럼 \(f'\)가 전사이므로 \(f'(b)=c\)이도록 하는 \(b\in B\)가 존재한다. 이제 다시 \(f\)가 전사이므로 \(f(a)=b\)이도록 하는 \(a\in A\)가 존재한다. 따라서 \(f''(a)=c\)이고 \(f''\)는 전사함수이다. 이제 \(s\)와 \(s'\)를 \(f\)와 \(f'\) 각각의 section이라 하면, 임의의 \(c\in C\)에 대하여

   \[((f'\circ f)\circ(s\circ s'))(c)=(f'\circ\id_{B}\circ s')(c)=(f'\circ s')(c)=\id_{C}(c)=c\]

   이므로 \(s\circ s'\)는 \(f''\)의 section이다.

3. 어떠한 \(a_1\), \(a_2\in A\)에 대하여 \(f(a_1)=f(a_2)\)라 하자. 그럼 \(f''(a_1)=f'(f(a_1))=f'(f(a_2))=f''(a_2)\)이고, \(f''\)가 단사함수이므로 \(a_1=a_2\)이다. 따라서 \(f\)도 단사함수다. 이제 임의의 \(a\in A\)에 대하여,

   \[((r''\circ f')\circ f)(a)=(r''\circ f'')(a)=\id_A(a)=a\]

   이므로 \(r''\circ f'\)는 \(f\)의 retraction이다.

4. \(f''\)가 전사함수이므로, 어떠한 \(c\in C\)에 대하여 \(f''(a)=c\)인 \(a\in A\)가 존재한다. 따라서 \(f'(f(a))=c\)이므로, \(f(a)=b\in B\)가 \(f'(b)=c\)를 만족한다. 또 임의의 \(c\in C\)에 대하여

   \[(f'\circ(f\circ s''))(c)=(f''\circ s'')(c)=\id_C(c)=c.\]

명제 4

1. \(A,B,C\)가 집합이라 하고, 전사함수 \(g:A\rightarrow B\)와 함수 \(f:A\rightarrow C\)를 생각하자. 그럼 $f=h\circ g$를 만족하는 $h:B\rightarrow C$가 존재하는 것은 $(g(x)=g(y))\implies(f(x)=f(y))$가 성립하는 것과 동치이다.
   만약 이 조건들이 만족되면, \(f=h\circ g\)를 만족하는 \(h\)는 \(h\)는 \(f\)에 의해 유일하게 결정되며, 만일 \(s\)가 \(g\)의 section이라면 \(h=f\circ s\)이다.
2. \(A,B,C\)가 집합이고, 단사함수 \(g:A\rightarrow B\)와 함수 \(f:C\rightarrow B\)를 생각하자. 그럼 어떤 함수 $h:C\rightarrow A$가 존재하여 $f=g\circ h$인 것은 $f(C)\subseteq g(A)$인 것과 동치이다.
   만약 이 조건들이 만족되면 \(h\)는 \(f\)에 의해 유일하게 결정되며, 만일 \(r\)이 \(g\)의 retraction이라면 \(h=r\circ f\)이다.

1번의 결과는 다음의 diagram

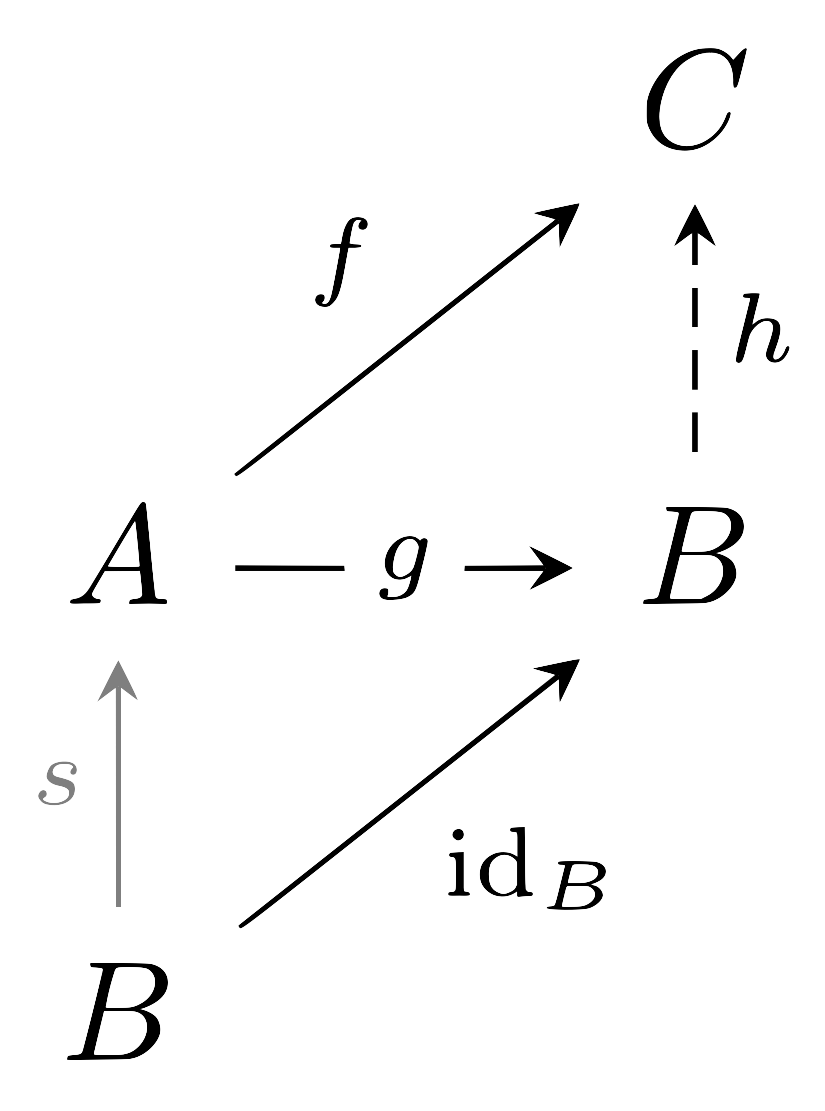
이 commute하도록 하는 \(h\)가 존재한다는 것이고, 2번의 경우는 다음과 같은 diagram

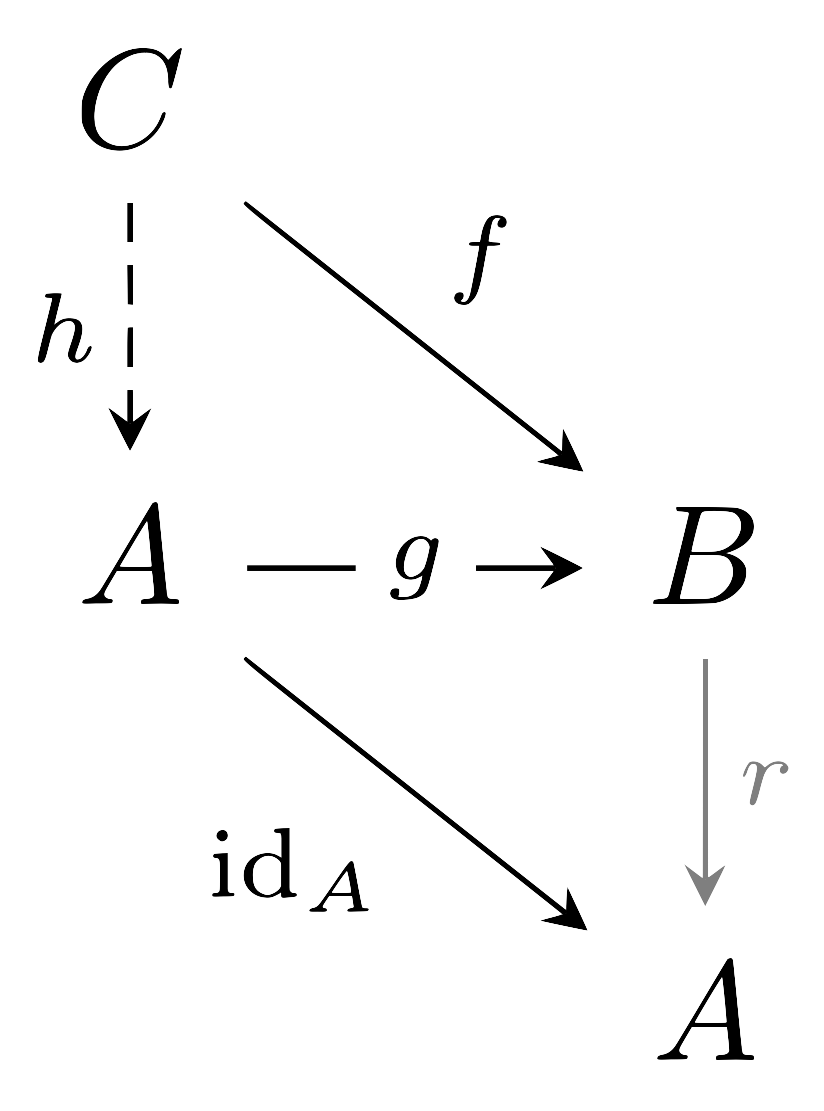
이 commute하도록 하는 \(h\)가 존재한다는 것이다.

명제 4의 증명

1. 우선 \(f=h\circ g\)라 하자. 만일 \(g(x)=g(y)\)라면

   \[f(x)=(h\circ g)(x)=h(g(x))=h(g(y))=(h\circ g)(y)=f(y)\]

   이므로 \((g(x)=g(y))\implies(f(x)=f(y))\)가 성립한다. 우리는 이 명제의 반대방향을 보여서 이 두 조건들이 동치임을 보여야 하고, 또 이 동치인 두 조건이 만족되면 \(h\)가 \(h=f\circ s\)로 유일하게 결정됨을 보여야 한다.
   우선 이 조건들이 만족되면 \(h\)는 유일할 수밖에 없다는 것을 먼저 관찰하자.
   \(h\)는 \(B\)에서의 각각의 원소 \(y\)들의 함숫값에 의해 결정되는데, \(g\)가 전사함수이므로 \(g\)의 어떤 section \(s\)에 대하여 \(s(y)=x\)이도록 할 수 있다. 이제

   \[h(y)=(f\circ s)(y)=f(x)\]

   이다. 또 다른 section \(s'\)가 존재하여 \(s'(y)=x'\)라 하더라도,

   \[g(x)=g(s(y))=y=g(s'(y))=g(x')\]

   이므로 동치인 조건 중 나중의 조건에 의하여 \(f(x)=f(x')\)이고, 따라서 \(h(y)\)의 값은 \(s\)의 선택에 관계없이 동일하다. 즉, \(h\)는 존재한다면 유일하다.

   이제 주어진 동치관계의 반대방향을 증명해야 한다. \((g(x)=g(y))\implies(f(x)=f(y))\)를 가정하자. \(s\)를 \(g\)의 section이라 하고, 유일성 증명에서 힌트를 얻어 \(h=f\circ s\)로 정의하자. 그럼 임의의 \(x\in A\)에 대하여

   \[(h\circ g)(x)=((f\circ s)\circ g)(x)=f(s(g(x)))\]

   이 성립한다. 한편

   \[g(s(g(x)))=\id_B(g(x))=g(x)\]

   이므로, 주어진 조건에 의해 \(f(s(g(x)))=f(x)\)이다. 즉 \(h(g(x))=f(x)\)이므로 주어진 조건을 만족하는 \(h\)가 존재한다.

2. 우선 \(f=g\circ h\)라 하자. 그럼 임의의 \(y\in f(C)\)에 대하여 \(y=f(x)\)라 하면 \(y=f(x)=g(h(x))\in g(A)\) 이므로 \(f(C)\subseteq g(A)\)임은 자명하다. 1의 증명과 마찬가지로, 먼저 \(h\)의 유일성을 보이자. \(h\)는 \(f=g\circ h\)를 만족하는 함수로 정의되므로, \(h\)가 임의의 \(y\in G\)에 대하여 유일한 함숫값을 가짐을 보이기 위해서는 다음의 식

   \[h(y)=(\id_A\circ h)(y)=((r\circ g)\circ h)(y)=(r \circ f)(y)\]

   의 우변이 retraction \(r\)의 선택에 관계없이 동일한 값을 가짐을 보이면 된다. 그런데 \(r\circ g=r'\circ g=\id_A\)이므로, 임의의 \(g(x)\in g(A)\)에 대하여 \(r(g(x))=x=r'(g(x))\)이다. 즉, \(r\vert_{g(A)}=r'\vert_{g(A)}\)이다. 이제 동치인 조건 중 나중의 조건에 의하여 \(r\)과 \(r'\)은 \(f(y)\in f(C)\subseteq g(A)\) 위에서 같은 값을 가져야 한다. 따라서 \(h\)는 존재한다면 유일하다.

   이제 반대방향을 보여야 한다. 유일성 증명에서 힌트를 얻어 \(h=r\circ f\)로 정의하자. 만일 \(f(C)\subseteq g(A)\)라면, 임의의 \(x\in C\)에 대하여

   \[(g\circ h)(x)=(g\circ(r\circ f))(x)=(g\circ r)(f(x))\]

   이 성립한다. 그런데 \(f(x)\in f(C)\subseteq g(A)\)이므로, \(f(x)=g(y)\)라 하면

   \[(g\circ r)(f(x))=(g\circ r)(g(y))=(g\circ(r\circ g))(y)=(g\circ\id_A)(y)=g(y)=f(x)\]

   이므로 \((g\circ h)(x)=f(x)\)가 모든 \(x\in C\)에 대해 성립한다. 즉 주어진 조건을 만족하는 \(h\)가 존재한다.

---

참고문헌

[Bou] N. Bourbaki, Theory of Sets. Elements of mathematics. Springer Berlin-Heidelberg, 2013.

---