우리는 앞선 글들에서 이항관계를 정의했다. 이 정의에 따르면, 자연수 집합 $\mathbb{N}$에서 정의된 이항관계 $<$는 다음의 집합
\[{<}=\{(0,1),(0,2),\ldots, (1,2),(1,3),\ldots, \}\]을 의미한다.

이제 §이항관계, ⁋정의 7의 표기를 따르면 ${<}(1)$은 $(1,n)\in\mathbb{N}$이도록 하는 모든 $n\in\mathbb{N}$들의 모임이고 따라서
\[{<}(1)=\{2,3,\ldots\}\]이 된다. 거꾸로 모든 자연수 $k$에 대하여 집합 ${<}(k)$에 대한 정보가 주어진다면 집합 $<$를 복원할 수도 있다.
위의 논의는 일반적인 이항관계 $(R,A,B)$에 대하여도 성립하며, 따라서 임의의 이항관계 $R$이 주어진다는 것은 정확하게 각각의 $a\in A$에 대하여, 집합 $R(a)$를 대응시키는 규칙이 주어진 것으로 생각할 수 있다. 이러한 측면에서 함수란 모든 $a\in A$에 대하여 $R(a)$가 한원소집합인 이항관계라고 생각할 수 있다.
함수의 정의
정의 1 공집합이 아닌 집합 $A$에 대하여, 이항관계 $f=(F,A,B)$가 함수function라는 것은 $A=\pr_1F$이고 각각의 $x\in A$에 대하여 $F(\{x\})$가 한원소집합1인 것이다.
조건 $A=\pr_1F$는 $A$의 모든 원소 $x$가
모든 $x\in A$에 대하여,
유일한 $y\in B$가 존재하여 $(x,y)\in F$
인 것이다. 이 때의 $y$를 $f$의 $x$에서의 함숫값이라 부르고, 이 때 집합 $F(\{x\})$의 유일한 원소를 $f(x)$로 표기한다. 또, 집합 $A=\pr_1F$를 $f$의 정의역domain이라 부른다.
위의 표기를 따라, 이항관계 $F$에 대한 집합 $X\subseteq A$의 image는 $F(X)$ 대신 $f(X)$로, 집합 $Y\subseteq B$의 preimage도 $F^{-1}(Y)$ 대신 $f^{-1}(Y)$로 적는다. (§이항관계, ⁋정의 5와 §이항관계들 사이의 연산, ⁋정의 1) 또, triple $f=(F,A,B)$는 간단히 $f:A\rightarrow B$과 같이 적는다.
한편, 함수 $f=(F,A,B)$를 나타내는 집합
\[F=\{(x,y)\mid (y=f(x))\wedge(x\in A)\}\]는 “좌표평면” $A\times B$ 위에 그려진
특수한 경우에는 함숫값을 나타내기 위해 $f_x$ 등과 같은 표현도 사용한다. 이러한 표기법을 사용할 때에는 특별히 $f$의 정의역을 index set첨수집합이라 부르고, 이 때 $F$를 family라 부른다. $f=(F,I,A)$를 family로 생각할 때에는 $F$를 나타낼 때 $(f_i)_{i\in I}$와 같이 표기한다.
만일 $f$가 어떠한 집합 $A$에서 $A$로의 함수라면, $x\in A$가 $f$에 의해 고정된다는 것은 $f(x)=x$인 것이다.
정의 2 임의의 집합 $A$에 대하여, 항등함수 $\id_A$를 triple $(\Delta_A,A,A)$으로 정의한다. 즉, $\id_A$는 임의의 $x\in A$에 대하여, 식 $f(x)=x$로 정의되는 함수이다.
정의에 의하여, $\id_A$는 $A$의 모든 원소를 고정하는 함수이다.
Commutative diagram
한번에 많은 수의 함수들을 다룰 때에는 다음과 같은 diagram들을 사용하는 것이 편하다.

여기서 $A\overset{f}{\longrightarrow}B$는 $f:A\rightarrow B$의 간편한 표기이다.
위와 같은 상황에서 만일 임의의 $x\in B$에 대하여 $(i\circ g)(x)=(j\circ h)(x)$가 성립한다면, 다음의 사각형

이 commute가환한다고 말한다. 이와 유사하게 다음의 diagram
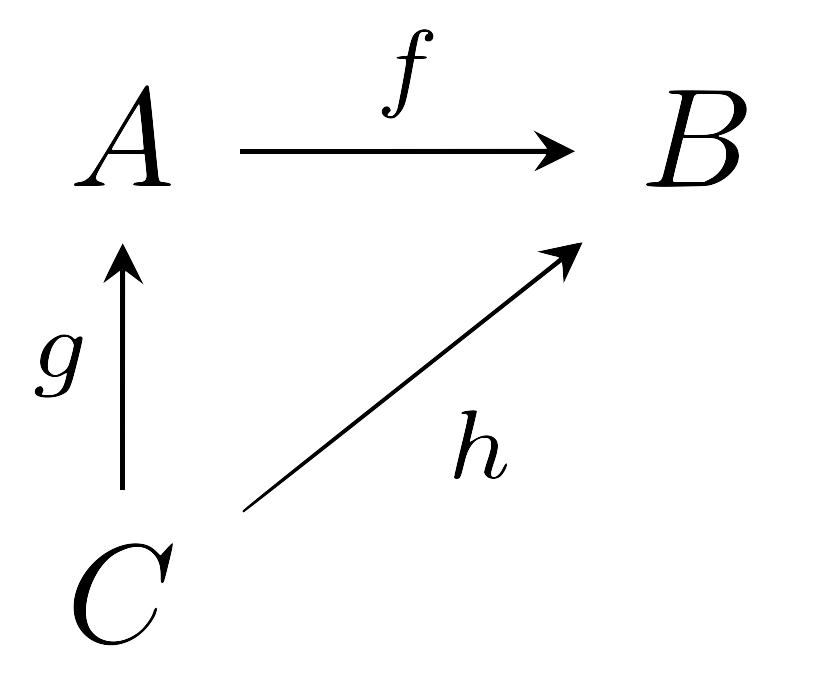
이 commutative diagram가환그림이라는 것은 $h(x)=(f\circ g)(x)$가 모든 $x$에 대해 성립함을 의미한다. 이 상황을 간략하게 $h=f\circ g$라고 표현하기도 하는데, 이 표기는 $H=F\circ G$가 성립한다는 것 뿐만 아니라 양변의 source와 target 또한 모두 일치한다는 것을 내포한다.
한편 diagram을 다룰 때, 화살표를 통해 명시적으로 표현되지 않았더라도 각각의 대상 $A$마다 $A$에서 $A$로의 함수 $\id_A$가 그려져 있는 것으로 생각한다. 따라서 위의 삼각형이 commute한다는 것은 엄밀하게 이야기하자면 $h=f\circ g$ 뿐만 아니라
\[{\id_B}\circ h=f\circ g,\qquad h\circ{\id_C}=f\circ{\id_A}\circ g,\quad\cdots\]를 모두 포함하는 것이다. 그러나 §이항관계들 사이의 연산, ⁋정의 9에서 살펴본 항등함수의 성질에 의해 위의 식들은 모두 $h=f\circ g$와 다를 것이 없다. 반면

가 commute한다는 것은 다음의 세 조건
\[{\id_A}=g\circ h\circ f,\quad {\id_B}=f\circ g\circ h,\quad {\id_C}=h\circ f\circ g\]이 모두 성립하는 것이다. 특별히 다음의 diagram

이 commute한다는 것은 $g\circ f=\id_A$이고 $f\circ g=\id_B$이라는 것이다.
함수의 확장과 제한
정의 3 두 함수 $f=(F,A,B),f’=(F’,A’,B’)$가 집합 $S$에서 compatible하다는 것은 $S$가 $f$와 $f’$의 정의역에 각각 포함되어 있고, 모든 $x\in S$에 대하여 $f(x)=f’(x)$인 것이다.
두 함수 $f$와 $f’$가 주어졌고, $S=\pr_1 F\cap\pr_1 F’$가 공집합이 아니라 하자. $S$에서 두 함수가 compatible하다면 $\pr_1F\cup\pr_1F’$를 정의역으로 갖는 새로운 함수 $g$를 다음의 식
\[g(x)=\begin{cases}f(x)&x\in \pr_1F\setminus\pr_1F'\\ f(x)=f'(x)&x\in \pr_1F\cap\pr_1F'\\ f'(x)&x\in\pr_1F'\setminus\pr_1F\end{cases}\]으로 정의할 수 있다. 이러한 상황을 다음과 같이 정의한다.
정의 4 두 함수 $f=(F,A,B)$, $f’=(F’,A’,B’)$가 주어졌다 하자. 만일 $F\subseteq F’$이고 $B\subseteq B’$라면 $f’$를 $f$의 extension확장이라 부르고, $f’$가 $f$를 확장한다고 말한다.
이와 반대로 어떠한 함수를 더 작은 정의역으로 제한시킬 수도 있다. $f=(F,A,B)$가 함수이고 $X\subseteq A$라 하자. 관계 $R$을
$(x\mathrel{R} y)$ if and only if $((x\in X)\wedge(y=f(x)))$
로 정의한다면, 이를 만족하는 $(x,y)$들을 모아둔 $R$은 함수가 되며, 이 함수의 정의역은 $X$가 된다. 따라서 다음과 같이 새로운 함수를 정의할 수 있다.
정의 5 위와 같이 정의된 함수 $g$를 $f$의 $A$ 위로의 restriction제한이라 부르며, 이를 $f|_{X}$와 같이 적는다.
참고문헌
[Bou] N. Bourbaki, Theory of Sets. Elements of mathematics. Springer Berlin-Heidelberg, 2013.
-
엄밀히 이야기하자면 집합의 크기를 아직 정의하지 않았지만, 이 조건은 $x,y\in R(a)\implies x=y$ 등으로 표현할 수 있다. ↩

댓글남기기