부분곱과 결합법칙
집합의 곱이 결합법칙을 만족한다는 이야기를 하기 위해서는 우선 부분곱을 정의해야 한다.
정의 1 Family \((A_i)_{i\in I}\)와 그 product \(\prod_{i\in I} A_i\)가 주어졌다고 하자. 그럼 index set의 부분집합 \(J\subseteq I\)에 대하여, \(\prod_{j\in J} A_j\)를 부분곱partial product이라 부른다.
\(\prod_{i\in I}A_i\)의 부분곱 \(\prod_{j\in J}A_j\)가 주어졌다 하자. 그럼 임의의 \(F\in\prod_{i\in I}A_i\)에 대하여,
\[f\circ\id_J=\biggl(F\circ\Delta_J, J, \bigcup_{j\in J} A_j\biggr)\]은 새로운 함수이며, 각각의 \(j\)에 대하여 \((f\circ\id_J)(j)=f(j)\in A_j\)를 만족한다. 즉 \(F\circ\Delta_J\)는 \(\prod_{j\in J}A_j\)의 원소이다.
위의 문단에 의하여, \(F\mapsto F\circ\Delta_J\)는 \(\prod_{i\in I}A_i\)에서 \(\prod_{j\in J}A_j\)로의 함수를 정의한다. 이를 성분함수의 표기를 빌려 \(\pr_J\)로 적는다. 그럼 \(K\subseteq J\subseteq I\)에 대하여, 곱집합 \(\prod_{i\in I}A_i\)에서 부분곱 \(\prod_{j\in J}A_j\)로의 \(J\)번째 성분함수와, 곱집합 \(\prod_{j\in J}A_j\)에서 이 곱집합의 부분곱 \(\prod_{k\in K}A_k\)로의 \(K\)번째 성분함수
\[\prod_{i\in I}A_i\longrightarrow \prod_{j\in J}A_j\longrightarrow \prod_{k\in K}A_k\]의 합성은 간단히 곱집합 \(\prod_{i\in I}A_i\)에서 이 곱집합의 부분곱 \(\prod_{k\in K}A_k\)로의 \(K\)번째 성분함수 \(\pr_K\)와 같다. \(\Delta_K=\Delta_J\circ\Delta_K\)이기 때문이다.
명제 2 모든 성분들이 공집합이 아닌 family \((A_i)_{i\in I}\)를 생각하고, \(J\subseteq I\)라 하자. 만일 \(g:J\rightarrow\bigcup_{i\in I} A_i\)가 \(g(j)\in A_j\)를 만족한다면, \(g\)의 extension \(f:I\rightarrow\bigcup_{i\in I} A_i\)가 존재하여 \(f(i)\in A_i\)가 성립한다.
증명
\(g=(G,J,\bigcup A_i)\)라 하자. 각각의 \(i\in I\setminus J\)에 대하여, \(A_i\)가 공집합이 아니므로 \(x_i\in A_i\)를 하나씩 뽑을 수 있다. 이제
\[F=G\cup\biggl(\bigcup_{i\in I\setminus J}\{(i, x_i)\}\biggr)\]으로 정의하고 \(f=(F,I,\bigcup A_i)\)라 하면 원하는 결과를 얻는다.
명제 3 공집합이 아닌 index set \(I\)를 갖는 family \((A_i)_{i\in I}\)가 \(I\neq\emptyset\)가 주어졌다 하자. 만일 \((J_k)_{k\in K}\)이 \(I\)의 분할이라면, \(\prod_{i\in I}A_i\)에서 \(\prod_{k\in K}\left(\prod_{j\in J_k}A_j\right)\)로의 함수 \(f\mapsto (\pr_{J_k}(f))_{k\in K}\) 또한 전단사함수이다.
증명 1
\((J_k)_{k\in K}\)이 분할이므로, \(f_k:J_k\rightarrow \bigcup_{i\in I} A_i\)는 쌍마다 서로소인 정의역을 갖는 함수들의 family이고, 따라서 §집합의 합, ⁋명제 2를 적용하면 전단사함수를 얻는다.
위의 증명도 간결하지만, universal property를 이용하는 다음의 증명 또한 아름답다.
증명 2
표기법 상의 깔끔함을 위해 일괄적으로
-
Index set \(K\)에 대한 곱집합 \(\prod_{k\in K}\left(\prod_{j\in J_k}A_j\right)\)의 \(k\)번째 성분함수
\[\prod_{k\in K}\left(\prod_{j\in J_k}A_j\right)\rightarrow\prod_{j\in J_k}A_j\]을 \(\pr_k\),
-
Index set \(J_k\)에 대한 곱집합 \(\prod_{j\in J_k}A_j\)의 \(j\)번째 성분함수
\[\prod_{j\in J_k}A_j\rightarrow A_j\]도 \(\pr_j\),
-
Index set \(I\)에 대한 곱집합 \(\prod_{i\in I}A_i\)의 \(i\)번째 성분함수
\[\prod_{i\in I}A_i\rightarrow A_i\]도 \(\pr_i\)
으로 표기하자. 글자로 보았을 때는 약간의 혼동이 있을 수 있지만, diagram 상에서는 source와 target이 모두 명시되므로 혼동의 여지가 없다.
\((J_k)_{k\in K}\)는 \(I\)의 분할이므로, 각각의 \(i\in I\)마다 유일한 \(k\in K\)가 존재하여 \(i\in J_k\)이다. 이제 함수 \(\pr_{ik}\)를 다음의 합성
\[\pr_{ik}:\prod_{k\in K}\left(\prod_{j\in J_k}A_j\right)\overset{\pr_k}{\longrightarrow}\prod_{j\in J_k}A_j\overset{\pr_i}{\longrightarrow}A_i\]으로 정의하자. 그럼 곱집합 \(\prod_{i\in I}A_i\)의 universal property로부터, 다음의 diagram을 commute하도록 하는 \(\phi:\prod_{k\in K}\left(\prod_{j\in J_k}A_j\right)\rightarrow\prod_{i\in I}A_i\)가 존재함을 안다.
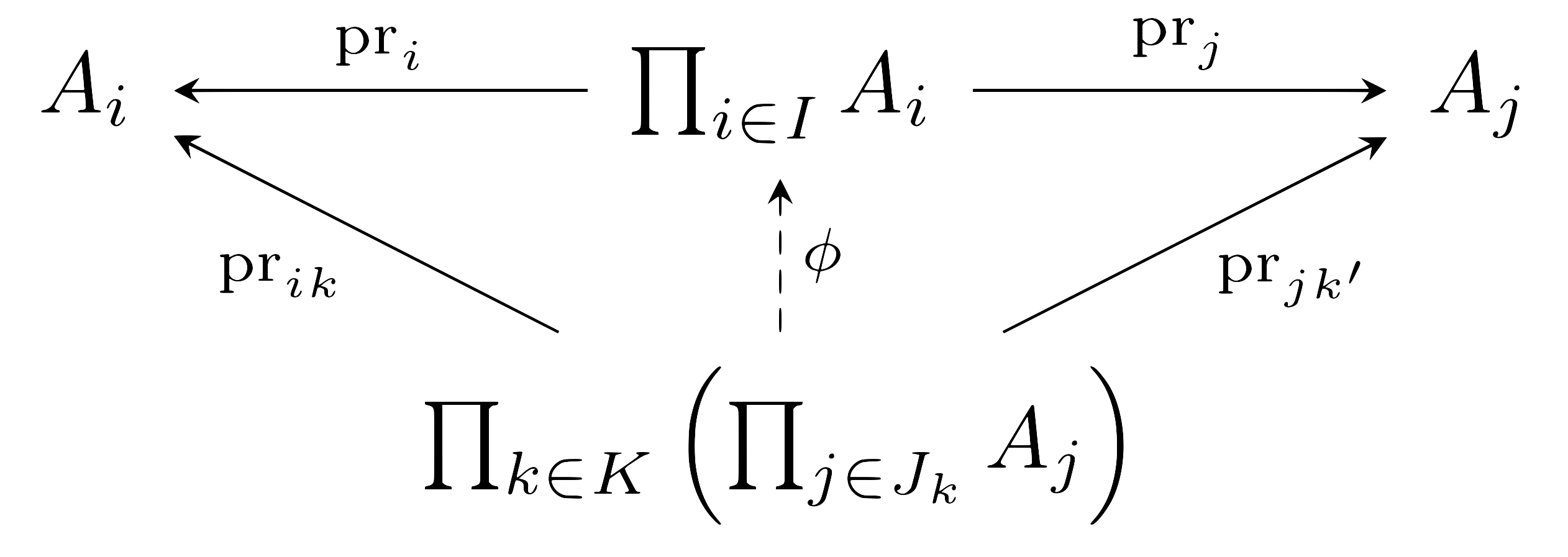
비슷하게 index set \(K\)에 대한 곱집합 \(\prod_{k\in K}\left(\prod_{j\in J_k}A_j\right)\)의 universal property로부터, 다음의 diagram을 commute하게 하는 \(\psi:\prod_{i\in I}A_i\rightarrow\prod_{k\in K}\left(\prod_{j\in J_k}A_j\right)\)가 존재함을 안다.
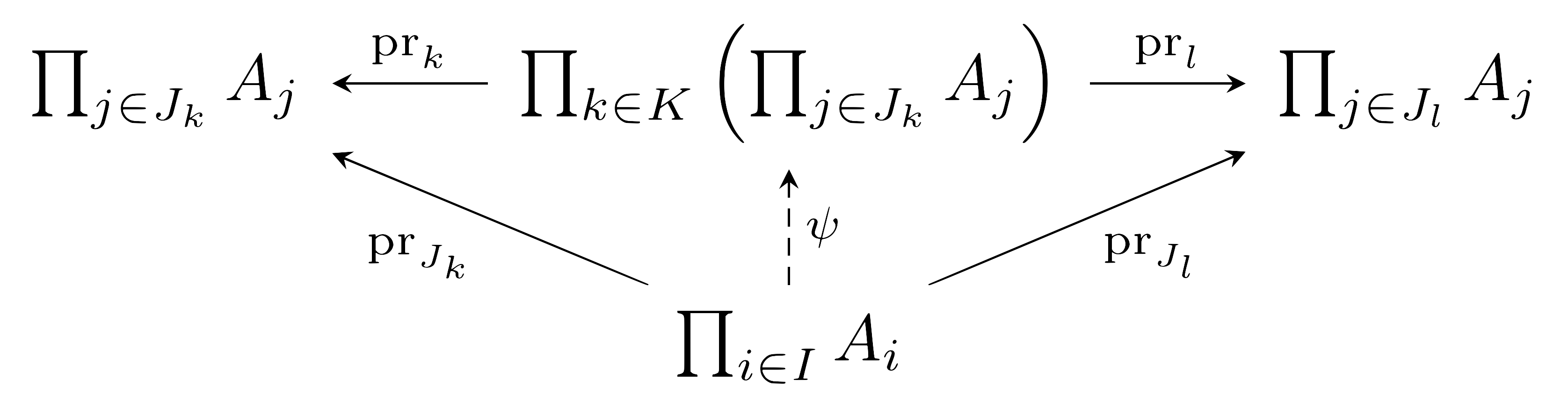
그럼 \(\phi\circ\psi\)와 \(\psi\circ\phi\)가 각각 항등함수이고, 따라서 이들이 원하는 전단사함수가 된다.
예를 들어 \(\phi\circ\psi\)가 \(\prod_{i\in I}A_i\)에서 자기자신으로의 항등함수임을 보이자. 이를 위해서는 모든 \(i\in I\)에 대하여 다음의 diagram이 commute함을 보이면 충분하다.
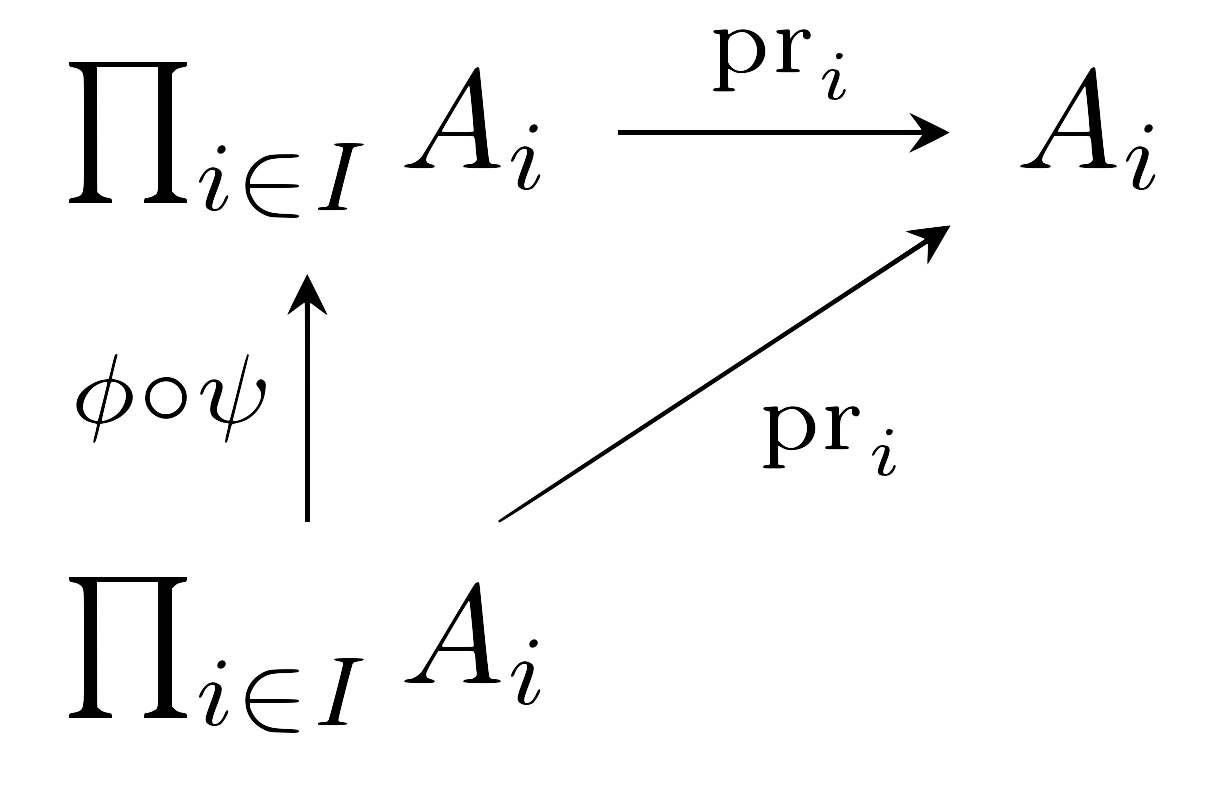
곱집합의 universal property는 위의 diagram을 commute하게 하는
이제
\[{\pr_i}\circ(\phi\circ\psi)=({\pr_i}\circ\phi)\circ\psi={\pr_{ik}}\circ\psi={\pr_i}\circ({\pr_k}\circ\psi)={\pr_j}\circ{\pr_{J_k}}=\pr_j\]에서 원하는 결론을 얻는다. (마지막 등식은 \(\pr_j\)를 \(\{j\}\subseteq I\)로의 성분함수로 보았다.) 이 식은 복잡해보이지만, 그냥 다음의 diagram이 commute한다는 것을 식으로 쓴 것에 불과하다.
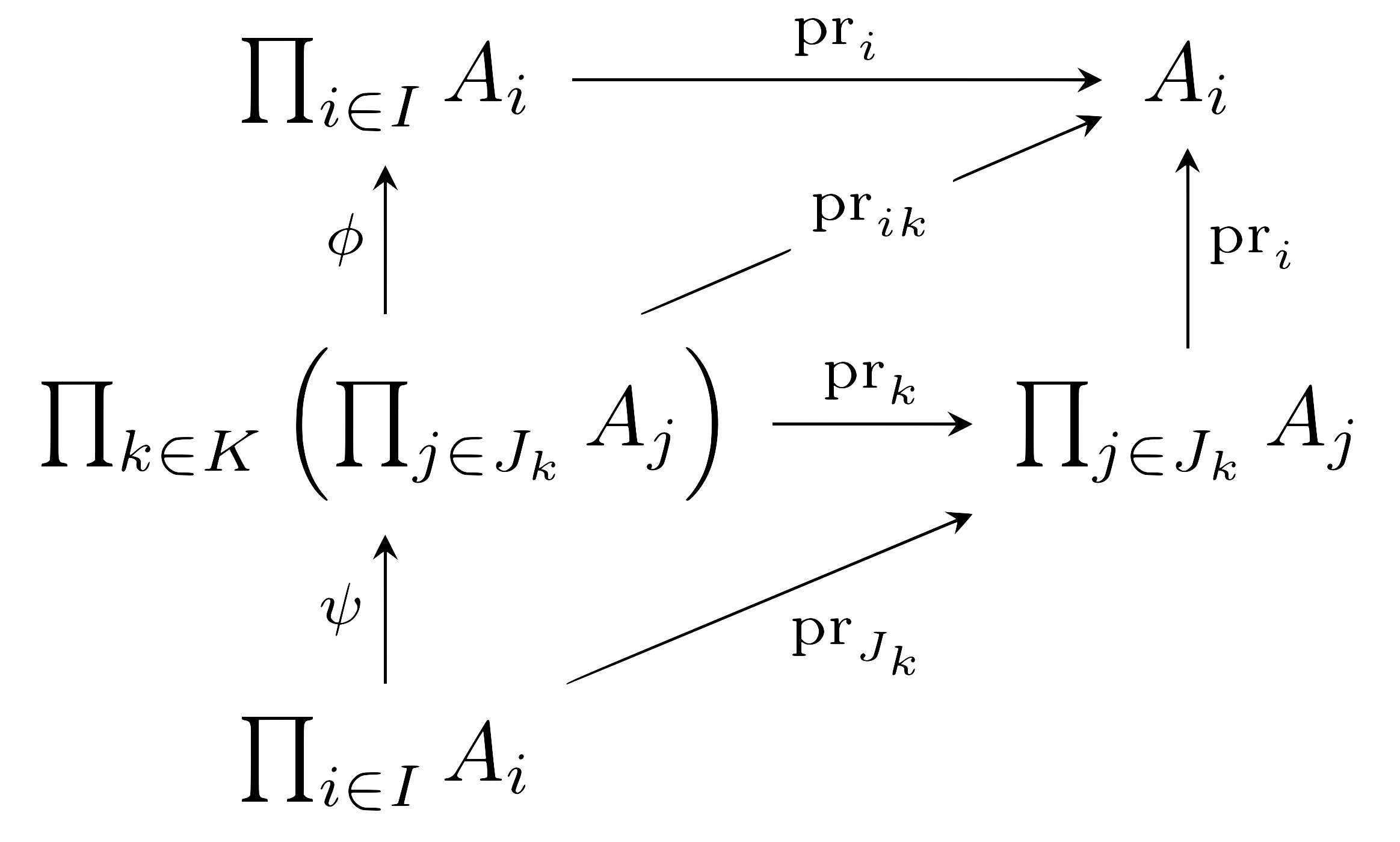
\((A_i)_{i\in I}\), \((B_i)_{i\in I}\)가 같은 index를 갖는 family이고, 함수들의 family \((g_i:A_i\rightarrow B_i)_{i\in I}\)가 주어졌다 하자. \(u_f:I\rightarrow\bigcup_{i\in I}B_i\)를 \(i\mapsto g_i(f(i))\)로 정의하면 \(u_f(i)\in B_i\)이고, 따라서 \(u_f\in\prod_{i\in I}B_i\)이다.
정의 4 위에서 정의한 함수 \(f\mapsto u_f\)를 \((g_i)\)들의 곱product이라 하고, \(\prod_{i\in I}g_i\)으로 적는다.
명제 5 \((A_i)_{i\in I}\), \((B_i)_{i\in I}\), \((C_i)_{i\in I}\)가 세 family라 하고, \((f_i)_{i\in I}\), \((g_i)_{i\in I}\)가 각각 \(A_i\)에서 \(B_i\), \(B_i\)에서 \(C_i\)로의 함수들의 family라 하자. 그럼
\[\prod_{i\in I} (g_i\circ f_i)=\left(\prod_{i\in I} g_i\right)\circ\left(\prod_{i\in I}f_i\right)\]이 성립한다.
증명
다음 두 개의 commutative diagram 이외에는 특별히 설명할 것이 없다.
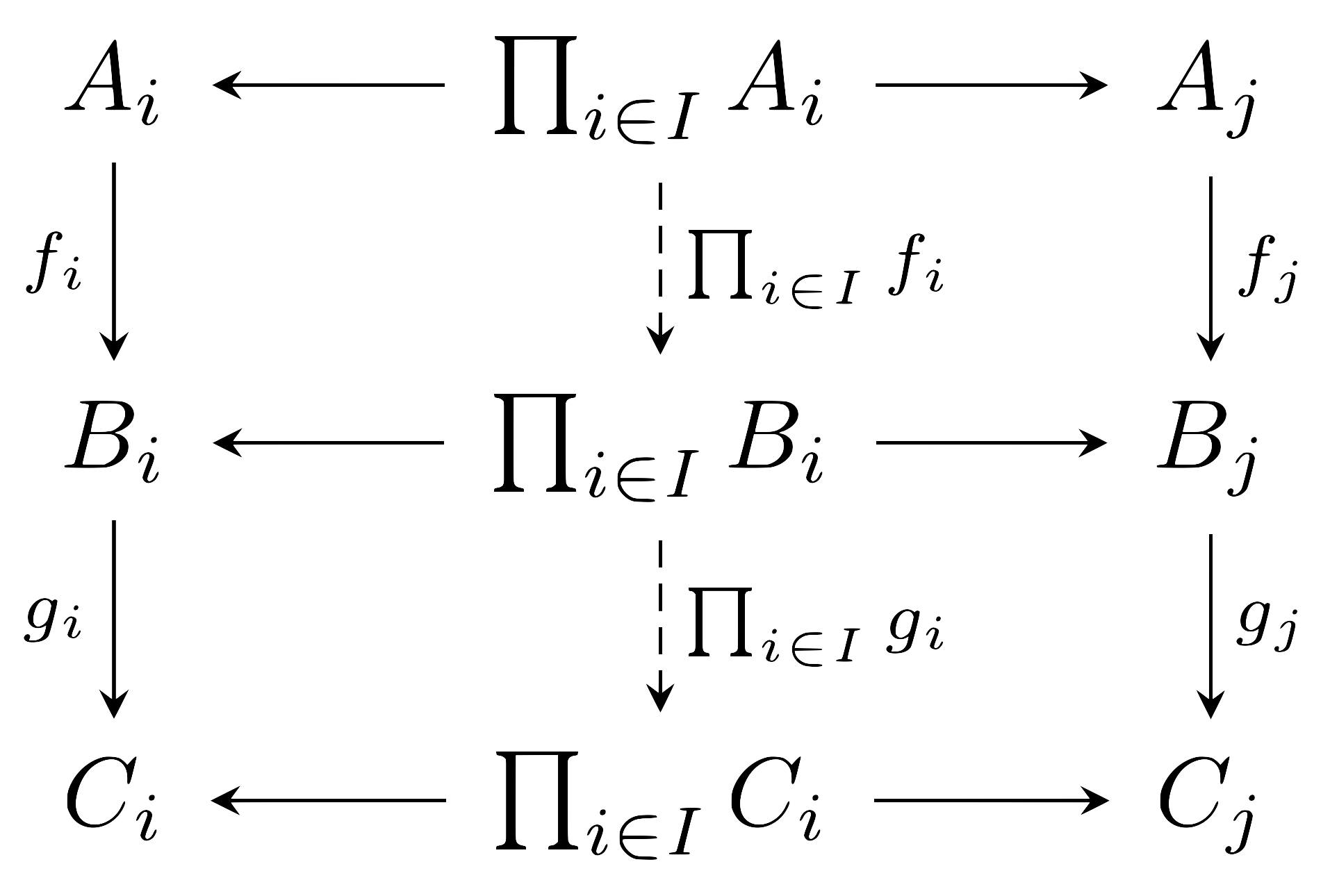
그리고
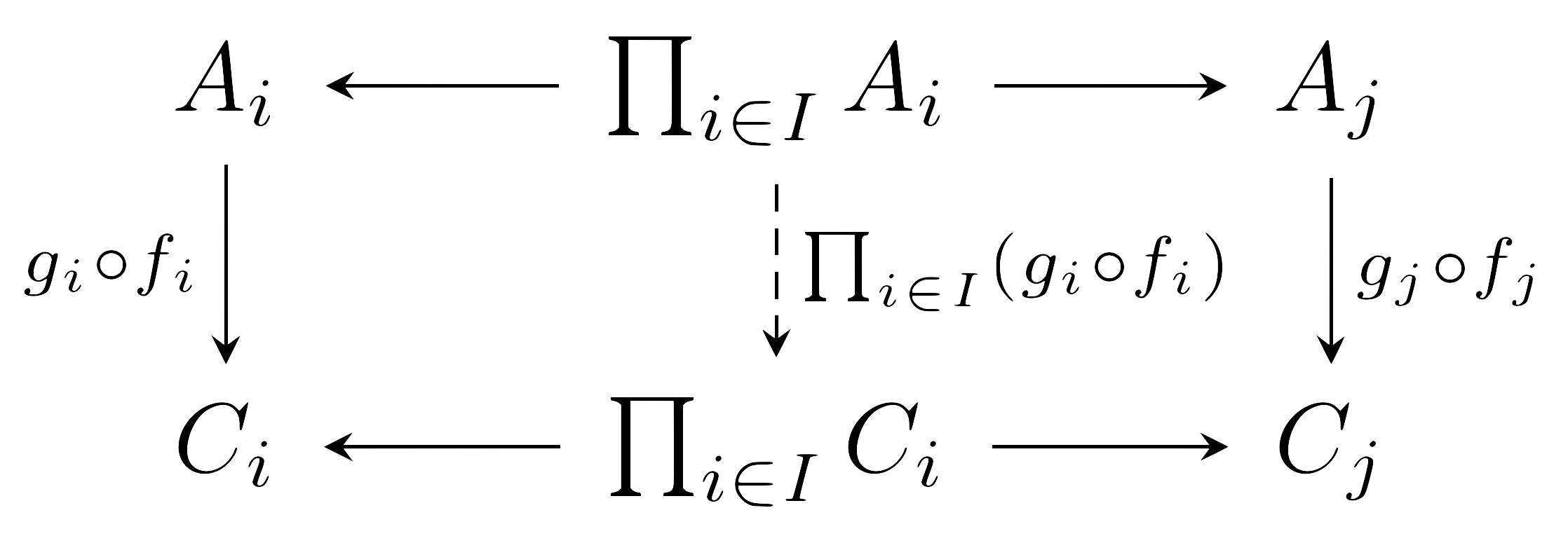
\(\id_{A_i}\)들의 곱이 \(\id_{\prod A_i}\)라는 것은 자명하므로, 위의 명제에 의해 단사함수들의 곱은 단사함수이고 전사함수들의 곱은 전사함수라는 것 또한 명확하다.
연산들 사이의 분배법칙
한편, 둘 이상의 연산이 정의되어 있다면 분배법칙이 성립하는지가 중요한 관심사다.
명제 6 \(((A_{k,i})_{i\in J_k})_{k\in K}\)가 집합들의 family들의 family라 하자. 추가로 \(K\neq\emptyset\)이고, \(J_k\neq\emptyset\)가 모든 \(k\in K\)에 대해 성립한다고 하자. 그럼 \(I=\prod_{k\in K} J_k\neq\emptyset\)에 대하여,
\[\bigcup_{k\in K}\left(\bigcap_{i\in J_k}A_{k,i}\right)=\bigcap_{f\in I}\left(\bigcup_{k\in K}A_{k,f(k)}\right),\quad\bigcap_{k\in K}\left(\bigcup_{i\in J}A_{k,i}\right)=\bigcup_{f\in I}\left(\bigcap_{k\in K}A_{k,f(k)}\right)\]이 성립한다.
증명
우선 \(x\in \bigcup_{k\in K}\left(\bigcap_{i\in J_k}A_{k,i}\right)\)라 하자. 우리는 \(x\in \bigcap_{f\in I}\left(\bigcup_{k\in K}A_{k,f(k)}\right)\), 즉 모든 \(f\in I\)에 대하여 \(x\in \bigcup_{k\in K}A_{k,f(k)}\)임을 보여야 한다. 어떤 \(k\in K\)에 대하여 \(x\in \bigcap_{i\in J_k}A_{k,i}\)이므로, \(x\in A_{k,f(k)}\)이다. 따라서 \(x\in \bigcup_{k\in K}A_{k,f(k)}\)가 모든 \(f\)에 대하여 성립하고, 따라서 포함관계가 성립한다.
반대쪽 포함관계를 보이기 위해 대우명제를 사용하자. 즉 \(x\not\in \bigcup_{k\in K}\left(\bigcap_{i\in J_k}A_{k,i}\right)\)라 하자. 그럼 모든 \(k\in K\)에 대하여, \(x\not\in \bigcap_{i\in J_k}A_{k,i}\)이다. 따라서 어떤 \(i\)가 존재하여, 모든 \(k\)에 대해 \(x\not\in A_{k,i}\)이다. 이제 \(f(k)\)가 그러한 \(i\)가 되도록 하는 \(f\in I\)를 잡으면, \(x\not\in\bigcup_{k\in K}A_{k,f(k)}\)이고 , 따라서 우변에 속하지 않는다. 두 번째 식도 이와 비슷하게 보이면 된다.
Product와 union, 그리고 product와 intersection 사이에도 다음과 같이 분배법칙이 성립하며, 이에 대한 증명은 위와 거의 같으므로 생략한다.
명제 7 \(((A_{k,i})_{i\in J_k})_{k\in K}\)가 집합들의 family들의 family이고, \(I\)를 위의 명제와 동일하게 정의하자. 그럼
\[\prod_{k\in K}\left(\bigcup_{i\in J_k}A_{k,i}\right)=\bigcup_{f\in I}\left(\prod_{k\in K}A_{k,f(k)}\right),\quad\prod_{k\in K}\left(\bigcap_{i\in J}A_{k,i}\right)=\bigcap_{f\in I}\left(\prod_{k\in K}A_{k,f(k)}\right)\]가 성립한다.
참고문헌
[Bou] N. Bourbaki, Theory of Sets. Elements of mathematics. Springer Berlin-Heidelberg, 2013.

댓글남기기