순서집합의 원소들

다음의 diagram

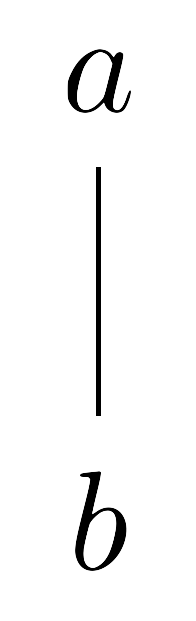
이 $b\leq a$를 뜻하는 것이라 하자. 예를 들어, 다음의 diagram

은 $b\leq a$이고 $c\leq a$이지만, $b$와 $c$ 사이에는 별 관계가 없는 상황을 나타낸다. 이러한 diagram을 Hasse diagram이라 부른다.

극대원소와 극소원소

정의 1 Ordered set $A$의 원소 $a$가 $A$의 minimal element_극소원소 (resp. maximal element_극대원소)라는 것은 모든 $x\in A$에 대하여 $a\leq x$ (resp. $a\geq x$)이면 $x=a$가 성립하는 것이다.

Minimal element가 유일할 필요는 없다. 예컨대

에서, $b$와 $c$는 모두 집합 $\{a,b,c\}$의 minimal element이다. 수학자들은 보통 이런 성질을 가지는 원소가 유일하기를 바라므로, 이 상황은 그렇게 달가운 상황이 아니다.

최대원소와 최소원소

정의 2 Ordered set $A$의 원소 $a$가 $A$의 least element_최소원소 (resp. greatest element_최대원소)라는 것은 모든 $x\in A$에 대해서 $a\leq x$ (resp. $x\leq a$)인 것이다.

앞선 예시에서, $b$와 $c$는 least element가 될 수 없다. $b\leq c$와 $c\leq b$가 성립하지 않기 때문이다. 정의에 의해 least element는 유일하다. 더욱이 다음이 성립한다.

명제 3 만일 $A$가 least element $a$를 갖는다면, $a$는 $A$의 유일한 minimal element이다.

증명

$A$의 임의의 원소 $x$에 대하여 $a\leq x$가 성립한다. 따라서 만일 $x\leq a$가 성립하는 $x\in A$가 존재한다면, $\leq$의 antisymmetry로부터 $x=a$여야 한다. 이로부터 $a$가 $A$의 minimal element가 된다는 것을 안다.

만일 $a’$가 $A$의 다른 minimal element이고, $a’\neq a$라면 정의 1의 대우명제로부터 $a’\not\leq a$여야 하는데, 이는 $a$가 least element라는 사실에 모순이므로 $a’=a$여야 한다.

때때로 ordered set의 모든 원소보다 큰 새로운 원소, 혹은 모든 원소보다 작은 새로운 원소를 생각해야 할 필요가 있다. 이러한 가상의 원소는 $\pm\infty$으로 쓰는 것이 보편적이다.

명제 4 $A$가 ordered set이고 $A’=A\sqcup\{+\infty\}$이라 하자. 그럼 $A$에서 정의된 order relation을 확장하며, $a$를 greatest element로 갖는 $A’$의 order relation이 존재한다.

증명

기존의 order relation에 $\bigcup_{x\in A}\left\{(x, +\infty)\right\}$의 원소들을 추가해주면 된다.

상한과 하한

정의 5 Preordered set $A$와 그 부분집합 $X$가 주어졌다 하자. $a\in A$가 모든 $x\in X$에 대해 $a\leq x$ (resp. $a\geq x$)를 만족한다면, 이를 $A$에서의 $X$의 lower bound_하계 (resp. upper bound_상계)라 부른다.

Lower bound (resp. upper bound)를 갖는 집합을 bounded below_{아래로 유계} (resp. bounded above_{위로 유계})라 하고, bounded below이면서 bounded above인 집합을 간단히 bounded_유계라 한다.

다음의 ordered set $A=\{a,b,c,d,e\}$를 생각하자.

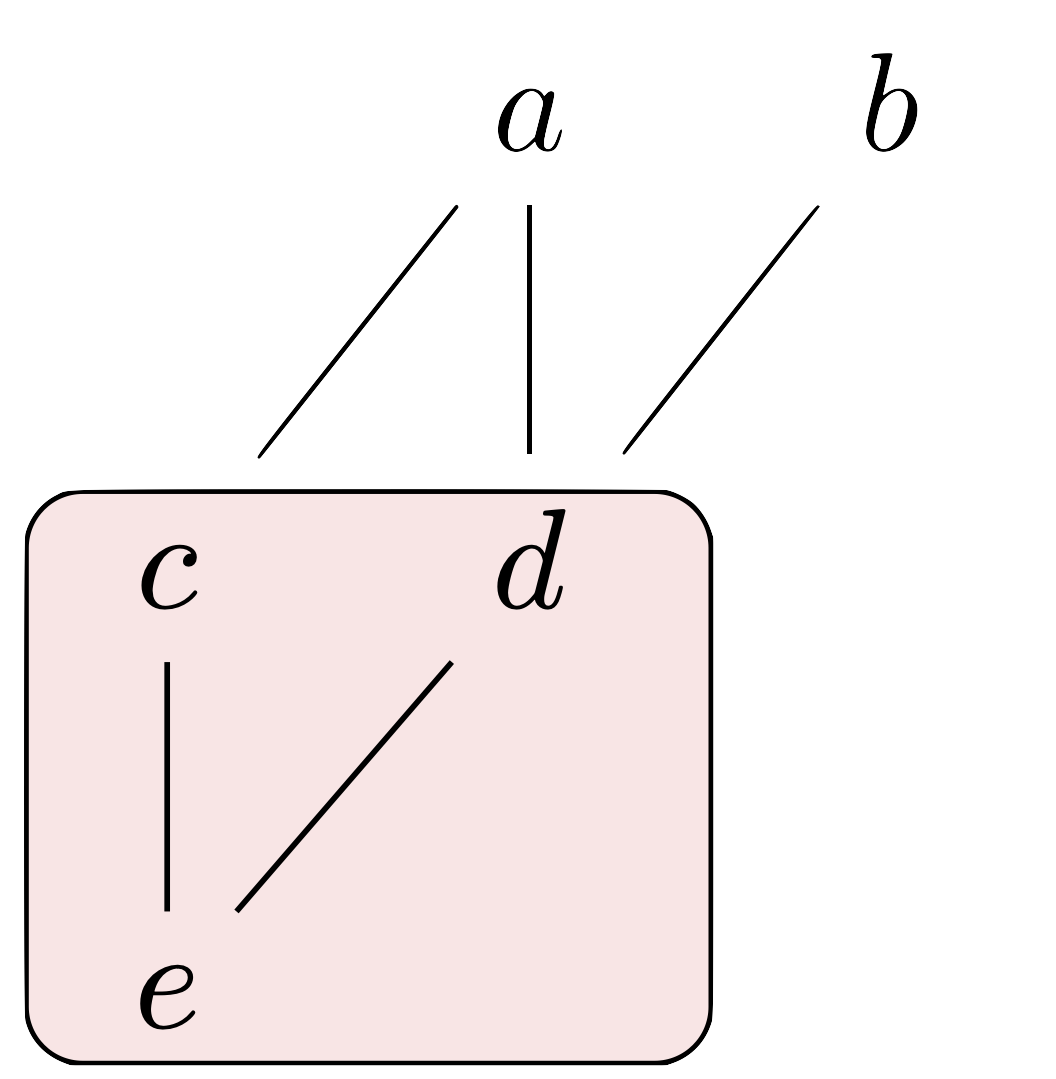
그럼 $a$는 집합 $X=\left\{c,d,e\right\}$의 upper bound지만 $b$는 그렇지 않다. 집합 $X’=\left\{d,e\right\}$를 생각한다면, $a$와 $b$ 모두가 이 집합의 upper bound이다. 위의 예시로부터 집합 $X$의 lower bound가 $X$에 포함될 필요는 없지만, 만일 이것이 성립한다면 그 원소는 $X$의 least element가 된다.

정의 6 $A$가 ordered set이고 $X\subseteq A$이라 하자. $A$의 어떤 원소 $a$가 $X$의 greatest lower bound_최대하계 (혹은 infimum_하한)라는 것은 이 원소가 $X$의 lower bound 중 greatest element라는 것이다. 이와 유사하게 least upper bound_최소상계 (혹은 supremum_상한)도 정의한다.

$X\subseteq A$의 supremum이 존재한다면, 이를 $\sup_AX$로 쓰고, infimum은 $\inf_AX$로 쓴다. 정의에 의하여, $X\subseteq A$가 greatest element $a$를 갖는다면 $a=\sup_AX$임을 쉽게 확인할 수 있다.

명제 7 $A$가 ordered set이고 $X\subset A$가 supremum과 infimum을 모두 갖는다 하자.

1. 만일 $X\neq\emptyset$일 경우 $\inf_A X\leq\sup_A X$이다.
2. 만일 $X=\emptyset$이라면, $\sup_AX$와 $\inf_AX$는 각각 $A$의 least, greatest element가 된다.

증명

1. 만일 $X\neq\emptyset$라면 적어도 하나의 원소가 존재한다. 이를 $a$라 하자. 그럼 정의에 의해 $\inf X\leq a$이고 $a\leq\sup X$이며 transitivity에 의해 $\inf_AX \leq\sup_AX$이다.
2. 만일 $X=\emptyset$라면, $A$의 임의의 원소 $a$는 모든 $x\in X$에 대하여 $a\leq x$ 그리고 $x\leq a$를 만족한다. 따라서 $A$의 임의의 원소는 $X$의 lower bound이자 upper bound가 되며, $\sup_AX$와 $\inf_AX$는 $A$의 least, greatest element가 된다.

상한, 하한과 집합간의 연산

이제 지금까지 살펴본 집합의 연산과 상한, 하한의 관계를 살펴본다.

명제 8 Ordered set $A$의 두 부분집합 $X,X’$에 대하여, $\sup_AX,\sup_AX’$가 각각 정의되고 $X’\subseteq X$라면 $\sup X’\leq\sup X$이다.

증명

$x\in X’$를 임의로 택하자. $X’\subseteq X$이므로, $x\in X$이다. 한편 임의의 $x\in X$에 대하여 $x\leq \sup X$가 성립하고 따라서 $\sup X$는 $X’$의 upper bound이다. 이제 정의에 의해 $\sup X’\leq \sup X$이다.

명제 9 Ordered set $A$에 대해, 모든 $i\in I$에 대해 $x_i\leq y_i$를 만족하는 family $(x_i)_{i\in I}$, $(y_i)_{i\in I}$를 생각하자. 이들이 모두 $A$에서 supremum을 갖는다면, $\sup_{i\in I} x_i\leq \sup_{i\in I} y_i$이다.

증명

임의의 $i\in I$에 대하여, $x_i\leq y_i$이고 $y_i\leq \sup y_i$이므로 모든 $i$에 대해 $x_i\leq \sup y_i$이고 따라서 $\sup x_i$의 minimality에 의해 $\sup x_i\leq\sup y_i$이다.

명제 10 Ordered set $A$와 index set $I$, 그리고 $I$의 covering $(J_k)_{i\in I}$에 대하여, $(x_i)_{i\in J_k}$가 $A$에서 supremum을 갖는다 하자. 그럼 $\sup_{i\in I} x_i$가 존재하는 것은 $\sup_{k\in K}(\sup_{j\in J_k}x_j)$가 존재하는 것과 동치이며 두 값은 같다.

증명

$b_k=\sup_{i\in J_k} x_i$라 적자. 우선 $(x_i)_{i\in I}$가 supremum을 갖는다고 하고, 이를 $a$라 하자. 그럼 $a\leq b_k$가 모든 $k$에 대해 성립한다. 또, 만약 $c\geq b_k$가 모든 $k$에 대해 성립한다면, 임의의 $x_i$에 대해서 $i\in J_{k’}$인 $k’$는 $b_{k’}\geq x_i$를 만족하고, 따라서 어떠한 $i$에 대해서도 $c\geq x_i$이다. 이제 $a$의 최소성에 의해 $c\geq a$이어야 하고, 따라서 $a$가 supremum이며 $\sup_{i\in I}x_i=\sup_{k\in K}(\sup_{i\in J_k} x_j)$이다.

반대로 $(b_k)_{k\in K}$가 supremum $a’$를 갖는다 해도 위와 같은 방법으로 증명을 완료할 수 있다.

명제 11 Ordered set $(A_i)_{i\in I}$들의 곱 $A=\prod A_i$와 그 부분집합 $X$에 대해 $X_i=\pr_i X$라 하자. 그럼 $\sup_AX$가 존재하는 것과 각각의 $\sup_{A_i}X_i$가 존재하는 것은 동치이며, $\sup_AX=(\sup_{A_i}X_i)$이다.

증명

우선 $\sup_{A_i} X_i$가 각각의 $i$에 대해 존재한다고 하자. 그럼 $(\sup_{A_i} X_i)_{i\in I}$가 $X$의 upper bound임은 자명하다. 만일 $(c_i)$가 $X$의 다른 upper bound였다면, 각각의 $c_i$는 $X_i$의 upper bound가 될 것이므로 $\sup_{A_i}X_i$의 최소성에 의해 $c_i\geq\sup X_i$이고, 따라서 $(c_i)\geq(\sup X_i)_{i\in I}$이다.

반대로 $\sup X=(a_i)$가 존재한다고 하자. 모든 $i$에 대해서, $a_i$는 $X_i$의 upper bound이다. 만일 $x_i\in X_i$라면, $i$번째 성분으로 $x_i$를 갖는 $x\in X$가 $x\leq (a_i)$이도록 하는 $x$가 존재하기 때문이다. 이제 임의의 다른 upper bound $a_i’$에 대해, 새로운 원소 $(c_i)$를 $(a_i)$의 $i$번째 성분을 $a_i’$로 바꾸어 정의하면 $c\geq a$이므로 $a_i’\geq a_i$가 된다.

참고 Ordered set $A$와 $X’\subseteq X\subseteq A$에 대해서, $\sup_AX’$와 $\sup_XX’$ 중 하나만 존재할 수도 있고, 둘 다 존재하지만 값이 다를 수도 있다. 예컨대 $X’=\{x\in\mathbb{Q}\mid x < \sqrt{2}\}$를 각각의 집합들에서 비교해보자.

1. $X_1=\mathbb{Q}$의 부분집합으로써, 이 집합의 supremum은 존재하지 않으나 $A=\mathbb{R}$에서는 존재한다. 즉 $\sup_AX’$가 존재하더라도 $\sup_{X_1}X’$는 존재하지 않을 수도 있다.
2. 한편 집합 $X_2=X’\cup \left\{2\right\}$를 생각하자. 그럼 $X’\subseteq X_2\subseteq X_1$이고 $\sup_{X_2}X’=2$이지만 $\sup_{X_1}A$는 존재하지 않는다.
3. 마지막으로 $X’\subseteq X_2\subseteq A$에서, $\sup_{X_2}X’$와 $\sup_AX’$는 각각 존재하지만 두 값은 다르다.

그러나 여전히 다음을 증명할 수 있다.

명제 12 $A$가 ordered set이고, $X’\subseteq X\subseteq A$이라 하자. 만일 $\sup_AX’$와 $\sup_XX’$이 모두 존재한다면 $\sup_AX’\leq\sup_XX’$이다. 만일 $\sup_AX’$이 존재하고 $X$에 속한다면 $\sup_XX’$도 존재하고 이 값은 $\sup_AX’$와 같다.

증명

$X’$의 $X$에서의 upper bound들의 집합은 $A$에서의 upper bound들의 집합에 포함되고, 따라서 supremum은 더 크다. 만일 $\sup_AX’$가 존재하고 $X$에 속한다면, 이는 자명하게 $X$에서의 $X’$의 supremum이 된다.

---

참고문헌

[Bou] N. Bourbaki, Theory of Sets. Elements of mathematics. Springer Berlin-Heidelberg, 2013.

---