지난 글에서 각각 \(n\)차원, \(m\)차원인 두 \(\mathbb{K}\)-벡터공간 \(V,W\)에 대하여 \(\Hom(V,W)\)는 \(mn\)차원 \(\mathbb{K}\)-벡터공간이 된다는 것을 살펴보았다. 또 \(m\times n\) 행렬들의 공간 \(\Mat_{m\times n}(\mathbb{K})\) 또한 \(mn\)차원의 \(\mathbb{K}\)-벡터공간이다. 그럼 §동형사상, ⁋따름정리 4로부터 이 두 벡터공간이 isomorphic하다는 것을 안다.
이번 글에서 증명할 선형대수학의 기본정리1는 이들이 단순히 같은 차원을 갖는 벡터공간이기 때문에 isomorphic할 뿐만 아니라, 이들 사이의
기본정리: 유클리드 공간
§선형사상들의 공간에서 우리는 다음의 식
\[\begin{aligned}L(x_1)&=\alpha_{11}y_1+\alpha_{21}y_2+\cdots+\alpha_{m1}y_m\\L(x_2)&=\alpha_{12}y_1+\alpha_{22}y_2+\cdots+\alpha_{m2}y_m\\&\phantom{a}\vdots\\L(x_n)&=\alpha_{1n}y_1+\alpha_{2n}y_2+\cdots+\alpha_{mn}y_m\end{aligned}\]을 만족하는 linear map \(L\)을 다음의 대응
\[v=\sum_{i=1}^n v_ix_i\quad\mapsto\quad \sum_{j=1}^m\left(\sum_{i=1}^n\alpha_{ji}v_i\right)y_j=L(v)\tag{1}\]으로 이해하기로 하였다. 특히 만일 \(V=\mathbb{K}^n\), \(W=\mathbb{K}^m\)이고, 이들 각각에 standard basis \(\mathcal{E}_n=\{e_1,\ldots, e_n\},\mathcal{E}_m=\{e_1,\ldots,e_m\}\)가 주어졌다 하면 위의 대응은
\[\begin{pmatrix}v_1\\v_2\\\vdots\\v_n\end{pmatrix}\quad\mapsto\quad\begin{pmatrix}\sum_{i=1}^n\alpha_{1i}v_i\\\sum_{i=1}^n\alpha_{2i}v_i\\\vdots\\\sum_{i=1}^n\alpha_{mi}v_i\end{pmatrix}\]으로 쓸 수 있다. 그런데 우변은 정확히 행렬과 벡터의 곱
\[\begin{pmatrix}\alpha_{11}&\alpha_{12}&\cdots&\alpha_{1n}\\\alpha_{21}&\alpha_{22}&\cdots&\alpha_{2n}\\\vdots&\vdots&\ddots&\vdots\\\alpha_{m1}&\alpha_{m2}&\cdots&\alpha_{mn}\end{pmatrix}\begin{pmatrix}v_1\\v_2\\\vdots\\v_n\end{pmatrix}\tag{2}\]과 동일한 모양이다. 위의 식에서의 \(m\times n\) 행렬을 \(\mathcal{E}_n,\mathcal{E}_m\)에 대한 \(L\)의 행렬표현이라 부르고, 이를 \([L]^{\mathcal{E}_n}_{\mathcal{E}_m}\)로 적는다.
반대로 \(m\times n\) 행렬은 똑같은 방식으로 linear map을 지정해준다는 것을 확인할 수 있다.
예시 1 유클리드 \(n\)-공간 \(\mathbb{K}^n\)과, 행렬 \(A\in\Mat_{m\times n}(\mathbb{K})\)를 생각하자. 임의의 \(x\in\mathbb{K}^n\)에 대하여, \(L_A(x)\)를 다음의 식
\[L_A(x)=Ax\]으로 정의하면, \(L_A\)는 \(\mathbb{K}^n\)에서 \(\mathbb{K}^m\)으로의 linear map이 된다.
\(\mathbb{K}^n\)에서 \(\mathbb{K}^m\)으로의 임의의 linear map \(L\)이 주어졌다 하자. 어렵지 않게 \(L=L_{[L]^{\mathcal{E}_n}_{\mathcal{E}_m}}\)임을 확인할 수 있다. 따라서 다음의 대응이 존재한다.
\[\{\text{linear maps from $\mathbb{K}^n$ to $\mathbb{K}^m$}\}\longleftrightarrow\Mat_{m\times n}(\mathbb{K})\]더 정확하게 말하자면 \(L\mapsto [L]^{\mathcal{E}_n}_{\mathcal{E}_m}\), 그리고 \(A\mapsto L_A\) (예시 1의 정의)이 서로의 역함수가 되는 전단사함수가 된다.
그런데 왼쪽의 집합은 \(\Hom(\mathbb{K}^n, \mathbb{K}^m)\)와 같으므로, 이 대응이 전단사인 linear map, 곧 isomorphism이 되는지를 확인해볼 수 있다. 이에 대한 답은 그렇다는 것이며, 이 다음의 정리 3과 함께 이 결과를 선형대수학의 기본정리라 부른다.
정리 2 \(\Hom(\mathbb{K}^n,\mathbb{K}^m)\cong\Mat_{m\times n}(\mathbb{K})\)
증명
주어진 함수 \(L\mapsto[L]^{\mathcal{E}_n}_{\mathcal{E}_m}\)가 linear임을 보여야 한다.
\(L_1,L_2\)가 모두 \(\Hom(\mathbb{K}^n,\mathbb{K}^m)\)의 원소라 하자. 그럼 각각의 \(e_i\in\mathcal{E}_n\)에 대하여,
\[\begin{aligned}L_1(e_1)&=\alpha_{1,1}e_1+\alpha_{2,1}e_2+\cdots+\alpha_{m,1}e_m\\L_1(e_2)&=\alpha_{1,2}e_1+\alpha_{2,2}e_2+\cdots+\alpha_{m,2}e_m\\&\vdots\\L_1(e_n)&=\alpha_{1,n}e_1+\alpha_{2,n}e_2+\cdots+\alpha_{m,n}e_m\end{aligned}\]그리고
\[\begin{aligned}L_2(e_1)&=\beta_{1,1}e_1+\beta_{2,1}e_2+\cdots+\beta_{m,1}e_m\\L_2(e_2)&=\beta_{1,2}e_1+\beta_{2,2}e_2+\cdots+\beta_{m,2}e_m\\&\vdots\\L_2(e_n)&=\beta_{1,n}e_1+\beta_{2,n}e_2+\cdots+\beta_{m,n}e_m\end{aligned}\]이도록 하는 스칼라들의 family \((\alpha_{i,j})\), \((\beta_{i,j})\)들이 존재한다. 이제,
\[\begin{aligned}(L_1+L_2)(e_1)&=(\alpha_{1,1}+\beta_{1,1})e_1+(\alpha_{2,1}+\beta_{2,1})e_2+\cdots+(\alpha_{m,1}+\beta_{m,1})e_m\\(L_1+L_2)(e_2)&=(\alpha_{1,2}+\beta_{1,2})e_1+(\alpha_{2,2}+\beta_{2,2})e_2+\cdots+(\alpha_{m,2}+\beta_{m,2})e_m\\&\vdots\\(L_1+L_2)(e_n)&=(\alpha_{1,n}+\beta_{1,n})e_1+(\alpha_{2,n}+\beta_{2,n})e_2+\cdots+(\alpha_{m,n}+\beta_{m,n})e_m\end{aligned}\]이고, 따라서 \(L_1+L_2\)의 행렬표현 \([L_1+L_2]^{\mathcal{E}_n}_{\mathcal{E}_m}\)은 정확히 \([L_1]^{\mathcal{E}_n}_{\mathcal{E}_m}+[L_2]^{\mathcal{E}_n}_{\mathcal{E}_m}\)이 된다. 이와 유사하게 스칼라곱에 대한 것도 성립한다.
뿐만 아니라 행렬들의 곱 또한 \(\Hom(\mathbb{K}^n,\mathbb{K}^m)\)에서 특별한 의미를 갖는다.
정리 3 세 유클리드 공간들 \(\mathbb{K}^n,\mathbb{K}^m,\mathbb{K}^k\)가 주어졌다 하자. 그럼 임의의 \(L_1:\mathbb{K}^n\rightarrow \mathbb{K}^m\), \(L_2:\mathbb{K}^m\rightarrow \mathbb{K}^k\)에 대하여 항상
\[[L_2\circ L_1]^{\mathcal{E}_n}_{\mathcal{E}_k}=[L_2]^{\mathcal{E}_m}_{\mathcal{E}_k}[L_1]^{\mathcal{E}_n}_{\mathcal{E}_m}\]이 성립한다. 즉, linear map의 합성은 행렬의 곱과 같다.
증명
좌변의 \([L_2\circ L_1]^{\mathcal{E}_n}_{\mathcal{E}_k}\)을 결정하기 위해서는 \(L_2\circ L_1\)에 의해 \(\mathcal{E}_n\)의 원소 \(e_i\)들이 어디로 옮겨지는지만 확인하면 된다. \(L_1\), \(L_2\)가 다음의 식
\[[L_1]^{\mathcal{E}_n}_{\mathcal{E}_m}=\begin{pmatrix}\alpha_{1,1}&\alpha_{1,2}&\cdots&\alpha_{1,n}\\\alpha_{2,1}&\alpha_{2,2}&\cdots&\alpha_{2,n}\\\vdots&\vdots&\ddots&\vdots\\\alpha_{m,1}&\alpha_{m,2}&\cdots&\alpha_{m,n}\end{pmatrix},\quad[L_2]^{\mathcal{E}_m}_{\mathcal{E}_k}=\begin{pmatrix}\beta_{1,1}&\beta_{1,2}&\cdots&\beta_{1,m}\\\beta_{2,1}&\beta_{2,2}&\cdots&\beta_{2,m}\\\vdots&\vdots&\ddots&\vdots\\\beta_{k,1}&\beta_{k,2}&\cdots&\beta_{k,m}\end{pmatrix}\]으로 주어졌다 하자. 약간의 계산을 하면,
\[\begin{aligned}(L_2\circ L_1)(e_i)&=L_2(\alpha_{1,i}e_1+\cdots+\alpha_{m,i}e_m)\\&=\alpha_{1,i}L_2(e_1)+\alpha_{2,i}L_2(e_2)+\cdots+\alpha_{m,i}L(e_m)\\&=\alpha_{1,i}(\beta_{1,1}e_1+\beta_{2,1}e_2+\cdots+\beta_{k,1}e_k)\\&\phantom{==}+\alpha_{2,i}(\beta_{1,2}e_1+\beta_{2,2}e_2+\cdots+\beta_{k,2}e_k)\\&\phantom{===}+\cdots\\&\phantom{====}+\alpha_{m,i}(\beta_{1,m}e_1+\beta_{2,m}e_2+\cdots+\beta_{k,m}e_k)\end{aligned}\]이제 위 식을 \(\mathbb{K}^k\)의 basis \(e_1,\ldots, e_k\)들끼리 묶으면,
\[(L_2\circ L_1)(e_i)=\left(\sum_{l=1}^m\alpha_{l,i}\beta_{1,l}\right)e_1+\cdots+\left(\sum_{l=1}^m\alpha_{l,i}\beta_{k,l}\right)e_k.\]\([L_2\circ L_1]^{\mathcal{E}_n}_{\mathcal{E}_k}\)의 \(i\)번째 열은 \(e_i\)가 \(L_2\circ L_1\)에 의해 옮겨지는 벡터이므로, 행렬 \([L_2\circ L_1]^{\mathcal{E}_n}_{\mathcal{E}_k}\)의 \(i\)열, \(j\)행은 이 벡터의 \(j\)번째 성분 \(\sum_{l=1}^m\alpha_{l,i}\beta_{j,l}\)이 된다. 이제 §행렬, ⁋정의 3 직후의 계산으로부터 이것이 두 행렬 \([L_2]_{\mathcal{E}_k}^{\mathcal{E}_m}\), \([L_1]_{\mathcal{E}_m}^{\mathcal{E}_n}\)의 곱의 \((i,j)\) 성분이라는 것을 안다.
기본정리: 일반적인 경우
앞서 우리가 증명한 기본정리는 유클리드 공간에 대해서만 적용되지만, 아주 작은 수정만 있으면 일반적인 유한차원 \(\mathbb{K}\)-벡터공간에 대해서도 성립한다. 이 과정은 다음의 diagram으로 간단하게 요약할 수 있다.
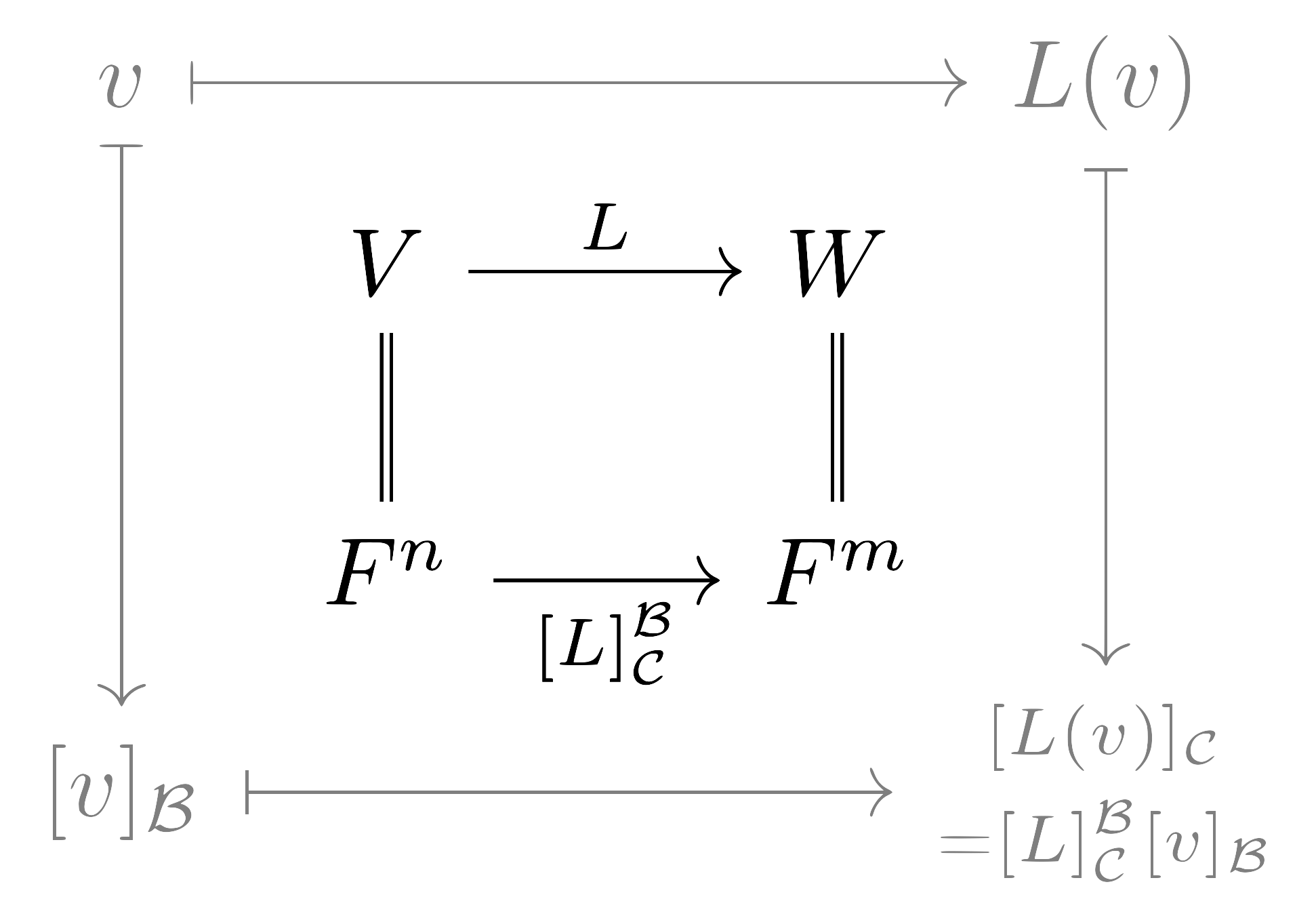
임의의 유한차원 \(\mathbb{K}\)-벡터공간 \(V\)와 그 basis \(\mathcal{B}=\{x_1,\ldots, x_n\}\)에 대해 정의된 좌표표현은 다음의 isomorphism
\[v=\sum_{i=1}^n v_ix_i\mapsto [v]_\mathcal{B}=\begin{pmatrix}v_1\\v_2\\\vdots\\v_n\end{pmatrix}\in\mathbb{K}^n\]이다. 비슷하게 또 다른 유한차원 \(\mathbb{K}\)-벡터공간 \(W\)과 그 basis \(\mathcal{C}=\{y_1,\ldots, y_m\}\)가 주어졌다 하고, linear map \(L:V\rightarrow W\)가 다음의 식
\[\begin{aligned}L(x_1)&=\alpha_{1,1}y_1+\alpha_{2,1}y_2+\cdots+\alpha_{m,1}y_m\\L(x_2)&=\alpha_{1,2}y_1+\alpha_{2,2}y_2+\cdots+\alpha_{m,2}y_m\\&\vdots\\L(x_n)&=\alpha_{1,n}y_1+\alpha_{2,n}y_2+\cdots+\alpha_{m,n}y_m\end{aligned}\]에 의해 결정된다 하자. 그럼 \(\mathcal{B},\mathcal{C}\)에 대한 \(L\)의 행렬표현 \([L]^\mathcal{B}_\mathcal{C}\)을 이번에는 다음의 식
\[[L]^\mathcal{B}_\mathcal{C}=\begin{pmatrix}\alpha_{1,1}&\alpha_{1,2}&\cdots&\alpha_{1,n}\\\alpha_{2,1}&\alpha_{2,2}&\cdots&\alpha_{2,n}\\\vdots&\vdots&\ddots&\vdots\\\alpha_{m,1}&\alpha_{m,2}&\cdots&\alpha_{m,n}\end{pmatrix}\]으로 정의한다. 이제 식 (2)와 식 (1)을 비교해보면 임의의 \(v\in V\)에 대해, \(L(v)\)의 \(\mathcal{C}\)에 대한 좌표표현은 다음의 식
\[[L(v)]_\mathcal{C}=[L]^\mathcal{B}_\mathcal{C}[v]_\mathcal{B}\tag{3}\]으로 주어진다는 것을 확인할 수 있다.
그럼 정리 2에 대한 일반적인 버전은 다음의 정리로 주어진다.
정리 4 \(\Hom(V,W)\cong \Mat_{m\times n}(\mathbb{K})\).
증명
\(V\), \(W\)의 기저 \(\mathcal{B}\), \(\mathcal{C}\)를 각각 고정하자. 함수 \(L\mapsto[L]^\mathcal{B}_\mathcal{C}\)가 linear임을 보여야 한다.
\(L_1,L_2\)가 모두 \(\Hom(V,W)\)의 원소라 하자. 그럼 각각의 \(x_i\in\mathcal{B}\)에 대하여,
\[\begin{aligned}L_1(x_1)&=\alpha_{1,1}y_1+\alpha_{2,1}y_2+\cdots+\alpha_{m,1}y_m\\L_1(x_2)&=\alpha_{1,2}y_1+\alpha_{2,2}y_2+\cdots+\alpha_{m,2}y_m\\&\vdots\\L_1(x_n)&=\alpha_{1,n}y_1+\alpha_{2,n}y_2+\cdots+\alpha_{m,n}y_m\end{aligned}\]그리고
\[\begin{aligned}L_2(x_1)&=\beta_{1,1}y_1+\beta_{2,1}y_2+\cdots+\beta_{m,1}y_m\\L_2(x_2)&=\beta_{1,2}y_1+\beta_{2,2}y_2+\cdots+\beta_{m,2}y_m\\&\vdots\\L_2(x_n)&=\beta_{1,n}y_1+\beta_{2,n}y_2+\cdots+\beta_{m,n}y_m\end{aligned}\]이도록 하는 스칼라들의 family \((\alpha_{i,j})\), \((\beta_{i,j})\)들이 존재한다. 이제,
\[\begin{aligned}(L_1+L_2)(x_1)&=(\alpha_{1,1}+\beta_{1,1})y_1+(\alpha_{2,1}+\beta_{2,1})y_2+\cdots+(\alpha_{m,1}+\beta_{m,1})y_m\\(L_1+L_2)(x_2)&=(\alpha_{1,2}+\beta_{1,2})y_1+(\alpha_{2,2}+\beta_{2,2})y_2+\cdots+(\alpha_{m,2}+\beta_{m,2})y_m\\&\vdots\\(L_1+L_2)(x_n)&=(\alpha_{1,n}+\beta_{1,n})y_1+(\alpha_{2,n}+\beta_{2,n})y_2+\cdots+(\alpha_{m,n}+\beta_{m,n})y_m\end{aligned}\]일 것이고, 따라서 \(L_1+L_2\)의 행렬표현 \([L_1+L_2]^\mathcal{B}_\mathcal{C}\)은 정확히 \([L_1]^\mathcal{B}_\mathcal{C}+[L_2]^\mathcal{B}_\mathcal{C}\)이 된다. 이와 유사하게 스칼라곱에 대한 것도 성립한다.
정리 3 또한 비슷한 일반화를 갖는다.
정리 5 세 개의 \(\mathbb{K}\)-벡터공간 \(V_1,V_2,V_3\)와 이들 각각의 basis \(\mathcal{B}_1=\{x_1,\ldots,x_n\}\), \(\mathcal{B}_2=\{y_1,\ldots, y_m\}\), \(\mathcal{B}_3=\{z_1,\ldots, z_k\}\)가 주어졌다 하자. 그럼 임의의 \(L_1:V_1\rightarrow V_2\), \(L_2:V_2\rightarrow V_3\)에 대하여 항상
\[[L_2\circ L_1]^{\mathcal{B}_1}_{\mathcal{B}_3}=[L_2]^{\mathcal{B}_2}_{\mathcal{B}_3}[L_1]^{\mathcal{B}_1}_{\mathcal{B}_2}\]이 성립한다. 즉, linear map의 합성은 행렬의 곱과 같다.
증명
좌변의 \([L_2\circ L_1]^{\mathcal{B}_1}_{\mathcal{B}_3}\)을 결정하기 위해서는 \(L_2\circ L_1\)에 의해 \(\mathcal{B}_1\)의 원소들이 어디로 옮겨지는지만 확인하면 된다. \(L_1\), \(L_2\)가 다음의 식
\[[L_1]^{\mathcal{B}_1}_{\mathcal{B}_2}=\begin{pmatrix}\alpha_{1,1}&\alpha_{1,2}&\cdots&\alpha_{1,n}\\\alpha_{2,1}&\alpha_{2,2}&\cdots&\alpha_{2,n}\\\vdots&\vdots&\ddots&\vdots\\\alpha_{m,1}&\alpha_{m,2}&\cdots&\alpha_{m,n}\end{pmatrix},\quad[L_2]^{\mathcal{B}_2}_{\mathcal{B}_3}=\begin{pmatrix}\beta_{1,1}&\beta_{1,2}&\cdots&\beta_{1,m}\\\beta_{2,1}&\beta_{2,2}&\cdots&\beta_{2,m}\\\vdots&\vdots&\ddots&\vdots\\\beta_{k,1}&\beta_{k,2}&\cdots&\beta_{k,m}\end{pmatrix}\]으로 주어졌다 하자. 약간의 계산을 하면,
\[\begin{aligned}(L_2\circ L_1)(x_i)&=L_2(\alpha_{1,i}y_1+\cdots+\alpha_{m,i}y_m)\\&=\alpha_{1,i}L_2(y_1)+\alpha_{2,i}L_2(y_2)+\cdots+\alpha_{m,i}L(y_m)\\&=\alpha_{1,i}(\beta_{1,1}z_1+\beta_{2,1}z_2+\cdots+\beta_{k,1}z_k)\\&\phantom{==}+\alpha_{2,i}(\beta_{1,2}z_1+\beta_{2,2}z_2+\cdots+\beta_{k,2}z_k)\\&\phantom{===}+\cdots\\&\phantom{====}+\alpha_{m,i}(\beta_{1,m}z_1+\beta_{2,m}z_2+\cdots+\beta_{k,m}z_k)\end{aligned}\]이제, 위 식을 \(z\)들끼리 묶으면,
\[(L_2\circ L_1)(x_i)=\left(\sum_{l=1}^m\alpha_{l,i}\beta_{1,l}\right)z_1+\cdots+\left(\sum_{l=1}^m\alpha_{l,i}\beta_{k,l}\right)z_k\]앞서 우리는 \([L_2\circ L_1]^{\mathcal{B}_1}_{\mathcal{B}_3}\)의 \(i\)번째 열은 정확히 \(x_i\)가 \(L_2\circ L_1\)이 옮겨지는 벡터의 \(\mathcal{B}_3\)에서의 좌표표현이라는 것을 확인했으므로, 행렬 \([L_2\circ L_1]^{\mathcal{B}_1}_{\mathcal{B}_3}\)의 \(i\)열, \(j\)행은 이 벡터의 \(j\)번째 성분 \(\sum_{l=1}^m\alpha_{l,i}\beta_{j,l}\)이 된다. 앞서 정리 3에서와 마찬가지로 이 성분은 행렬곱 \([L_2]^{\mathcal{B}_2}_{\mathcal{B}_3}[L_1]^{\mathcal{B}_1}_{\mathcal{B}_2}\)의 \((i,j)\)번째 성분이므로 증명이 완료된다.
위의 정리 4는 \(V,W\)에 대한 basis를 선택하기만 하면 \(\Hom(V,W)\)와 \(\Mat_{m\times n}(\mathbb{K})\)를 같은 것으로 취급할 수 있다는 것을 보여준다. 예컨대 \(\Mat_{m\times n}(\mathbb{K})\)의 \(mn\)개의 basis는 §선형사상들의 공간, ⁋명제 5에서 살펴본 \(mn\)개의 basis에 대응된다. 다음 따름정리 또한 기본정리의 결과이다.
따름정리 6 두 \(n\)차원 \(\mathbb{K}\)-벡터공간 \(V,W\)가 주어졌다 하고, 이들의 기저 \(\mathcal{B},\mathcal{C}\)를 고정하자. 그럼 임의의 \(L\in\Hom(V,W)\)에 대하여, \(L^{-1}\in\Hom(W,V)\)의 기저 \(\mathcal{C},\mathcal{B}\)에 대한 행렬표현 \([L^{-1}]^{\mathcal{C}}_{\mathcal{B}}\)은 행렬 \([L]^{\mathcal{B}}_\mathcal{C}\)의 역행렬과 같다.
증명
역행렬과 역함수의 유일성에 의하여 자명.
이와 같이 §행렬에서 정의한 대부분의 개념들을 \(\Hom(V,W)\)로 옮겨올 수 있다. 곧바로 옮겨올 수 없는 개념 중 하나는 전치행렬 \(A^t\)인데, 이는 나중에 쌍대공간을 살펴보면 그 의미를 알 수 있다.
기저변환 행렬
정리 4를 한 마디로 요약하자면, \(n\)차원 벡터공간 \(V\)에서 \(m\)차원 벡터공간 \(W\)로의 linear map은, 이들 각각의 basis \(\mathcal{B}, \mathcal{C}\)를 고정하면, 이를 \(m\times n\)로 나타낼 수 있고 거꾸로 임의의 \(m\times n\) 행렬 또한 linear map으로 이해할 수 있다는 것이다. 그렇다면 자연스러운 질문 중 하나는 우리가 basis를 바꾸었을 때 어떠한 일이 생기는지이며, 이는 사실 정리 5에 이미 그 답이 나와있다.
정의 7 임의의 유한차원 \(\mathbb{K}\)-벡터공간 \(V\)와, \(V\)의 두 basis \(\mathcal{B},\mathcal{B}'\)에 대하여, \(\mathcal{B}\)에서 \(\mathcal{B}'\)로의 기저변환행렬change-of-basis matrix은
\[[\id_V]_{\mathcal{B}'}^\mathcal{B}\]를 의미한다.
벡터공간의 차원이 잘 정의된다는 것으로부터 이러한 행렬은 반드시 정사각행렬이 되어야 한다는 것이 자명하다. 또, 다음의 식
\[I=[\id_V]^{\mathcal{B}}_{\mathcal{B}}=[\id_V]_{\mathcal{B}}^{\mathcal{B}'}[\id_V]^\mathcal{B}_{\mathcal{B}'}\]으로부터 이러한 행렬은 항상 가역이라는 것을 알 수 있다.
기저변환행렬이 어떤 방식으로 작동하는지를 살펴보기 위해 유한차원 \(\mathbb{K}\)-벡터공간 \(V\)를 고정하고, \(V\) 위에 정의된 두 basis \(\mathcal{B},\mathcal{B}'\)가 주어졌다 하자. 선형대수학의 기본정리는 다음의 diagram이 commute한다는 것을 의미한다.
이 때 두 개의 수직방향 함수는 각각 \(v\mapsto [v]_\mathcal{B}\)와 \(v\mapsto[v]_{\mathcal{B}'}\)를 의미한다. 따라서 기저변환행렬은 \(v\in V\)의 \(\mathcal{B}\)에 대한 좌표표현을 받아, \(\mathcal{B}'\)에 대한 좌표표현으로 바꾸어주는 행렬이라 생각할 수 있다. 더 일반적으로 임의의 linear map \(L:V\rightarrow W\)가 주어졌다 하고, \(V,W\)의 basis \(\mathcal{B},\mathcal{C}\), 그리고 또 다른 basis \(\mathcal{B}',\mathcal{C}'\)가 주어졌다 하면, 선형대수학의 기본정리로부터 다음의 식
\[[L]_{\mathcal{C}'}^{\mathcal{B}'}=[\id_W]_{\mathcal{C}'}^\mathcal{C}[L]_{\mathcal{C}}^\mathcal{B}[\id_V]^{\mathcal{B}'}_{\mathcal{B}}\]를 얻는다.
두 \(m\times n\) 행렬 \(A,B\)가 주어졌다 하자. 그럼 위의 식에서부터, 만일 적당한 두 가역행렬 \(P,Q\)가 존재하여 다음의 식
\[B=PAQ\]를 만족한다면 \(A\)와 \(B\)를 같은 것으로 취급하고 싶은 유혹이 있다. 이는 고정된 linear map \(L\)이 주어졌을 때, \(L\)의 정의역과 공역의 basis를 잘 택하여 얻어지는 행렬표현들을 모두 같은 것으로 생각한다는 것이다.
그러나 이렇게 그럴듯한 동기에 비해 그 결과는 별로 좋지 않다. \(L\)의 정의역과 공역의 basis를 모두 변화시킬 수 있다면, 정의역의 임의의 basis \(\{x_1,\ldots, x_n\}\)을 택하고, 이후 공역에서는 \(L(x_1),\ldots, L(x_n)\)들 중 일차독립인 \(L(x_1),\ldots, L(x_k)\)를 택한 후 §벡터공간의 차원, ⁋명제 6을 이용하여 공역의 basis를 만들면 이 linear map은 항상 블록행렬
\[\begin{pmatrix}I&O\\O&O\end{pmatrix}\]꼴로 나타낼 수 있기 때문이다. 즉, 이런 식으로 \(L\)의 행렬표현을 분류한다면 여기에 영향을 미치는 것은 오직 \(L\)의 rank 뿐이다.
따라서 우리는 이 동치관계보다 세밀한 관계를 정의해야 한다.
정의 8 임의의 \(n\times n\) 행렬 \(A,B\)가 주어졌다 하자. 그럼 \(A\)와 \(B\)가 닮은 행렬similar matrix이라는 것은 적당한 가역행렬 \(P\)가 존재하여 \(A=PBP^{-1}\)이 성립하는 것이다.
즉 행렬 \(A,B\)가 닮은 행렬이라는 것은, 고정된 벡터공간 \(V\)에 대해 \(A\)를
이 된다.
참고문헌
[Lee] 이인석, 선형대수와 군, 서울대학교 출판문화원, 2005.
-
미적분학의 기본정리, 대수학의 기본정리 등등과는 달리 선형대수학의 기본정리는 저자에 따라 전혀 다른 정리들을 의미하기도 한다. 예를 들어 [Goc]에서는 이전 글에서의 rank-nullity 정리를, Gilbert Strang의 경우 다음 글에서 다룰 직교여공간에 대한 정리들을 선형대수학의 기본정리라고 부른다. 우리는 [Lee]를 따라 이 정리를 선형대수학의 기본정리라 부르기로 한다. ↩
댓글남기기