앞선 글에서 우리는 벡터공간 $V$의 쌍대공간 $V^\ast$를 정의하고, 만일 $V$가 유한차원이라면 $V^\ast$의 쌍대공간인 $V^{\ast\ast}$와 $V$가 isomorphic하다는 것을 살펴봤다. 이 과정에서 핵심적으로 쓰인 사실은 non-degenerate pairing $\langle -,-\rangle:V\times W \rightarrow \mathbb{K}$가 $V$에서 $W^\ast$, 그리고 $W$에서 $V^\ast$로의 단사인 linear map을 정의한다는 것이었다. 우리는 이 사실을 canonical pairing
\[\langle -,-\rangle:V\times V^\ast\rightarrow \mathbb{K};\quad (v,f)\mapsto f(v)\]에 적용하고, 차원을 고려하여 $V$와 $V^{\ast\ast}$가 isomorphic하다는 것을 살펴보았다. 이렇게 유도되는 $V\rightarrow V^{\ast\ast}$를 기술하기 위해서는 $V$에서 basis를 선택할 필요가 없었다.
한편, 우리는 이전 글의 서두에서 $V$와 $V^\ast$ 또한 같은 차원을 갖는다는 것을 언급하였는데, 이는 위의 자연스러운 isomorphism $V\rightarrow V^{\ast\ast}$와는 다르게 특정한 basis $\{x_1,\ldots, x_n\}$을 택한 후, 이들의 dual basis $\{\xi^1,\ldots, \xi^n\}$을 택하여 $x_i\mapsto \xi^i$를 통해 정의해야 한다는 차이가 있었다.
쌍선형형식
이제 우리는 $V=W$인 경우에 집중한다.
정의 1 임의의 pairing $\langle -,-\rangle:V\times W\rightarrow \mathbb{K}$에 대하여, 만일 $W=V$라면 이 pairing을 $V$ 위에서 정의된 bilinear form쌍선형형식이라 부른다. $\langle -,-\rangle$이 non-degenerate bilinear form비퇴화 쌍선형형식이라는 것은 $\langle-,-\rangle$이 pairing으로서 non-degenerate인 것이다.
$V$ 위에 bilinear form이 주어졌다 하자. 그럼 위와 같은 논증을 통해, 우리는 $V$에서 $V^\ast$로의 linear map들
\[v\mapsto \langle v,-\rangle,\qquad v\mapsto \langle -,v\rangle\]을 얻는다. 일반적으로 이 둘은 같을 필요가 없지만, 다음을 정의할 수 있다.
정의 2 임의의 bilinear form $\langle-,-\rangle:V\times V\rightarrow \mathbb{K}$에 대하여, 다음의 식
\[\langle v,w\rangle=\langle w,v\rangle\]이 모든 $v,w\in V$에 대해 성립하면 이 form이 symmetric대칭적이라 말한다. 만일 모든 $v,w\in V$에 대해 다음의 식
\[\langle v,w\rangle=-\langle w,v\rangle\]이 성립하면 이 form이 alternating교대적이라 말한다.
비퇴화 쌍선형형식
유한차원 $\mathbb{K}$-벡터공간 $V$가 주어졌다 하고, 앞서 언급한 canonical pairing $\langle-,-\rangle:V\times V^\ast\rightarrow \mathbb{K}$을 생각하자. 만일 $V$ 위에 non-degenerate pairing $\langle -,-\rangle:V\times V\rightarrow \mathbb{K}$가 주어졌다면, 우리는 §쌍대공간, ⁋따름정리 5로부터 $\langle -,-\rangle$이 isomorphism
\[V\rightarrow V^\ast;\qquad v\mapsto \langle -,v\rangle\tag{1}\]을 정의한다는 것을 안다.
편의를 위해 앞으로는 $\langle -,-\rangle$이 처음부터 symmetric non-degenerate bilinear form이었던 것으로 가정하자. 그럼 $\langle -,-\rangle$는 식 (1)에 의해 정의된 isomorphism을 가지며, 이는 다음과 같이 쓸 수 있다.
따름정리 3 Symmetric non-degenerate bilinear form $\langle -,-\rangle$이 주어진 유한차원 $\mathbb{K}$-벡터공간 $V$를 생각하자. 임의의 $f\in V^\ast$가 주어질 때마다, 적당한 $w\in V$가 유일하게 존재하여
\[f(v)=\langle v,w\rangle\qquad\text{for all $v\in V$}\]이 성립한다.
그럼 특히 이전 글에서 정의한 orthogonal complement의 개념을 $V$로 가져올 수 있다. 즉, 다음과 같이 정의하자.
정의 4 Symmetric non-degenerate bilinear form $\langle -,-\rangle$이 주어진 유한차원 $\mathbb{K}$-벡터공간 $V$를 생각하자. 임의의 $v\in V$에 대하여, 다음의 식 $\langle w,v\rangle=0$을 만족하는 모든 $w\in V$들의 모임을 $v$의 orthogonal complement직교여공간이라 하고, $v^\perp$로 적는다. 더 일반적으로, 임의의 집합 $S$에 대하여, 다음 집합
\[S^\perp=\bigcap_{v\in S}v^\perp\]을 $S$의 orthogonal complement로 정의한다.
물론, 만일 $\langle -,-\rangle$이 symmetric하지 않았더라도 동일한 정의를 할 수 있으며, 실제로 $v$를 $\langle -,v\rangle$로 보내는지 혹은 $\langle v,-\rangle$으로 보내는지를 선택한 후 이 선택을 꾸준히 유지한다면 동일한 결과를 얻게 된다. 어쨌든 혹시 모를 혼란을 피하기 위해 우리는 $\langle -,-\rangle$이 symmetric이라는 조건을 유지한다.
벡터 $w\in V$는 따름정리 3에 의해 $f\in V^\ast$를 유일하게 지정하는데, 위의 정의는 만일 이렇게 얻어진 $f$가 §쌍대공간, ⁋정의 7의 의미에서 $v$의 orthogonal complement라면, $w$를 $v$에 직교하는 것으로 생각하고, 이러한 $w$들을 모아둔 것을 orthogonal complement로 생각하겠다는 의미이다. 이러한 과정을 통해 §쌍대공간의 결과들을 모두 $V$로 가져올 수 있다. 남은 글에서 우리는 이 과정을 자세히 살펴본다.
우선 두 유한차원 $\mathbb{K}$-벡터공간 $V,W$ 위에 symmetric non-degnerate bilinear form $\langle -,-\rangle_V$와 $\langle -,-\rangle_W$가 주어졌다 하자. 또, 논의의 편의를 위하여 이들 bilinear form에 의해 결정되는 isomorphism들을 각각
\[\varphi_V:V^\ast\rightarrow V,\qquad \varphi_W:W^\ast\rightarrow W\]으로 적자.
만일 $V,W$ 위에 각각 두 basis $\mathcal{B}=\{x_1,\ldots, x_n\}$과 $\mathcal{C}=\{y_1,\ldots, y_m\}$이 주어졌다면, dual basis
\[\mathcal{B}^\ast=\{\xi^1,\ldots, \xi^n\},\qquad\mathcal{C}^\ast=\{\upsilon^1,\ldots,\upsilon^m\}\]들이 잘 정의된다. 이제 이들을 $\varphi_V,\varphi_W$를 따라 옮긴 basis
\[\mathcal{B}'=\{\varphi_V(\xi^1),\ldots,\varphi_V(\xi^n)\},\qquad\mathcal{C}'=\{\varphi_W(\upsilon^1),\ldots,\varphi_W(\upsilon^m)\}\]를 생각하자. 즉 이들은 다음의 식
\[\langle x_i,\varphi_V(\xi^j)\rangle=\delta_{ij},\qquad\langle y_i,\varphi_W(\upsilon^j)\rangle=\delta_{ij}\]을 통해 정의되는 $V,W$의 원소들이다. 이제 임의의 $L:V\rightarrow W$에 대하여,
\[\begin{aligned}L(x_1)&=\alpha_{11}y_1+\alpha_{21}y_2+\cdots+\alpha_{m1}y_m\\L(x_2)&=\alpha_{12}y_1+\alpha_{22}y_2+\cdots+\alpha_{m2}y_m\\&\phantom{a}\vdots\\L(x_n)&=\alpha_{1n}y_1+\alpha_{2n}y_2+\cdots+\alpha_{mn}y_m\end{aligned}\]이라 하자. 만일 dual map $L^\ast:W^\ast\rightarrow V^\ast$를 위의 identification $\varphi$들을 통해 $W$에서 $V$로의 map으로 생각한다면, 즉 다음의 diagram
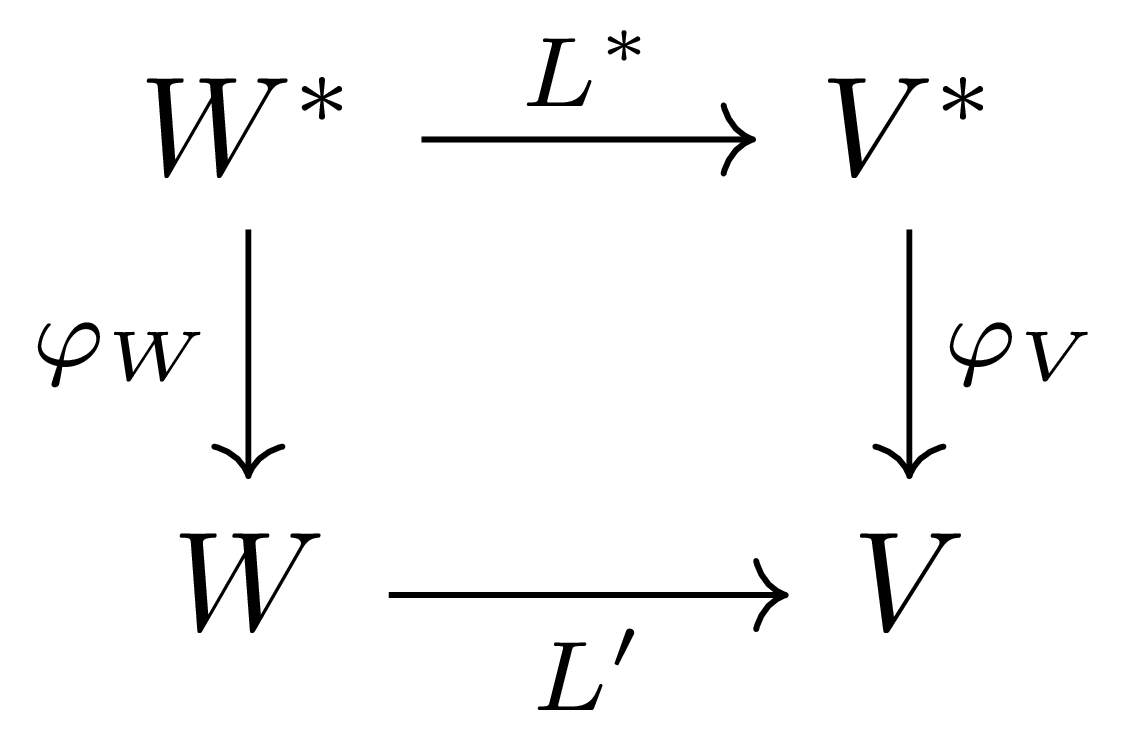
을 통해 정의되는 $L’:W\rightarrow V$를 생각한다면 이 linear map의 두 basis $\mathcal{C}’$, $\mathcal{B}’$에 대한 행렬표현이 $[L’]_{\mathcal{B}’}^{\mathcal{C}’}$가 됨을 확인할 수 있다.
한편, 이렇게 정의한 $L’:W\rightarrow V$는 다음 식
\[\langle Lv, w\rangle_W=\langle v,L'w\rangle_V\qquad\text{for all $v\in V$ and $w\in W$}\tag{1}\]을 만족하는 것을 알 수 있다. 이는
\[\langle Lv,w\rangle=(\varphi^{-1}(w))(Lv)=(\varphi^{-1}_W(w)\circ L)(v)=(L^\ast(\varphi^{-1}_W(w))(v)=(\varphi^{-1}_V(v)\circ L')(w)=(\varphi^{-1}_V(v))(L'w)=\langle v,L'w\rangle\]으로부터 확인할 수 있다. 이러한 식을 만족하는 $L’$을 우리는 linear map $L$의 adjoint라 부르고, 약간의 abuse of notation을 통해 $L^\ast$으로 적기도 한다.
§쌍대공간, §§직교여공간의 결과들은 모두 canonical pairing에 대한 식 $(Lv,f)=(v,L^\ast f)$로부터 얻어졌다. 따라서, 이를 위에서 얻은 non-degenerate bilinear form $\langle -,-\rangle$들에 대한 식 (1)로 대체하면 다음 결과들을 얻는다.
명제 5 Symmetric non-degnerate bilinear form들이 주어진 두 $\mathbb{K}$-벡터공간 $V,W$, linear map $L:V\rightarrow W$와 그 adjoint $L^\ast:W\rightarrow V$가 주어졌다 하자. 그럼
- 임의의 부분공간 $U\subseteq V$에 대하여, $L(U)^\perp=(L^\ast)^{-1}(U^\perp)$가 성립한다.
- 임의의 부분공간 $U\subseteq W$에 대하여, $L^\ast(U)^\perp=L^{-1}(U^\perp)$가 성립한다.
- $(\im L)^\perp=\ker(L^\ast)$이 성립한다.
- $(\im L^\ast)^\perp=\ker L$이 성립한다.
특히, 3번과 4번에서 얻어지는 $V$와 $W$의 부분공간들
\[\ker L, \quad(\ker L)^\perp, \quad\im L,\quad(\im L)^\perp\]를 $L$에 의해 결정되는 네 개의 기본공간들four fundamental subspaces이라 부르기도 한다. 특히 이들은
\[V=\ker L\oplus(\ker L)^\perp,\qquad W=\im L\oplus(\im L)^\perp\]를 만족한다.
직교기저
이제 symmetric non-degenerate bilinear form이 주어진 $\mathbb{K}$-벡터공간 $V$를 생각하자. 그럼 $V$의 부분집합 $\{v_1,\ldots, v_n\}$이 orthogonal set이라는 것은 $i\neq j$일 때마다 $\langle v_i,v_j\rangle=0$이 성립하는 것이다. 만일 $V$의 basis $\mathcal{B}$가 orthogonal set이기도 하다면, 이를 orthogonal basis라 부른다.
정의 6 Field $\mathbb{K}$가 다음의 조건
\[\underbrace{1+1+\cdots+1}_\text{$p$ times}=0\]을 만족한다면 $\mathbb{K}$의 characteristic표수이 $p$라고 하고 이를 $\ch \mathbb{K}=p$로 표기한다. 만일 위의 식을 만족하는 자연수 $p$가 존재하지 않는다면 $\mathbb{K}$는 characteristic 0을 갖는 것으로 생각한다.
예를 들어 $\mathbb{R}$은 characteristic 0을 갖는다. 만일 $\mathbb{F}_2=\{0,1\}$에 다음의 식
\[0+0=0,\quad 0+1=1,\quad 1+0=1,\quad 1+1=2\]그리고
\[0\cdot 0=0,\quad 0\cdot 1=0,\quad 1\cdot 0=0,\quad 1\cdot 1=1\]으로 덧셈과 곱셈을 각각 정의한다면 $\mathbb{F}_2$는 field의 조건을 만족한다는 것을 확인할 수 있고, 이 때 $\ch\mathbb{F}_2=2$이다.
명제 7 $\ch \mathbb{K}\neq 2$인 field $\mathbb{K}$에 대하여, symmetric non-degenerate bilinear form이 주어진 $\mathbb{K}$-벡터공간 $V$는 항상 orthogonal basis를 갖는다.
증명
우선 간단한 보조정리를 보이자. 임의로 고정된 $v\in V$에 대하여, 반드시 $\langle u,v\rangle\neq 0$이도록 하는 $u\in V$가 존재한다. 그럼
\[2\langle u,v\rangle=\langle u+v,u+v\rangle-\langle u,u\rangle-\langle v,v\rangle\]이고, 두 조건 $\langle u,v\rangle\neq 0$과 $\ch \mathbb{K}\neq 2$에서 좌변은 0이 아니다. 따라서 우변의 세 항 $\langle u+v,u+v\rangle, \langle u,u\rangle,\langle v,v\rangle$ 가운데 적어도 하나는 0이 아니다. 따라서,
Non-degnerate symmetric bilinear form이 주어진 임의의 $\mathbb{K}$-벡터공간에는 $\langle w,w\rangle\neq 0$을 만족하는 $w$가 반드시 존재한다.
원래의 명제는 $V$의 차원에 대한 귀납법으로 증명한다. $\dim V=0$인 경우는 증명할 것이 없다. 이제 $\dim V=k$인 경우 증명이 완료되었다 가정하자. 그럼 $\dim V=k+1$를 만족하는 임의의 벡터공간 $V$에 대하여, $\langle w,w\rangle\neq 0$을 만족하는 벡터 $w$가 존재한다.
이제 $W=\span w$라 하고 $W^\perp$를 생각하자. 그럼 임의의 $v\in V$에 대하여, 다음의 식
\[v=\frac{\langle v,w\rangle}{\langle w,w\rangle}w+\left(v-\frac{\langle v,w\rangle}{\langle w,w\rangle}w\right)\]으로부터 $V$의 임의의 원소는 $W$와 $W^\perp$의 원소의 합으로 표현할 수 있다는 것을 안다. 또, 가정에 의해 $\langle w,w\rangle\neq 0$이므로 $W\cap W^\perp=\{0\}$이 성립한다. 따라서 §벡터공간의 차원, ⁋예시 8에 의하여
\[k+1=\dim V=\dim(W+W^\perp)=\dim W+\dim W^\perp-\dim(W\cap W^\perp)\]으로부터 $\dim W^\perp=k$임을 안다. 뿐만 아니라, 임의의 $v\in W^\perp$에 대하여, $\langle u,v\rangle\neq 0$을 만족하는 $u$에 대하여,
\[u'=u-\frac{\langle u,w\rangle}{\langle w,w\rangle}w\in W^\perp\]는 $W^\perp$의 원소이며,
\[\langle u',v\rangle=\langle u,v\rangle\neq 0\]을 만족한다. 즉, $W^\perp$ 또한 $\langle-,-\rangle$에 대해 non-degenerate이며, 따라서 귀납적 가정에 의해 $W^\perp$에는 orthogonal basis $\mathcal{B}$가 존재한다. 이제 $\mathcal{B}\cup\{v\}$는 $V$의 orthogonal basis이므로, 원하는 결과를 얻는다.
Gram matrix
임의의 bilinear form $\langle-,-\rangle:V\times V\rightarrow \mathbb{K}$가 주어졌다 하자. 만일 $V$의 basis $\{x_1,\ldots, x_n\}$가 고정되었다고 하면, 임의의 $v=\sum v_ix_i, w=\sum w_jx_j$에 대하여 다음의 식
\[\langle v,w\rangle=\left\langle\sum_{i=1}^nv_ix_i,\sum_{j=1}^n w_jx_j\right\rangle=\sum_{i,j=1}^n v_iw_j\langle x_i,x_j\rangle\]이 성립한다. 잠시 $(i,j)$ 성분이 $\langle x_i,x_j\rangle$인 $n\times n$ 행렬을 $G$라 표기하면, 위 식은
\[\langle v,w\rangle=v^t Gw\]으로 간단하게 쓸 수 있다. 이 때 $G$를 basis $\mathcal{B}$에 대한 Gram matrix라 부른다.
$V$ 위에 주어진 두 basis $\mathcal{B},\mathcal{C}$를 생각하자. 이들에 대한 Gram matrix를 각각 $G_\mathcal{B},G_\mathcal{C}$로 표현하고 위의 식을 정확하게 적으면,
\[\langle v,w\rangle=[v]^t_\mathcal{B}G_\mathcal{B}[w]_\mathcal{B}=[v]^t_\mathcal{C}G_\mathcal{C}[w]_\mathcal{C}\]라 할 수 있다. 이제 $[v]_\mathcal{C}=[\id]_\mathcal{C}^\mathcal{B}[v]_\mathcal{B}$이므로, 위의 식의 가장 우변은
\[[v]_\mathcal{C}^tG_\mathcal{C}[w]_\mathcal{C}=\left([\id]_\mathcal{C}^\mathcal{B}[v]_\mathcal{B}\right)^tG_\mathcal{B}\left([\id]_\mathcal{C}^\mathcal{B}[w]_\mathcal{B}\right)=[v]_\mathcal{B}^t\left(([\id]_\mathcal{C}^\mathcal{B})^t G_\mathcal{B}[\id]_\mathcal{C}^\mathcal{B}\right)[w]_\mathcal{B}\]이 된다.
[Lee] 이인석, 선형대수와 군, 서울대학교 출판문화원, 2005.
[Goc] M.S. Gockenbach, Finite-dimensional linear algebra, Discrete Mathematics and its applications, Taylor&Francis, 2011.

댓글남기기