행렬식

지금까지 우리의 관심은 주로 벡터공간과 linear map에 집중되어 있었다. 그러나 선형대수학의 기본정리로부터 linear map은 사실 행렬과 동일한 것임을 알게 되었고, 이에 우리는 행렬을 본격적으로 탐구하는 선형대수학의 두 번째 파트를 시작한다.

행렬식의 정의

행렬을 살펴볼 때 가장 기본이 되는 도구는 행렬식이다. 행렬식은 $n$차 정사각행렬 $A$에 대응되는 스칼라 $\det A$이며, 대수적으로 행렬식은 그 값이 $0$인지 아닌지에 따라 $A^{-1}$의 존재 여부를 결정해주는 실수로 볼 수 있다. 행렬식을 계산하는 방법에는 여러가지가 있고, 이들 중 일부는 정의로 받아들여지기도 하지만 이들 중 어떤 것도 행렬식의 본질적인 의미를 담지 못한다. 우리는 우선 행렬식을 올바르게 정의한 후, 이에 대한 존재성을 증명하는 과정에서 행렬식의 계산을 소개한다.

행렬식은 $\Mat_n(\mathbb{k})$에서 $\mathbb{k}$로의 함수이다. 이제 $\Mat_n(\mathbb{k})$의 각 행렬들을 $\mathbb{k}^n$에 속하는 $n$개의 벡터들의 모임으로 생각하면 행렬식은 $(\mathbb{k}^n)^n$, 즉 벡터공간 $\mathbb{k}^n$을 $n$개 곱한 공간에서 $\mathbb{k}$로의 함수가 된다. 따라서 임의의 행렬 $A\in\Mat_n(\mathbb{k})$에 대하여, 우리는 $A$의 행렬식을 $\det(A)$로도 표기하고, 동시에 $A$의 열벡터들을 이용해 $\det(A_1,\ldots, A_n)$으로 표기하기도 한다. 이는 곧 두 $n^2$차원 $\mathbb{k}$-벡터공간 $\Mat_n(\mathbb{k})$와 $(\mathbb{k}^n)^n\cong \mathbb{k}^{n^2}$을 다음의 isomorphism

\[A=(A_1\;A_2\;\cdots\;A_n)\cong (A_1, A_2, \cdots, A_n)\cong \bigl((A_{11}, A_{21}, \ldots, A_{n1}), (A_{12},A_{22},\ldots, A_{n2}),\ldots, (A_{1n},A_{2n},\ldots, A_{nn})\bigr)\]

을 통해 동일하게 취급하는 것과 같다.

정의 1 $\mathbb{k}$-벡터공간 $V,W$에 대하여, 다음의 함수

\[f:\underbrace{V\times\cdots\times V}_\text{ {\footnotesize $n$} times}\rightarrow W\]

가 multilinear map_{다중선형사상}이라는 것은 $f$가 각각의 성분에 대해 linear인 것이다.

특별히 $n=2$인 경우, $f$를 bilinear하다고 부른다. (§쌍대공간, ⁋정의 1)

정의 2 두 $\mathbb{k}$-벡터공간 $V,W$와 multilinear map

\[f: \underbrace{V\times\cdots\times V}_\text{ {\footnotesize $n$} times}\rightarrow W\]

이 주어졌다 하자. 만일 임의의 $v_1,\ldots, v_n$와 임의의 $i\neq j$에 대해 항상 다음의 식

\[f(v_1,\ldots, v_i, \ldots, v_j,\ldots, v_n)=-f(v_1,\ldots, v_j,\ldots, v_i,\ldots, v_n)\]

이 성립한다면 $f$를 alternating multilinear map_{교대다중선형사상}이라 부른다.

위와 같이 multilinear map $f:V\times\cdots\times V\rightarrow W$이 주어졌다 하자. 그럼 $f$가 antisymmetric이라는 것은 임의의 $v_1,\ldots, v_n$와 임의의 $i\neq j$에 대하여, 만일 $v_i=v_j$이면 $f(v_1,\ldots, v_n)=0$인 것이다.

명제 3 Multilinear map $f:V\times\cdots\times V\rightarrow W$가 alternating인 것은 $f$가 antisymmetric인 것과 동치이다.

증명

우선 $f$가 alternating이라 가정하자. 그럼 임의의 $v_i=v_j$를 만족하는 임의의 $v_1,\ldots, v_n\in V$에 대하여

\[\begin{aligned}f(v_1,\ldots,v_i,\ldots, v_j,\ldots, v_n)&=f(v_1\ldots, v_j,\ldots,v_i,\ldots, v_n)\\&=-f(v_1,\ldots, v_i,\ldots, v_j,\ldots, v_n)\end{aligned}\]

이 성립하므로 $f$는 antisymmetric이기도 하다. (첫째 등식은 $v_i=v_j$라는 사실을, 둘째 등식은 $f$가 alternating이라는 사실을 사용하였다.)

거꾸로 $f$가 antisymmetric이라 하자. 임의의 $v_1,\ldots, v_n$과 임의의 $i\neq j$에 대하여, $f$가 antisymmetric이라는 사실은 다음의 식

\[f(v_1,\ldots, v_i+v_j,\ldots, v_i+v_j,\ldots, v_n)=0\]

을 준다. 여기서 $v_i+v_j$는 각각 $i,j$번째 성분에 들어있다. 이제 multilinearity를 적용하면 위 식은

\[\begin{aligned}0&=f(v_1,\ldots, v_i,\ldots, v_i,\ldots, v_n)+f(v_1,\ldots, v_i,\ldots, v_j,\ldots,v_n)\\&\phantom{==}+f(v_1,\ldots, v_j,\ldots, v_i,\ldots,v_n)+f(v_1,\ldots, v_j,\ldots, v_j,\ldots, v_n)\end{aligned}\]

이 되고, 다시 $f$는 antisymmetric이므로 $v_i, v_j$가 각각 두 번 나오는 첫째 항, 마지막 항이 $0$이 된다. 이로부터 원하는 결론을 얻는다.

특히, $f$가 변수 $n$개의 alternating linear map이고 $v_1,\ldots, v_n$ 중 하나가 다른 $n-1$개의 벡터들의 일차결합이라 가정하자. 그럼 multilinearity를 적용한 후, 위의 명제를 적용하면 $f(v_1,\ldots, v_n)=0$임을 알 수 있다.

이제 우리는 행렬식을 정의할 수 있게 되었다.

정의 4 $D(e_1,\ldots, e_n)=1$을 만족하는 alternating multilinear map $D:(\mathbb{k}^n)^n\rightarrow \mathbb{k}$를 행렬식_determinant이라 부른다.

우리는 아직 행렬식이 존재한다는 것도, 유일하다는 것도 보이지 않았기에 $\det$ 대신 $D$라는 표기를 사용했다. 다음 글에서 행렬식의 계산을 소개하며 이를 증명하고, 이후부터 표준적인 표기법 $\det$를 사용한다.

넓이와 부피

평행사변형의 넓이는 밑변의 길이에 높이를 구한 값으로 주어진다. 이와 비슷하게 평행육면체의 부피는 밑면의 넓이에 높이를 구한 값으로 주어진다. 어렵지 않게 이를 고차원으로 일반화시키는 것 또한 가능할 것이다. 편의상 4차원 이상의 도형에 대한 초부피 또한 간단하게 부피로 통칭한다.

위의 정의 또한 마찬가지로 해당 도형들의 넓이를 구하는 하나의 방법일 뿐이다. 넓이와 부피에 대한 올바른 정의를 하는 것이 행렬식에 기하학적 의미를 부여해준다.

$n$차원 공간에서 일차독립인 $n$개의 벡터가 주어졌다 하자. 그럼 이들은 $n$차원의 입방체를 만들게 된다. 가령 $n=3$인 경우, 세 개의 벡터 $v_1,v_2,v_3$은 다음과 같이 평행육면체를 만든다.

서술의 편의상 앞으로의 내용은 모두 2차원 상에서의 넓이를 이용해 설명하지만, 어렵지 않게 이 내용들을 모두 $n$차원 공간으로 일반화할 수 있다.

우선 우리는 어떠한 평행사변형이 단위넓이 1을 갖는지를 정의해야 한다. 물론 여기에는 많은 선택의 여지가 있으나, 가장 합리적인 방법은 한 변의 길이가 1인 정사각형을 단위넓이 1을 갖는 평행사변형으로 정의하는 것이다.

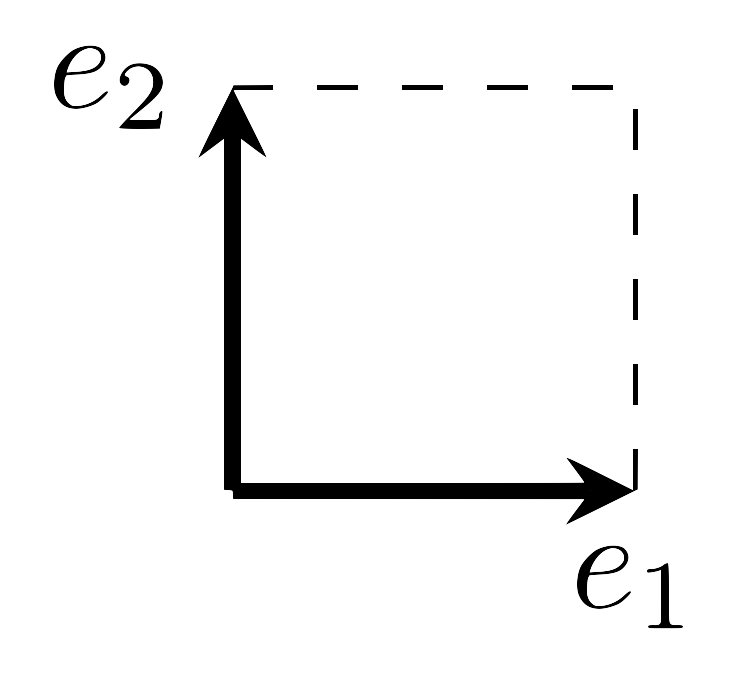
한편, 위의 정사각형에서 출발하여 다음의 두 규칙을 적용하면 모든¹ 평행사변형을 만들 수 있다는 것이 명확하다.

1. 등적변형: 평행사변형의 한 변을 고정하고, 남은 한 변의 끝점을 고정한 한 변의 방향으로 평행이동하는 변형.
2. 한 변은 고정된 상태로, 남은 한 변의 길이를 $k>0$배 하는 변형.

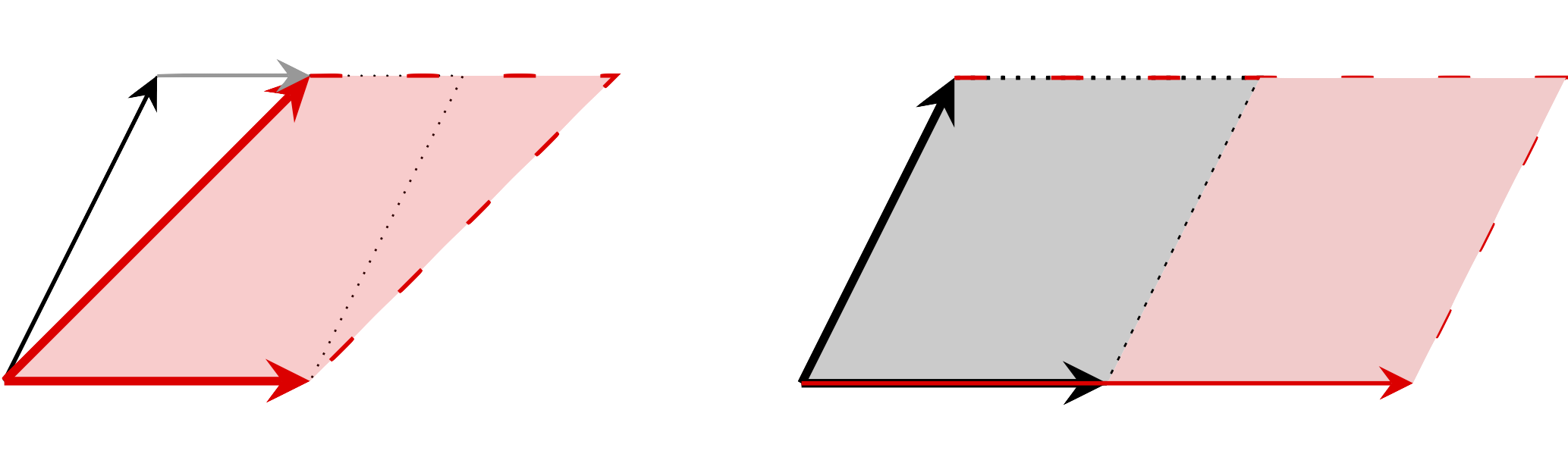
따라서 1번과 2번 각각의 규칙을 따라 평행사변형을 변형하였을 때, 넓이가 어떻게 변형되는지만 정의한다면 모든 평행사변형의 넓이를 정의하는 것이 된다. 1번의 경우, 우리는 넓이가 변하지 않는 것으로 정의하고, 2번의 경우 넓이가 $k$배가 된 것으로 정의한다. 이렇게 정의한다면 모든 평행사변형의 넓이는 우리가 기존에 알던 평행사변형의 넓이와 동일해진다.²

행렬식의 기하학적 의미

행렬식에 기하학적 직관을 불어넣기 위해, 이 절에서는 $\mathbb{k}=\mathbb{R}$인 것으로 생각한다.

$D$가 음의 부호를 가질 수 있다는 사실만 제외한다면, $D$를 넓이함수로 볼 수 있다. 이 때 $D$의 부호는 방향을 의미한다.

우선 $D$가 만족해야 할 첫 번째 조건, 즉 단위정사각형의 넓이는 1이라는 조건은 행렬식의 정의 $D(e_1,\ldots, e_n)=1$로부터 얻어진다.

일반적인 넓이의 개념에서는 평행사변형의 한 변의 길이를 $-1$배 하여도 넓이가 양수가 된다. 그러나 이 도형을 원래 도형과 반대되는 방향을 갖는 것으로 생각한다면 넓이를 음수로 볼 수도 있고, 그럼 $D$가 한 변의 길이의 임의의 스칼라배를 보존한다는 것을 확인할 수 있으며, 등적변형을 생각하면 $D$는 다음과 같이 한 변에 해당하는 두 벡터를 더한 결과 또한 보존한다.

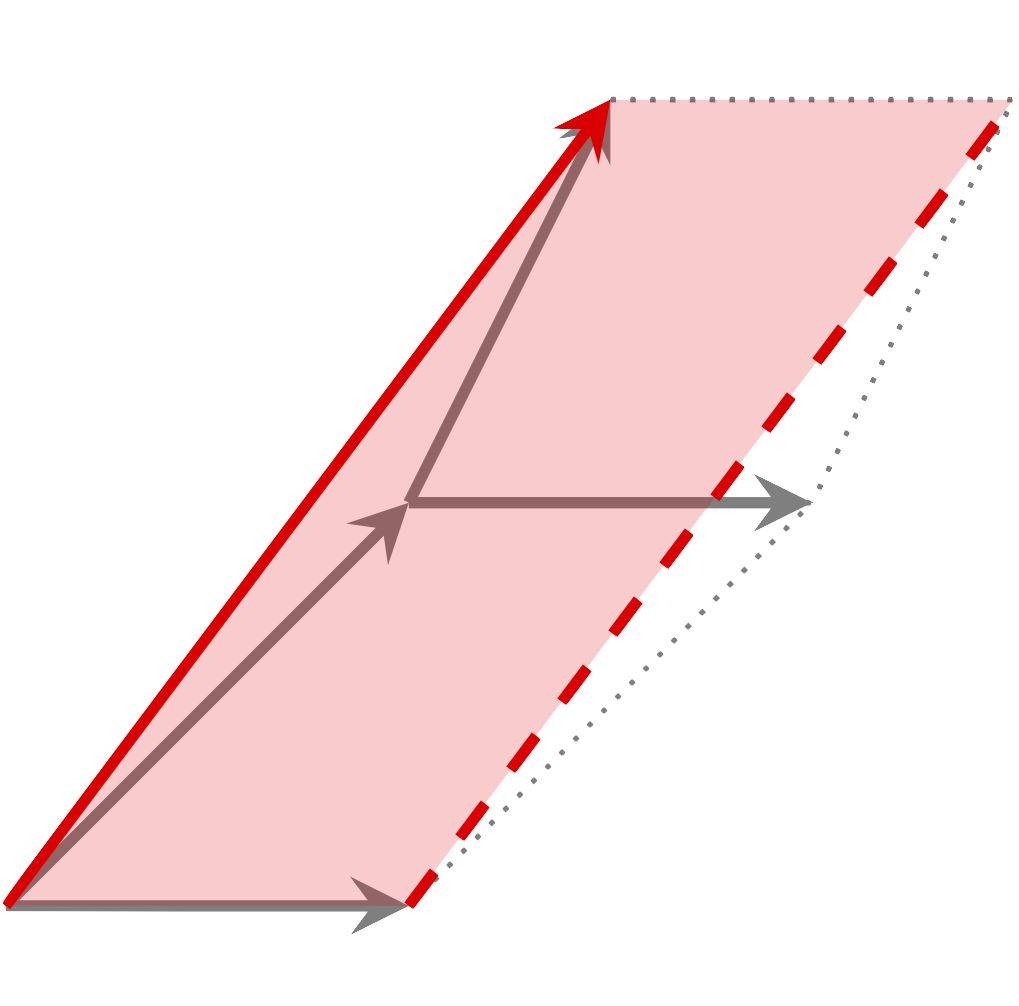
뿐만 아니라, 등적변형을 생각하면 고정된 한 변 $v_n$에 대하여, 밑면을 이루는 $n-1$개의 벡터 $v_1,\ldots, v_{n-1}$의 일차결합을 $v_n$에 더하여도 $D$의 값은 유지된다. 이는 곧, 만일 $v_n$이 $v_1,\ldots, v_{n-1}$의 일차결합이라면 $D(v_1,\ldots, v_n)=0$이라는 것이고 따라서 명제 3에 의해 이는 $D$가 alternating이라는 것과 동치가 된다.

우리는 아직 행렬식의 유일성을 증명하지 않았지만, 정의 4는 행렬식을 완전하게 결정해준다는 것을 확인할 수 있고, 따라서 행렬식을 부호가 있는 부피로 생각할 수 있다. 이제 이 그림 상에서, 행렬식이 $0$인 것과 $A$가 가역이 아닌 것이 동치인 이유는 $n$차원 공간에서, $n$차원 미만의 나란히꼴의 부피는 항상 0이기 때문임을 알 수 있다.

다음 글에서는 실제로 행렬식이 유일하게 존재한다는 것을 보인다. 이를 통해 행렬식의 여러 계산방법을 알게 된다.

---

참고문헌

[Goc] M.S. Gockenbach, Finite-dimensional linear algebra, Discrete Mathematics and its applications, Taylor&Francis, 2011.

---

1. 합동인 평행사변형은 동일한 것으로 취급한다. ↩

2. 엄밀히 말하자면, 넓이가 잘 정의된 것인지는 확인하지 않았다. 예를 들어 단위 정사각형에서 1, 2번 과정을 통해 주어진 평행사변형을 만드는 방법이 여러가지가 있다 하더라도 위와 같이 정의된 넓이가 동일한지를 확인해보아야 한다. 이는 직관에 맡기고 넘어가기로 한다. ↩