푸앵카레 쌍대성

이번 글에서 우리는 대수적 위상수학의 아름다운 정리인 푸앵카레 쌍대성에 대해 다룬다. 이전 글에서 언급한 것과 같이, 푸앵카레 쌍대성은 호몰로지와 코호몰로지 사이의 쌍대성을 보여준다. 우리가 이미 살펴본 universal coefficient theorem (§코호몰로지, ⁋정리 5)의 경우, $C^\bullet(X;A)$를 $C_\bullet(X;A)$의 dual로서 정의했을 때 어느정도 예상 가능한 결과였지만 푸앵카레 쌍대성은 보다 더 기하학적인 의미를 가지고 있다.

방향층

푸앵카레 쌍대성을 정의하기 위해서는 우선 방향의 개념을 정의해야 한다. 이는 topological manifold (§위상다양체, ⁋정의 2) 위에서 정의되는 개념으로, 이번 글에서는 별다른 말이 없다면 임의의 manifold는 connected인 것으로 가정한다.

임의의 topological manifold $M$ of dimension $m$과 열린집합 $U$를 생각하면, 다음의 대응

\[U\mapsto H_m(M, M\setminus U;\mathbb{Z})\]

은 임의의 $U\subseteq V$에 대하여 자연스러운 restriction map

\[H_m(M, M\setminus V;\mathbb{Z})\rightarrow H_m(M,M\setminus U;\mathbb{Z})\tag{1}\]

을 가지므로 presheaf이다.

정의 1 대응 (1)의 sheafification ([위상수학] §층, ⁋정의 5)을 orientation sheaf_방향층라 부르고 $\or_M$로 적는다.

그럼 임의의 $x\in M$와 $x$의 임의의 열린근방 $U$에 대하여, 다음의 canonical map

\[H_m(M,M\setminus U;\mathbb{Z})\rightarrow H_m(M,M\setminus\{x\};\mathbb{Z})\]

이 존재한다. 이들은 위의 restriction map에 대해 잘 행동하며, 따라서 direct limit의 map

\[\or_{M,x}=\varinjlim_{x\in U} H_m(M,M\setminus U;\mathbb{Z})\rightarrow H_m(M,M\setminus \{x\};\mathbb{Z})\]

이 잘 정의된다.

정의에 의하여 $H_m(M,M\setminus{x};\mathbb{Z})$의 원소는 $m$-simplex $\sigma:\Delta^m \rightarrow M$ 중 그 boundary가 $x$와 만나지 않는 것들이며, 그럼 우리는 충분히 작은 $x$의 근방 $U$를 택해 이 boundary가 $U$와 만나지 않도록 할 수 있다. 한편, 만일 두 homology class $\alpha_U\in H_m(M,M\setminus U;\mathbb{Z})$, $\alpha_V\in H_m(M,M\setminus V;\mathbb{Z})$가 $H_m(M,M\setminus {x};\mathbb{Z})$에서 같은 원소라면 마찬가지로 이 두 원소의 boundary와 모두 만나지 않는 $x$의 충분히 작은 열린근방 $W$를 찾을 수 있고, 그럼 $\alpha_U$와 $\alpha_V$는 $H_m(M,M\setminus W;\mathbb{Z})$에서는 같은 원소여야 한다. 즉 위의 함수

\[\varinjlim_{x\in U}H_m(M,M\setminus U;\mathbb{Z})\rightarrow H_m(M,M\setminus \{x\};\mathbb{Z})\]

는 isomorphism이다. 한편 §호몰로지의 계산, ⁋정리 2에 의하여

\[H_m(M,M\setminus\{x\};\mathbb{Z})\cong H_m(U,U\setminus\{x\};\mathbb{Z})\cong H_m(\mathbb{R}^m, \mathbb{R}^m\setminus\{0\};\mathbb{Z})\]

이고, $\mathbb{R}^m\setminus{0}$은 $S^{m-1}$으로 deformation retract하므로 relative homology long exact sequence에 의하여 위의 식의 우변은 $\mathbb{Z}$와 isomorphic한 것을 알 수 있으며, 이 sheaf는 locally constant sheaf인 것 또한 확인할 수 있다. 즉, 임의의 $x\in M$이 주어질 때마다 적당한 열린근방 $U$가 존재하여 $\or_M\vert_U$가 constant sheaf이도록 할 수 있다. ([위상수학] §층, ⁋예시 9)

정의 2 Relative homology group $H_m(M, M\setminus \{x\};\mathbb{Z})$을 $M$의 $x$에서의 local homology group이라 부른다.

상수층과 피복공간, 방향생성자층

위에서 정의한 orientation sheaf $\or_M$에 대해 자세히 살펴보기 위해서는 constant sheaf와 locally constant sheaf를 조금 더 자세히 살펴볼 필요가 있다. 우선 임의의 abelian group $A$를 생각하고, 여기에 discrete topology를 주어 이를 위상공간으로 생각하자. 그럼 위상공간 사이의 projection map $X\times A \rightarrow X$는 trivial covering space이며, 이 covering map의 section들의 sheaf가 바로 constant sheaf $\underline{A}$이다. 거꾸로 constant sheaf $\underline{A}$가 주어질 경우, 우리는 $\underline{A}$의 étale space $\Spe(\underline{A})$가 covering space $X\times A \rightarrow X$가 된다는 것을 확인할 수 있다. ([위상수학] §준층, ⁋정의 9) 그럼 locally constant sheaf는 별다른 것이 아니라 그 étale space가 covering space가 되는 sheaf인 것을 알 수 있다.

직관적으로 $H_m(M,M\setminus\{x\};\mathbb{Z})\cong \mathbb{Z}$는 $x$를 그 interior에 포함하는 $m$-simplex $\sigma:\Delta^m\rightarrow M$가 $x$를 몇 번 덮는지를 알려준다. 한편 $\Delta^m$은 꼭짓점이 어떻게 순서가 부여되었는지에 따라 부호를 줄 수 있고, 그럼 이 isomorphism을 통해 이러한 $m$-simplex들에 $\mathbb{Z}$의 원소를 대응시켰을 때 두 $m$-simplex의 부호 차이는 두 $m$-simplex의 source $\Delta^m$가 반대방향으로 부호가 매겨진 것, 혹은 $\Delta^m$의 부호를 하나로 고정했을 때 두 simplex map이 다른 방향을 지정하는 것으로 생각할 수 있다. 즉 $H_m(M,M\setminus\{x\};\mathbb{Z})$는 점 $x$에서의 orientation에 대한 정보를 담고 있다.

그렇다면 자연스러운 질문은, 모든 점 $x\in M$마다 orientation을 잘 정하여, 이들 orientation이 $M$ 위의 global한 orientation과 일치하도록 이어붙일 수 있는지의 여부일 것이다. 이를 위해서는 우선 reference 역할을 할 $\mathbb{Z}$가 필요하다. 이를 위해 $M$ 위에 constant sheaf $\underline{\mathbb{Z}}$를 하나 고정하자. ([위상수학] §준층, ⁋예시 6) 그럼 각각의 $x\in M$에 대하여 그 stalk $\underline{\mathbb{Z}}_x$은 generator $1$이 consistent한 방식으로 선택되어 있는 것으로 생각할 수 있고, 따라서 각각의 $x$에 대하여 isomorphism

\[\Iso_\mathbb{Z}(H_m(M, M\setminus\{x\}), \underline{\mathbb{Z}}_x)\]

을 선택하는 것은 각각의 $x$에서 $M$이 양의 방향인지, 음의 방향인지를 택하는 것과 같다.

정의 3 Topological manifold $M$ of dimension $m$에 대하여, 점 $x$에서의 local orientation_{국소 방향}은 $\Iso_\mathbb{Z}(H_m(M,M\setminus\{x\}), \underline{\mathbb{Z}}_x)$의 원소를 택하는 것으로 주어진다.

이제 각각의 열린집합 $U$에 대하여

\[\omega_M^\pre(U)=\prod_{x\in U}\Iso_\mathbb{Z}(H_m(M,M\setminus\{x\}), \underline{\mathbb{Z}}_x)\]

으로 정의하고, $U\subseteq V$일 때마다 $\rho_{VU}:\omega_M^\pre(V)\rightarrow \omega_M^\pre(U)$를 canonical projection으로 정의하자. ([집합론] §곱집합의 성질, ⁋정의 1) 그럼 $\omega_M^\pre$은 $M$ 위에 정의된 presheaf가 되며 ([위상수학] §준층, ⁋정의 4), 각각의 $p\in M$에 대하여 $\omega_M^\pre$의 점 $x$에서의 stalk $\omega_{M,x}^\pre$는 $\{\pm 1\}$이 된다. ([위상수학] §준층, ⁋정의 9)

이제 $\omega_M^\pre$의 sheafification $\omega_M$을 $M$의 orientation-generator sheaf_{방향생성자층}라 부른다. 이는, 방향이 고정된 constant sheaf $\underline{\mathbb{Z}}$의 generator $1$을 고정해뒀을 때, isomorphism $H_m(M,M\setminus\{x\};\mathbb{Z})$이 $1$을 $1$로 보내는지, $-1$로 보내는지 살펴보는 것이며 이를 통해 $\omega_M$은 $\or_M$의 subsheaf로 볼 수 있다. 그럼 $\omega_M$은 locally constant sheaf이므로, 그 étale space $\Spe(\omega_M)$는 $M$의 covering space가 되며 각 fiber는 두 개의 원소로 이루어져 있다.

정의 4 위에서 정의한 étale space $\Spe(\omega_M)$을 $M$의 orientation double cover_{방향 이중덮개}라 부르고, global section $M \rightarrow \Spe(\omega_M)$을 global orientation_{전역 방향}이라 부른다. $M$이 orientable_가향이라는 것은 global orientation이 존재하는 것이다.

그럼 그 이름과 같이 $\Spe(\omega_M)$은 $M$의 covering space이며, 뿐만 아니라 임의의 $x\in M$에 대하여, $x$의 chart $U$를 생각하면 canonical projection $p:\Spe(\omega_M)\rightarrow M$에 의한 $U$의 preimage $p^{-1}(U)$가 $U$와 homeomorphic한 두 개의 disjoint open subset으로 나타난다.

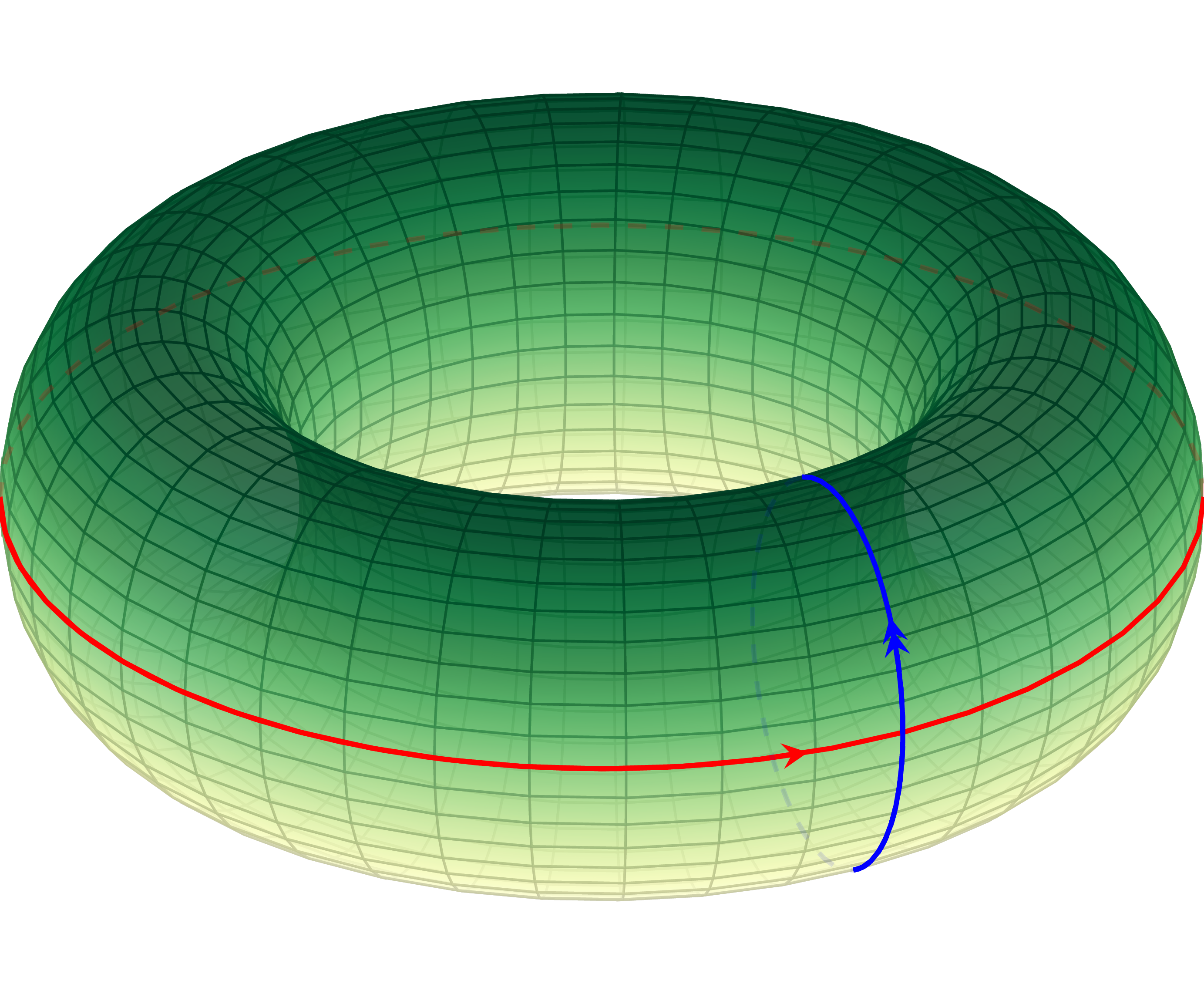
예시 5 예를 들어 $S^1$의 orientation double cover $p:\Spe(\omega_{S^1})\rightarrow S^1$을 생각하자. 임의의 점 $x\in S^1$의 $p$에 의한 preimage $p^{-1}(x)$는 두 개의 점 $(p,+)$와 $(p,-)$로 이루어져 있으며, 이는 $x$를 포함하는 chart $U$에 대해서도 마찬가지가 되어 $p^{-1}(U)$가 두 개의 open subset $U^+,U^-$로 나뉘게 된다.

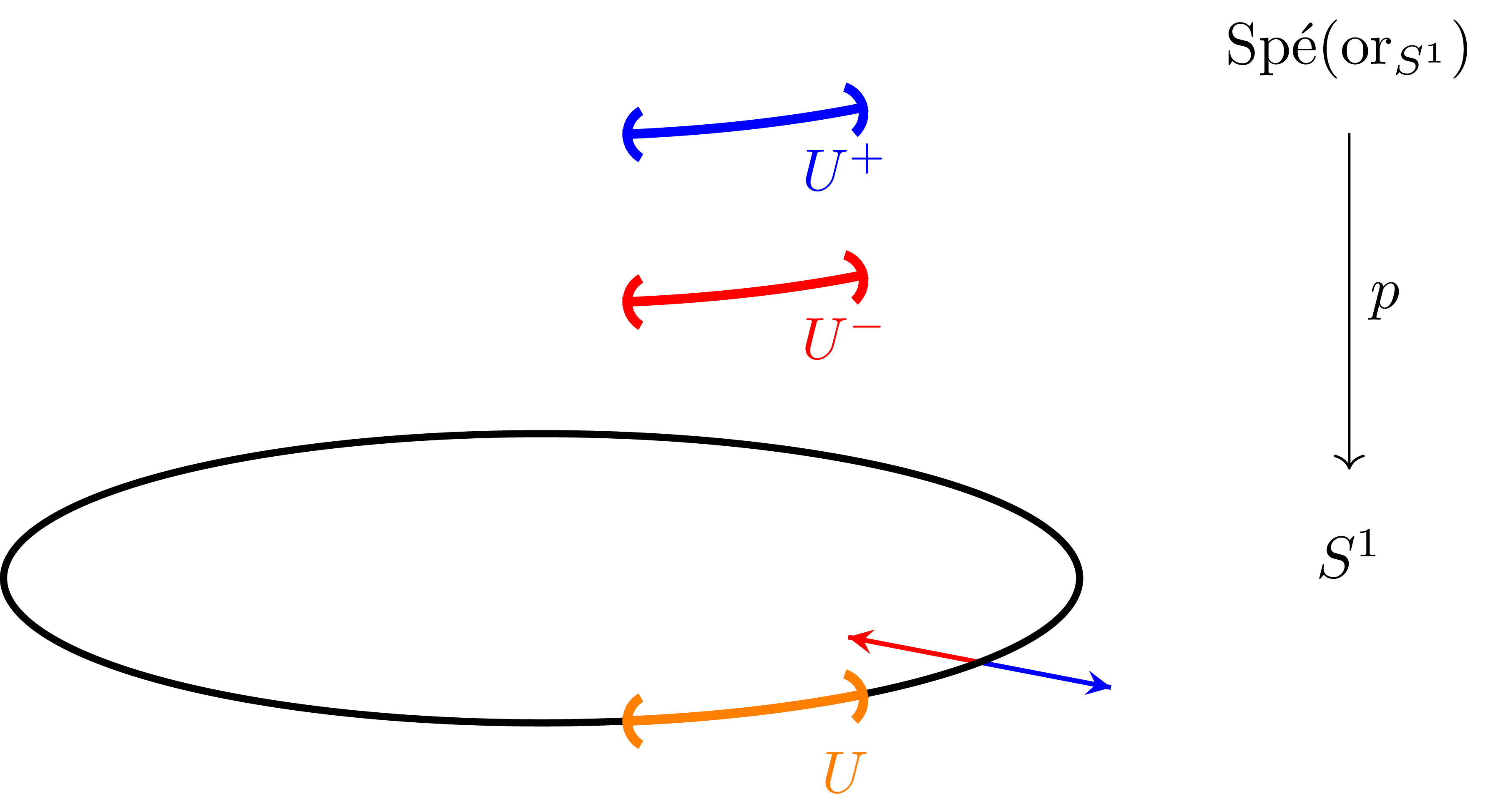
이제 $S^1$을 이러한 cover들로 덮어주면, 각각의 chart들이 겹치는 곳에서 orientation을 그대로 붙여주면 이들은 다음과 같이 두 개의 component를 갖는 double cover가 된다.

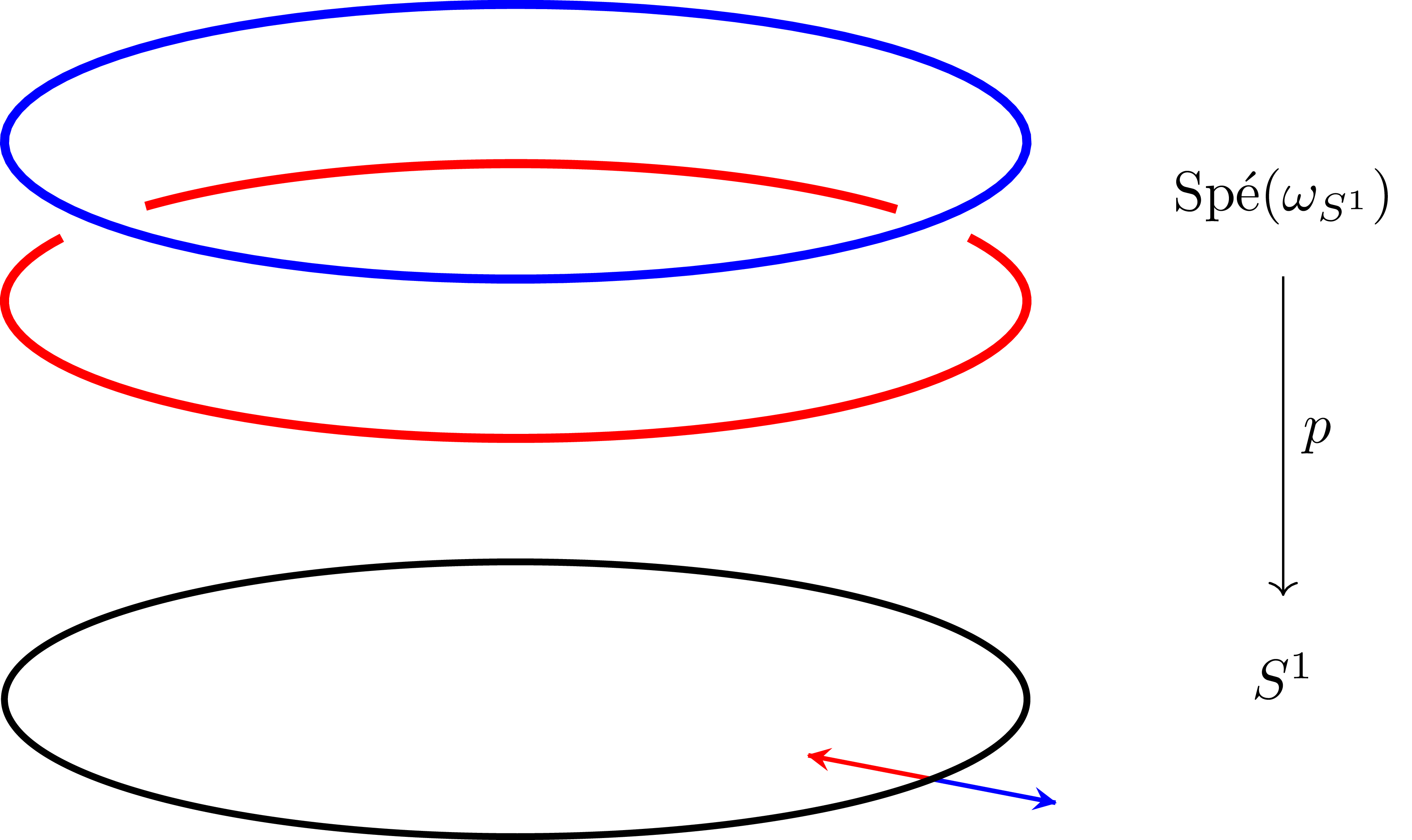
그러나 임의의 double cover가 항상 trivial cover가 되는 것은 아니다. 예를 들어 위의 $S^1$의 cover에서 위쪽과 아래쪽 component를 교차해서 붙이면 component가 하나인 double cover를 얻게 되며, 비슷한 일이 non-orientable manifold의 orientation double cover에서 일어난다.

이를 관찰하기 위해 뫼비우스 띠 $M$의 orientation cover를 생각하자. $S^1$과 마찬가지로, 임의의 점 $x\in M$에 대하여 $p^{-1}(x)$는 두 개의 점 $(x,+)$와 $(x,-)$로 이루어지며 이는 $M$의 임의의 점에 대해서도 마찬가지이다.

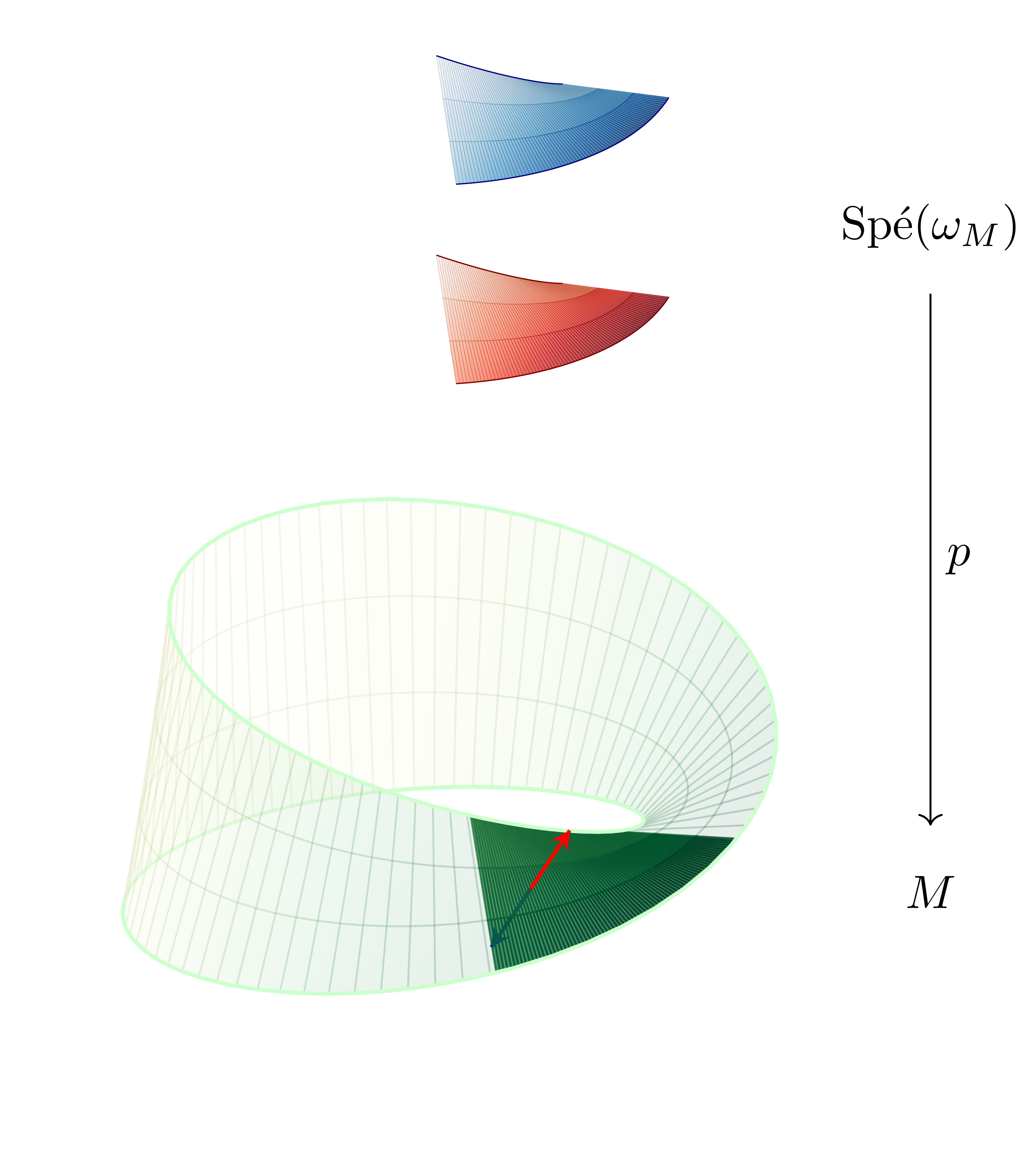
그러나 이를 이어붙여 $M$ 전체를 이어붙이려 하면 문제가 생기는데, 이 그림에서 보여지는 두 개의 cover를, orientation을 고려해가며 반시계방향으로 붙여나가면, 다시 $x$로 돌아왔을 때 $(x,+)$와 $(x,-)$가 서로 뒤바뀌어 있으므로 위쪽과 아래쪽 component를 교차해서 붙여야 한다. 이렇게 만들어진 $M$의 double cover는 원기둥과 homeomorphic하게 된다.

정의에 의해 $M$이 orientable이려면 $\omega_M$의 global section이 존재하며, 이는 $\Spe(\omega_M)$이 trivial covering space라는 것과 동치이며 이는 다시 $\omega_M$이 constant sheaf라는 것과 동치이다. 여기에 §피복공간, ⁋정리 12를 적용하면 다음 명제를 얻는다.

명제 6 (Connected) topological manifold $M$에 대하여, 다음이 동치이다.

1. $M$이 orientable이다.
2. $\Spe(\omega_M)$이 두 개의 component를 갖는다.
3. $\pi_1(M)$의 monodromy action이 $\Spe(\omega_M)$에서 trivial하게 act한다.

그런데 우리는 이미 호몰로지와 코호몰로지를 다룰 때 $\mathbb{Z}$-module뿐 아니라, 일반적인 $A$-module로 확장했으므로 위의 논증 또한 일반적인 $A$-module에 대해 확장할 수 있다. 이를 위해 우선 [대수적 위상수학] §코호몰로지, ⁋명제 1의 relative homology 버전을 생각하면, 다음의 (non-canonical) isomorphism

\[H_k(M, M\setminus\{x\};A)\cong H_k(M,M\setminus\{x\})\otimes_\mathbb{Z}A\oplus\Tor_1^\mathbb{Z}(H_{k-1}(M, M\setminus\{x\}), A)\]

가 존재하는 것을 관찰하자. 그런데 $H_k(M,M\setminus \{x\})$는 $k\neq m$인 경우는 항상 trivial group이므로, 이 isomorphism으로부터 우리는

\[H_m(M,M\setminus \{x\};A)\cong H_m(M,M\setminus\{x\})\otimes_\mathbb{Z}A\cong A\]

임을 안다. 따라서 위의 논증에서 등장하는 $\mathbb{Z}$를 모두 $A$로 바꾸어도 말이 될 것이며, 특히 우리는 $A$-orientation들의 presheaf

\[\omega_M^A(U)=\prod_{x\in U}\Iso_A(H_m(M,M\setminus\{x\};A), \underline{A}_x)\]

그리고 이로부터 정의되는 global $A$-orientation의 개념을 얻을 것이다. 이렇게 얻어지는 $A$-orientation sheaf $\omega_M^A$는 별다른 것이 아니라 $\omega_M\otimes A$에 불과하다.

이 정의에서 명제 6과 같은 결과를 도출하기 위해 §피복공간, ⁋정리 11를 다시 살펴보자. 우리는 각각의 covering space $p:E \rightarrow M$에 대하여, fiber $p^{-1}(x)$ 위에 monodromy functor가 정의하는 $\pi_1(M,x)$-action을 생각하였고, 이는 곧 group homomorphism $\pi_1(M,x)\rightarrow \Aut(p^{-1}(x))$를 생각하는 것과 같았다. 그렇다면 covering space $p:\Spe(\omega_M)\rightarrow M$에 대하여 $\pi_1(M,x)$-action은 어떻게 정의되는지를 살펴보아야 하는데, 이 때 fiber $p^{-1}(x)$는 stalk $\mathbb{Z}$의 automorphism

\[\Iso_\mathbb{Z}(\mathbb{Z},\mathbb{Z})\cong \mathbb{Z}^\times\cong \{\pm 1\}\]

으로부터 정의되는 것이고 따라서 $\pi_1(M,x)$-action은 정확하게 group homomorphism $\pi_1(M,x)\rightarrow \mathbb{Z}^\times$로 생각할 수 있다. 그럼 $A$에서 $A$로의 $A$-module isomorphism은 정확히 $A$의 unit group $A^\times$의 원소와 대응되므로, 이는 결과적으로 group homomorphism $\pi_1(M,x)\rightarrow A^\times$를 살펴보는 것과 같다. 즉 명제 6은 다음과 같이 일반화할 수 있다.

명제 7 (Connected) topological manifold $M$에 대하여, 다음이 동치이다.

1. $M$이 $A$-orientable이다.
2. $\Spe(\omega_M^A)$이 trivial covering $M\times \lvert A^\times\rvert$이다.
3. Monodromy representation $\pi_1(M)\rightarrow A^\times$는 trivial이다.

이러한 일반화에서 가장 특기할만한 경우는 $A=\mathbb{Z}/2$일 때이다. 이 경우, $A$의 unit은 $-1=1$ 뿐이므로 orientation을 지정하는 방법은 유일하고, 따라서 임의의 manifold는 항상 $\mathbb{Z}/2$-orientable이다.

기본류

이제 우리는 global ($A$-)orientation의 존재성에 대해 살펴본다. 즉, 모든 $x\in X$에 대하여 local orientation들 $s_x$이 주어졌을 때, 적당한 global section $s:M\rightarrow \Spe(\omega_M^A)$이 존재하여 $s(x)=(x,s_x)$이도록 할 수 있는지를 살펴볼 것이다.

한편 우리는 다음의 canonical homomorphism

\[H_m(M; A)\rightarrow H_m(M,M\setminus\{x\};A)\tag{1}\]

을 통해, 임의의 top homology class $\alpha\in H_m(M;A)$는 local homology group의 원소 $\alpha_x\in H_m(M,M\setminus\{x\};A)$를 정의하는 것을 안다. 그렇다면 자연스러운 질문 중 하나는 각각의 $x\in S_x$마다 주어진 local orientation $s_x$들을 $A^\times$의 원소로 보아 이를 $H_m(M,M\setminus{x};A)$의 원소로 취급했을 때, 모든 $x\in X$에 대하여 $\alpha\in H_m(M;A)$의 $H_m(M,M\setminus\{x\};A)$에서의 image가 $s_x$이도록 할 수 있는 $\alpha$가 존재하는지의 여부일 것이다.

위의 두 문단은 푸앵카레 쌍대성이 어떠한 꼴인지를 보여준다. Global section $s:M \rightarrow \Spe(\omega_M^A)$는 본질적으로 $M$ 전체 위에 정의된 함수로서, $0$번째 cohomology에 해당하는 개념이다. 반면 $\alpha\in H_m(M;A)$는 $m$번째 homology의 원소이다. 푸앵카레 쌍대성은 이들 두 개념이 동치라는 것과, 더 일반적으로, $k$번째 cohomology와 $n-k$번째 homology 사이의 duality를 보여준다.

이제 남은 글에서 우리가 해야 할 것은 크게 두 가지이다.

1. Canonical homomorphism (1)의 lifting이 global orientation을 정의하고, 그 반대도 성립한다는 것을 보인다.
2. Global orientation $M \rightarrow \Spe(\omega_M^A)$가 존재하는 sheaf cohomology를 정의한다.

푸앵카레 쌍대성의 핵심적인 내용은 모두 첫째 단계에 담겨있는 것이며, 둘째 단계는 이를 현명하게 표현할 수 있는 언어를 배우는 것에 가깝다. 따라서 우리는 우선 첫째 단계부터 시작한다. 이는 다음의 보조정리에 의해 얻어진다.

보조정리 8 Topological manifold $M$ of dimension $m$을 고정하자. $M$의 임의의 compact subset $C$에 대하여 다음이 성립한다.

1. 임의의 section $s:M \rightarrow \Spe(\omega_M^A)$가 주어질 때마다, 적당한 homology class

   \[\alpha_C\in H_m(M,M\setminus C;A)\]

   이 유일하게 존재하여, 임의의 $x\in C$마다 canonical homomorphism

   \[H_m(M,M\setminus C;A)\rightarrow H_m(M,M\setminus\{x\};A)\]

   에 의한 $\alpha_C$의 image가 $s_x$이도록 할 수 있다.

2. 모든 $i>n$에 대해 $H_i(M, M\setminus C;A)=0$이다.

증명

우선 임의의 compact set $C_1,C_2$, 그리고 이들의 교집합 $C_1\cap C_2$에 대해 이 명제가 성립한다면 $C_1\cup C_2$에 대해서도 명제가 성립함을 보이자. 이는 Mayer-Vietoris sequence

\[\cdots \rightarrow H_k(M,M\setminus (C_1\cup C_2); A)\rightarrow H_k(M,M\setminus C_1;A)\oplus H_k(M,M\setminus C_2;A)\rightarrow H_k(M, M\setminus (C_1\cap C_2);A)\rightarrow\cdots\tag{2}\]

에서, $k>m$에 대해서는 귀납적 가정에 의해

\[H_k(M,M\setminus C_1;A)=H_k(M,M\setminus C_2;A)=H_k(M,M\setminus(C_1\cap C_2);A)=0\]

이므로 $H_k(M,M\setminus (C_1\cup C_2);A)$ 또한 $0$이어야 하고, 이로부터 둘째 주장이 성립한다.

첫째 주장을 보이기 위해 section $s:M \rightarrow \Spe(\omega_M^A)$이 주어졌다 하자. 귀납적 가정에 의해 이들은 $C_1,C_2,C_1\cap C_2$에 대해서는 lifting이 가능하므로, 이들을 이어붙여 $C_1\cup C_2$에 대하여 class $\alpha_{C_1\cup C_2}$를 만들어야 한다. 이들 $\alpha_{C_1},\alpha_{C_2},\alpha_{C_1\cap C_2}$의 유일성에 의하여 $\alpha_{C_1}$과 $\alpha_{C_2}$는 모두 $\alpha_{C_1\cap C_2}$에서 같은 원소가 되어야 하므로, (2)에서 원소

\[(\alpha_{C_1},-\alpha_{C_2})\in H_m(M,M\setminus C_1;A)\oplus H_m(M,M\setminus C_2;A)\]

를 생각하면 이 원소는 $H_m(M,M\setminus C_1;A)\oplus H_m(M,M\setminus C_2;A)\rightarrow H_m(M, M\setminus (C_1\cap C_2);A)$의 kernel에 속하고, 따라서 $H_m(M,M\setminus (C_1\cup C_2);A)$의 원소를 택할 수 있고 유일성은

\[0=H_{m+1}(M,M\setminus (C_1\cap C_2);A)\rightarrow H_m(M,M\setminus (C_1\cup C_2))\rightarrow H_m(M,M\setminus C_1;A)\oplus H_m(M,M\setminus C_2;A)\]

의 injectivity로부터 나온다.

이제 귀납법의 기초단계를 위해서는 $M=\mathbb{R}^m$이고 $A$가 convex compact subset인 경우를 생각하면 충분하다. 임의의 manifold $M$의 compact set을 Euclidean chart로 덮은 후, compactness를 사용하면 $M=\mathbb{R}^m$으로 가정해도 충분하며 $\mathbb{R}^m$의 open ball들의 basis를 사용하고 다시 compactness를 사용하면 $A$가 convex임을 추가로 가정해도 되기 때문이다. 그럼 이 단계에서 두 공간 $\mathbb{R}^m\setminus A$와 $\mathbb{R}^m\setminus \{x\}$가 모두 같은 공간 $S^{m-1}$로 deformation retract하므로 isomorphism이 되고, 이로부터 증명이 끝난다.

이 증명에서 compactness는 Mayer-Vietoris sequence를 사용하여 귀납적인 방식으로 $\alpha$를 구성할 때, 이 귀납적인 과정이 유한한 단계에서 끝나도록 하려면 반드시 필요하다. 실제로 compactness가 빠질 경우 푸앵카레 쌍대성은 다소 다른 형태를 띄게 되는데, 이를 공통된 식으로 표현하기 위해 도입해야 하는 것이 sheaf cohomology의 언어이다.

어쨌든 위의 보조정리 8에 의하여, 만일 $M$이 compact topological manifold of dimension $m$이라면, $C=M$으로 두어 다음의 정리를 얻는다.

정리 9 Compact connected topological manifold $M$ of dimension $m$이 주어졌다 하자. 그럼 orientation sheaf $\omega_M^A$이 주어질 때마다 적당한 class $[M]\in H_m(M;A)$이 유일하게 존재하여 canonical homomorphism (1)에 의한 $[M]$의 image가 $s_x$와 일치하도록 할 수 있다.

그럼 보조정리 8에 의하여 $H_m(M;A)$는 $[M]$에 의해 생성되는 free $A$-module of rank 1이며, 서로 다른 global orientation의 선택은 서로 다른 $H_m(M;A)$의 generator의 선택에 대응된다.

정의 10 위의 정리 9에서 정의한 $[M]$을 global orientation $s$가 정의하는 $M$의 fundamental class_기본류라 부른다.

뿐만 아니라, 만일 정리 9의 조건을 만족하는 homology class $[M]$이 존재한다면, 이로부터 global section $s:M \rightarrow \Spe(\omega_M^A)$이 주어진다는 것을 안다.

푸앵카레 쌍대성

이제 주어진 manifold가 $A$-orientable일 경우의 푸앵카레 정리를 증명할 수 있다. 이를 위해 다음의 cap product homomorphism

\[-\frown -: H^p(M;A)\otimes_A H_m(M;A) \rightarrow H_{m-p}(M;A)\]

을 생각하자. 그럼 $H_m(M;A)\cong A$이므로, 이 homomorphism은 $H^p(M;A)$에서 $H_{m-p}(M;A)$로의 $A$-module homomorphism이라 생각할 수 있다. 특히 $H_m(M;A)$의 generator $[M]$을 도입하면, 이는 다음의 homomorphism

\[-\frown [M]: H^p(M;A)\rightarrow H_{m-p}(M;A)\]

이 된다.

정리 11 $A$-orientable compact manifold $M$ of dimension $m$과 그 fundamental class $[M]$에 대하여, 위의 homomorphism

\[-\frown [M]: H^p(M;A)\rightarrow H_{m-p}(M;A)\]

은 isomorphism이다.

이에 대한 증명 또한 보조정리 8의 증명과 마찬가지로 Mayer-Vietoris sequence를 이용한 귀납법으로 진행한다. 그러나 다소 다른 점은, 보조정리 8은 명제의 주장이 compact subset $C$에 대한 주장이어서 compactness를 적극적으로 사용할 수 있었지만, 이번에는 명제가 $M$ 자체에 대한 주장이기 때문에, 가령 $M$의 chart $U$가 주어졌다고 하면 이는 compact가 아니므로 단순한 귀납법으로 접근할 수는 없다. 이에 우리는 다음을 정의한다.

정의 12 Cochain $\varphi\in C^p(M;A)$이 compactly supported라는 것은 적당한 compact set $K\subseteq M$이 존재하여 $\varphi(\sigma)=0$가 $M\setminus K$에 들어가는 모든 simplex에 대해 성립하는 것을 말한다. Compactly supported cochain들의 cochain complex의 $i$번째 호몰로지를 $p$번째 compactly supported cohomology라 부르고 $H_c^p(M;A)$로 적는다.

그럼 다음의 식

\[H_c^p(M;A)\cong \varinjlim_{\text{\scriptsize$K$ compact}}H^p(M,M\setminus K;A)\]

이 성립하는 것이 직관적으로도 자명하며 증명도 명확하다. 각각의 compact set $K$에 대하여,

\[H^p(M,M\setminus K;A)\rightarrow H_c^p(M;A)\]

가 canonical하게 존재하며, 이것이 우변의 directed system과 호환되어 homomorphism

\[\varinjlim_{\text{\scriptsize$K$ compact}}H^p(M,M\setminus K;A)\rightarrow H_c^p(M;A)\]

이 잘 정의되기 때문이다. 이것이 isomorphism인 것은 직접 보이면 된다. 특히 임의의 compact manifold $M$에 대하여 $H_c^p(M,A)\cong H^p(M;A)$이 성립하며, 따라서 원하는 결과는 다음의 보조정리에서 따라나온다.

보조정리 13 임의의 $A$-orientable $m$-manifold $M$에 대하여 다음의 isomorphism

\[H_c^p(M;A)\cong H_{m-p}(M;A)\]

이 모든 $p$에 대하여 성립한다.

증명

이를 위해서는 우선 isomorphism을 정의해야 한다. 이를 위해, 임의의 compact subset $K$에 대하여 cap product

\[H^p(M,M\setminus K;A)\times H_m(M,M\setminus K;A)\rightarrow H_{m-p}(M;A)\]

을 생각하자. 그럼 보조정리 8에 의하여, 우리는 각각의 point $x$로 제한했을 때 $M$의 orientation $x$와 맞아떨어지는 homology class

\[s_K\in H_m(M,M\setminus K;A)\]

를 찾을 수 있다. 우리의 주장은 이러한 $s_K$들로 만드는 cap product homomorphism

\[-\frown s_K: H^p(M,M\setminus K;A) \rightarrow H_{m-p}(M;A)\]

이 direct system에 대한 compatibility를 만족하고, 따라서 homomorphism $H_c^p(M;A)\rightarrow H_{m-p}(M;A)$을 정의한다는 것이다. 이를 확인하기 위해 $K$를 포함하는 또 다른 compact subset $K’$와 inclusion $i:K\rightarrow K’$이 주어졌다 하자. 그럼 임의의 $\alpha\in H^p(M,M\setminus K;A)$에 대하여,

\[i^\ast\alpha\frown s_{K'}=\alpha\frown i_\ast s_{K'}\]

가 projection formula(§합곱, ⁋명제 6)에 의해 성립하며, 보조정리 8의 유일성에 의하여 $i_\ast s_{K’}=s_K$이므로 이것이 homomorphism $H_c^p(M;A)\rightarrow H_{n-p}(M;A)$을 잘 정의하는 것을 안다.

우리 주장은 이 homomorphism $D_M:H_c^p(M;A)\rightarrow H_{n-p}(M;A)$이 isomorphism이라는 것이며, 이를 보이기 위해 보조정리 8의 증명과 마찬가지로 Mayer-Vietoris sequence를 이용한 귀납법을 사용한다.

귀납법의 base step은 $M=\mathbb{R}^m$인 경우이다. 이 경우, 우리는 임의의 ball $B\subseteq \mathbb{R}^m$에 대하여, $B$의 orientation $s_B$가

\[H_m(\mathbb{R}^m, \mathbb{R}^m\setminus B;A)\cong A\]

을 주는 것을 알고, §코호몰로지, ⁋명제 3으로부터 $H^m(\mathbb{R}^m,\mathbb{R}^m\setminus B;A)\cong A$이며, 이 때 $B$의 orientation의 dual basis에 해당하는 $\alpha_B$가 다음의 식

\[\langle 1\smile \alpha_B, s_B\rangle=\langle 1,\alpha_B\frown s_B\rangle\]

을 만족하므로 $\alpha_B\frown s_B$가 $H_0(\mathbb{R}^m)\cong A$의 generator에 해당하는 것을 알고, 따라서

\[H^p(\mathbb{R}^m,\mathbb{R}^m\setminus B;A)\cong H_{m-p}(\mathbb{R}^m;A)\]

이 모든 $p$에 대해 성립한다. ($p\neq m$인 경우는 zero module 사이의 zero map이므로 isomorphism이다.) 이제 $B$의 반지름을 키워가며 $\mathbb{R}^m$ 전체를 덮는 directed system을 짜면 $H_c^p(M)\rightarrow H_{m-p}(M)$이 isomorphism임을 안다.

이제 다음 스텝으로, 만일 $M$의 두 열린집합 $U,V$가 존재하여 $M=U\cap V$이고 주어진 명제가 $U,V,U\cap V$에 대해 성립한다 가정하자. 그럼 각각의 compact subset $K\subset U$, $L\subset V$에 대하여 relative Mayer-Vietoris sequence

\[\cdots\rightarrow H^k(M,M\setminus(K\cap L);A)\rightarrow H^k(M,M\setminus K;A)\oplus H^k(M,M\setminus L;A)\rightarrow H^k(M,M\setminus(K\cup L);A)\rightarrow \cdots\]

를 생각한 후, excision을 하고 limit을 취하면 다음의 commutative diagram

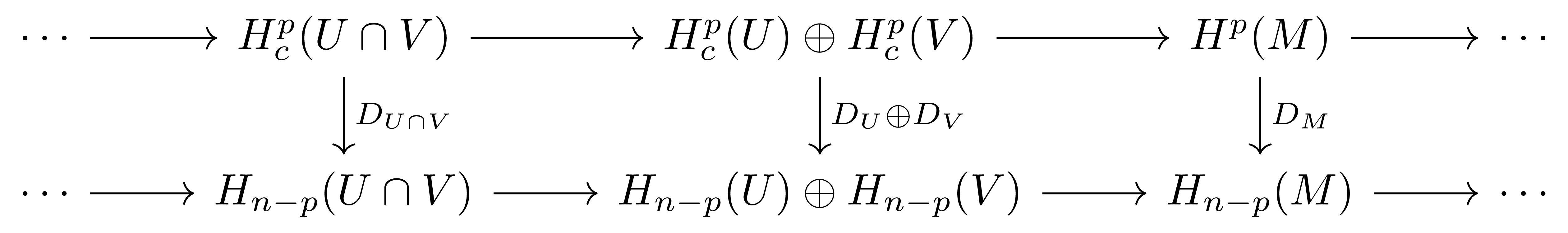
을 얻고, 귀납적 과정과 [호몰로지 대수학] §Diagram chasing, ⁋정리 2로부터 귀납법이 완성된다.

그러나 $M$이 compact라는 가정이 없으므로 약간의 논증을 덧붙여야 한다. 우선 만일 $M$이 open subset들의 nested family

\[U_1\subset U_2\subset\cdots\]

의 union이고 이들 각각에 대하여 주어진 명제가 성립한다 하자. 그럼 $M$의 임의의 compact subset은 어떠한 $U_i$에는 반드시 포함되어야 하고, 이로부터 다음의 isomorphism

\[H_c^p(M)=\varinjlim_i H^p_c(U_i),\qquad H_{m-p}(M)=\varinjlim_i H_{m-p}(U_i)\]

을 얻는다. 가정에 의하여 $H^p_c(U_i)\rightarrow H_{m-p}(U_i)$들이 모두 isomorphism이므로 원하는 결과를 얻는다.

이제 $M$이 $\mathbb{R}^m$의 open subset안 경우를 생각하자. 그럼 우선 $M$을 $\mathbb{R}^m$과 homeomorphic한 convex open subset들 (즉 open ball들) counbable개 $U_1,U_2,\ldots$로 덮을 수 있으며, 임의의 convex open subset은 $\mathbb{R}^m$과 homeomorphic하므로 이들 각각에 대해서는 정리의 isomorphism이 성립함을 위의 base step에서 보았다. 또, convex set 두 개의 교집합은 다시 convex set이므로, 위의 귀납법에 의하여 $U_1\cup U_2$에 대해서도 결론이 성립한다. 이 다음 차례로 $U_1\cup U_2\cup U_3$에 대하여 결론이 성립하는 것을 보이기 위해서는 다음의 교집합

\[(U_1\cup U_2)\cap U_3=(U_1\cap U_3)\cup (U_2\cap U_3)\]

이 주어진 조건을 만족한다는 것을 보여야 하는데, 이 때 $U_1\cap U_3$, $U_2\cap U_3$, 그리고 $U_1\cap U_2\cap U_3$는 모두 $\mathbb{R}^m$의 convex open subset으로서 주어진 조건을 만족하는 것을 안다. 비슷한 방식으로 각각의

\[U_1,\quad U_1\cup U_2, \quad U_1\cup U_2\cup U_3,\quad \cdots\]

이 모두 결론을 만족하는 것을 안다. 따라서 이로부터 nested open subset들의 sequence

\[U_1\subset U_1\cup U_2\subset U_1\cup U_2\cup U_3\cdots\]

에 앞선 (무한한) 귀납법을 적용하면 원하는 결과를 얻는다.

이제 마지막으로 $M$이 임의의 manifold일 경우, second countability를 이용하여 countable한 Euclidean chart로 $M$을 덮고 위와 마찬가지의 논증을 거치면 된다.

특히 증명에서, 만일 $M$이 그 자체로 compact였다면 dualilty map $D_M$은 정확하게 fundamental class $[M]$과의 cap product가 되었을 것이다.

뒤틀린 푸앵카레 쌍대성

$M$이 $A$-orientable이 아닐 경우 정리 11이 성립하지 않는 가장 큰 이유는, 근본적으로, $\or_M^A$가 constant sheaf가 되는 것에 실패하고 오직 locally constant이기만 하기 때문이다. 이는 covering space의 언어로 하자면, monodromy action이 stalk $A$에 nontrivial하게 작용하기 때문에, “한 바퀴”를 돌아왔을 때 stalk $A$가 꼬여서 붙게 되는 것으로 생각할 수 있다. 이 꼬임은 $A$의 automorphism이므로, 우리는 이를 보기 위해 $A$의 unit group $A^\times$의 bijection을 생각하면 충분했다.

이제 이 꼬임을 쌍대성에서 함께 고려하기 위해 우리는 homology with local coefficient을 정의한다.

정의 14 $M$ 위에 정의된 locally constant sheaf $\mathscr{L}$을 local coefficient system이라 부른다.

Local system $\mathscr{L}$의 stalk을 $L$이라 하자. 그럼 §피복공간, ⁋정리 11에 의하여, 우리는 임의의 path $\alpha:[0,1]\rightarrow M$이 주어질 때마다 stalk들 사이의 isomorphism $\mathscr{L}_{\alpha(0)}\rightarrow \mathscr{L}_{\alpha(1)}$이 존재하는 것을 안다. 이는 별다른 것이 아니라 covering space $\Spe(\mathscr{L})\rightarrow M$에서 path $\alpha$를 lift하여 얻어지는 isomorphism이다. 즉, 우리는 다음의 functor

\[\Pi_1(M)\rightarrow \Ab; \qquad x\mapsto \mathscr{L}_x\]

를 얻는다. 그럼 우리는 $\Delta^k$의 한 점 $e_0=(1,0,\ldots,0)$을 고정하여, $C_\bullet(M,\mathscr{L})$을 다음의 식

\[C_\bullet(M,\mathscr{L})=\bigoplus_{\sigma:\Delta^k\rightarrow M}\mathscr{L}_{\sigma(e_0)}\]

으로 정의한다. 어차피 각각의 $x$에 대하여 $\mathscr{L}_x\cong L$이지만, 이 정의의 핵심은 각각의 점에서의 $L$이 nontrivial한 automorphism을 통해 달라질 수 있다는 것이다. 그럼 이 chain complex의 differential map은, singular $k$-simplex $\sigma:\Delta^k \rightarrow M$과 계수 $a\in \mathscr{L}_{\sigma(e_0)}$에 대하여

\[\partial_k(a\sigma)=\sum_{i=0}^k(-1)^k\mathscr{L}_{\sigma_k}(a) (\sigma|_{[v_0,\ldots, \hat{v}_i,\ldots,v_k]})\]

로 정의된다. 여기서 $\mathscr{L}_{\sigma_k}$는 원래 simplex의 첫 번째 vertex $\sigma(e_0)$과, $k$번째 face의 첫 번째 vertex를 잇는 edge를 $M$으로 보내어 얻어진 path에 functor $\Pi_1(M) \rightarrow \Ab$를 적용하여 얻어진 것이다. 우리의 상황과 같이 좋은 경우, 우리는 $M$의 universal cover $\widetilde{M}$과 이 위에 작용하는 monodromy action (즉 Deck transformation), 그리고 monodromy representation $\pi_1(X)\rightarrow \Aut(A)$을 사용하여 다음의 chain complex

\[C(\widetilde{M})\otimes_{\mathbb{Z}[\pi_1(X)]} A\]

를 구성하여 얻어지는 chain complex를 생각하여도 이것이 위의 homology group과 같은 homology group을 주는 것을 안다.

이는 어떻게 보면 다소 과한 일반화라 할 수도 있는데, non-orientable 버전의 푸앵카레 쌍대성을 기술하기 위해 우리는 어차피 local coefficient system $\mathscr{L}$을 constant sheaf $\underline{A}$로 둘 것이기 때문이다. 그러나 이러한 일반화를 통해 우리는 코호몰로지 부분도 일반화가 가능하고, 이 일반화가 푸앵카레 쌍대성을 조금 더 투명하게 보여준다.

임의의 위상공간 $X$와 그 위에 정의된 sheaf $\mathscr{F}$에 대하여, global section functor

\[\Gamma(X,-):\Sh(X,\mathcal{A})\rightarrow \mathcal{A}\]

는 left exact functor이므로, 이 functor의 right derived functor가 존재한다. 이를 직접 계산하기 위해서는 Godement resolution을 사용하는데, 이는 다음과 같이 정의된다.

위상공간 $X$와 그 위에 정의된 sheaf $\mathscr{F}$를 생각하고, étalé space $\Spe(\mathscr{F})$를 생각하자. 우리는 $\mathscr{F}$가 정확하게 $\Spe(\mathscr{F})\rightarrow X$의 continuous section들의 sheaf임을 안다. 이제 임의의 열린집합 $U$에 대하여

\[\mathscr{G}_0(U)=\prod_{x\in U}\mathscr{F}_x\]

으로 정의하자. 즉 $\mathscr{G}_0$는 $\Spe(\mathscr{F})\rightarrow X$의 (연속일 필요가 없는) 집합론적인 section들의 sheaf이다. 우리의 아이디어는, 일반적으로 local하게 정의된 함수들이 이어붙였을 때 함수가 되지 않는 경우를 inclusion $\mathscr{F}\rightarrow \mathscr{G}_0$에 의해 유도되는 다음의 sequence

\[0 \rightarrow \mathscr{F}\rightarrow \mathscr{G}_0 \rightarrow \mathscr{Q}\rightarrow 0\]

을 통해 quotient sheaf $\mathscr{Q}$에 몰아넣어버리는 것이다. 그렇다면 sheaf $\mathscr{Q}$에 대해서도 마찬가지로

\[\mathscr{G}_1(U)=\prod_{x\in U}\mathscr{Q}_x\]

으로 정의되는 sheaf를 만들 수 있고, 이것이 다음의 Godement resolution

\[0 \rightarrow \mathscr{F}\rightarrow \mathscr{G}_0 \rightarrow \mathscr{G}_1\rightarrow \cdots\]

을 정의한다. 직관적으로 이는 $\Spe(\mathscr{F})$의 global section이 존재하지 못하도록 하는 부분을 $\mathscr{Q}$에, 그리고 다시 $\mathscr{Q}$의 global section이 존재하지 못하도록 하는 부븐을 $\mathscr{Q}’$에 담는 식으로 계속해서 반복하는 것이다. 이 resolution $\mathscr{G}_\bullet$은 injective resolution은 아니지만, 각각의 sheaf가 flabby (flasque) sheaf이기 때문에 이를 통해 global section functor의 right derived functor $R^i\Gamma$들을 계산할 수 있다.

정의 14 위상공간 $X$와 그 위에 정의된 sheaf $\mathscr{F}$에 대하여, Godement resolution의 global section들의 sequence

\[0 \rightarrow \mathscr{F}(X)\rightarrow \mathscr{G}_0(X)\rightarrow \mathscr{G}_1(X)\rightarrow \cdots\]

의 $k$번째 호몰로지를

\[H^k(X; \mathscr{F})\]

으로 적고, 이를 sheaf cohomology라 부른다.

이제 푸앵카레 쌍대성은 다음의 isomorphism

\[H^k(M;\mathscr{L})\cong H_{m-k}(M;\or_M^A\otimes \mathscr{L})\]

으로 일반화된다. 여기에서 원래의 푸앵카레 쌍대성으로 돌아가기 위해서는 우선 $\mathscr{L}$을 constant sheaf $\underline{A}$로 둔다. 그럼 manifold와 같이 좋은 경우에는 sheaf cohomology $H^k(M;\underline{A})$와 singular cohomology $H^k(M;A)$가 isomorphic하다는 것이 알려져 있으므로 다음의 isomorphism

\[H^k(M;A)\cong H_{m-k}(M;\or_M^A)\]

을 얻는다. 추가로 만일 $M$이 $A$-orientable일 경우 $\or_M^A$도 constant sheaf가 되므로, 이로부터 classical한 푸앵카레 쌍대성

\[H^k(M;A)\cong H_{m-k}(M;A)\]

을 복원할 수 있다.

푸앵카레 쌍대성과 cup product

지금까지 우리는 cohomology ring 위의 cup product와, 이로부터 정의된 cap product를 거리낌없이 사용해왔다. 그러나 누군가가 cup product가 무엇인지 묻는다면 대답하기가 곤란할 것이다. 이에 대한 답은 간단하다.

Cup product는 교집합의 Poincaré dual이다.

이것이 무슨 뜻인지를 엄밀하게 설명하기 위해서는 최소한 지금까지 들인 노력만큼이 추가로 필요하다. 그러나 이것이 직관적으로 무슨 뜻인지 살펴보는 것은 아마 다음 예시로 충분할 것이다.

예시 15 Torus $T^2=S^1\times S^1$을 생각하자. 그럼 우리는 Kunneth formula로부터 $T^2$의 cohomology가

\[H^0(T^2;\mathbb{Z})\cong \mathbb{Z}, \quad H^1(T^2;\mathbb{Z})\cong \mathbb{Z}^2,\quad H^2(T^2;\mathbb{Z})\]

임을 안다. 이 cohomology ring에서 non-trivial한 곱은 $H^1(T^2;\mathbb{Z})$의 두 generator $\alpha,\beta$들의 곱 뿐이다. 이들은, §코호몰로지, ⁋명제 3에 따르면, $T^2$의 두 원의 dual에 해당하는 것이다. 그럼 이들의 cup product를 취한 것은 $H^2(T^2;\mathbb{Z})$의 generator가 되며, 이는 cup product의 정의에서 바로 얻어지거나 대수적으로

\[H^2(T^2;\mathbb{Z})=H^1(T^2;\mathbb{Z})\otimes H^1(T^2;\mathbb{Z})\cong \mathbb{Z}\otimes \mathbb{Z}\cong \mathbb{Z}\]

가 $\alpha\otimes \beta$에 의해 생성되므로 당연하다.

이 때, 이들의 cup product가 $\alpha\times \beta$의 $\pm 1$이 아닌 상수배로 나타나지 않는 이유는 기하학적으로 다음과 같다. $\alpha$, $\beta$에 해당하는 homology class들을 $a,b$라 하면, $a$와 $b$의 교집합이 다음 그림과 같이 한 점에서만 만나기 때문이다.

이 때, 두 곡선이 어떻게 만나는지를 분류하여 하나는 양의 방향, 하나는 음의 방향으로 정하는 것이 곧 $T^2$의 orientation을 주는 것과 같다.

그렇다면 이 기하학적인 해석 하에서, $\alpha^2=0$인 것은 어떻게 설명할 수 있을까? 교집합 $a\cap a$를 문자 그대로 계산한다면 이는 다시 $a$가 된다. 이렇게 계산이 엉키는 이유는 두 cycle (이 경우에는 $a$의 두 copy)이 general position에 있지 않기 때문이다. 대략적으로, $\mathbb{R}^2$의 임의의 두 직선이 주어졌다 하면 이들은 (일치하는 경우를 포함해서) 서로 평행한 경우를 제외하면 일반적으로는 한 점에서 만날텐데, general position의 개념은 이를 일반화한 것이다.

이제 homology class가 $a$인 $T^2$의 곡선들을 생각하자. 그럼 이들은 서로 만나지 않을 가능성이 높고, 만약 만난다면 (마찬가지로 general position이 아닌, 접하는 경우를 제외하면) 다음의 모양

과 같이 만날 것이다. 이는 일견 두 개의 교점이 생기는 것 같지만, 위의 그림에서 양쪽 교점은 그 부호가 다르다, 즉, 가령 직선을 첫 번째 벡터, 곡선을 두 번째 벡터로 두고 외적을 할 경우, 하나는 바깥쪽, 다른 하나는 안쪽으로 들어가는 벡터가 나올 것이며 따라서 부호가 반대이다. 이렇게 두 교점이 상쇄되어 이들의 교집합은 $0$이 되고, 따라서 $\alpha\smile\alpha=0$이 된다.

---

참고문헌

[Hat] A. Hatcher, Algebraic Topology. Cambridge University Press, 2022.
[May] J. P. May, A concise course in algebraic topology.

---