호몰로지의 계산

우리는 이제 호몰로지를 실질적으로 계산할 수 있는 도구들을 살펴본다. 임의의 공간에 대해 이 공간의 호몰로지를 정의로부터 직접 계산하는 것은 거의 불가능한 일이므로, 우리는 큰 공간들을 작은 공간으로 쪼개고 이들의 호몰로지들로부터 큰 공간의 호몰로지를 계산하는 도구를 개발해야 한다. 가장 직관적인 상황은 Seifert-van Kampen 정리(§피복공간, ⁋정리 13)의 상황일 것이며, 이 경우 우리는 functor $\pi_1:\Top \rightarrow \Grp$이 colimit을 보존하는 것을 살펴보았다. 그런데 abelianization functor $\ab:\Grp \rightarrow \Ab$는 forgetful functor $U:\Ab \rightarrow \Grp$의 left adjoint functor이고 ([대수적 구조] §가환군, ⁋명제 7), left adjoint functor는 colimit을 보존하며 ([범주론] §수반함자, ⁋정리 9) first homology functor $H_1:\Top \rightarrow \Ab$는 이들의 합성이므로 (§피복공간, ⁋정리 15) 또한 colimit을 보존해야 한다. 특별히 §피복공간, ⁋따름정리 14와 같이 위상공간 $X$가 두 connected open subset $U,V$의 합집합으로 나타난다 하자. 그럼 category $\Ab$에서, 두 abelian group의 pushout은 이들의 direct sum의 coequalizer로 주어지므로 다음의 isomorphism

\[H_1(X)=H_1(U\cup V)\cong \frac{H_1(U)\oplus H_1(V)}{\left\langle (f(x),-g(x))\mid x\in H_1(U\cap V)\right\rangle}\tag{1}\]

이 성립해야 한다. 이번 글에서 우리는 이를 더 일반적인 방식으로 다루게 된다.

Relative homology

이를 위해서는 우선 호몰로지를 일반화할 필요가 있다. 공간 $X$와 임의의 부분공간 $A$에 대하여, $k$번째 relative chain group $C_k(X,A)$를 다음의 quotient

\[C_k(X,A):=C_k(X)/C_k(A)\]

으로 정의하자. 그럼 어렵지 않게 boundary map $\partial_k:C_k(X) \rightarrow C_{k-1}(X)$이 quotient group들 사이의 map $C_k(X,A) \rightarrow C_{k-1}(X,A)$를 유도하는 것을 안다. 이로부터 다음의 chain complex

\[\cdots \longrightarrow C_k(X,A)\overset{\partial}{\longrightarrow} C_{k-1}(X,A)\longrightarrow\cdots\]

를 만들 수 있다.

정의 1 위의 chain complex의 $k$번째 호몰로지 $H_k(X,A)$를 relative homology라 부른다.

이제 category $\Ch_{\geq 0}(\Ab)$에서의 short exact sequence

\[0 \rightarrow C_\bullet(A) \rightarrow C_\bullet(X) \rightarrow C_\bullet(X,A) \rightarrow 0\]

을 생각하자. 그럼 [호몰로지 대수학] §긴 완전열, ⁋정리 1에 의하여 다음의 long exact sequence

\[\cdots \rightarrow H_k(A) \rightarrow H_k(X) \rightarrow H_k(X,A)\rightarrow H_{k-1}(A) \rightarrow \cdots\]

이 존재한다. 이 때 connecting map $H_k(X,A) \rightarrow H_{k-1}(A)$는 $H_k(X,A)$의 임의의 cycle(의 임의의 representative)에 boundary map을 취한 것에 불과하다. 뿐만 아니라, 만일 continuous map $f:X \rightarrow Y$가 $f(A)\subseteq B$를 만족한다면 $f$가 기존의 chain map $C_\bullet(X)\rightarrow C_\bullet(Y)$ 외에도 $C_\bullet(A) \rightarrow C_\bullet(B)$를 유도하고, 다음 diagram

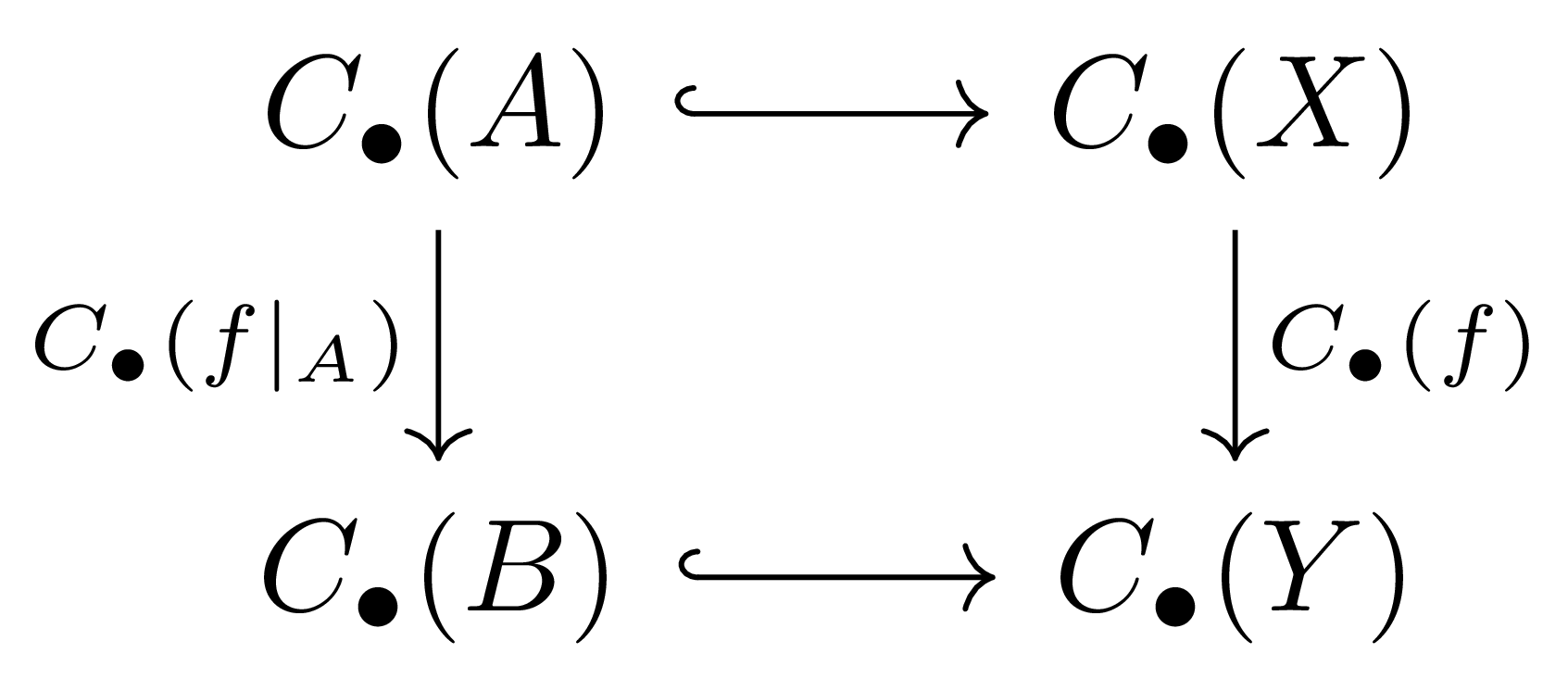
이 commute한다는 것으로부터 chain map $C_\bullet(X,A) \rightarrow C_\bullet(Y,B)$ 또한 유도된다. 즉, 이러한 조건을 만족하는 $f:(X,A) \rightarrow (Y,B)$는 homology에서의 map $H_k(f):H_k(X,A) \rightarrow H_k(Y,B)$ 또한 유도한다. 그럼 §호모토피, ⁋명제 6을 $X$와 $A$ 각각에 적용하고 [호몰로지 대수학] §Digram chasing, ⁋따름정리 2를 사용하면 이 조건을 만족하는 homotopic한 연속함수들 $f,g$가 호몰로지에서 같은 함수를 유도하는 것을 안다.

Excision theorem

직관적으로 $(X,A)$에 대한 realtive homology $H_\bullet(X,A)$는 inclusion $C_\bullet(A)\hookrightarrow C_\bullet(X)$의 cokernel에 해당하는 chain complex $C_\bullet(X,A)$의 호몰로지이다. 직관적으로 이 과정에서 $C_\bullet(A)$에 대한 정보는 quotient를 취하며 사라지게 되므로, $A$ 안에 들어있는 부분집합을 전체에서 뺀다고 해서 relative homology가 변하지 않을 것이라는 것은 직관적으로는 그럴듯해보인다. 이는 다음의 약한 조건 하에서는 참이다.

정리 2 (Excision theorem) 공간 $X$의 부분공간 $A$와, $A$의 부분공간 $Z$가 $\cl Z\subseteq \interior A$를 만족한다고 하자. 그럼 inclusion

\[(X\setminus Z, A\setminus Z)\hookrightarrow (X,A)\]

에 의해 유도되는

\[H_k(X\setminus Z, A\setminus Z)\rightarrow H_k(X,A)\]

는 isomorphism이다.

그러나 이 정리가 직관적으로 자명한 것에 비해, 그 증명은 다소 기술적인 부분이 있어 여기에서는 그 증명을 생략하기로 한다.

한편 우리는 기하적인 상황에서 이와 같이 $A$에 들어있는 정보를 무시하는 방법을 알고 있다. 즉, $A$를 하나의 점으로 줄이는 quotient space $X/A$이다. 그럼 homology $H_k(X/A)$와 relative homology $H_k(X,A)$ 사이의 관계가 있다는 것이 합리적인 추측이다. 물론 위의 정리와 마찬가지로 이는 $A$가 아주 이상한 공간은 아니어야 가능하다.

정의 3 공간 $X$와 부분공간 $A$에 대하여, 이들 $(X,A)$가 good pair라는 것은 $A$가 닫힌집합이고, $X$의 적당한 열린집합 $U$가 존재하여 $A\subset U$이고 $A$가 $U$의 strong deformation retract인 것이다.

Good pair $(X,A)$가 주어졌다 하고, $U$가 정의 3의 가정을 만족하는 열린집합이라 하자. 그럼 다음의 diagram

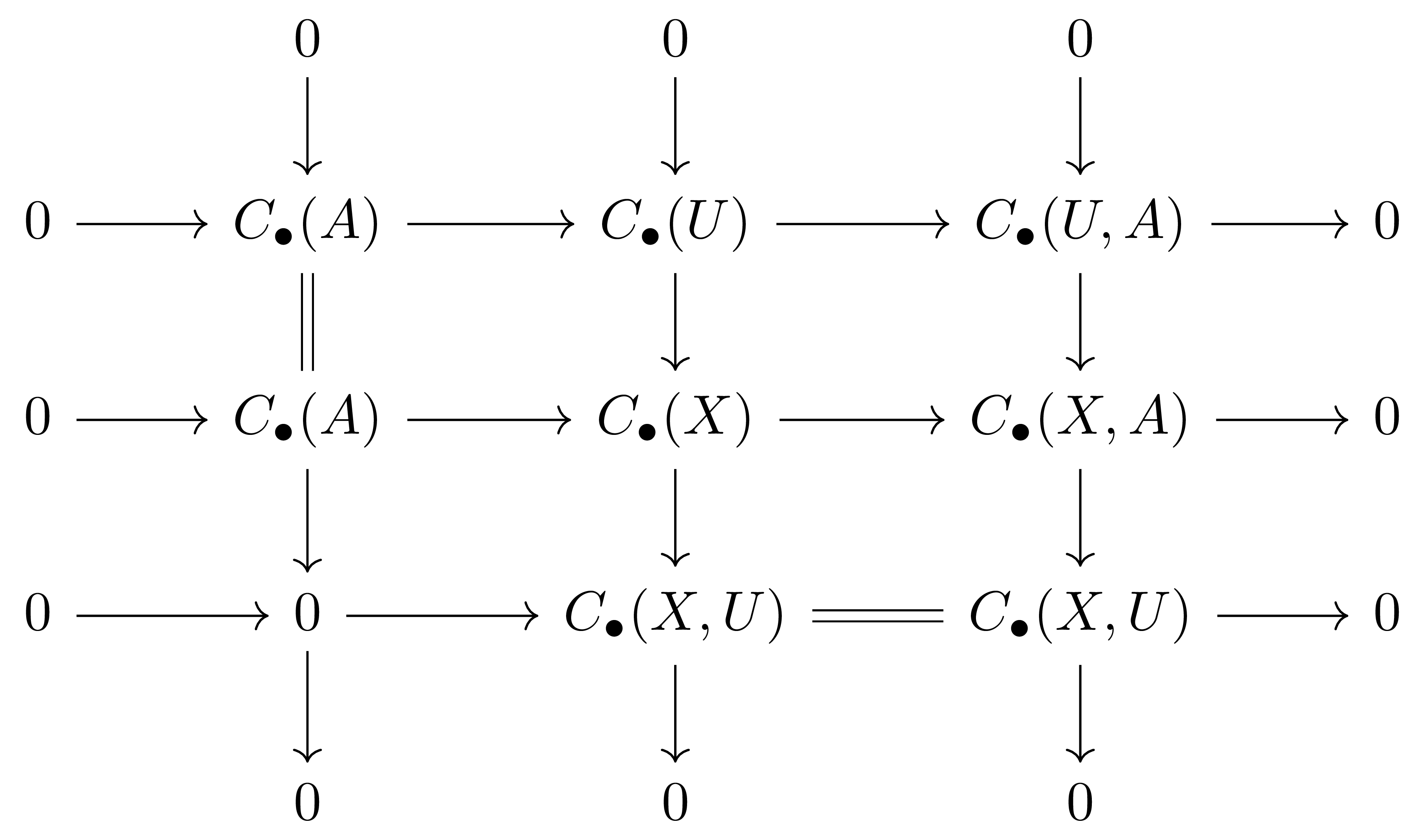
에서, 각 행은 모두 exact이며 처음 두 열도 exact이므로 [호몰로지 대수학] §Diagram chasing, ⁋따름정리 7에 의하여 chain complex들의 short exact sequence

\[0\rightarrow C_\bullet(U,A)\rightarrow C_\bullet(X,A)\rightarrow C_\bullet(X,U)\rightarrow 0\]

그리고 이로부터 얻어지는 long exact sequence

\[\cdots \rightarrow H_k(U,A) \rightarrow H_k(X,A)\rightarrow H_k(X,U)\rightarrow H_{k-1}(U,A)\rightarrow \cdots\]

를 얻는다. 그런데 $A$가 $U$의 strong deformation retract라는 가정으로부터 $H_k(U,A)=0$이 모든 $k$에 대해 성립하고 따라서 isomorphism $H_k(X,A)\cong H_k(X,U)$이 모든 $k$에 대해 성립한다.

한편 임의의 closed subspace $A$에 대하여, $A$를 한 점으로 줄여서 만드는 quotient space $X/A$가 잘 정의되며, 이 때 projection $X \rightarrow X/A$는 $A$를 한 점 $[A]$으로 보내고, $A$ 바깥에서는 homeomorphism인 함수이다. 이 때, 포함관계

\[\{[A]\}\subseteq U/A\subseteq X/A\]

에 위와 마찬가지 논증을 적용하면 $U/A$가 한 점 $[A]$로 strong deformation retract하므로 $H_k(U/A,[A])=0$으로부터 다음의 isomorphism

\[H_k(X/A, [A])\cong H_k(X/A, U/A)\]

을 얻으며 이들은 quotient map에 의해 유도되는 다음의 diagram

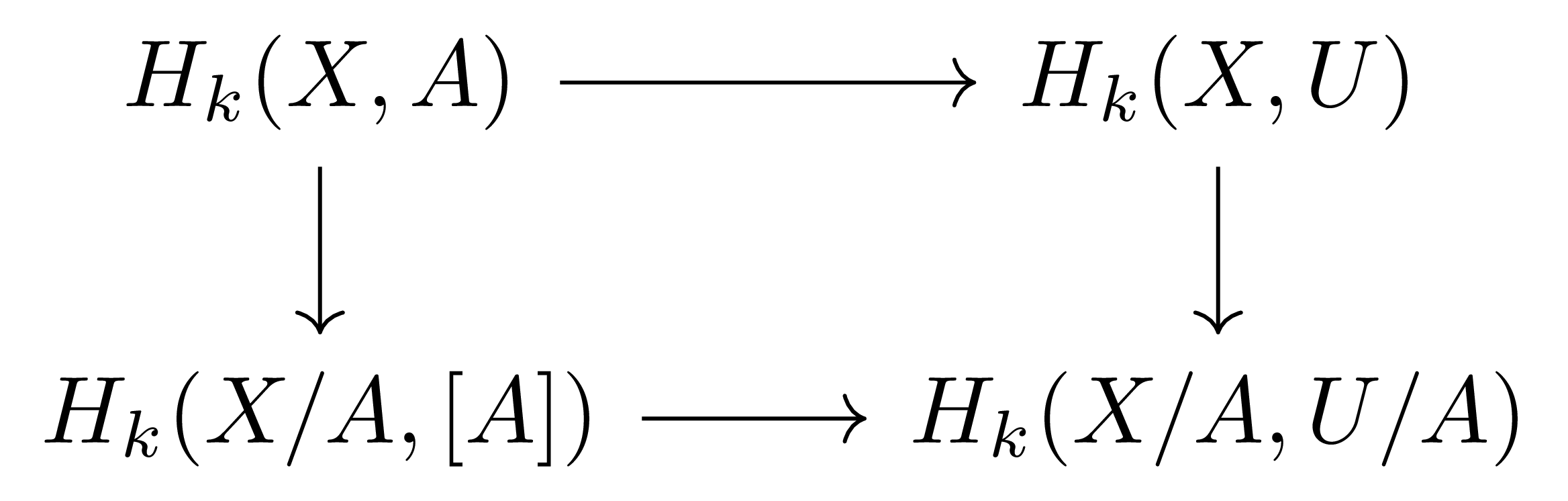
에 넣을 수 있다. 이제 $(X,A)$가 good pair라는 가정으로부터, $A\subset U\subset X$는 정리 2의 조건 $\cl A\subseteq \interior U$를 만족하고 따라서 inclusion

\[(X\setminus A, U\setminus A)\hookrightarrow (X,U)\]

에 의해 유도되는 $H_k(X\setminus A, U\setminus A)\rightarrow H_k(X,U)$는 isomorphism이며, 마찬가지로 포함관계 $\{[A]\}\subseteq U/A\subseteq X/A$에 정리 2을 적용하면 다음의 map

\[H_k((X/A)\setminus [A], (U/A)\setminus [A])\]

이 isomorphism이라는 것을 안다. 이들은 마찬가지로 quotient map에 의해 유도되는 다음의 diagram

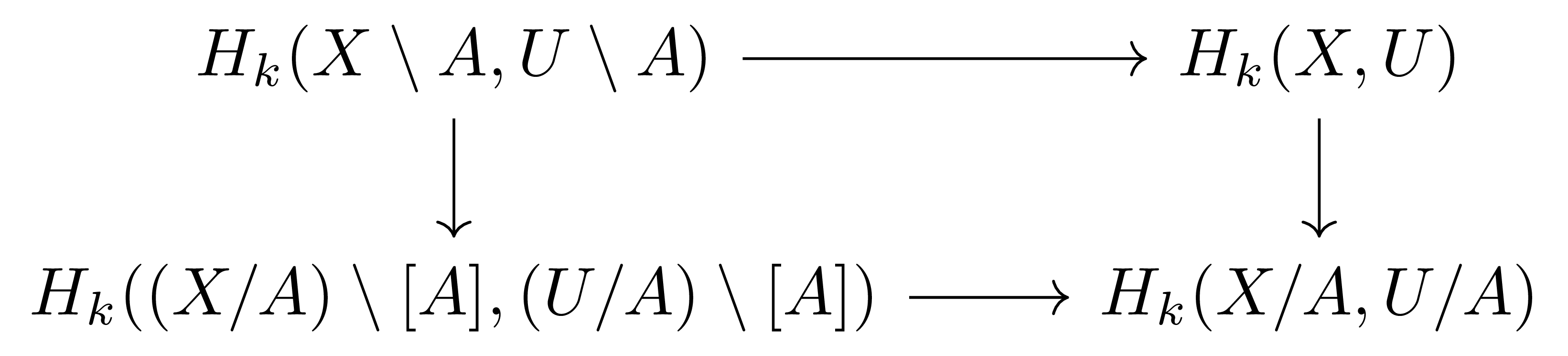
에 들어가는데, 이 때 왼쪽 수직방향의 $H_k(X\setminus A, U\setminus A)\rightarrow H_k((X/A)\setminus [A], (U/A)\setminus [A])$는 quotient map $p:X\rightarrow X/A$가 $A$ 바깥에서는 homeomorphism이라는 가정으로부터 isomorphism이 된다. 이 결과들을 종합하면 다음의 isomorphism

\[H_k(X,A)\cong H_k(X/A,[A])\tag{2}\]

을 얻는다.

한편, §호몰로지, ⁋명제 11와 [호몰로지 대수학] §Digram chasing, ⁋따름정리 2에 의해, 임의의 공간 $X$와 한 점 $x\in X$에 대하여 다음의 long exact sequence

\[\begin{aligned}\cdots &\rightarrow H_k(x)\rightarrow H_k(X)\rightarrow H_k(X,x) \rightarrow H_{k-1}(x)\rightarrow\cdots \\\cdots&\rightarrow H_1(x)\rightarrow H_1(X) \rightarrow H_1(X,x) \rightarrow H_0(x) \rightarrow H_0(X)\rightarrow H_0(X,x)\rightarrow 0\end{aligned}\]

는 모든 $k>1$에 대하여 isomorphism $H_k(X)\cong H_k(X,x)$을 준다. 뿐만 아니라, $k=1$인 경우의 long exact sequence를 보면

\[0 \rightarrow H_1(X) \rightarrow H_1(X, x) \overset{\partial}{\longrightarrow} H_{0}(x) \overset{\iota_\ast}{\longrightarrow} H_{0}(X)\]

인데, 이 때 $\iota_\ast$는 $H_0(x)$의 generator를 $x$를 포함하는 $X$의 path component로 보내므로 injective이고, 따라서 $\partial$은 zero map이며 이로부터 마찬가지의 isomorphism $H_1(X)\cong H_1(X,x)$을 얻는다.

한편 $\iota_\ast$가 injective라는 사실로부터 우리는 다음의 long exact sequence

\[0 \rightarrow H_0(x)\rightarrow H_0(X) \rightarrow H_0(X,x)\rightarrow 0\]

를 얻고, 이로부터 isomorphism $H_0(X,x)\cong H_0(X)/\mathbb{Z}$를 얻는다. 기하학적으로 이는 $H_0(X)$의 path component 중 $x$를 포함하는 path component를 없애는 것과 같다. 표기의 깔끔함을 위해 reduced homology $\widetilde{H}_k(X)$를 고정된 $x\in X$에 대하여

\[\widetilde{H}_k(X)=H_k(X,x)\]

으로 정의하면, 위의 isomorphism (2)의 우변을 $\widetilde{H}_k(X/A)$로 바꾸어 다음과 같이 쓸 수 있다.

명제 4 Good pair $(X,A)$에 대하여, quotient map $X \rightarrow X/A$는 모든 $k$에 대해 다음의 isomorphism

\[H_k(X,A)\cong \widetilde{H}_k(X/A)\]

을 유도한다.

심플렉스 호몰로지와 특이 호몰로지

한편 relative homology는 정의한 방식은 $\Ch_{\geq 0}(\Ab)$에서의 monomorphism $C_\bullet(A)\rightarrow C_\bullet(X)$에 cokernel을 취한 것이었으므로, 이 과정은 $C^\Delta_\bullet(A) \rightarrow C^\Delta_\bullet(X)$에 대해 반복해도 된다. 그럼 그 결과로 우리는 simplicial homology 버전의 realtive homology $H_n^\Delta(X,A)$를 얻게 된다. 이제 simplicial homology는 “singular하지 않은” chain들이므로, inclusion

\[C_\bullet^\Delta(X) \rightarrow C_\bullet(X)\]

에 의해 유도되는 canonical homomorphism

\[H_\bullet^\Delta(X)\rightarrow H_\bullet(X)\tag{3}\]

이 존재하며, 비슷하게 다음의 canonical homomorphism들

\[H_\bullet^\Delta(A)\rightarrow H_\bullet^\Delta(A),\qquad H_\bullet^\Delta(X,A)\rightarrow H_\bullet(X,A)\]

이 존재한다. 그럼 이들은 [호몰로지 대수학] §긴 완전열, ⁋명제 2에 의하여 다음의 commutative diagram

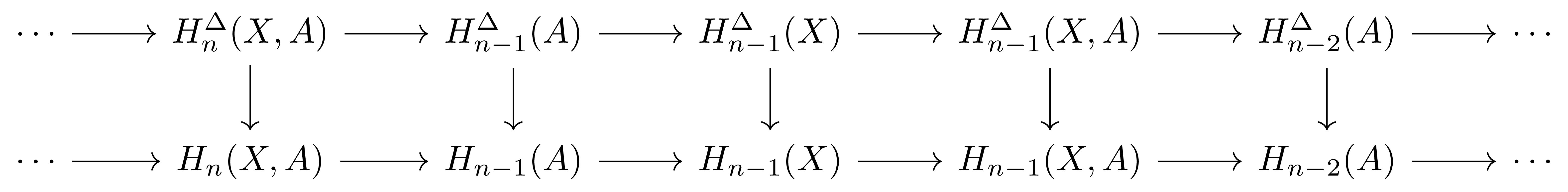
을 정의한다. 이를 사용하면 다음이 성립한다.

정리 5 임의의 $\Delta$-complex $X$에 대하여, (3)의 homomorphism은 isomorphism이다.

증명

대략적인 흐름을 소개한다. 위의 commutative diagram에 의하여, $X$의 $\Delta$-complex 구조가 정의하는 filtration

\[X_0\subset X_1\subset\cdots\subset X_l=X\]

을 생각한 후 [호몰로지 대수학] §Diagram chasing, ⁋따름정리 2를 다음 diagram

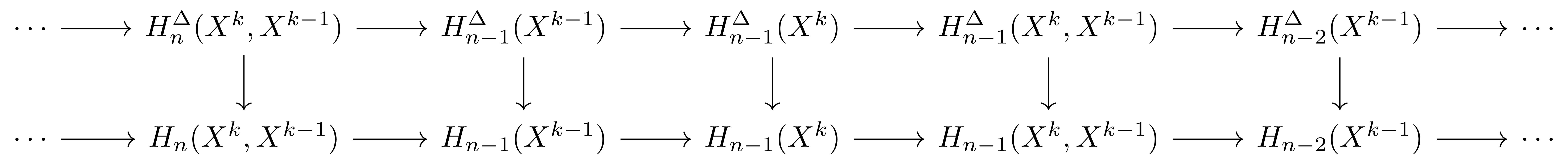
에 적용하여 귀납법을 돌리자. 귀납법을 위해서는 임의의 $n$과 임의의 $k$에 대하여 relative homology들 사이의 homomorphism

\[H_n^\Delta(X^k, X^{k-1})\rightarrow H_n(X^k, X^{k-1})\]

이 isomorphism임만 보이면 충분하다. 이를 가정하고 나면 우선 §호몰로지, ⁋명제 10에 의해 $k=1$일 때 $H_n^\Delta(X^0)\cong H_n(X^0)$가 모든 $n$에 대해 성립하므로 [호몰로지 대수학] §Diagram chasing, ⁋따름정리 2에 의해 $H_n^\Delta(X^1)\cong H_n(X^1)$임을 보일 수 있고, 다시 이로부터 귀납적으로 큰 $k$에 대해 원하는 isomorphism을 만들 수 있기 때문이다.

우선 정의에 의하여, $C_\bullet^\Delta(X^k, X^{k-1})$은 오직 $n=k$일 때만 nontrivial하며, 따라서 $H_n^\Delta(X^k, X^{k-1})$은 오직 $n=k$일 때만 ($k$-simplex들로 생성되는) nontrivial free abelian group이고, 다른 경우는 모두 trivial하다.

Singular homology에 대해서도 비슷한 결과가 성립하는데, 구체적으로 $H_n(\Delta^k,\partial\Delta^k)$는 $n=k$일 때만 free abelian group이며 그 generator는 $\id:\Delta^k \rightarrow \Delta^k$이다. 이를 확인하려면 $\Lambda$를 $\Delta^k$의 모든 $k-1$차원 face 중 하나만 뺀 것으로 정의하고, $(\Delta^k, \partial\Delta^k, \Lambda)$에 해당하는 long exact sequence

\[\cdots\rightarrow H_n(\Delta^k,\Lambda)\rightarrow H_n(\Delta^k, \partial\Delta^k)\rightarrow H_{n-1}(\partial\Delta^k, \Lambda)\rightarrow H_{n-1}(\Delta^k,\Lambda)\rightarrow \cdots\]

를 보면 $H_\bullet(\Delta^k,\Lambda)$들은 $\Delta^k$가 $\Lambda$로 deformation retract하므로 $0$이고 따라서 $H_k(\Delta^k, \partial\Delta^k)\cong H_{n-1}{\partial\Delta^k,\Lambda}$이며, 한편 good pair $(\partial\Delta^k,\Lambda)$에 대하여 quotient space $\partial\Delta^k/\Lambda$가 quotient space $\Delta^{k-1}/\partial\Delta^{k-1}$와 homeomorphic하므로 이들을 이용하면

\[H_k(\Delta^k, \partial\Delta^{k})\cong H_{k-1}(\Delta^{k-1}, \partial\Delta^{k-1})\]

을 얻고, 따라서 귀납적으로 원하는 결과를 보일 수 있다.

이 과정을 살펴보면, $H_k(\Delta^k,\partial\Delta^k)$의 (singular homology로서의) generator는 정확히 $k$-simplex $\Delta^k$와 같다는 것을 안다. Pair $(X^k,X^{k-1})$은, 이러한 pair들 $(\Delta^k,\partial\Delta^k)$들의 합집합이므로, §호몰로지, ⁋명제 9에 의해 원하는 결과를 얻는다.

메이어-피토리스 열

분량상 증명을 적지는 않았지만, 정리 2의 excision theorem은 호몰로지 이론을 다룰 때 요긴하게 쓰인다. 가령 정리 5의 증명에서 우리는 $k-1$ 미만의 simplex들을 무시할 때 excision theorem을 사용하였고, 이를 통해 귀납법을 사용할 수 있었으며 그 때의 base step은 one-point space의 homology였다. 이 과정이 본질적으로 homology가 만족해야 할 모든 성질들을 가지고 있는 것으로 볼 수 있으며, 이를 공리화하면 다음과 같다.

정의 6 (Eilenberg-Steenrod axioms) 위상공간들의 pair들의 category에서 abelian group들의 category로의 functor들 $H_k$과, 이들 사이의 natural transformation

\[\partial:H_k(X,A)\rightarrow H_{k-1}(A,\emptyset):=H_{k-1}(A)\]

들에 대하여, Eilenberg-Steenrod axiom은 다음의 공리들을 뜻한다.

• (Homotopy) 두 homotopic map $(X,A) \rightarrow (Y,B)$이 주어졌다면, 이들이 유도하는 두 homomorphism들 $H_k(X,A) \rightarrow H_k(Y,B)$들도 동일하다.
• (Excision) 정리 2의 조건을 만족하는 $(X,A,Z)$에 대하여, $(X\setminus Z, A\setminus Z)\hookrightarrow (X,A)$는 isomorphism을 유도한다.
• (Dimension) One-point space $\ast$에 대하여, $H_k(\ast)=0$이 모든 $k>0$에 대해 성립한다.
• (Additivity) 만일 $X=\coprod X_\alpha$라면, $H_k(X)\cong\bigoplus H_k(X_\alpha)$이다.

• (Exactness) 각각의 pair $(X,A)$와, 두 inclusion $(A,\emptyset) \hookrightarrow (X,\emptyset)$ 그리고 $(X,\emptyset)\hookrightarrow (X,A)$들은 다음의 long exact sequence

  \[\cdots \rightarrow H_k(A)\rightarrow H_k(X) \rightarrow H_k(X,A) \rightarrow H_{k-1}(A)\rightarrow \cdots\]

  에 들어간다.

그럼 Eilenberg와 Steenrod의 결과는 이러한 방식으로 정의된 homology theory들은, 만일 coefficient group $H_0(\ast)$가 고정된다면 이들은 모두 naturally isomorphic하다는 것을 보여준다. 예를 들어 우리는 앞서 simplicial homology와 singular homology가 $\Delta$-complex 위에서는 일치한다는 것을 증명하였으며, 그 증명을 하나하나 분리해보면 본질적으로 우리가 사용한 것은 위의 정의 6의 공리들임을 확인할 수 있다. 호몰로지의 실용적인 계산을 위해서는 CW complex 위에 정의된 cellular homology를 도입하는 것이 좋은데, 마찬가지로 이 homology 또한 위의 공리들을 만족하고 따라서 이 또한 simplicial homology, singular homology와 같은 계산을 준다.

한편 이들 homology theory들은 모두 coefficient group이 $\mathbb{Z}$로 고정되어 있는 상태인데, 이를 임의의 abelian group $A$로 바꾸어도 정의 6의 모든 공리는 변함없이 성립한다. 실제로 singular homology 혹은 simplicial homology를 정의할 때, chain group들

\[C^\Delta_\bullet(X),\qquad C_\bullet(X)\]

을 free abelian group이 아니라, free $A$-module들

\[C^\Delta_\bullet(X;A):=C^\Delta_\bullet(X)\otimes_\mathbb{Z}A,\qquad C_\bullet(X;A):=C_\bullet(X)\otimes_\mathbb{Z}A\]

로 잡았더라면 이러한 종류의 호몰로지를 얻었을 것이다.

호몰로지의 대부분의 성질들은 정의 6의 공리들로부터 나온다. 예를 들어, 이 글의 목표인 식 (1)의 일반화를 이로브터 유도할 수 있다. 위상공간 $X$가 두 열린집합들의 합집합 $X=U\cup V$로 나타난다 하자. 그럼 다음의 inclusion

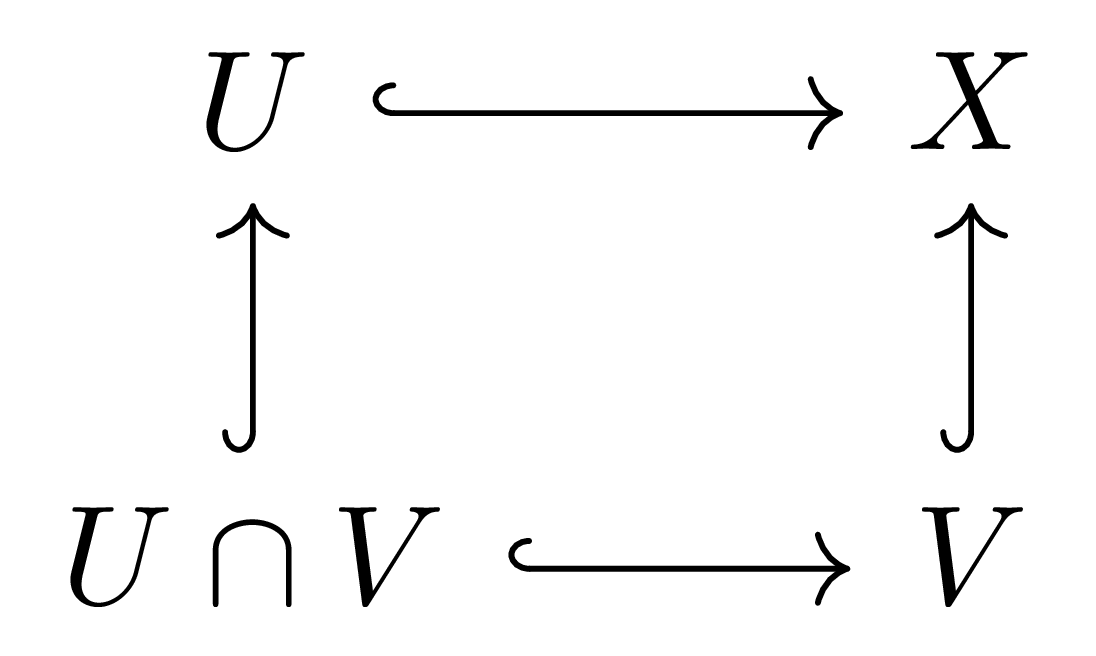
들에 homology를 취하면 exactness에 의하여 long exact sequence들 사이의 morphism을 얻으며, 이 때 inclusion

\[(V,U\cap V)\rightarrow (X,U)\]

은 excision axiom에 의하여 homology 상에서 isomorphism을 유도하므로, 위의 morphism 중 여기에 해당하는 것들은 모두 isomorphism이다. 즉 다음의 long exact sequence morphism

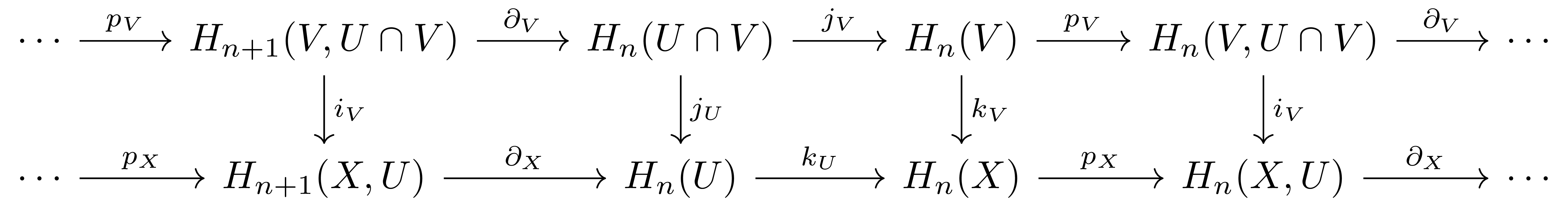
을 얻는다. 여기서 $i,j,k$들은 각각의 inclusion에 의해 유도되는 함수들이고, $\partial$들은 connecting map이며 $p$들은 cokernel morphism들이다. 편의를 위해 index들은 생략하였다. 이제 이 long exact sequence morphism을 $\alpha$라 하고, $\alpha$의 mapping cone exact sequence

\[\begin{aligned}\cdots &\overset{\overline{\partial}}{\longrightarrow} H_{n+1}(X)\oplus H_{n+1}(V, U\cap V)\overset{\overline{\Phi}}{\longrightarrow} H_{n+1}(X,U)\oplus H_n(U\cap V)\overset{\overline{\Psi}}{\longrightarrow} H_n(U)\oplus H_n(V)\\ \phantom{\cdots}&\overset{\overline{\partial}}{\longrightarrow} H_n(X)\oplus H_n(V, U\cap V)\rightarrow \cdots\end{aligned}\]

를 $\Cone(\alpha)$라 하자. 그럼 앞선 excision axiom의 결과에 의하여, 다음의 long exact sequence

\[\cdots \rightarrow 0 \rightarrow H_{n+1}(V, U\cap V)\rightarrow H_{n+1}(X,U)\rightarrow 0 \rightarrow \cdots\tag{4}\]

가 존재하며, 이를 사용하면 $\Cone(\alpha)$를 이 자명한 long exact sequence와 다음의 long exact sequence

\[\cdots \rightarrow H_{n+1}(U)\oplus H_{n+1}(V)\rightarrow H_{n+1}(X)\rightarrow H_n(U\cap V)\rightarrow H_n(U)\oplus H_n(V)\rightarrow\cdots\tag{5}\]

의 direct sum으로 나타낼 수 있다는 것을 안다. 이 때 $\Cone(\alpha)$와 (4)가 모두 exact이므로 (5) 또한 exact이며, (5)의 exact sequence의 differential map들은 mapping cone exact sequence에서 isomorphism들 $i_V$가 정의하는 change of basis를 통해 얻어진다. 이를 명시적으로 계산하면 다음을 얻는다.

명제 7 (Mayer-Vietoris sequence) 위상공간 $X$가 두 열린집합들의 합집합 $X=U\cap V$로 나타난다 하고, 이 위에 정의된 homology theory $H$를 생각하자. 그럼 long exact sequence

\[\cdots \rightarrow H_{n+1}(U)\oplus H_{n+1}(V)\overset{\Psi}{\longrightarrow} H_{n+1}(X)\overset{\partial}{\longrightarrow} H_n(U\cap V)\overset{\Phi}{\longrightarrow} H_n(U)\oplus H_n(V)\rightarrow\cdots\]

가 존재하며, 이 때 함수들 $\Psi, \Phi$은 각각

\[\Psi(u,v)=u+v,\qquad \Phi(x)=(x,-x)\]

으로 주어진다.

특히 $n=1$인 경우를 보면 우리는 맨 처음에 Seifert-van Kampen 정리를 abelianization을 통해 옮겨온 (1)을 얻으며, 이러한 측면에서 Mayer-Vietoris sequence는 Seifert-van Kampen 정리의 homology 버전으로 생각할 수 있다.

---

참고문헌

[Hat] A. Hatcher, Algebraic Topology. Cambridge University Press, 2022.
[May] J. P. May, A concise course in algebraic topology.

---