합곱

앞서 cohomology를 도입하며 우리는 cohomology의 가장 큰 장점 중 하나가 이 위에 자연스럽게 정의된 곱셈구조라 하였다. 그렇다면 이 구조가 왜 호몰로지에서는 보이지 않았는지 또한 합리적인 의문일 것인데, 이번 글에서 이 곱셈구조를 정의하면, 본질적으로 cohomology가 contravariant functor이기 때문이라는 것이 드러난다.

코호몰로지의 외적

Commutative ring \(A\)를 고정하고, \(A\)-module들의 chain complex \(C_\bullet,D_\bullet\)이 주어졌다 하자. 이들의 dual sequence

\[(C^\vee)^\bullet=\Hom_A(C_\bullet,A),\qquad (D^\vee)^\bullet=\Hom_A(D_\bullet,A)\]

그리고

\[((C\otimes D)^\vee)^\bullet=\Hom_A((C\otimes D)_\bullet,A)\]

에 대하여, 우리는 우선

\[\times:(C^\vee\otimes D^\vee)^\bullet\rightarrow ((C\otimes D)^\vee)^\bullet\]

을 정의한다. 이를 위해서는 좌변의 simple tensor \(\phi\otimes \psi\)를 받아 \((C\otimes D)_\bullet\)에서 \(A\)의 함수를 하나 대응시켜주면 되고, 이는 다시 \((C\otimes D)_\bullet\)의 simple tensor에서의 값으로 정의된다. 만일 \(\phi\in (C^\vee)^p,\psi\in (D^\vee)^q\)라면, 우리는 정확히 \(C_p\otimes D_q\)에 속하는 simple tensor \(\alpha\otimes \beta\)에 대해서만

\[(\phi\times\psi):(C\otimes D)_\bullet \rightarrow A;\qquad (\alpha\otimes \beta)\mapsto (-1)^{\deg(\alpha)\deg(\beta)}\phi(\alpha)\psi(\beta)\]

이고, 나머지에 대해서는 \(0\)인 함수로 이 대응을 정의한다. 그럼 어렵지 않게 이것이 cochain complex들 사이의 morphism인 것을 확인할 수 있으며 따라서 \(\times\)는 cohomology의 함수

\[\bar{\times}: H^\bullet(C^\vee\otimes D^\vee)\rightarrow (H(C^\vee)\otimes H(D^\vee))^\bullet\rightarrow H^\bullet((C\otimes D)^\vee)\]

를 정의한다.

이제 두 위상공간 \(X,Y\)의 \(A\)-valued chain

\[C_\bullet(X;A),\qquad C_\bullet(Y;A)\]

들이 주어졌다 하자. \(C_\bullet=C_\bullet(X;A), D_\bullet=C_\bullet(Y;A)\)로 두고 위의 cochain map을 취하면 우리는 이를 §코호몰로지의 Alexander-Whitney map \(\AW\)가 유도하는 함수와 합성하여 다음의 cochain map

\[(C^\vee(X;A)\otimes C^\vee(Y;A))^\bullet \overset{\times}{\longrightarrow} \Hom_A(C_\bullet(X;A)\otimes C_\bullet(Y;A),A)\overset{\Hom(\AW,A)}{\longrightarrow} \Hom_A(C_\bullet(X\times Y;A),A)=(C^\vee)^\bullet(X\times Y)\]

을 얻고, 다시 이를 cohomology 레벨로 내리면 각각의 \((p,q)\)마다 다음의 \(A\)-module homomorphism

\[{\AW^\ast}\circ{(-\mathbin{\bar{\times}}-)}:H^p(X;A)\otimes_A H^q(Y;A)\rightarrow H^{p+q}(X\times Y;A)\]

을 얻는다. 혼동의 여지가 없을 때에는 이를 간단히 \(\times\)로 적기로 하자.

합곱의 정의와 기본 성질들

이제 우리는 합곱을 정의할 수 있다.

정의 1 Commutative ring \(A\)와 위상공간 \(X\)에 대하여, 다음의 합성

\[{\smile}:H^\bullet(X;A)\otimes_A H^\bullet(X;A)\overset{\AW^\ast\circ\bar{\times}}{\longrightarrow}H^\bullet(X\times X)\overset{\Delta^\ast}{\longrightarrow} H^\bullet(X)\]

을 \(H^\bullet(X;A)\) 위의 cup product_합곱이라 부른다.

이 단계에서 cup product가 왜 homology에서는 명시적으로 보이지 않았는지가 나타난다. Eilenberg-Zilber map을 사용하면

\[H_p(X;A)\otimes_A H_q(X;A)\rightarrow H_{p+q}(X\times X;A)\]

까지는 만들 수 있을 것이나, diagonal map \(\Delta:X\rightarrow X\times X\)에 homology functor를 취하는 것은 covariant이므로 방향이 맞지 않을 것이기 때문이다.

명시적으로, 임의의 \(\alpha\in H^p(X;A)\), \(\beta\in H^q(X;A)\)에 대하여, \(\alpha\smile\beta\in H^{p+q}(X;A)\)는 임의의 chain \(\sigma:\Delta^{p+q}\rightarrow X\) 위에서 다음의 식

\[(\alpha\smile\beta)(\sigma)=(\Delta^\ast\AW^\ast(\alpha\mathbin{\bar{\times}}\beta))(\sigma)=(\alpha\mathbin{\bar{\times}}\beta)(\AW(\Delta(\sigma)))=(-1)^{pq}\alpha(\text{front face of $\sigma$})\beta(\text{back face of $\sigma$})\]

으로 주어진다. 이 명시적인 계산에서 알 수 있듯, de Rham cohomology에서 cup product는 아주 익숙한 것으로, differential form들의 wedge product에 해당하는 것이다.

그럼 그 이름에서 짐작할 수 있듯, cup product는 cohomology ring 위의 곱셈구조를 정의한다. 그런데 \(H^\bullet(X;A)\)는 graded ring이기도 하므로, 이 위에 정의된 곱셈의 commutativity를 논할 때는 다음과 같이 주의를 기울여야 한다.

명제 2 위상공간 \(X\)와 commutative ring \(A\)를 고정하자. 그럼

\[(H^\bullet(X;A), {\smile}, 1)\]

은 grade-commutative, \(\mathbb{N}\)-graded \(A\)-algebra를 이룬다. 여기서 \(1\in H^0(X;A)\)는 \(X\)의 임의의 \(\Delta\)-simplex를 모두 \(1\in A\)로 보내는 cocycle이다.

즉, homogeneous cycle들 \(\alpha\in H^p(X;A),\beta\in H^q(X;A),\gamma\in H^r(X;A)\)에 대하여,

• (Unit) \(1\smile\alpha=\alpha\smile 1=\alpha\)
• (Associativity) \((\alpha\smile\beta)\smile\gamma=\alpha\smile(\beta\smile\gamma)\)
• (Grade-commutativity) \(\alpha\smile\beta=(-1)^{pq}\beta\smile\alpha\)

이 성립한다. 이를 보이기 위해서는, 당연히, \(\Top^2\) (혹은 \(\Top^3\))에서 \(\Ch_{\geq 0}(\lMod{A})\)로의 functor들에 §Acyclic models theorem, ⁋정리 3를 적용하면 된다.

합곱의 함자적 성질들

위에서 증명한 성질은 functor \(H^\bullet(-;A)\)의 대상들이, 처음 정의할 때는 \(\lMod{A}\)로의 functor로 정의하였지만, 최종적으로는 \(\gr_{\mathbb{N}}\Alg{A}\)에 도착한다는 것을 보여준다. 그렇다면 \(H^\bullet(-;A)\)가 \(\Top\)에서 \(\gr_\mathbb{N}\Alg{A}\)로의 functor인지를 궁금해하는 것이 당연하다.

명제 3 임의의 위상공간 \(X,Y\)와 commutative ring \(A\)에 대하여,

\[\times: H^*(X;A)\otimes_A H^*(Y;A) \to H^*(X\times Y;A)\]

는 graded \(A\)-algebra homomorphism이다.

증명

즉 우리가 보이고 싶은 것은 다음 diagram

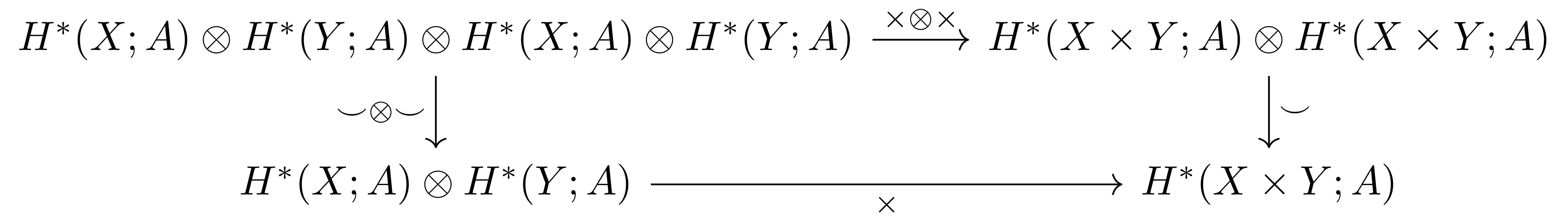
의 commutativity이다. 이는 임의의 \(\alpha_1,\alpha_2\in H^\ast(X;A)\)와 임의의 \(\beta_1,\beta_2\in H^\ast(Y;A)\)에 대하여,

\[(\alpha_1\times\beta_1)(\alpha_2\times\beta_2)=\Delta_{X\times Y}^\ast ((\alpha_1\times\beta_1)\times(\alpha_2\times\beta_2))\]

이고, 이제 우변이 \(\alpha_1\times\beta_1\times\alpha_2\times\beta_2\)의 꼴이므로 이를 다시 적절하게 묶어주면 된다. 이것이 graded homomorphism이고 \(1\)을 보존하는 것은 자명하다.

그럼 이를 바탕으로 cup product의 functoriality 또한 보일 수 있다.

명제 4 연속함수 \(f:X \rightarrow Y\)에 대하여, cohomology functor가 유도하는 \(f^\ast=H^\bullet(f;A):H^\bullet(Y;A)\rightarrow H^\bullet(X;A)\)는 graded \(A\)-algebra들 사이의 morphism이다. 즉, 다음의 식

\[f^\ast(\alpha\smile\beta)=(f^\ast\alpha)\smile(f^\ast\beta)\]

이 성립한다.

이 명제의 증명은 앞선 명제 3에 의해 우리는 다음 diagram

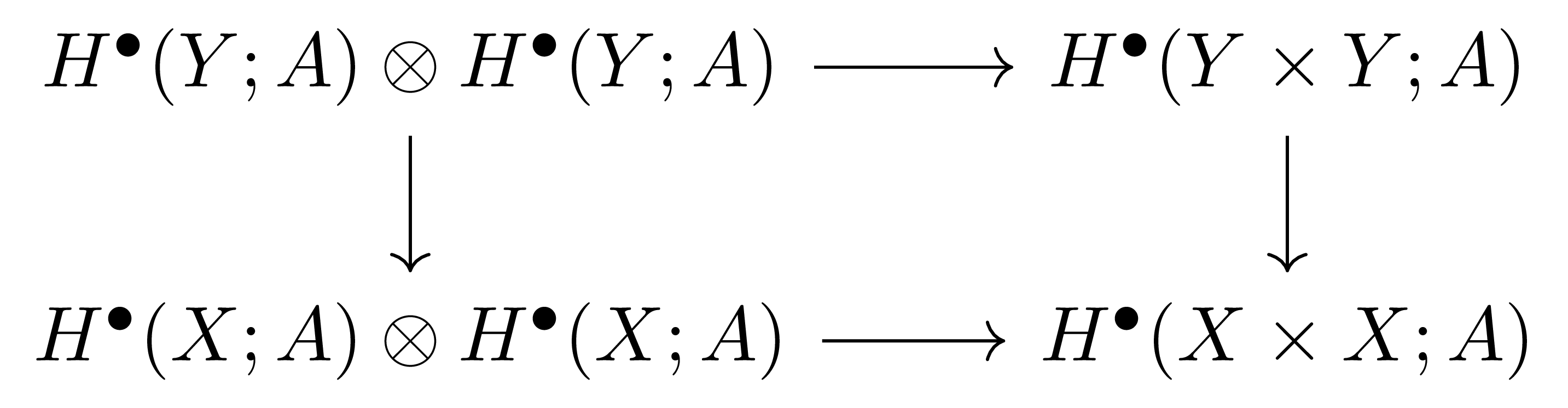
이 commute하는 것을 알고 있으므로, 여기에 더해 다음 diagram

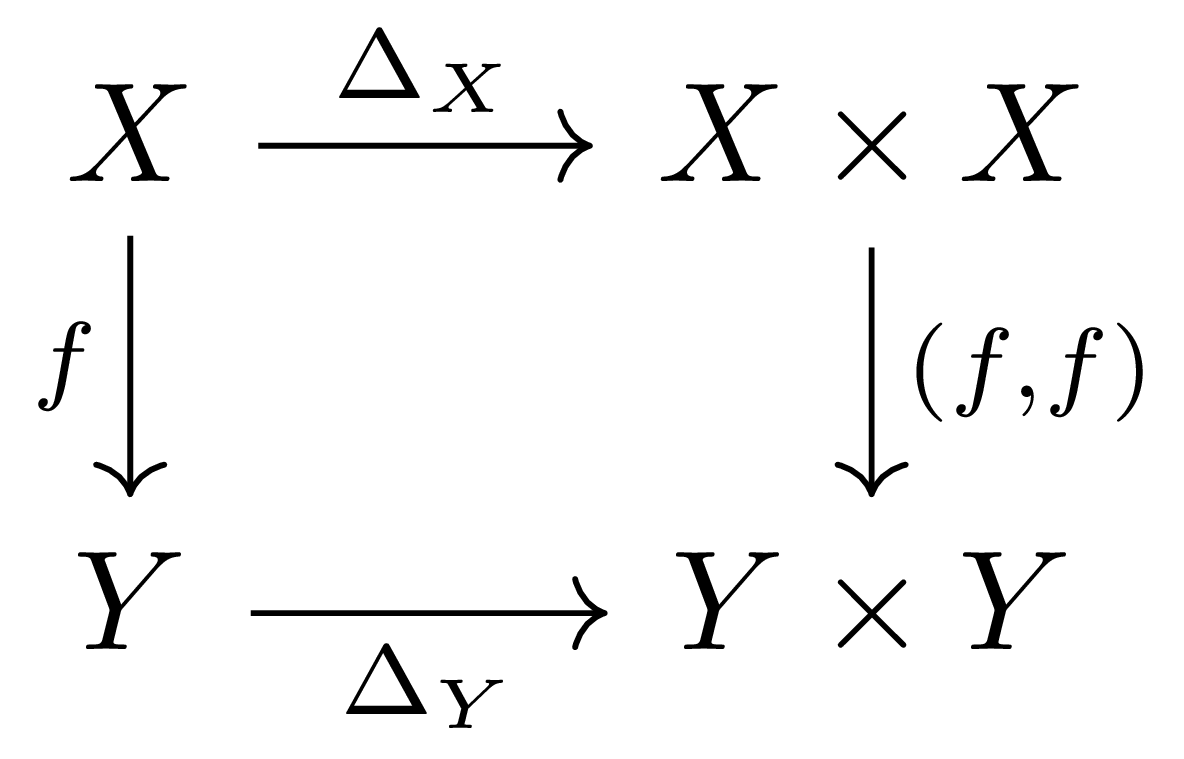
에 cohomology functor를 취해주면 된다.

Cap product

이제 남은 부분에서 우리는 homology와 cohomology의 duality를 다루기 위한 준비를 한다. 물론 우리는 이 duality를 [대수적 위상수학] §코호몰로지, ⁋명제 3와 같은 형태로 관찰할 수 있었지만, 이번에 살펴볼 것은 조금 더 미묘한 감이 있다.

우리가 지금부터 할 일은 homology module \(H_\bullet(X;A)\)에 graded ring \(H^\bullet(X;A)\)의 action을 정의하는 것이다. 이를

\[{\frown}:H^\bullet(X;A)\otimes_A H_\bullet(X;A) \rightarrow H_\bullet(X;A)\]

라 적으면, 우리가 요구하는 \(\frown\)의 성질은 다음의 adjunction formula

\[\langle \alpha\smile\beta,\sigma\rangle=\langle \alpha,\beta\frown \sigma\rangle\]

이며, 이를 통해 \(H_\bullet(X;A)\)는 \(H^\bullet(X;A)\)-module 구조를 갖게 된다. 여기서 \(\langle-,-\rangle\)은 Kronecker pairing

\[\langle-,-\rangle: C^\bullet(X;A)\times C_\bullet(X;A) \rightarrow A\]

가 유도하는 pairing이다. 이제 이 식이 성립하기 위해서는,

\[\langle\alpha,\beta\frown \sigma\rangle=\langle\alpha\smile \beta,\sigma\rangle=\sum_i(-1)^{\lvert\beta\rvert\lvert\sigma_i\rangle}\alpha(\sigma_i)\beta(\tau_i)\]

이어야 한다. 여기서 \(\sigma_i\)와 \(\tau_i\) 각각은 \(\sigma\)를 Alexander-Whitney map을 통해 \(\sum \sigma_i\otimes\tau_i\)로 나타냈을 때 등장하는 chain들이다. 그럼 이 식이 모든 \(\alpha\)에 대해 성립해야 하므로, 우리는

\[\beta\frown \sigma=\sum_i(-1)^{\lvert\beta\rvert\lvert\sigma_i\rvert}\beta(\tau_i)\sigma_i\]

으로 정의해야만 한다.

정의 5 위와 같이 정의된 함수

\[\frown:H^p(X;A)\otimes H_{p+q}(X;A) \rightarrow H_q(X;A)\]

를 cap product라 부른다.

즉 \(\frown\)은 degree \(p+q\)의 homology chain과 degree \(p\)의 cohomology chain을 받아서, homology chain의 degree \(p\)인 부분과 cohomology chain을 Kronecker pairing을 통해 연산한 후, 이 상수를 남아있는 degree \(q\)의 homology chain에 scalar multiplication을 해 주어 얻어지는 것이다. 이는 다소 작위적인 정의로 보일 수 있으나 §Acyclic models theorem, ⁋정리 3의 유일성에 의해 유일하게 말이 되는 정의라 할 수 있다. 뿐만 아니라, 이 표현으로부터 이것이 정확하게 interior product에 해당하는 연산임을 안다.

그럼 다음이 성립한다.

명제 6 (Projection formula) 연속함수 \(f:X \rightarrow Y\)와 \(\alpha\in H^p(X)\), \(\beta\in H^q(Y)\), 그리고 \(\sigma\in H_{p+q}(X)\)에 대하여 다음의 식

\[f_\ast(f^\ast\beta\frown\sigma)=\beta\frown f_\ast\sigma\]

이 성립한다.

---

참고문헌

[Hat] A. Hatcher, Algebraic Topology. Cambridge University Press, 2022.

---