호몰로지

심플렉스

먼저 소개할 심플렉스는 호몰로지 이론을 전개할 때 직관적인 이해에 도움을 준다.

정의 1 임의의 자연수 \(k\)에 대하여, 일반적인 방식으로 배열된 \(k+1\)개의 점 \(v_0,\ldots, v_k\in\mathbb{R}^d\)가 주어졌다 하자. 그럼 이들로 만들어지는 \(k\)-simplex_{\(k\)-심플렉스, \(k\)-단체}는 집합 \(\{v_0,\ldots, v_k\}\)을 포함하는 볼록집합 중 가장 작은 것이다.

여기서 \(k+1\)개의 꼭짓점들이 일반적으로 배열되었다는 것은 이들 점들이 \(k\)차원보다 작은 임의의 초평면에 포함되지 않는 것이다. 바꿔말하면 \(k\)개의 벡터

\[v_1-v_0,\ldots, v_k-v_0\]

이 linearly independent인 것으로도 이해할 수 있다. 예를 들어 \(0\)-simplex는 점이고, \(1\)-simplex는 두 꼭짓점을 잇는 선분, \(2\)-simplex는 세 점을 잇는 삼각형이며 \(3\)-simplex는 사면체이다.

위의 그림과 같이 \(\mathbb{R}^{n+1}\)에서 \(n+1\)개의 꼭짓점들

\[(1,0,\ldots, 0),\qquad\cdots,\qquad (0,0,\ldots,1)\]

로 만들어진 \(n\)-simplex를 standard simplex라 부른다. 당연하게 이들 simplex들은 그 자체로는 우리의 관심대상이 아니며, 우리는 이들을 이용하여 다양체의 불변량을 계산하는 데에 관심이 있다. 이를 위해 우리는 다양체 위에 \(\Delta\)-complex의 구조를 정의해야 하는데, 간단하고 직관적인 예시로 다음을 보자.

예시 2 우리가 종종 생각하게 되는 예시는 (2차원) torus \(T^2\)이다. 이는 간단한 정의로는 product manifold \(S^1\times S^1\)이지만, 직관적으로 이 product manifold가 torus임을 보려면 다음 그림을 생각하면 된다.

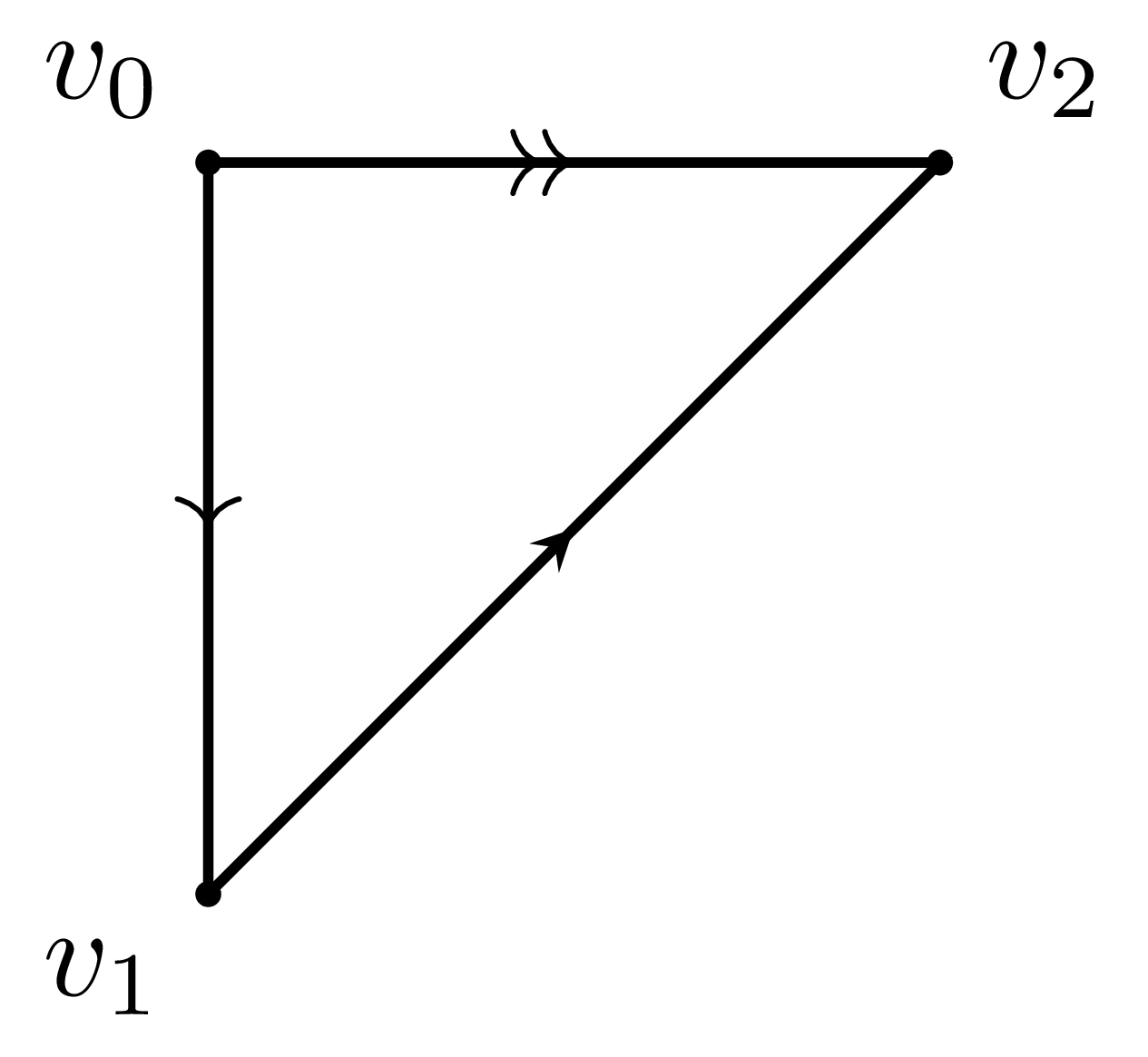
이 그림에서 각 색깔의 선들을 화살표의 방향대로 ‘‘꼬지 않고’’ 붙이는 상상을 해보자. 가령 수평방향의 모서리들을 먼저 붙여 원기둥을 만든 후, 남은 모서리를 따라 원기둥의 밑면을 서로 붙여주면 다음과 같이 될 것이다.

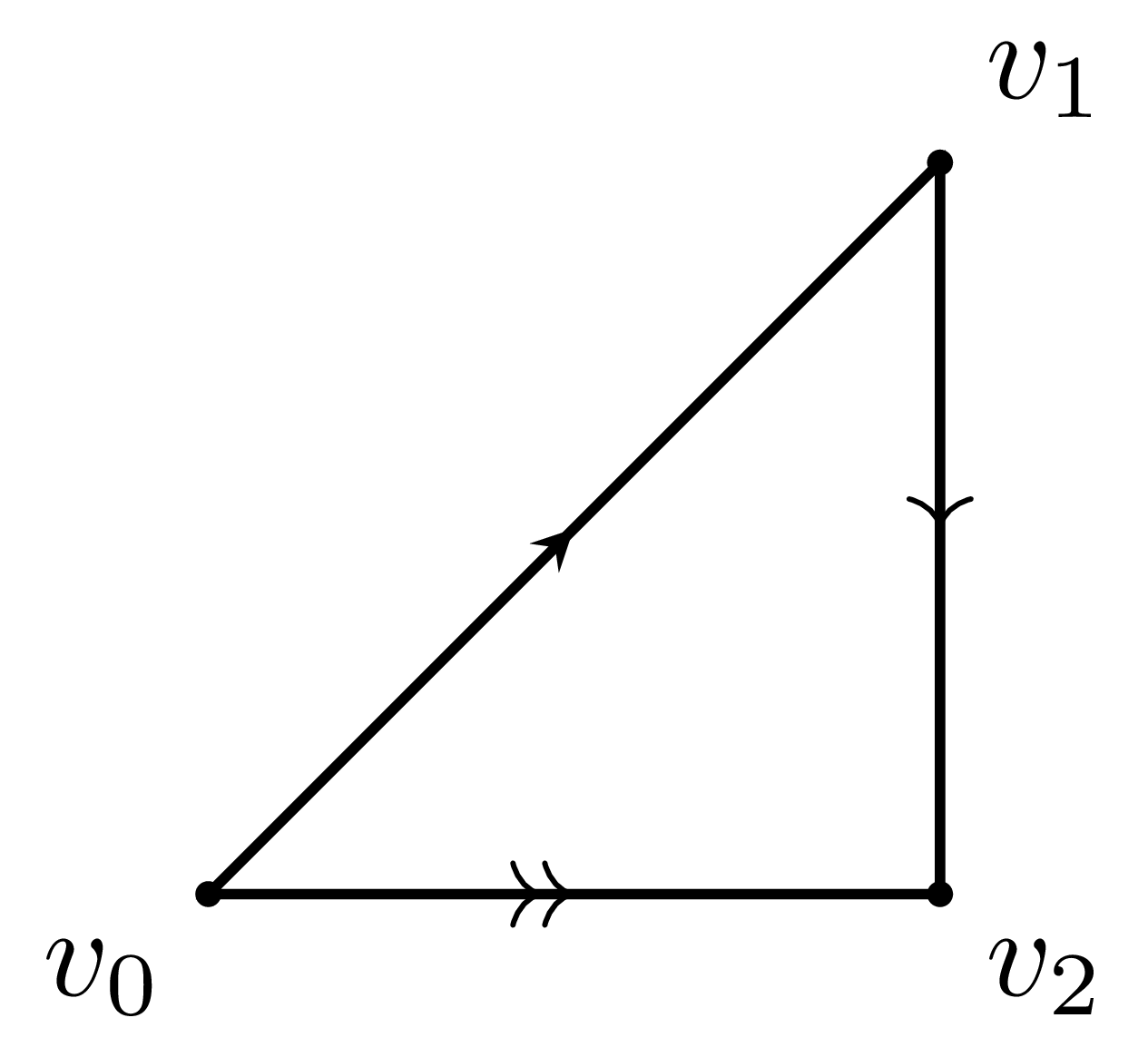
이는, 만일 위의 정사각형이 네 점 \((0,0),(0,1),(1,0),(1,1)\)을 지나는 좌표평면 상의 점이었다 하면 이 정사각형에 다음의 동치관계

\[(x,0)\sim (x,1),\qquad (0,y)\sim(1,y)\]

를 부여하여 얻어지는 quotient space이며 \(S^1\)이 수직선 상의 구간 \([0,1]\)에 \(0\)과 \(1\)을 같은 것으로 보는 quotient topology를 주어 얻어지는 것을 생각하면 위의 정의 \(T^2=S^1\times S^1\)와 같은 것임을 안다. 한편 같은 모양의 그림에, 이번에는 한 변의 방향을 바꾸고 수평방향의 모서리만 붙이는 다음의 quotient space

를 생각하면 이번에 얻어지는 공간은 원기둥이 아니라 뫼비우스 띠

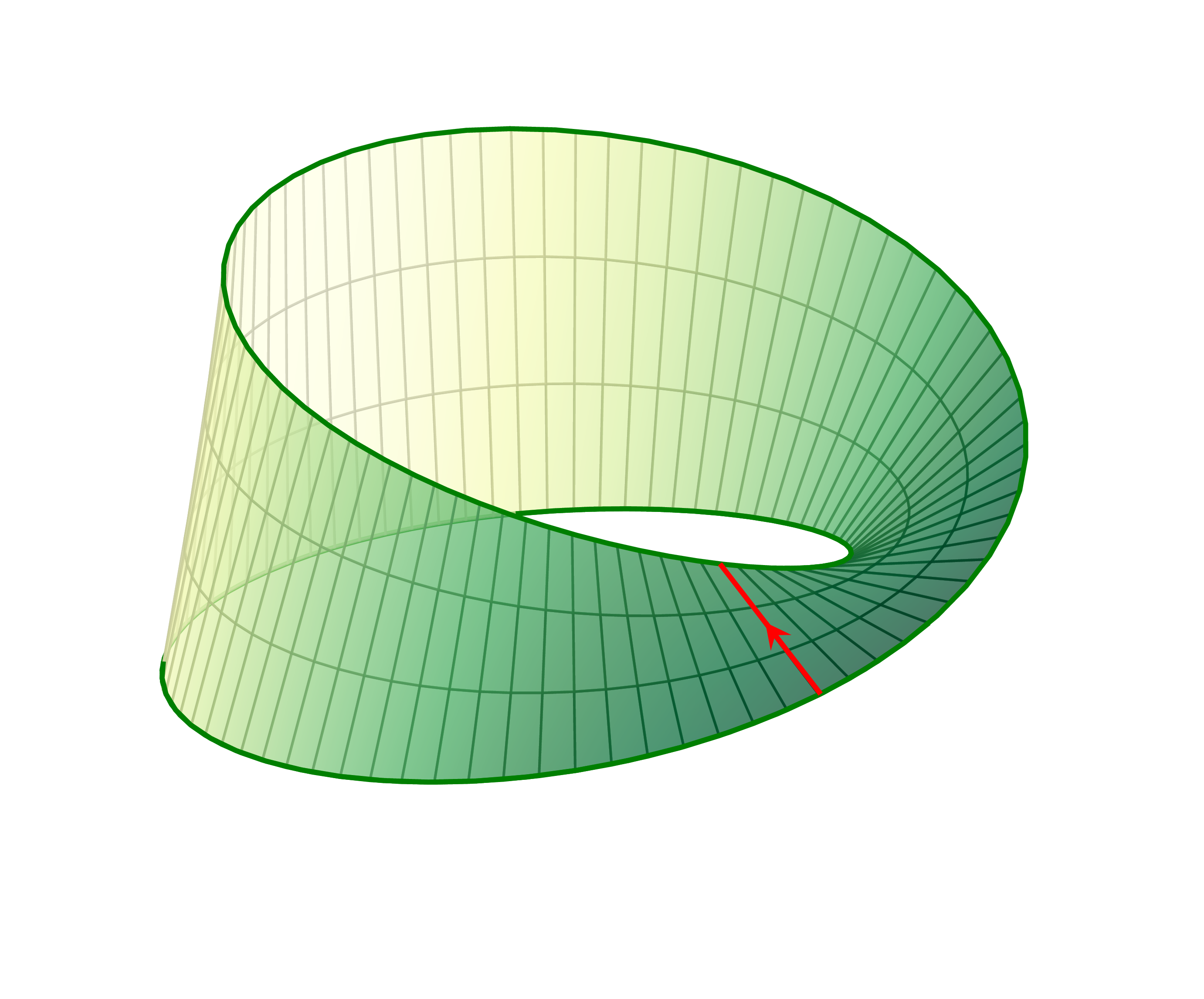
이다.

위의 예시에서, 평면 위에 그려진 사각형들을 대각선을 따라 두 개의 삼각형으로 나누면 이 사각형들은 두 \(2\)-simplex들을 이어붙인 것으로 생각할 수 있고, 이를 위와 마찬가지 방법으로 quotient space 위에 옮겨주면 예시 2의 공간들을 simplex들을 이어붙여 만든 것으로 이해할 수 있다. 이 예시에서 볼 수 있듯 \(2\)-simplex를 붙일 때에는 변의 방향(더 일반적으로, \(n\)-simplex를 붙일 때에는 \((n-1)\)-simplex의 방향)이 중요한데, 이는 꼭짓점들 사이의 total order를 주면 결정된다. 가령, 꼭짓점 \(v_0,\ldots, v_k\)으로 만들어진 \(k\)-simplex를 index의 순서대로 나열된 것을 양의 방향이라 한다면, 여기에서 odd permutation을 취해 얻어지는 \(v_1,v_0,v_2,\ldots,v_k\)는 음의 방향이 되는 식이다. 우리는 이렇게 index 순서에 맞게 향이 주어진 simplex를 \([v_0,\ldots, v_k]\)로 적는다. 이 표기법 하에서, \(k\)-simplex의 한 꼭짓점을 잊어버려 생기는 \((k-1)\)-simplex는 원래의 \(k\)-simplex의 한 면으로 보든, 다음의 \((k-1)\)-simplex

\[[v_0,\ldots,\hat{v}_i,\ldots, v_k]=[v_0,\ldots, v_{i-1},v_{i+1},\ldots, v_k]\]

로 보든 그 방향은 같게 된다.

정의 3 위상공간 \(X\)에 대하여, 이 위에 주어진 \(\Delta\)-complex 구조는 다음과 같이 정의된 함수 \(\sigma_\alpha:\Delta^{n(\alpha)}\rightarrow X\)들의 모임이다.

1. \(\sigma_\alpha\)를 \(\interior(\Delta^{n(\alpha)})\)로 제한한 것이 단사이며, \(X\)의 임의의 점 \(x\)에 대해 \(x\in \sigma_\alpha(\interior(\Delta^{n(\alpha)}))\)를 만족하는 \(\alpha\)가 정확하게 하나 존재한다.
2. \(\sigma_\alpha\)를 \(\Delta^{n(\alpha)}\)의 한 면으로 제한한 \(\sigma_\alpha\vert_{\Delta^{n(\alpha)-1}}:\Delta^{n(\alpha)-1}\rightarrow X\) 또한 이 함수들의 모임에 속한다.
3. \(A\subseteq X\)가 \(X\)에서 열린집합인 것과, 각각의 \(\alpha\)에 대하여 \(\sigma_\alpha^{-1}(A)\)가 \(\Delta^{n(\alpha)}\)에서 열린집합인 것이 동치이다.

가령 standard simplex \(\Delta^2\)는 자명하게 \(\Delta\)-complex 구조를 갖는데, 명시적으로 이 구조를 주는 함수들은

\[\operatorname{id}_{\Delta^2}:\Delta^2\rightarrow\Delta^2\]

와, \(1\)-simplex \(\Delta^1\)을 각 변으로 보내는 세 개의 함수 \(\sigma^1_1,\sigma^1_2,\sigma^1_3\), 그리고 \(0\)-simplex \(\Delta^0\)을 각 꼭짓점으로 보내는 세 개의 함수 \(\sigma_1^0,\sigma_2^0,\sigma_3^0\)으로 이루어진다.

예시 4 예를 들어, 2차원 torus \(T^2\)는 다음의 그림

과 같이 나타날 수 있으며, 이 그림은 동시에 \(T^2\)에 \(\Delta\)-complex의 구조를 준다.

심플렉스 호몰로지

이제 우리는 위에서 정의한 \(\Delta\)-complex 구조를 사용하여 위상공간의 불변량을 정의한다. 더 구체적으로 이는 simplex들의 formal sum들이 이루는 group을 통해 정의될 것이다. 그런데 이쯤에서 지적할 미묘한 문제가 있는데, 이것이 위상공간 \(X\)의 불변량이 되기 위해서는 \(\Delta\)-complex 구조의 선택에 의존하지 않아야 한다는 것이다.

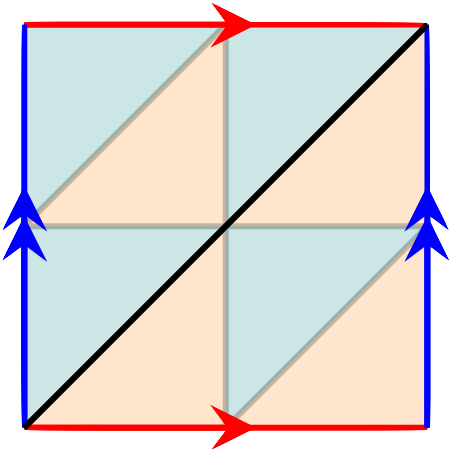
가령 예시 2의 사각형을 더 잘게 쪼개어 위의 그림과 같이 더 많은 2-simplex들을 만들었을 때, 이로부터 새로 생기는 회색 \(1\)-simplex들은 어떠한 방식으로든 서로를 상쇄해야 할 것이다. 즉, \(\Delta\)-complex를 택할 때에는 이들의 방향을 알맞게 맞추어 붙여줘야 하지만, 불변량을 계산할 때는 부호를 반대로 바꾸어 더해주어야 한다. 이를 염두에 두면 다음의 계산이 조금 더 와닿을 것이다.

\(\Delta\)-complex 구조가 주어진 위상공간 \(X\)를 생각하고, \(k\)-simplex들로 생성된 free abelian group \(C^\Delta_k(X)\)를 생각하자. 즉

\[C^\Delta_k(X)=\{\sigma_\alpha:\Delta^{n(\alpha)}\rightarrow X\text{ $k$-simplex}\mid n(\alpha)=k\}\cdot\mathbb{Z}\]

이다. Abelian group을 다룰 때의 convention을 따라 \(C^\Delta_k(X)\)의 연산은 덧셈으로 주어진 것으로 생각한다. 앞서 살펴봤듯, \(k\)-simplex \([v_0,\ldots, v_k]\)의 boundary는 다음 \((k-1)\)-simplex들

\[[v_1,v_2,\ldots, v_k],\quad[v_0,v_2,\ldots, v_k],\quad\cdots,[v_0,v_1,\ldots\hat{v}_i,\ldots,v_k],\quad\cdots,\quad[v_0,v_1,\ldots, v_{k-1}]\]

로 이루어진다. 만일 \([v_0,\ldots, v_k]\)의 boundary를 이들의 합처럼 생각한다면, 우리는 \(C^\Delta_k(X)\)에서 \(\Delta_{k-1}(X)\)로의 함수를 얻는다. 만일 boundary map \(\partial_k\)을 이들 simplex들의 단순한 합이 아니라, 다음의 식

\[\partial_k(\sigma_\alpha|_{[v_0,\ldots,v_k]})=\sum_{i=0}^n(-1)^i\sigma_\alpha|_{[v_0,\ldots, \hat{v}_i,\ldots,v_k]}\tag{1}\]

으로 정의할 경우 \((C^\Delta_k(X),\partial_k)\)가 chain complex를 이룬다는 사실이 잘 알려져 있다. 이 식 우변의 부호는, 위에서 지적했듯, \(X\) 안에서 맞닿아있는 simplex들이 서로를 상쇄하도록 설정된 것이다.

명제 5 \((C^\Delta_k(X),\partial_k)\)는 chain complex이다. ([범주론] §아벨 카테고리, ⁋정의 4)

증명

임의의 \(\sigma_\alpha\in C^\Delta_k(X)\)에 대하여,

\[\partial_k(\sigma_\alpha|_{[v_0,\ldots,v_k]})=\sum_{i=0}^n(-1)^i\sigma_\alpha|_{[v_0,\ldots, \hat{v}_i,\ldots,v_k]}\]

이므로

\[\partial_{k-1}\partial_k(\sigma_\alpha|_{[v_0,\ldots,v_k]})=\sum_{j < i}(-1)^{i+j}\sigma_\alpha|_{[v_0,\ldots, \hat{v}_j,\ldots\hat{v}_i,\ldots,v_k]}+\sum_{j > i}(-1)^{i+j-1}\sigma_\alpha|_{[v_0,\ldots, \hat{v}_i,\ldots\hat{v}_j,\ldots,v_k]}\]

이고, 따라서 첫째 합과 둘째 합이 서로 상쇄되어 사라진다.

이렇게 얻어지는 chain complex \((C^\Delta_k(X),\partial_k)\)의 \(n\)번째 호몰로지를 \(n\)번째 simplicial homology_{\(n\)번째 심플렉스 호몰로지}라 부르고, \(H_n^\Delta(X)\)로 적는다. ([호몰로지 대수학] §호몰로지, ⁋정의 3)

예시 6 2차원 토러스 \(T^2\)를 위의 예시 4과 같이 나타내고, 오른쪽에 나열된 순서대로 \(2\)-simplex를 각각 \(L\), \(U\), \(1\)-simplex를 각각 \(a,b,c\), 그리고 \(0\)-simplex를 \(p\)라 하자. 두 \(1\)-simplex \(b,c\)에는 이미 방향이 주어져 있으므로, 이들이 simplex가 되기 위해서는 \(a\)가 왼쪽 아래에서 오른쪽 위로의 방향을 가져야 한다. 이제

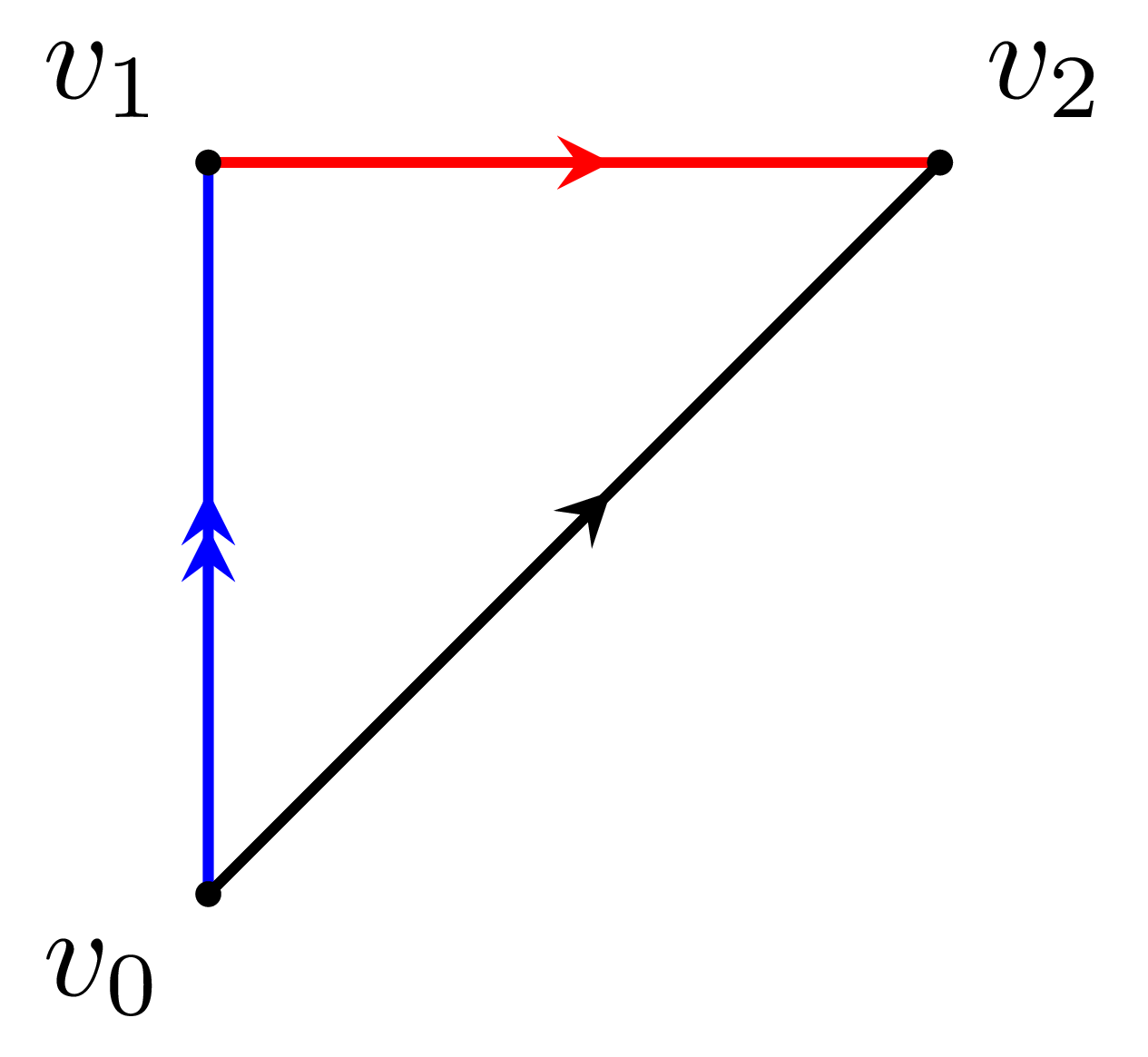
과 같이 \(U\)의 꼭짓점 \(v_0,v_1,v_2\)가 주어졌다 생각하면

\[a=[v_0,v_2],\quad b=[v_1,v_2],\quad c=[v_0,v_1]\]

이라 할 수 있다. 비슷하게, 다음의 그림

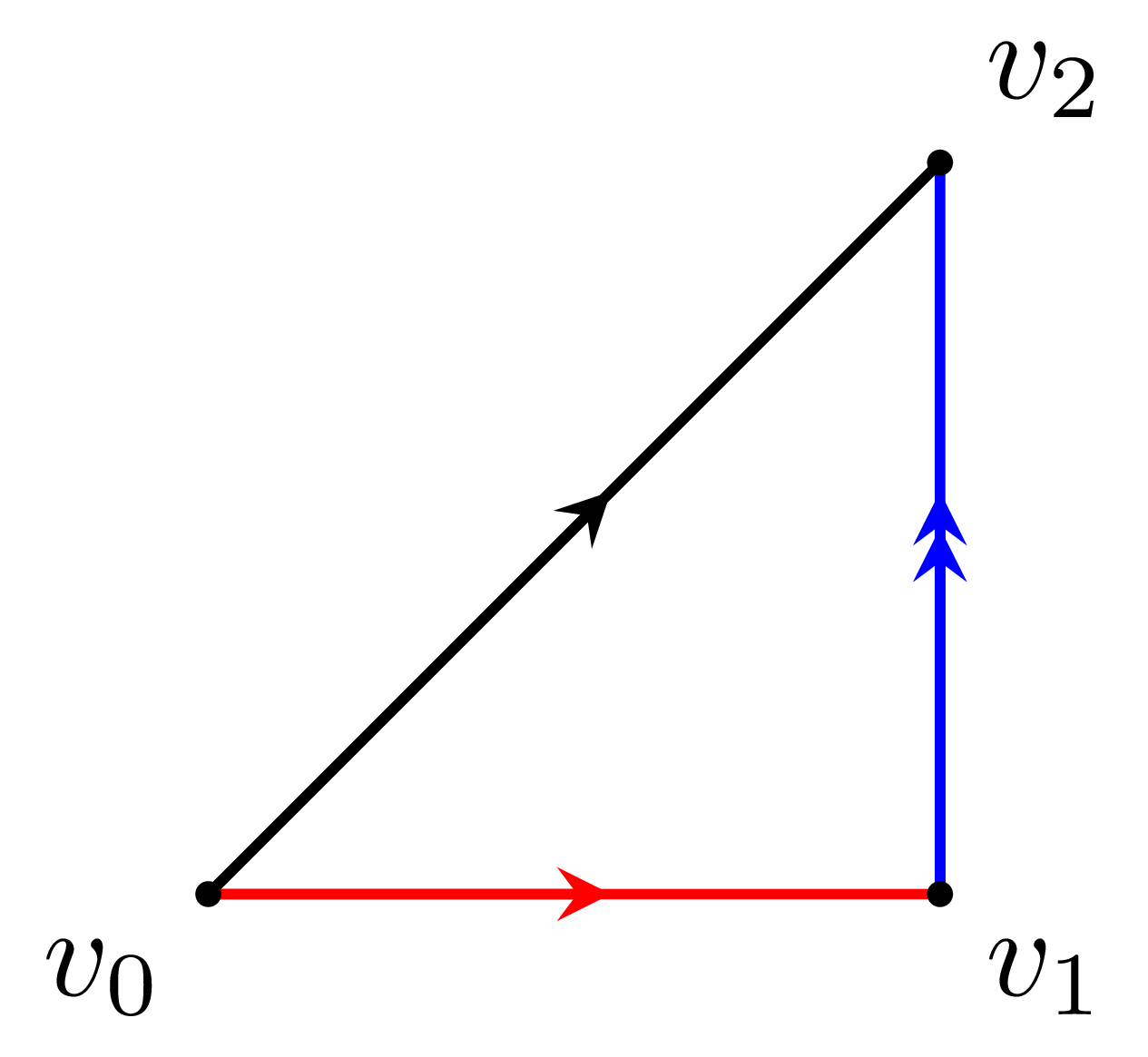
과 같이 \(L\)의 꼭짓점 \(v_0,v_1,v_2\)가 주어졌다 생각하면 \(L\)에서는

\[a=[v_0,v_2],\quad b=[v_0,v_1],\quad c=[v_1,v_2]\]

인 것으로 생각할 수 있다.

이제 boundary map \(\partial_2:C^\Delta_2(T^2)\rightarrow C^\Delta_1(T^2)\)을 생각하면

\[\begin{aligned}\partial_2(U)&=[v_1,v_2]-[v_0,v_2]+[v_0,v_1]=b-a+c,\\ \partial_2(L)&=[v_1,v_2]-[v_0,v_2]+[v_0,v_1]=c-a+b\end{aligned}\]

이다. 또, \(\partial_1:C^\Delta_1(T^2)\rightarrow C^\Delta_0(T^2)\)을 생각하면 이들 꼭짓점들은 모두 \(T^2\)에서는 같은 점 \(p\)에 대응되므로

\[\partial_1(a)=\partial_1(b)=\partial_1(c)=p-p=0\]

가 되고, 따라서 다음 complex

\[\cdots\overset{\partial_3}{\longrightarrow}C^\Delta_2(T^2)=\langle L,U\rangle\overset{\partial_2}{\longrightarrow}C^\Delta_1(T^2)=\langle a,b,c\rangle\overset{\partial_1}{\longrightarrow}C^\Delta_0(T^2)=\langle p\rangle\overset{\partial_0}{\longrightarrow}0\]

에서

\[\ker\partial_2=\langle L-U\rangle,\qquad\ker\partial_1=C^\Delta_1(T^2),\qquad\ker\partial_0=C^\Delta_0(T^2)\]

그리고

\[\im\partial_3=0,\qquad\im\partial_2=\langle a-b-c\rangle,\qquad \im\partial_1=0\]

이므로

\[H_2^\Delta(T^2)=\ker\partial_2/\im\partial_3\cong\mathbb{Z},\quad H_1^\Delta(T^2)=\ker\partial_1/\im\partial_2\cong \mathbb{Z}\oplus\mathbb{Z},\quad H_0^\Delta(T^2)=\ker\partial_0/\im\partial_1\cong\mathbb{Z}\]

이고, 나머지 호몰로지는 전부 \(0\)이다.

한편 우리는 [호몰로지 대수학] §호몰로지, ⁋정의 3에서, \(Z_n(C)=\ker\partial_n\)의 원소들을 \(n\)-cycle, \(B_n(C)=\im\partial_{n+1}\)의 원소들을 \(n\)-boundary들이라 불렀는데 이제 그 이름들이 직관적으로 명확하다. 즉 이 경우 boundary map들은 실제로 simplex의 경계면을 계산하는 것이며, \(n\)-cycle들은 이렇게 경계면을 계산했을 때 그 값이 상쇄되는 것들, 가령 예시 6에서는 \(a,b\)(와 \(c\))가 원래의 공간 \(T^2\)에서 이루는 폐곡선과 같은 것들을 의미하며 \(n\)-boundary들은 말 그대로 어떠한 \((n+1)\)-simplex의 boundary로서 나타나는 \(n\)-simplex들을 의미한다.

특이 호몰로지

위에서 정의한 심플렉스 호몰로지는 직관적으로 명확한 의미를 갖지만, 임의의 위상공간이 주어졌을 때 \(X\)의 호몰로지를 계산하기 위해서는 이 위에 \(\Delta\)-complex 구조를 주어야 한다는 점에서 그 한계가 명확하다. 설령 \(X\)가 topological manifold라 하여도 그 차원이 \(4\) 이상이면 \(X\) 위에 \(\Delta\)-complex 구조를 주는 것이 불가능할 수도 있다는 것이 잘 알려져 있다.

때문에 우리는 이 조건을 완화하여 새로운 호몰로지를 정의한다.

정의 7 \(X\)에 정의된 singular \(k\)-simplex_{특이 \(k\)-심플렉스}는 연속함수 \(\sigma:\Delta^k\rightarrow X\)를 뜻한다.

앞선 글에서 정의했던 \(\Delta\)-complex 구조와는 다르게, singular \(k\)-simplex들은 \(X\) 안에서 \(k\)-simplex의 모양을 유지할 필요가 전혀 없다. 예를 들어, \(\Delta^k\)의 모든 점을 하나의 점으로 보내는 constant 또한 singular \(k\)-simplex가 된다.

이제 \(C_k(X)\)를 모든 singular \(k\)-simplex들로 생성된 free abelian group이라 하고, \(\partial_k:C_k(X)\rightarrow C_{k-1}(X)\)를 위의 식 (1)과 동일한 방식으로 정의하자. 그럼 정확히 명제 5과 같은 방식으로 \((C_k(X), \partial_k)\)가 chain complex가 된다는 것을 확인할 수 있으며, 이 때의 homoloogy들을 singular homology라 부르고 \(H_n(X)\)로 적는다.

예시 8 Singular homology를 정의로부터 계산하는 것은 좋은 생각이 아니지만, 우리의 직관을 위해 약간의 (엄밀하지 않은) 계산을 해 보자.

정의에 의해 임의의 위상공간 \(X\) 위에서의 singular \(0\)-simplex는 \(\Delta^0\)에서 \(X\)로의 연속함수이다. 그런데 \(\Delta^0\)은 그냥 한 점일 뿐이므로 \(C_0(X)\)는 \(X\)의 점들로 생성되는 free abelian group이다. 비슷하게 \(\Delta^1\)을 구간 \(I=[0,1]\)과 identify하면 \(C_1(X)\)는 그냥 \(X\)에서의 path로 생성되는 free abelian group에 불과하며, 이 때 우리는 constant path \([0,1]\rightarrow X\) 또한 허용하게 되며 이러한 이유로 우리는 이를 singular \(1\)-simplex라 부른다. 마찬가지로 연속적인 변형을 거치면 \(C_2(X)\)는 \(X\) 안에 들어있는 원판들로 생성되는 free abelian group이 될 것이다.

그럼 path \(\sigma:[0,1]\rightarrow X\)의 boundary는 앞선 식 (1)에 따라 \(\partial_1\sigma=\sigma(1)-\sigma(0)\)으로 주어지며 이로부터

\[Z_1(X)=\ker\partial_1=\left\{\sigma:[0,1]\rightarrow X\mid \sigma(1)=\sigma(0)\right\}\]

임을 안다. 즉 직관적으로 \(Z_1(X)\)는 \(X\)에서의 폐곡선들로 생성되는 subgroup이라 생각할 수 있다. 비슷하게 \(B_1(X)=\im\partial_2\)에 기하학적인 의미를 부여해보자면 이는 \(X\)에서의 폐곡선 중 어떠한 원판의 경계로 나오는 것을 의미하며 따라서 첫 번째 호몰로지

\[H_1(X)=\frac{Z_1(X)}{B_1(X)}\]

는 \(X\)에서의 폐곡선 중, 원판의 경계로 나오지 않는 것들이 얼마나 존재하는지를 살펴보는 것이다. 가령 \(\mathbb{R}^2\)의 부분집합

\[D^2=\left\{(x,y)\in \mathbb{R}^2\mid x^2+y^2\leq 1\right\}\]

의 첫 번째 호몰로지는 \(0\)이다. 이는 \(D^2\) 안에서의 어떠한 폐곡선이 주어지든 그 내부를 채우는 방법이 자명하게 존재하기 때문이다.

반면 공간 \(D^2\setminus {(0,0)}\)의 첫 번째 호몰로지는 \(0\)이 아니다. 가령 다음의 폐곡선

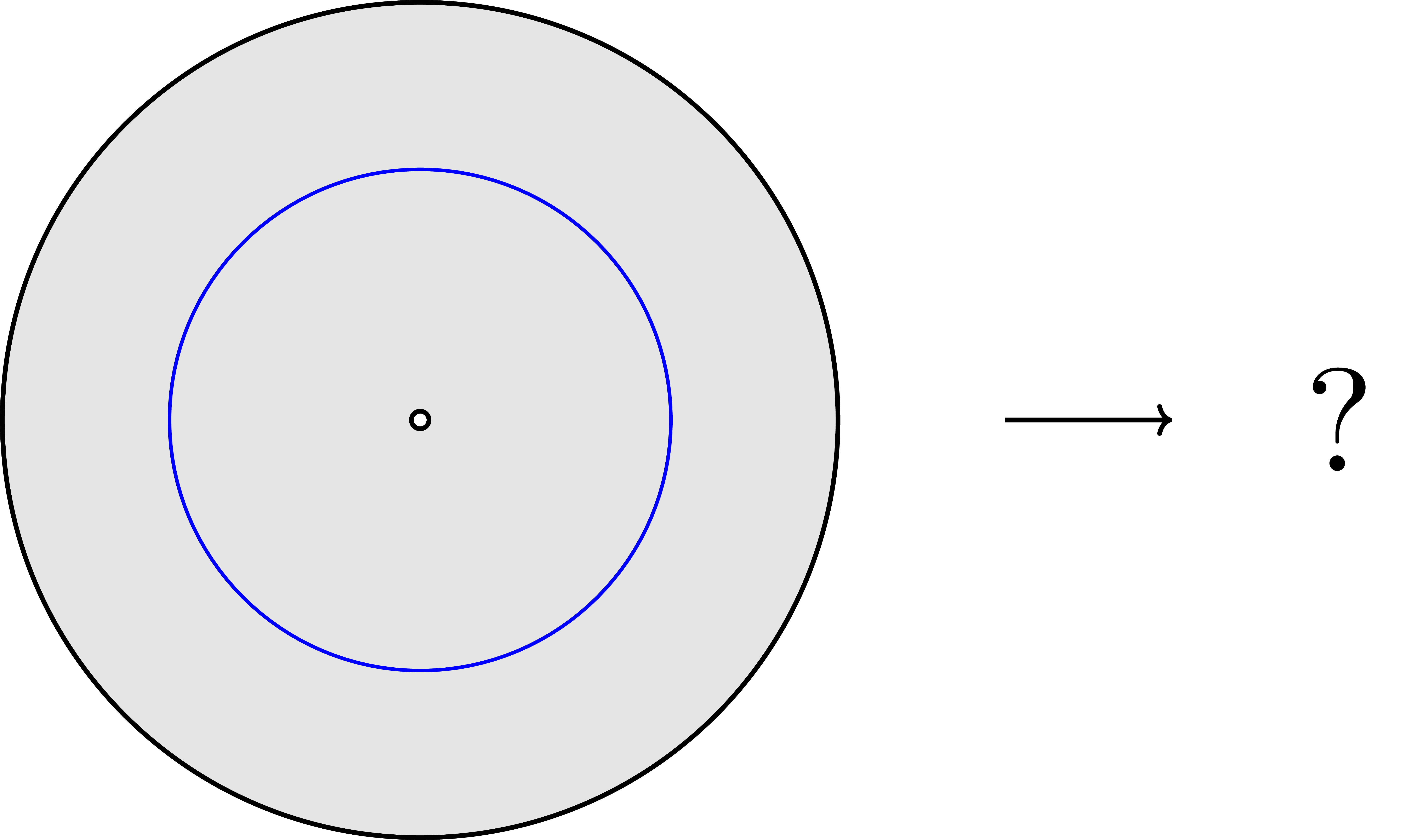
을 생각하면 이 내부를 (연속적으로) 메워 이를 원판으로 만드는 방법이 존재하지 않기 때문이다. 그러나 마찬가지로 구멍이 뚫린 다음의 공간

\[D^3\setminus \left\{(0,0,0)\right\}=\left\{(x,y,z)\in \mathbb{R}^3\mid 0< x^2+y^2+z^2\leq 1\right\}\]

을 생각하면 이 공간의 첫 번째 호몰로지는 \(0\)인데, 이는 “구멍을 포함하는” 폐곡선

\[S^1=\left\{(x,y,0)\in \mathbb{R}^3\mid x^2+y^2=1\right\}\]

이 주어지더라도

와 같이 이를 원판의 경계선으로 볼 수 있기 때문이다. 그 대신, 이 공간의 두 번째 호몰로지는 \(0\)이 아닐 것이다.

이 계산에는 약간의 사소한 갭이 있다. 가령 \(\Delta^1\)의 모든 점을 고정된 \(x\in X\)로 보내는 constant map은 정의에 의해 singular \(1\)-complex이지만, 우리가 \(D^2\)의 임의의 폐곡선을 채울 수 있다고 주장할 때 이와 같은 형태의 (constant) path는 고려하지 않았기 때문이다. 그런데 우리가 보여야 할 것은 결국, 적당한 singular \(2\)-complex \(\Delta^2 \rightarrow X\)에 \(\partial\)을 취하면 이 singular \(1\)-complex가 나온다는 것이므로, 그냥 \(\Delta^2\)의 모든 점을 고정된 \(x\in X\)로 보내는 \(2\)-complex를 생각한 후 이 complex의 boundary를 생각하면 정확히 이것이 우리가 원하는 complex \(\Delta^1 \rightarrow X\)가 된다. 이를 일반화하면 임의의 \(n\)에 대하여, \(\Delta^n\)의 모든 점을 고정된 \(x\in X\)로 보내는 singular \(n\)-complex는 \(\Delta^{n+1}\)의 모든 점을 고정된 \(x\in X\)로 보내는 singular \((n+1)\)-complex의 boundary이다. 다른 말로 하면, constant map은 항상 \(H_n(X)\)의 identity가 된다.

이러한 종류의 갭은 위와 같이 약간의 주의를 기울이면 해결할 수 있는 것이다. 사실 \(\Delta\)-complex 구조를 줄 수 있는 임의의 공간 \(X\)에 대하여 singular homology \(H_n(X)\)와 simplicial homology \(H_n^\Delta(X)\)가 항상 같다는 것을 보일 수 있으며, 이는 대략적으로 이야기하면 constant map과 같이 singular한 \(\Delta^k \rightarrow X\)들은, 마찬가지로 singular한 \(\Delta^{k+1}\rightarrow X\)의 boundary가 되어, 다음의 두 quotient

\[H_n^\Delta(X)=\frac{\ker\partial_n^\Delta}{\im\partial_{n+1}^\Delta},\qquad H_n(X)=\frac{\ker\partial_n}{\im\partial_{n+1}}\]

를 비교했을 때, singular한 \(\Delta^k \rightarrow X\)들을 허용함으로써 \(\ker \partial_n\)이 \(\ker\partial_n^\Delta\)에 비해 커지는만큼 \(\im\partial_n\)도 따라서 커져서 결과적으로 이를 두 quotient가 같게 되는 것이다.

조금 더 본질적인 문제는 이 계산이 전적으로 우리의 기하학적 직관에 의존한다는 것으로, 복잡한 공간의 호몰로지를 구하기 위해서 우리는 조금 더 호몰로지의 일반적인 성질을 공부해야 한다.

호몰로지의 성질들

명제 9 위상공간 \(X\)를 path-component들의 disjoint union \(X=\coprod X_i\)로 나타냈을 때, 다음의 isomorphism

\[H_n(X)\cong \bigoplus_{i\in I} H_n(X_i)\]

이 성립한다.

증명

우선 path-connected space \(\Delta^k\)의 continuous image는 path-connected이므로 singular simplex들의 image는 \(X_i\)들에 온전히 들어있다. 이로부터 \(C_n(X)\cong \bigoplus_{i\in I} C_n(X_i)\)임을 안다. 이 때 마찬가지 이유로 \(\partial\)들 또한 이 decomposition을 보존하며, direct sum은 이러한 map의 kernel과 image를 보존하므로 원하는 결과를 얻는다.

따라서 임의의 위상공간의 homology를 계산하는 것은 임의의 path-connected space의 homology를 계산하는 문제로 귀결된다. 그러나 이 또한 여전히 쉬운 문제는 아니다. 일반적인 경우의 계산은 할 수 없지만, \(n=0\)인 경우는 기하학적인 의미가 있다.

명제 10 Non-empty path-connected space \(X\)에 대하여 \(H_0(X)\cong \mathbb{Z}\)이다.

증명

우선 \(\partial_0=0\)이므로

\[H_0(X)=\ker\partial_0/\im\partial_1=C_0/\im\partial_1\]

이다. Isomorphism \(H_0(X)\rightarrow\mathbb{Z}\)를 만들기 위해 homomorphism \(\varepsilon:C_0(X)\rightarrow\mathbb{Z}\)를 다음의 식

\[\varepsilon\left(\sum n_i\sigma_i\right)=\sum_i n_i\]

로 정의하자. 그럼 \(X\)가 nonempty이므로 \(\varepsilon\)은 surjective이다. 따라서 first isomorphism theorem에 의하여 \(\ker\varepsilon=\im\partial_1\)을 보이면 충분하다. 이 때 \(\ker\varepsilon\)이 \(\im\partial_1\)을 포함하는 것은 \(\partial_1\)의 정의에 의해 자명하므로, 반대방향 포함관계만 보이면 충분하다. \(\varepsilon\left(\sum n_i\sigma_i\right)=0\)이라 가정하고, 각각의 \(i\)에 대하여 \(0\)-simplex \(\sigma_i\)들의 image를 \(x_i\)라 하자. 그럼 \(X\)가 path-connected라는 가정으로부터 적당한 점 \(x\)을 잡아 \(x\)부터 각각의 \(x_i\)로의 path들을 잡을 수 있고, 이들은 이 방향에 따라 \(1\)-simplex들 하나를 결정한다. 이들을 각각 \(\tau_i\)들이라 하면, \(\partial \tau_i=\sigma_i-\sigma\)이고 따라서

\[\partial\left(\sum_i n_i\tau_i\right)=\sum n_i\sigma_i-\sum n_i \sigma=0\]

이므로 이로부터 원하는 결과를 얻는다.

증명은 엄밀성을 위해 다소 길어졌으나, 본질적인 아이디어는 path-connected space \(X\)의 임의의 두 점은 path로 연결 가능하고, 이 path를 \(1\)-simplex로 보면 이들 두 점은 \(1\)-simplex의 boundary가 되므로 \(B_0(X)=\im\partial_1\)에 대해서는 이들 두 점을 같게 볼 수 있다는 것이다.

반대로 모든 \(n\)에 대하여 그 homology를 구할 수 있는 경우도 있는데, \(X\)가 point인 경우이다. 이 경우, \(k\)의 값에 관계없이 singular \(k\)-simplex \(\sigma_k:\Delta^k \rightarrow X\)는 유일하게 (즉, 상수함수로) 결정되고, 이 때 식 (1)을 생각하면 \(\partial_k\)는 \(k\)가 흘수일 때는 \(0\)이고 짝수일 때는 \(\sigma_k\)를 \(\sigma_{k-1}\)로 보낸다. 즉 다음의 chain complex

\[\cdots\rightarrow \mathbb{Z} \overset{0}{\longrightarrow}\mathbb{Z}\overset{\approx}{\longrightarrow} \mathbb{Z}\overset{0}{\longrightarrow}\mathbb{Z}\rightarrow0\]

가 singular simplex들의 chain complex이고, 따라서 다음을 얻는다.

명제 11 One-point space \(X\)에 대하여, \(H_0(X)\cong \mathbb{Z}\)이고 모른 \(k>0\)에 대해서는 \(H_k(X)\cong 0\)이다.

그러나, 물론, 가장 중요하다고 할 수도 있는 성질은 functoriality일 것이다. 그런데 우리는 이미 \(\Ab\)들의 chain complex들의 category \(\Ch_{\geq 0}(\Ab)\)에서, 각각의 \(n\)에 대하여 \(n\)번째 호몰로지를 계산하는 \(H_n:\Ch_{\geq 0}(\Ab)\rightarrow \Ab\)는 functor임을 안다. 따라서 합성

\[\Top \rightarrow \Ch_{\geq 0}(\Ab)\rightarrow \Ab\]

이 functor임을 보이기 위해서는 \(\Top \rightarrow \Ch_{\geq 0}(\Ab)\)이 functor임을 보이면 충분하다.

명제 12 \(\Top\rightarrow\Ch_{\geq 0}(\Ab)\)는 functor이다.

증명

즉 임의의 연속함수 \(f:X\rightarrow Y\)에 대하여 chain map \(C_\bullet(f):C_\bullet(X)\rightarrow C_\bullet(Y)\)가 존재함을 보여야 한다. 당연히 \(C_\bullet(f)\)는 다음의 식

\[C_\bullet(f):\sigma\mapsto f\circ\sigma\]

로 정의하면 되고, 핵심은 이것이 chain map임을 보이는 것이다. 이것이 chain map인 것은 임의의 \(\sigma:\Delta^n \rightarrow X\)에 대하여,

\[\begin{aligned}(C_\bullet(f)\circ\partial^X_n)(\sigma)&=C_\bullet(f)\left(\sum_{i=0}^n(-1)^i\sigma\vert_{[v_0,\ldots,\hat{v}_i,\ldots,v_n]}\right)=\sum_{i=0}^n(-1)^iC_\bullet(f)(\sigma\vert_{[v_0,\ldots,\hat{v}_i,\ldots,v_n]})\\&=\sum_{i=0}^n(-1)^i f\circ(\sigma\vert_{[v_0,\ldots,\hat{v}_i,\ldots,v_n]})=\sum_{i=0}^n(-1)^i (f\circ\sigma)\vert_{[v_0,\ldots,\hat{v}_i,\ldots,v_n]}\\&=\partial_n^Y(f\circ\sigma)=(\partial_n^Y\circ C_\bullet(f))(\sigma)\end{aligned}\]

이므로 간단하게 증명된다.

마지막으로 다음을 정의한다.

정의 13 만일 임의의 \(n\)에 대하여 \(H_n(X)\cong H_n(Y)\)이 성립한다면, 두 공간 \(X,Y\)가 homologous하다 말한다.

---

참고문헌

[Hat] A. Hatcher, Algebraic Topology. Cambridge University Press, 2022.

---