특성류

이전 글에서 중요한 역할을 했던 $p:\Spe(\or_M^A)\rightarrow M$은 covering space로, 이들은 다음과 같은 성질을 가지고 있었다.

1. 임의의 $x\in M$에 대하여, $p^{-1}(x)\cong \{x\}\times A^\times$이다.
2. 뿐만 아니라, 임의의 $x\in M$에 대하여, 적당한 열린집합 $U$가 존재하여 $p^{-1}(U)\cong U\times A^\times$이다.

이제 우리는 이를 더 일반화하여 $p^{-1}(x)$ 위에 (discrete set이 아닌) 추가적인 구조가 있는 경우를 살펴본다. 가장 일반적인 정의는 다음과 같다.

정의 1 위상공간 사이의 contiuous surjection $p:E \rightarrow B$, 그리고 위상공간 $F$에 대하여 fiber bundle_올다발이라는 것은 각각의 $x\in B$마다 열린집합 $U$가 존재하여, 다음의 diagram

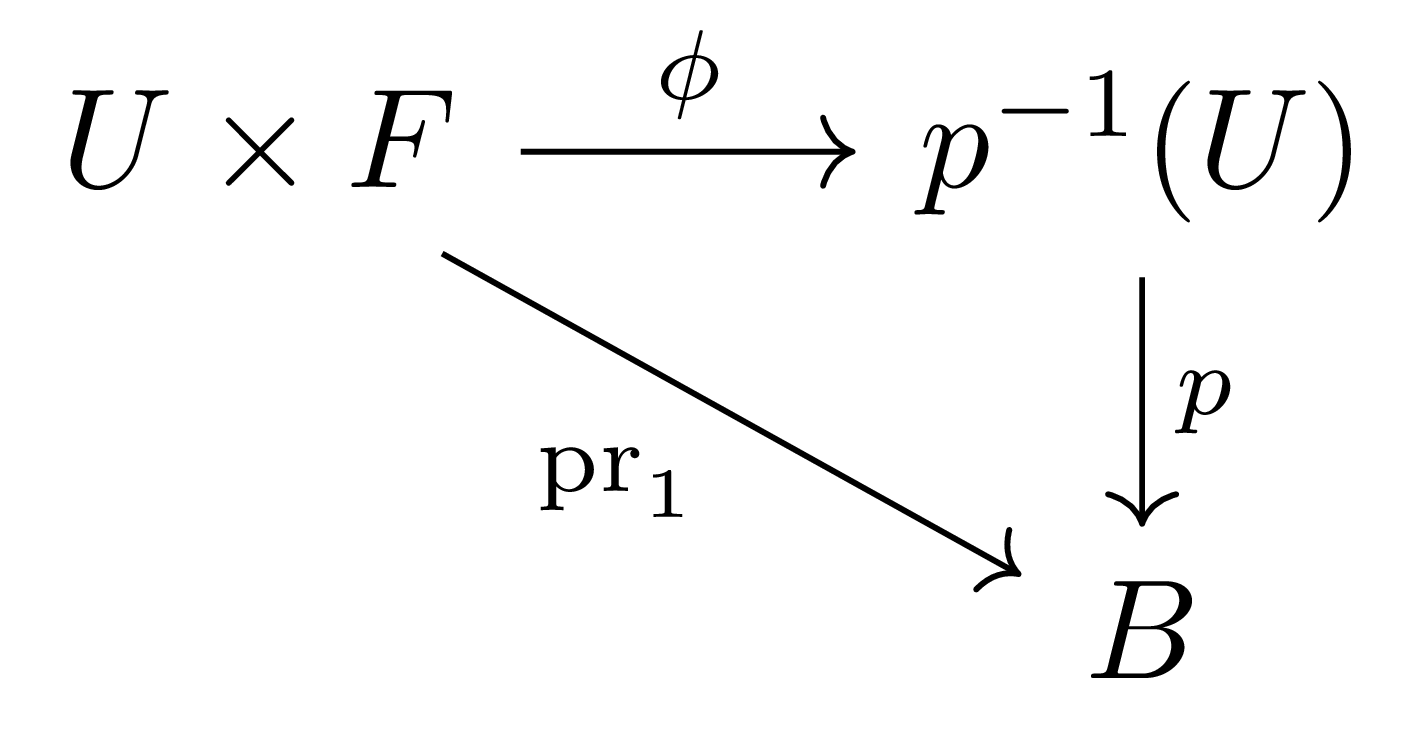
을 commute하게 하는 homeomorphism $\phi:U\times F\rightarrow p^{-1}(U)$가 존재하는 것이다.

이 때, $B$는 이 bundle의 base space, $E$는 total space, $F$는 fiber라 칭하며, 만일 $U=B$로 택할 수 있으면 이 fiber bundle을 trivial bundle이라 부른다. 가령 앞선 예시에서 $M$이 base space, $\Spe(\or_M^A)$는 total space이며 discrete topology가 주어진 $A^\times$가 fiber가 된다. 더 일반적으로 임의의 covering space는 그 fiber가 discrete topology가 부여된 fiber bundle이라 할 수 있다.

특별히 우리가 관심을 가지는 경우는 fiber $F$가 벡터공간일 경우와, topological group일 경우의 두 가지이다. 편의상 앞으로 $B$는 connected인 것으로 가정한다.

벡터다발

우선 우리는 $F$가 벡터공간일 경우를 생각한다. Fiber $F$가 topological group일 경우, $F$는 이미 위상구조가 부여되어 있으므로 정의 1에서 product space $U\times F$의 위상구조가 명확하지만 벡터공간일 경우는 다소 애매하다. 가장 일반적인 세팅으로는 topological ring $\mathbb{K}$이 작용하는 topological vector space $V$념을 사용하면 되지만, 우리는 편의를 위해 당장은 $F$의 base field가 $\mathbb{R}$이고, $F$는 canonical inner product로부터 오는 metric topology가 부여된 공간인 경우만 생각하기로 한다.

정의 2 Fiber bundle $p:E \rightarrow B$에 대하여, fiber space $F$가 위와 같이 위상구조가 주어진 $\mathbb{R}$-벡터공간이고, 추가로 임의의 $x\in B$와, 정의 1의 homeomorphism $\phi:U\times F\rightarrow p^{-1}(U)$에 대하여 다음의 함수

\[\phi(x,-):F \rightarrow p^{-1}(x);\qquad v\mapsto \phi(x,v)\]

가 벡터공간 사이의 isomorphism인 것이다.

이를 통해 각각의 fiber $p^{-1}(x)$에는 $F$로부터 물려받는 vector space 구조가 정의된다. 일반적으로 두 vector bundle $p_1:E_1 \rightarrow B_1$과 $p_2:E_2\rightarrow B_2$가 주어졌을 때, 이들 사이의 morphism은 연속함수들의 commutatuve diagram

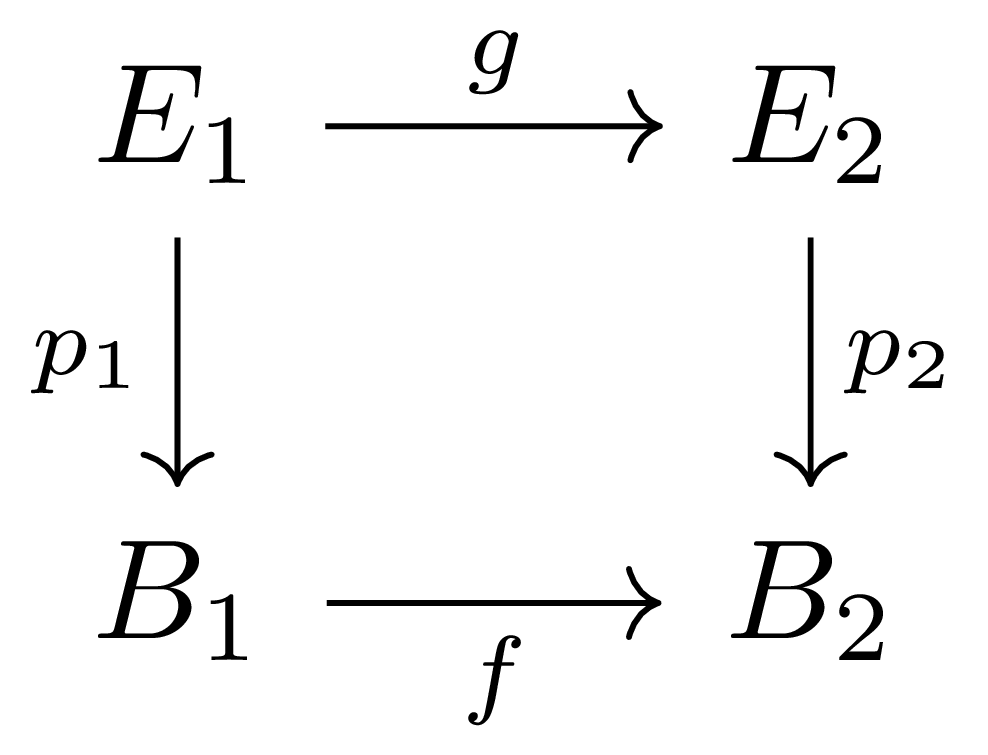
을 의미한다. 단, 여기에서 $g$를 각각의 $x\in B_1$에 대하여 $p^{-1}(x)\rightarrow p_2^{-1}(f(x)))$로 제한하였을 때 이 함수가 벡터공간들 사이의 linear map이 되어야 한다. Vector bundle들 사이의 isomorphism을 어떻게 정의해야 하는지는 자명하다.

한편 위의 정의 2에서, 우리는 $F$가 $\mathbb{R}$-벡터공간인 경우만 생각하여, $\mathbb{R}^n$ 위에 정의된 inner product 구조와 $\mathbb{R}$의 위상구조를 사용하여 이 위에 위상구조를 정의했다. 하지만 엄밀히 말하자면 여기서 필요한 정보는 오직 vector space $F$의 위상구조 뿐으로, $F$를 inner product space로 보았을 때 이는 Euclidean bundle이라 부른다. 어쨌든 우리는 대체로 $\mathbb{R}$-벡터공간만 생각할 것이므로 이러한 차이는 넘어가기로 한다.

예시 3 Trivial bundle이 아닌 예시로는 뫼비우스 띠의 orientation double cover가 있다. 한편 §푸앵카레 쌍대성, ⁋예시 3에서 우리는 $S^1$의 non-trivial cover또한 생각했었는데, 이는 다음과 같이 기하학적으로 일반화할 수 있다.

$n+1$차원 벡터공간 $\mathbb{R}^{n+1}$에 대하여, 원점을 지나는 직선들의 공간을 우리는 projective $n$-space라 부르고 $\RP^n$으로 표기한다. 원점을 지나는 직선 위의 점들 중, 원점까지의 거리가 $1$인 두 점은 같은 직선을 지정하므로, 우리는 이를 unit $n$-sphere $S^n$ 위의 antipodal point들을 identify하여 얻어지는 quotient space로 생각할 수 있다.

이제 이 공간 $\RP^n$을 base space $B$로 두고, 이 위에 정의된 vector bundle $E(\gamma_n^1)$를 다음과 같이 정의하자. 집합으로서

\[E(\gamma_n^1)=\{((x,v)\in \RP^n\times \mathbb{R}^{n+1}\mid x\in \span(x)\}\]

으로 정의되며, projection $\gamma_n^1:E(\gamma_n^1)\rightarrow \RP^n$는 첫 번째 좌표로의 projection이다. 즉 $\gamma_n^1$는 각 점 $x\in \RP^n$마다, $x$가 원래 $\mathbb{R}^{n+1}$에 있을 때 속해있던 바로 그 직선을 붙여준 것이다.

이는 trivial bundle이 아니다. 만일 이것이 trivial bundle이었다면, non-vanishing continuous section $\RP^n\rightarrow E(\gamma_n^1)$이 존재했을 것이다. 가령 $B$의 모든 점에 fiber의 $1$을 대응시키는 함수가 그러하다. 그런데 임의의 section $s:\RP^n \rightarrow E(\gamma_n^1)$이 주어졌다 하고, quotient map $q:S^n \rightarrow \RP^n$을 사용한 다음의 합성

\[S^n \overset{q}{\longrightarrow} \RP^n \overset{s}{\longrightarrow} E\overset{\pr_2}{\longrightarrow} \mathbb{R}^{n+1}\]

을 생각하면 이 함수는 $\mathbf{x}\in S^n\subset\mathbb{R}^{n+1}$을 $\mathbf{x}$의 상수배로 보낸다. 이 상수를 $t(\mathbf{x})$라 하면, $t$는 $S^n$에서 $\mathbb{R}$로의 연속함수이고 quotient map $q$로 인하여

\[t(-\mathbf{x})=-t(\mathbf{x})\]

를 만족한다. 이제 $S^n$은 connected이므로 중간값정리에 의하여 $t(\mathbf{x}_0)=0$을 만족하는 $\mathbf{x}_0\in S^n$이 존재한다.

더 일반적으로 다음이 성립한다.

명제 4 위상공간 $B$ 위에 정의된 vector bundle $E$ of rank $n$에 대하여, $E$가 trivial bundle인 것은 everywhere linearly independent인 $n$개의 section들 $s_1,\ldots, s_n$이 존재하는 것과 동치이다.

한편 임의의 vector bundle $p:E \rightarrow B$와 임의의 연속함수 $f:B’\rightarrow B$가 주어졌을 때, 우리는 다음의 식

\[f^\ast E=\{(x,v)\in B'\times E\mid f(x)=p(v)\}\subset E\]

로 두어 새로운 vector bundle $f^\ast E \rightarrow B’$를 정의할 수 있다. 우리는 이를 pullback bundle이라 부르며, 어렵지 않게 임의의 vector bundle $E’ \rightarrow B’$가 위의 조건을 만족한다면 $f^\ast E$를 factor through하는 것을 알 수 있다.

한편 임의의 두 vector bundle $p_1:E_1\rightarrow B_1$, $p_2:E_2\rightarrow B_2$가 주어진다면 이들의 곱

\[p_1\times p_2: E_1\times E_2 \rightarrow B_1\times B_2\]

또한 $B_1\times B_2$ 위의 vector bundle임을 안다. 이제 만일 $B_1=B_2=B$일 경우, 언제나와 같이 diagonal map

\[\Delta: B\rightarrow B\times B\]

를 사용하면 pullback bundle $\Delta^\ast(p_1\times p_2)$는 $B$ 위의 bundle이 된다. 이를 두 vector bundle $E_1\rightarrow B$, $E_2\rightarrow B$의 Whitney sum이라 부르고 $p_1\oplus p_2:E_1\oplus E_2\rightarrow B$와 같이 표기한다. 그 표기에서 알 수 있듯이 이는 fiberwise하게는 두 vector bundle $E_1,E_2$의 fiber의 direct sum에 해당한다.

비록 자세한 증명을 하지는 않았지만, 비슷한 방식으로 우리는 각각의 fiber (즉 벡터공간)에 정의되는 연산들을 vector bundle로 옮겨올 수 있다. 가령 두 vector bundle $E_1\rightarrow B$, $E_2 \rightarrow B$에 대하여 이들의 tensor product bundle $E_1\otimes E_2 \rightarrow B$를 만들 수 있으며, $\Hom$이나 $\bigwedge$ 등의 연산을 사용하는 것도 가능하다.

체흐 코호몰로지

이쯤에서 우리는 또 다른 코호몰로지 이론을 정립한다. 이는 sheaf cohomology (§푸앵카레 쌍대성, ⁋정의 14)와 마찬가지로 위상공간 위에 정의되는 sheaf에 대한 cohomology이며, étale space construction을 통하여 stalk이 벡터공간인 sheaf와 vector bundle을 같은 것으로 생각할 수 있으므로 우리 이야기에서 중요한 역할을 한다.

Sheaf cohomology는 sheaf의 global section의 존재에 대한 obstruction을 cohomology가 담고 있다는 것을 보여줬다. 지금 살펴볼 체흐 코호몰로지도 그 결과는 비슷하지만, 이에 대한 답을 local section들을 이어붙여 global section을 만드는 과정에서 살펴본다는 점에서 차이가 있다. 어쨌든, manifold를 포함하는 좋은 경우에 체흐 코호몰로지는 sheaf cohomology와 같은 결과를 주고, 따라서 constant sheaf의 체흐 코호몰로지는 우리가 원래 알던 cohomology를 복원한다.

위상공간 $X$와 그 위에 정의된 sheaf $\mathscr{F}$, 그리고 $X$의 open cover $\mathcal{U}=\{U_i\}_{i\in I}$를 생각하자. 각각의 $p\geq 0$에 대하여, Čech $p$-cochain들의 group은 다음의 식

\[\check{C}^p(\mathcal{U},\mathscr{F})=\prod_{i_0,\ldots,i_p}\mathscr{F}(U_{i_0}\cap \cdots\cap U_{i_p})\]

으로 정의된다. 즉 이는 모든 $p$개의 intersection들 위에 정의된 section들의 모임이다. 이 때 differential

\[\check{C}^p(\mathcal{U},\mathscr{F})\rightarrow \check{C}^{p+1}(\mathcal{U}, \mathscr{F})\]

은 다음의 식

\[(\delta c)_{i_0,\ldots, i_{p+1}}=\sum_{k=0}^{p+1} (-1)^k c_{i_0,\ldots,\hat{i}_k,\ldots,i_{p+1}}\vert_{U_{i_0}\cap\cdots\cap U_{i_{p+1}}}\]

로 주어진다. 그럼 Čech cohomology는 다음의 식

\[\check{H}^p(\mathcal{U}, \mathscr{F})=\frac{\ker(\check{C}^p\rightarrow \check{C}^{p+1})}{\im(\check{C}^{p-1}\rightarrow \check{C}^{p})}\]

으로 주어진다. 만일 $\mathcal{U}$가 충분히 좋은 cover라면, 가령 임의의 finite intersection이 contractible하거나, $\mathscr{F}$에 대해 acyclic하다면 우리는 canonical isomorphism

\[H^p(X,\mathscr{F})\cong \check{H}^p(\mathcal{U},\mathscr{F})\]

을 얻는다.

이제 임의의 rank $n$ vector bundle은 그 fiber가 open cover 위에서 어떻게 붙는지에 따라 결정된다. 즉 함수들

\[g_{ij}:U_{ij}=U_i\cap U_j \rightarrow \GL(n;\mathbb{R})\]

에 의해 결정된다. 이들은 다음의 조건

\[g_{ij}\cdot g_{jk}\cdot g_{ki}=\id\]

을 만족해야 하며, 만일 이 조건이 없다면 triple intersection $U_i\cap U_j\cap U_k$에서, $U_i$의 local trivialization을 $g_{ij}$를 통해 $U_j$로, 이를 다시 $g_{jk}$를 통해 $U_k$로, 이를 다시 $g_{ki}$를 통해 $U_i$로 가져왔을 때 trivialization이 달라져 있겠지만 실제로는 그렇지 않다는 것을 의미한다. 그럼 transition function들 $g_{ij}$들은 Čech 1-cochain들이 되며, 따라서 local trivialization $U_i\rightarrow \GL(n;\mathbb{R})$을 고정하면 rank $n$ vector bundle들의 isomorphism class들과 $1$-cochain들 사이의 일대일 대응이 있는 것을 안다. 즉, open cover $U$ 위에서 trivializable한 rank $n$ vector bundle들의 isomorphism class들과 $\check{H}^1(\mathcal{U}, \GL(n;\mathbb{R}))$ 사이의 일대일 대응이 있다.

앞서 우리는 §푸앵카레 쌍대성, ⁋명제 4에서 manifold $M$의 $A$-orientability가 다음의 group homomorphism

\[\pi_1(M,x)\rightarrow A^\times\]

에 의해 정의되는 것을 보았다. 한편 $A$는 commutative ring이므로, 위의 group homomorphism은 다음의 abelian group homomorphism

\[H_1(M)\rightarrow A^\times\]

으로 factor through하고 이는 §코호몰로지, ⁋명제 3에 의하여 $H^1(M;A)$의 원소이다. 만일 이 원소가 $0$이라면 monodromy action이 trivial action이라는 것과 같고, 이는 곧 $\Spe(\or_M^A)$이 trivial covering space라는 뜻이 되어 $M$이 $A$-orientable manifold가 되었다. 한편 임의의 commutative ring $A$에 대하여, $\cRing$의 initial object가 $\mathbb{Z}$이므로 임의의 manifold $M$에 대하여 $\mathbb{Z}$-orientation $H_1(M)\rightarrow \mathbb{Z}^\times$가 결정되면 이를 $\mathbb{Z}^\times\rightarrow A^\times$와 합성하여 $A$-orientation $H_1(M)\rightarrow A^\times$를 결정할 수 있으므로, $\Spe(\or_M^A)$가 trivial cover인지에 대한 본질적인 정보는 $H^1(M;\mathbb{Z}/2)$에 들어있는 것을 알고 있으며, $\mathbb{Z}/2$를 $\GL(1;\mathbb{Z})$로 생각하면 이것은 first cohomology가 어떻게 covering space에 대한 정보를 담고있는지에 대한 예시이다.

이러한 방식으로, vector bundle $E\rightarrow B$ of rank $k$에 대한 정보는 $\check{H}^1(B; \underline{\GL(k,\mathbb{R})})$에 담겨있다고 볼 수 있다. 그러나 우리가 사용하는 $B$의 cohomology의 coefficient는 $\mathbb{Z}$이기 때문에 여기에 담겨있는 모든 데이터를 갖고있지는 않다. 대신 우리는 이를 약하게 대체할만한 대상, 즉 invariant들을 cohomology ring $H^\bullet(B)$에서 찾는 것이 목표이다.

슈티펠-휘트니 특성류

첫 번째로 살펴볼 characteristic class는 Stiefel-Whitney class이다. 우선 이는 임의의 vector bundle $p:E\rightarrow B$가 주어질 때마다 정의되는 cohomology ring $H^\bullet(B;\mathbb{Z}/2)$의 원소 $w(p)$이며, 위와 마찬가지로 만일 $w(p)=0$이라면 $E$는 trivial bundle이 된다. 즉 만일 $w(p)=0$이라면, 명제 4에 의하여, $n=\rank(E)$개의 everywhere linearly independent continuous section이 존재한다. 뿐만 아니라 $w(p)$를 cohomology ring의 degree에 맞춰

\[w(p)=w_0(p)+w_1(p)+\cdots\]

으로 분해하면, 각각의 $w_i(p)$들은 $n-i+1$개의 everywhere linearly independent section들을 고르는 것에 대한 obstruction class가 된다. 즉 만일 $w_i(p)\neq 0$이라면 $n-i+1$개의 everywhere linearly independent section이 존재할 수 없다. 특히 $w_n(p)\neq 0$이라면 $1$개의 everywhere linearly independent section조차도 존재할 수 없으므로 임의의 section은 반드시 어딘가에서 $0$이 되어야 한다.

편의상 projection map $p$와 base $B$가 명확할 경우 우리는 $w(p)$ 대신 $w(E)$와 같은 표기를 사용하기도 한다. 이제 우리는 $w(E)$가 만족하는 공리들을 제시한다.

정의 5 Vector bundle $E \rightarrow B$ of rank $n$과 vector bundle $F\rightarrow B$에 대하여, 다음의 공리를 만족하는 cohomology class $w_i(E)\in H^i(B;\mathbb{Z}/2)$를 Stiefel-Whitney class_{슈티펠-휘트니 특성류}라 부른다.

1. (Rank) $w_0(E)=1$이며, 만일 $i>n$이라면 $w_i(E)=0$이다.
2. (Naturality) 임의의 $f:B’\rightarrow B$에 대하여, $w(f^\ast E)=f^\ast w(E)$가 성립한다.
3. (Whitney product formula) $w(E\oplus F)=w(E)w(F)$가 성립한다.
4. (Normalization) 예시 3의 tautological line bundle $\gamma_1^1:E(\gamma_1^1)\rightarrow \RP^1$에 대하여, $w_1(\gamma_1^1)\neq 0$이다.

그럼 다음 결과들이 자명하다.

명제 6 두 vector bundle $p_1:E_1\rightarrow B_1$, $p_2:E_2\rightarrow B_2$에 대하여, 만일 $p_1,p_2$이 isomorphic하다면 $w(E_1)=w(E_2)$이다. 특히, 만일 $p:E\rightarrow B$가 trivial bundle이라면 $w(E)=0$이다.

첫째 주장은 자명하다. 둘째 주장의 경우, trivial bundle은 다음의 pullback

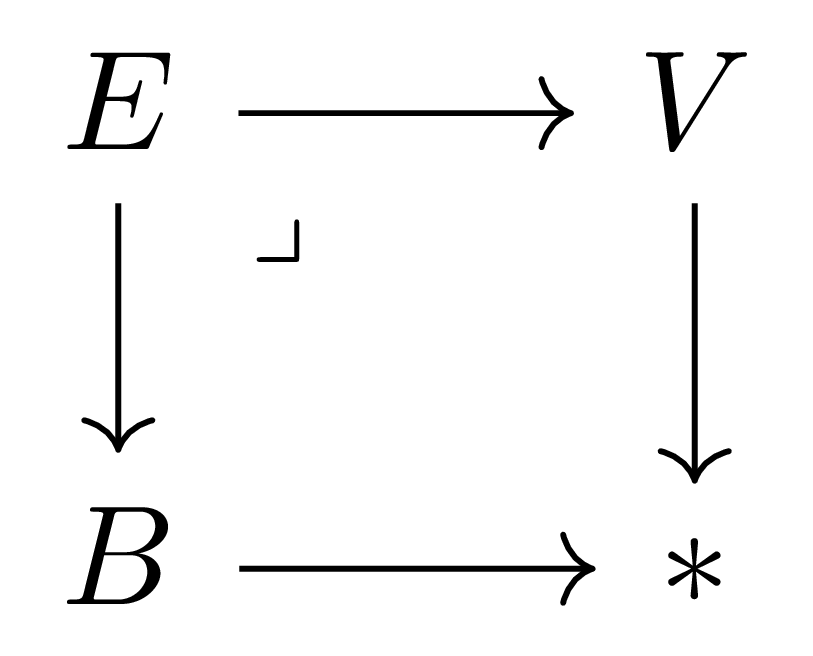
으로 주어지는 것을 확인하면 된다.

흥미로운 관찰은 $S^1$의 line bundle의 isomorphism class는 오직 두 가지, 즉 trivial line bundle과 예시 3의 line bundle 뿐이라는 것이며, 실제로 $S^1$ 위에 정의된 line bundle 중, “두 번 꼬아” 얻어지는 line bundle은 trivial line bundle과 isomorphic하다는 것을 확인할 수 있다. 이는 명제 6을 보면 어느정도 예측가능한 것으로, $S^1$ 위의 line bundle의 Stiefel-Whitney class는 $H^1(S^1;\mathbb{Z}/2)$에 존재해야 하며 이는 $\mathbb{Z}/2$와 isomorphic하기 때문이다.

이들은 $\RP^1$의 tautological line bundle의 pullback이라는 것이다. $S^1$의 trivial line bundle의 경우, $S^1$의 모든 점을 $\RP^1$의 고정된 점으로 보내는 연속함수로의 pullback이며 nontrivial한 line bundle은 quotient map $S^1 \rightarrow \RP^1$을 통한 line bundle의 pullback이다.

그라스만 다양체

더 일반적으로, 임의의 공간 위의 rank $k$ vector bundle은 infinite Grassmannian $\Gr_k(\mathbb{R}^\infty)$의 universal bundle $\gamma^k_\infty:E(\gamma_\infty^k)\rightarrow \Gr_k(\mathbb{R}^\infty)$을 pullback하여 얻어진다. 즉 임의의 vector bundle $p:E \rightarrow B$가 주어졌다면, $p$에서 $\gamma_k^\infty$로의 유일한 bundle map이 존재하여 다음의 diagram

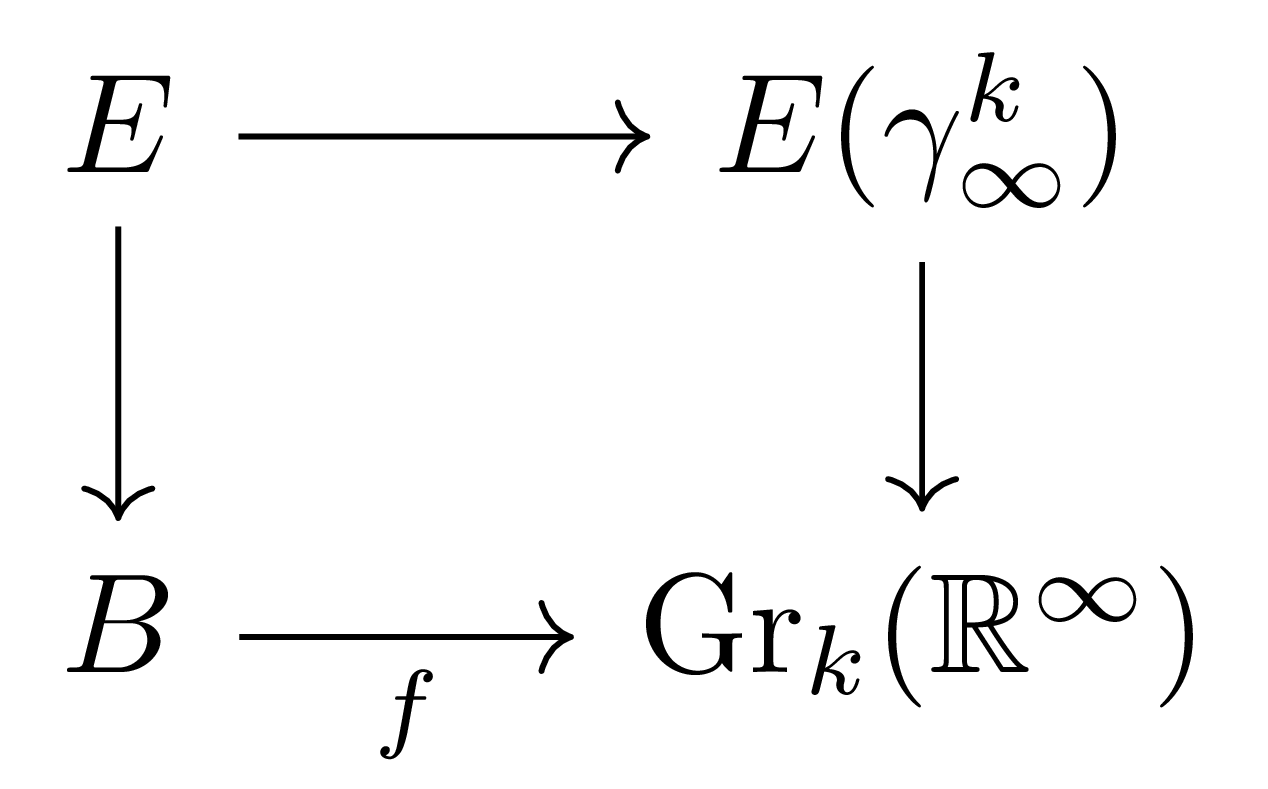
을 commute하도록 할 수 있고, 이는 다음의 pullback diagram

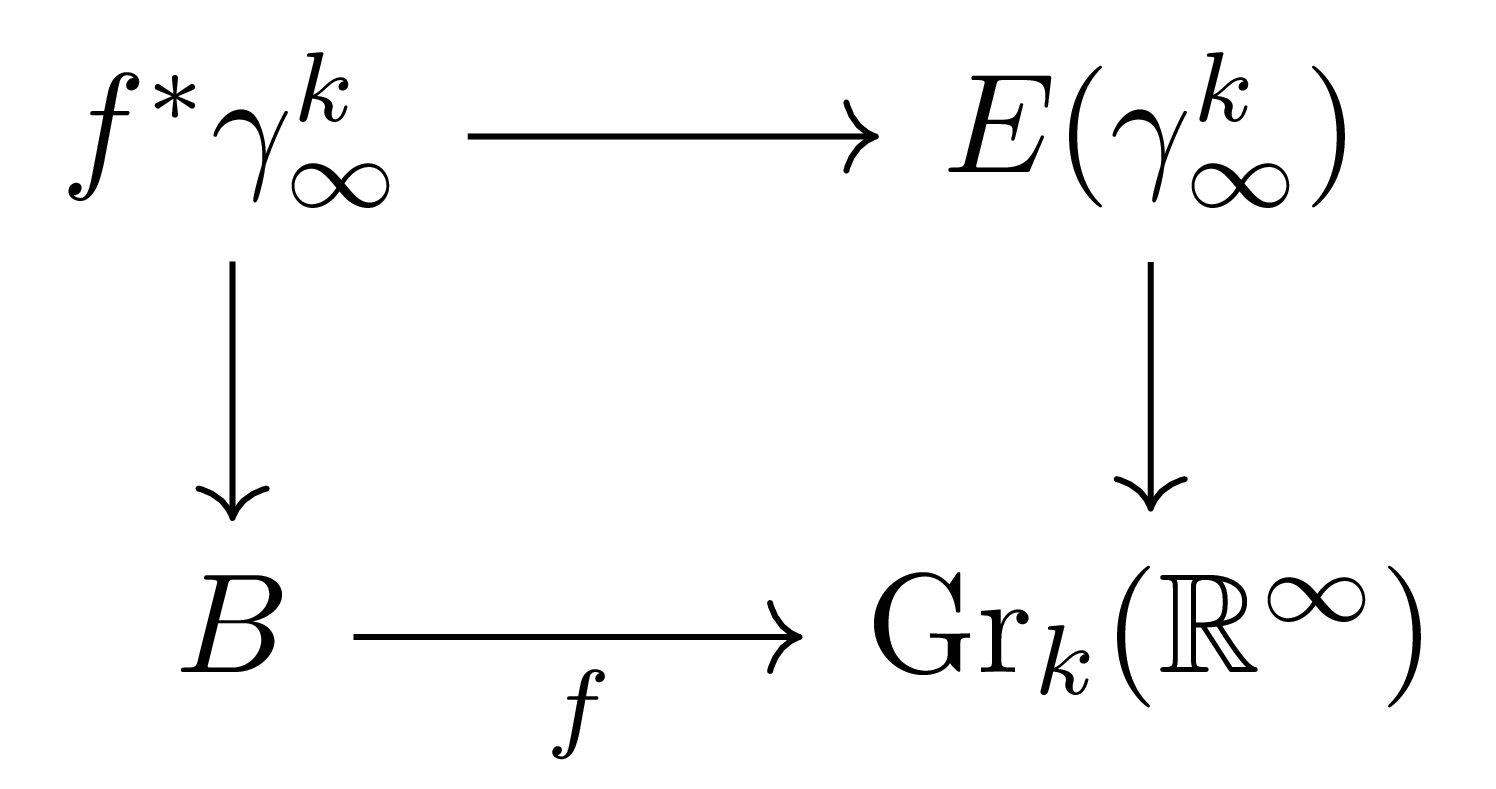
과 isomorphic하다. 뿐만 아니라, vector bundle $E$의 Stiefel-Whitney class 또한 universal bundle $\gamma^k_\infty$의 Stiefel-Whitney class $w(\gamma^k_\infty)$를 pullback하여 얻어진다.

따라서 우리는 (infinite) Grassmannian과 그 위의 universal bundle, 그리고 이 bundle의 Stiefel-Whitney class가 존재하는 infinite Grassmannian의 cohomology ring $H^\bullet(\Gr_k(\mathbb{R}^\infty), \mathbb{Z}/2)$에 대해 살펴보아야 한다. Grassmannian의 성질을 모두 엄밀하게 증명하는 것은 복잡한 일이므로, 이 절에서는 이들 성질에 대한 소개와, (가능하다면) 간단한 설명을 주는 것으로 만족하기로 한다.

우선 우리는 $\Gr_k(\mathbb{R}^n)$의 기본적인 성질들과 cohomology ring을 살펴본다. 정의에 의해 $\Gr_k(\mathbb{R}^{n})$은 $\mathbb{R}^{n}$의 모든 $k$차원 linear subspace들의 공간이다. 예를 들어 $\Gr_1(\mathbb{R}^{n+1})$은 그 정의에 의하여 projective space $\RP^n$이다. $\Gr_k(\mathbb{R}^{n})$의 각각의 점들은 $\mathbb{R}^{n}$의 부분공간이므로, 우리는 두 점 (즉 $\mathbb{R}^{n}$의 두 $k$차원 부분공간)이 서로 얼마나 가까운지를 직관적으로 알고 있다. 이는 가령, $\mathbb{R}^{n+1}$에서 “기울기”가 비슷한 두 직선에 해당하는 점들이 $\RP^n$에서 가까운 점들인 것과 동일한 일이며, 이는 $n\times k$행렬을 이용하여 엄밀하게 정의할 수 있으며, 이 위상구조 하에서 $\Gr_k(\mathbb{R}^{n})$은 $k(n-k)$차원 compact topological manifold가 된다.

이제 이들의 cohomology ring을 살펴보자. 우리는 어차피 $\mathbb{Z}/2$-coefficient를 사용하고 있으므로, §푸앵카레 쌍대성, ⁋정리 11에 의하여, $\Gr_k(\mathbb{R}^n)$의 homology cycle을 생각해도 된다.

이를 위해 $\mathbb{R}^n$의 full flag

\[F_\bullet:\qquad 0=F_0\subset F_1\subset F_2\subset\cdots\subset F_n=\mathbb{R}^n\]

을 고정하자. 그럼 $\mathbb{R}^n$에 속한 임의의 $k$-plane $X$는

\[0=\dim (X\cap F_0)\leq\dim(X\cap F_1)\leq\cdots\leq \dim(X\cap F_n)=k\]

을 정의하며, 이 수열은 $X$가 $\mathbb{R}^n$ 안에 어떻게 들어있는지를 보여준다. 이를 추적하기 위해 우리는 Schubert symbol $\sigma=(\sigma_1,\ldots, \sigma_k)$을 다음 조건

\[1\leq \sigma_1<\sigma_2<\cdots<\sigma_k\leq n\]

을 만족하는 수열로 정의한다. 이들 $\sigma_i$들은 공간 $X\cap F_i$이 언제 커지는지를 보여준다. 즉 이들은

\[\dim(X\cap F_{\sigma(i)})=i, \qquad \dim(X\cap F_{\sigma(i)-1})=i-1\]

을 통해 차원이 뛰는 곳을 측정하는 정보를 담을 수 있다. 이를 거꾸로 뒤집으면 우리는 적당한 partition

\[\lambda:\qquad \lambda_1\geq\lambda_2\geq\cdots\geq\lambda_k,\qquad \lambda_1\leq n-k\]

에 다음의 조건

\[\dim(X\cap F_{n-k+i-\lambda_i})\geq i\]

을 부여하여 이 정보를 담을 수 있다. 이들 partition은, flag

\[F_0\subset F_1\subset\cdots\subset F_n\]

를 고정했을 때 $X\cap F_i$의 차원이 언제 뛰었는지를 보여준다. 예를 들어 $X=F_k$일 때 이에 해당하는 partition은 $(0,0,\ldots,0)$이며, 이는 $X\cap F_i$들이 딜레이 없이, $i$가 증가함에 따라 처음 $k$개의 항에서 모든 차원의 점프가 완료된다는 뜻이다. 가령 $(0,1,0,\ldots,0)$은, $X\cap F_1$은 1차원, $X\cap F_2$도 $1$차원, $X\cap F_3$은 2차원이며 그 후로는 차원이 하나씩 딜레이 없이 뛴다는 것이다.

이제 이를 바탕으로 다음의 부분집합

\[\Omega_\lambda^\circ(F_\bullet)=\left\{V\in\Gr_k(F_n)\mid\text{$\dim(V\cap F_{n-k+i-\lambda_i})= i$ for all $1\leq i\leq k$}\right\}\]

을 생각하면, 이들은 각각 그 closure

\[\Omega_\lambda(F_\bullet)=\left\{V\in\Gr_k(F_n)\mid\text{$\dim(V\cap F_{n-k+i-\lambda_i})\geq i$ for all $1\leq i\leq k$}\right\}\]

안에서 open submanifold이며, 이들 $\Omega_\lambda(F_\bullet)$들은 inclusion

\[\Omega_\lambda(F_\bullet)\hookrightarrow \Gr_k(\mathbb{R}^n)\]

을 통하여 $\Gr_k(\mathbb{R}^n;\mathbb{Z}/2)$의 homology class를 정의한다. 우리는 이들을 Schubert cycle이라 부르고, 이들의 Poincaré dual $\sigma_\lambda$을 Schubert class라 부른다. 이들은 degree $\lvert \lambda\rvert=\sum \lambda_i$의 cohomology class들이다. 이 때, 각각의 부분공간 $\Omega_\lambda(F_\bullet)$들은 flag $F_\bullet$의 선택에 의존하지만, 이들의 homology에서의 image인 Schubert cycle들은 $F_\bullet$의 선택에 의존하지 않고 따라서 Schubert class들도 그러하다. 또, $H^\bullet(\Gr_k(\mathbb{R}^n);\mathbb{Z}/2)$은 앞선 조건을 만족하는 partition $\lambda$들로 생성되는 polynomial algebra들이며, 따라서 우리는 이들 사이의 cup product 구조만 보면 충분하다.

예시 7 예를 들어 $\Gr_2(\mathbb{R}^4;\mathbb{Z}/2)$를 보자. 우리는 여기에서 partition $(1,0)$에 해당하는 Schubert class $\sigma_{(1,0)}$의 제곱

\[\sigma_{(1,0)}\smile\sigma_{(1,0)}=\sigma_{(1,1)}+\sigma_{(2,0)}\]

에 대해 살펴볼 것이다. 우리의 기하학적 직관을 활용하기 위해 §푸앵카레 쌍대성, ⁋예시 15에서와 같이 이를 Schubert cycle들의 intersection으로 생각하자. 우리는 이를 위해 $\sigma_{(1,0)}$에 해당하는 homology class 중, general position에 있는 두 부분공간을 생각해야 하며 이는 flag의 선택을 바꾸어줌으로서 가능하다.

고정된 flag $F_\bullet$에 대해, partition $\lambda=(1,0)$이 나타내는 조건이 무엇인지를 명시적으로 나타내면 이는 다음의 조건

\[\dim(X\cap F_{4-2+1-1})=\dim(X\cap F_2)\geq 1,\qquad \dim(X\cap F_{4-2+2-0})=\dim (X\cap F_4)\geq 2\]

이다. 즉 실질적으로 유효한 조건은 $\dim(X\cap F_2)\geq 1$ 뿐이다. 즉, $X$가 $F_2$를 1차원 이상에서 만난다는 뜻이며, 이는 $F_2$에 포함된 적당한 직선 $L$을 이용하여, $X$가 이 직선 $L$을 포함한다는 조건으로 바꾸어 쓸 수 있다.

이제 cup product $\sigma_{(1,0)}\smile\sigma_{(1,0)}$을 계산하기 위해서는 general position에 있는 두 flag $F_\bullet$과 $F_\bullet’$을 생각해야 한다. 가령

\[F_\bullet:\quad \langle e_1\rangle\subset \langle e_1,e_2\rangle\subset \langle e_1,e_2,e_3\rangle,\qquad F_\bullet':\quad \langle e_4\rangle\subset \langle e_3,e_4\rangle\subset \langle e_2,e_3,e_4\rangle\]

이 그러하다. 이제 우리가 고려할 $V$들은 $\langle e_1,e_2\rangle$과도, $\langle e_3,e_4\rangle$과도 $1$차원으로 만나야 한다. 이를 위해 또 다른 flag

\[G_\bullet:\quad \langle e_1+e_4\rangle\subset\langle e_1+e_4,e_2+e_3\rangle\subset \langle e_1+e_4,e_2+e_3,e_2-e_3\rangle\]

을 생각하자. 그럼 두 가지의 경우가 있는데, 우선 하나의 경우는 $F_2,F_2’$의 두 line으로 만들어지는 평면이 $G_3$에 포함되어있지 않은 경우이다. 예를 들어 $V$와 $F_2$가 $\span(e_1+e_2)$에서 만나고, $V$와 $F_2’$가 $\span(e_3+e_4)$에서 만나는 경우가 이에 해당한다. 이 경우, $V$는 정확하게 $\span(e_1+e_2,e_3+e_4)$로 쓰여질 수 있으며, 이는 $G_0,G_1$와는 $0$차원, $G_2,G_3$과는 $1$차원, 그리고 $G_4$에서야 $2$차원으로 만난다. 즉 이는 $(1,1)$에 해당하는 경우이다.

다른 하나의 경우는 $F_2,F_2’$의 두 line으로 만들어지는 평면이 $G_3$에 포함되는 경우이다. 가령 $V$와 $F_2$가 $\span(e_2)$에서 만나고, $V$와 $F_3$이 $\span(e_3)$에서 만나는 경우를 생각하면 $V=\span(e_2,e_3)$이며 이는 $G_3$에 포함된다. 이 경우는 $(2,0)$에 해당된다.

더 일반적으로 우리는 이들 partition을 Young diagram으로 나타내고, 이를 이용하여 두 Schubert class의 cup product $\sigma_\lambda\smile\sigma_\mu$를 계산했을 때, $\lvert\nu\rvert=\lvert\lambda\rvert+\lvert\mu\rvert$를 만족하는 $\nu$에 대해 $\sigma_\nu$ 앞에 붙는 계수를 계산할 수 있다.

이제 우리는 $\Gr_k(\mathbb{R}^\infty)$와 그 위의 universal bundle을 정의해야 한다. 이를 위해 $\Gr_k(\mathbb{R}^n)$ 위의 tautoogical bundle을 먼저 정의한다. 예시 3과 같은 방식으로, $\Gr_k(\mathbb{R}^{n+k})$의 각각의 점마다 그 점에 해당하는 vector space를 달아주는 다음의 bundle

\[E(\gamma^k_n)=\left\{([V], x)\in \Gr_k(\mathbb{R}^{n+k})\mid \text{$V$ a $k$-dimensional subspace of $\mathbb{R}^{n+k}$ and $x\in V$}\right\}\]

이 존재하며 이를 $\Gr_k(\mathbb{R}^{n+k})$의 tautological bundle이라 부른다.

이제 각각의 $n$에 대하여, 다음의 식

\[\mathbb{R}^{k+n} \rightarrow \mathbb{R}^{k+n+1};\qquad (x_1,\ldots,x_{k+n}) \mapsto (x_1,\ldots,x_{k+n},0)\]

은 $\mathbb{R}^{k+n}$의 $\mathbb{R}^{k+n+1}$로의 inclusion을 정의하며, 우리는 이를 통해 $\mathbb{R}^{k+n}$의 $k$차원 subspace를 $\mathbb{R}^{k+n+1}$의 $k$차원 subspace로 볼 수 있다. 즉 위의 inclusion은 Grassmannian 사이의 inclusion $\Gr_k(\mathbb{R}^{k+n})\rightarrow \Gr_k(\mathbb{R}^{k+n+1})$을 유도한다. 이제 다음의 directed system

\[\Gr_k(\mathbb{R}^k)\hookrightarrow \Gr_k(\mathbb{R}^{k+1})\hookrightarrow\cdots\]

을 생각하면, 우리는 이들의 direct limit

\[\Gr_k(\mathbb{R}^\infty)=\varinjlim_{n\geq 0}\Gr_k(\mathbb{R}^{k+i})\]

을 infinite Grassmannian이라 부른다. 마찬가지 방식으로 total space들의 direct limit

\[E(\gamma_\infty^k)=\varinjlim_{n\geq 0} E(\gamma^k_{k+n})\]

이 정의되며 이것이 $\Gr_k(\mathbb{R}^\infty)$ 위의 rank $k$ vector bundle을 정의한다. 이들은 당연히 inclusion $\mathbb{R}^{k+n}\hookrightarrow \mathbb{R}^{k+n+1}$의 선택에 의존하지 않는다.

직관적으로 $\Gr_k(\mathbb{R}^\infty)$는 각각의 $\Gr_k(\mathbb{R}^{k+n})$들을 이어붙여 complex 구조를 주는 것으로 생각할 수 있다. 뿐만 아니라 tautological bundle들 $E(\gamma^k_{n+k})$들도 이 구조와 호환되도록 붙어있게 된다.

Finite Grassmannian의 Schubert class들을 infinite Grassmannian으로 옮기는 것은 방향이 맞지 않다. 그러나, 위에서 설명했듯 infinite Grassmannian은 finite Grassmannian들을 subcomplex로 가지는 공간이며, 위에서 만든 Schubert cycle들은 이 inclusion들에 대해 잘 행동한다. 즉 partition $\lambda$에 해당하는 $\Gr_k(\mathbb{R}^{k+i})$의 Schubert cycle을 $\Gr_k(\mathbb{R}^{k+i})\rightarrow \Gr_k(\mathbb{R}^{k+i+1})$를 통해 집어넣은 것이나, $\Gr_k(\mathbb{R}^{k+i+1})$에서 바로 partition $\lambda$에 해당하는 Schubert cycle을 $\Gr_k(\mathbb{R}^n)\subset \Gr_k(\mathbb{R}^{k+i+1})$과 교집합한 것이나 같은 결과를 준다.

이제 $k$개의 partition들

\[\lambda_1=(1,0,\cdots, 0),\quad \lambda_2=(2,0,\cdots,0),\qquad \lambda_k=(k,0,\cdots,0)\]

을 생각하자. 그럼 이들은 위의 논증에 의하여 $\Gr_k(\mathbb{R}^\infty)$의 homology class들이 되어 다음의 함수

\[w_i: H_\bullet(\Gr_k(\mathbb{R}^\infty);\mathbb{Z}/2)\rightarrow \mathbb{Z}/2; \qquad \text{$w_i(\Omega_{\lambda_i}(F_\bullet))=1$ and is $0$ otherwise}\]

들이 $i$번째 cohomology class $H^i(\Gr_k(\mathbb{R}^\infty);\mathbb{Z}/2)$에 있으며, 따라서 우리는

\[w_1\in H^1(\Gr_k(\mathbb{R}^\infty);\mathbb{Z}/2),\cdots, w_k\in H^k(\Gr_k(\mathbb{R}^\infty);\mathbb{Z}/2)\]

임을 안다. 그럼 $H^\bullet(\Gr_k(\mathbb{R}^\infty);\mathbb{Z}/2)$는 polynomial algebra로서 이들 $w_i$에 의해 생성된다. 가령, 임의의 partition $(a_1,\cdots,a_n)$은 다음 monomial

\[w_1^{a_1}w_2^{a_2}\cdots w_k^{a_k}\]

에 대응되며 이는 $H^\bullet(\Gr_k(\mathbb{R}^\infty);\mathbb{Z}/2)$의 (무한히 많은) $\mathbb{Z}/2$-module로서의 gemerator 중 하나가 되며 이는 앞에서 언급한 Littlewood-Richardson rule에 의해 계산된다. 이제 이들 $w_i$들은 Stiefel-Whitney class가 만족하는 공리들을 모두 만족하며, 이것이 pullback에 의해 보존되는 것으로부터 존재성이 증명된다.

오일러 특성류

지금까지 우리는 $\mathbb{Z}/2$-coefficient를 사용하여 orientability의 문제를 효과적으로 피해왔다. 이제 우리는 orientation까지 고려하기로 한다.