호모토피

위상적 불변량들

일반적으로 우리는 수학적 대상들이 주어졌을 때 이들 대상을 (isomorphism에 대하여) 분류하는 것에 관심이 있다. 가령 집합들은 그 크기로 완전히 분류되고, \(\mathbb{k}\)-벡터공간들은 그 차원으로 완전히 분류된다. 그러나 대부분의 경우 이러한 classification은 쉬운 일이 아니며, 위상공간 또한 그러하다.

우리가 앞선 글에서 정의한 위상공간의 호몰로지들은 functoriality에 의하여 위상적인 불변량들이다. 즉, 만일 두 위상공간 \(X\)와 \(Y\)가 homeomorphic하다면 이들은 homologous하기도 하다. 그러나 일반적으로 그 역은 성립하지 않는다. 그렇다면 위상공간을 완전히 결정하는 위상적 불변량을 찾는 것이 우리의 희망 중 하나가 될 것이지만, 다음의 재미있는 결과가 있다.

정리 1 (Markov 1958) 4차원 이상의 두 topological manifold가 서로 homeomorphic한지 알려주는 유한한 알고리즘은 존재하지 않는다.

나이브하게 바꿔 말하면, 만일 임의의 위상공간이 서로 homeomorphic한지를 알려주는 위상적인 불변량이 존재한다면 이 불변량을 계산하는 적절한 방법은 일반적으로 존재하지 않는다. 이러한 관점에서 보자면, 위상적인 불변량들은 어떠한 두 위상공간이 homeomorphic하다는 것을 증명할 때 사용하는 것이 아니라, 어떠한 두 위상공간이 homeomorphic하지 않다는 것을 보일 때만 유용하다고도 말할 수 있다.

호모토피 동형

이번 글에서 소개할 호모토피 동형은, 마찬가지로 어떠한 두 위상공간이 homeomorphic하지 않음을 보일 때 유용하며, 뿐만 아니라 호몰로지가 정의하는 equivalence보다 더 섬세하기도 하다. 즉, 다음의 함의관계

\(X,Y\text{ homeomorphic}\implies X,Y \text{ homotopically equivalent}\implies X,Y\text{ homologous}\tag{\)\ast\(}\)

가 성립하지만 그 역은 성립하지 않는다. 뿐만 아니라 호모토피 동형은 호몰로지에 비하여 조금 더 기하학적으로 직관적이기도 하다.

정의 2 두 위상공간 \(X,Y\) 사이의 연속함수들 \(f_0,f_1:X \rightarrow Y\)이 주어졌다 하자. 그럼 \(f_0\)와 \(f_1\)이 homotopic_호모토픽하다는 것은 연속함수 \(F:X\times [0,1]\rightarrow Y\)가 존재하여 다음 두 식

\[F(x,0)=f_0(x),\qquad F(x,1)=f_1(x)\tag{1}\]

이 모든 \(x\in X\)에 대해 성립하는 것이다. 이 경우, \(F\)를 \(f_0\)과 \(f_1\) 사이의 homotopy_호모토피라 부르고, \(f_0\)과 \(f_1\) 사이의 homotopy가 존재하면 이를 \(f_0\simeq f_1\)로 적는다.

직관적으로 이는 \(f_0\)을 연속적으로 변형하여 \(f_1\)을 얻을 수 있다는 의미를 갖는다. 위의 정의에서, 연속함수 \(F\)가 주어지는 것은 연속함수들의 family \((F(-,t))_{t\in[0,1]}\)가 주어지는 것과 같다. 이러한 관점에서 \(f_0\)과 \(f_1\) 사이의 homotopy \(F\)를 \((f_t)_{t\in[0,1]}\)와 같이 적기도 한다.

명제 3 관계 \(\simeq\)는 \(C(X,Y)\) 위의 동치관계이다.

증명

1. 우선 \(\simeq\)는 reflexive하다. 이는 임의의 \(f\in C(X,Y)\)에 대하여, \(F(x,t)=f(x)\)로 정의하면 이것이 \(f\)와 자기 자신 사이의 homotopy를 정의하기 때문이다.

2. 그리고 \(\simeq\)는 symmetric하다. \(f_0\simeq f_1\)이라 가정하면, 식 (1)을 만족하는 homotopy \(F\)가 존재한다. 이제 \(\tilde{F}(x,t)=F(x,1-t)\)로 정의하면 \(\tilde{F}\)는 연속함수이며 두 식

   \[\tilde{F}(x,0)=f_1(x),\qquad\tilde{F}(x,1)=f_0(x)\]

   을 만족한다. 따라서 \(f_1\simeq f_0\)이 성립한다.

3. 마지막으로 \(\simeq\)는 transitive하다. \(f_0,f_1,f_2\in C(X,Y)\)가 \(f_0\simeq f_1\), \(f_1\simeq f_2\)를 만족한다 하자. 그럼 두 homotopy \(F_0(x,t)\)와 \(F_1(x,t)\)가 각각 존재하여 \(F_0(x,0) = f_0(x)\)이고 \(F_0(x,1) = f_1(x)\), \(F_1(x,0) = f_1(x)\)이고 \(F_1(x,1) = f_2(x)\)를 만족한다. 이제 \(F(x,t)\)를 다음의 식

   \[F(x,t) = \begin{cases} F_0(x,2t) & \text{if } 0 \leq t \leq \frac{1}{2} \\ F_1(x,2t-1) & \text{if } \frac{1}{2} \leq t \leq 1 \end{cases}\]

   으로 정의하면, \(F\)가 \(f_0\)과 \(f_2\) 사이의 homotopy가 된다.

기본적으로 homotopic이라는 동치관계는 위와 같이 함수들에 대한 것이다. 허나 이를 사융하면 다음과 같이 두 위상공간이 호모토피 동형이라는 것이 어떤 것인지를 정의해줄 수 있다.

정의 4 두 위상공간 \(X,Y\)가 homotopically equivalent_{호모토피 동형}이라는 것은 두 연속함수 \(f:X\rightarrow Y\), \(g:Y\rightarrow X\)가 존재하여 \(f\circ g\simeq \id_Y\)이고 \(g\circ f\simeq\id_X\)인 것이다.

이 때, 위의 조건을 만족하는 두 함수 \(f,g\)를 각각 homotopy equivalence_{호모토피 동형사상}이라 부른다.

예시 5 임의의 자연수 \(n\)에 대하여, 유클리드 공간 \(\mathbb{R}^n\)은 one-point space \(\{\ast\}\)와 homotopically equivalent하다. Homotopy equivalence는

\[f:\mathbb{R}^n \rightarrow \{\ast\};\quad x\mapsto \ast,\qquad g:\{\ast\}\rightarrow \mathbb{R}^n;\quad \ast\mapsto 0\]

으로 주어진다. 그럼 \(f\circ g=\id_{\{\ast\}}\)인 것은 자명하고, \(g\circ f\simeq \id_{\mathbb{R}^n}\)의 경우는 변수 \(t\in[0,1]\)에 대하여 연속함수 \(t\cdot\id_{\mathbb{R}^n}\)를 다음의 식

\[t\cdot\id_{\mathbb{R}^n}:\mathbb{R}^n\rightarrow \mathbb{R}^n;\qquad \mathbf{x}\mapsto t\mathbf{x}\]

로 정의하면 된다.

완결성을 위해 우리는 함의관계 (\(\ast\))를 보여야 할 것이다. 이는 더 일반적인 다음의 명제에 의해 얻어진다.

명제 6 연속함수 \(f_0,f_1:X\rightarrow Y\)에 대하여, 만일 \(f_0,f_1\)가 homotopically equivalent라면 \(C_\bullet(f_0), C_\bullet(f_1)\)는 chain homotopic하다. ([호몰로지 대수학] §호몰로지, ⁋정의 5)

증명

즉, 정의에 의해 다음의 식

\[C_n(f_1)-C_n(f_0)=\partial_{n+1}^Y h_n+h_{n-1}\partial_n^X\tag{1}\]

를 만족하는 \(h_n:C_n(X) \rightarrow C_{n+1}(Y)\)을 만들어야 하며, 현재 우리가 가지고 있는 정보는 연속함수

\[F:X\times I \rightarrow Y\]

이고 정의에 의하여 \(C_n\)의 원소는 \(\Delta^n\)에서 \(X\)로의 연속함수이므로 다음의 합성

\[F\circ(\sigma\times\id_I):\Delta^n\times I \rightarrow Y\]

이 잘 정의된다. 우리는 우선 이것을 이용하여 \(C_{n+1}(Y)\)에 속하는 원소를 만들어야 한다. 이 연속함수의 정의역 \(\Delta^n\times I\)는 \((n+1)\)-simplex가 아니므로 이 대응 자체는 \(C_{n+1}(Y)\)에 속하지 않는다. 대신 우리는 이를 \((n+1)\)-simplex들의 합으로 쪼개어 이를 통해 chain homotopy를 정의할 것이다.

정의역 \(\Delta^n\times I\)의 밑면 쪽(\(t=0\)) 꼭짓점들을 \(v_0,\ldots, v_n\)이라 하고 윗면 쪽(\(t=1\)) 꼭짓점들을 \(w_0,\ldots,w_n\)이라 하자. \(n=2\)인 경우가 아래 그림에 그려져 있다.

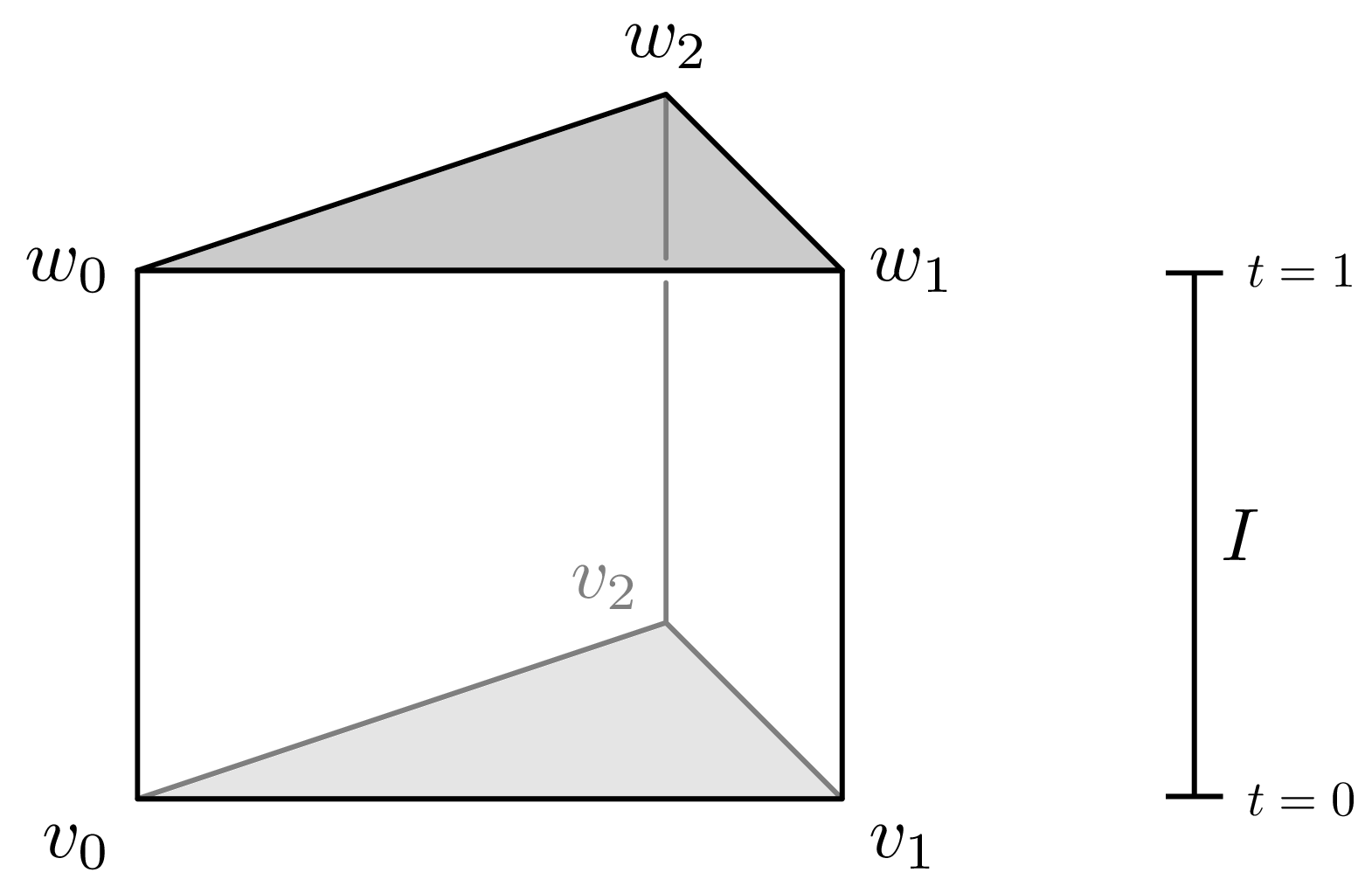
그럼 우리는 이들을 \((n+1)\)개의 \((n+1)\)-simplex들

\[[v_0,\ldots, v_n,w_n],\quad [v_0,\ldots, v_{n-1}, w_{n-1}, w_n],\quad\ldots,[v_0,w_0,\ldots, w_n]\]

으로 나눌 수 있고 마찬가지로 \(n=2\)인 경우를 그리면 다음과 같다.

이 분해를 이용하여 다음의 식

\[h_n(\sigma)=\sum_i (-1)^iF\circ(\sigma\times\id_I)\vert_{[v_0,\ldots, v_i, w_i,\ldots, w_n]}\]

으로 정의할 수 있고, 이것이 식 (1)을 만족한다는 것은 단순한 계산의 결과이다.

따라서 homotopic한 연속함수들은 homology 상에서 같은 함수를 유도한다. ([호몰로지 대수학] §호몰로지, ⁋명제 6) 특히 만일 두 공간 \(X,Y\)가 homotopically equivalent이고 \(f:X \rightarrow Y\)와 \(g:Y\rightarrow X\)가 정의 4와 같이 주어졌다면 두 공간의 homology \(H_\bullet(X)\)와 \(H_\bullet(Y)\)가 같다.

한편, 우리는 §호몰로지, ⁋예시 8의 계산으로부터 임의의 공간 \(Y\)에 대하여, 한 점 \(y\in Y\)에 해당하는 singular \(k\)-complex (\(k>0\))는 항상 \(H_k(Y)\)에서 \(0\)임을 보았다. 따라서 만일 어떠한 연속함수 \(f:X \rightarrow Y\)가 constant function과 homotopic할 경우 \(H_k(f)\)는 임의의 \(k>0\)에 대하여 zero map임을 안다. 이러한 이유로 constant function과 homotopic한 연속함수를 null-homotopic_{영호모토픽}이라 부른다. 특별히 항등함수 \(\id_X:X \rightarrow X\)가 null-homotopic일 경우 \(X\)가 contractible이라 부른다. 그럼 §호몰로지, ⁋명제 11과 위의 명제 6에 의하여 contractible space의 \(k>0\)번째 호몰로지는 항상 \(0\)임을 안다.

이제 남은 글에서 우리는 homotopy equivalence와 fundamental group에 대해 살펴본다.

Deformation retract

많은 경우 homotopically equivalent한 두 공간은 deformation retract라 부르는 변형의 결과로 나타나며, 뿐만 아니라 이들은 (다소 뜬금없이 던져진 정의 2에 비하여) 어느정도 기하학적으로 연관관계도 있다. 이를 정의하기 위해서는 우선 retraction을 정의해야 한다. ([집합론], §Retraction과 section, ⁋정의 2)

정의 7 위상공간 \(X\)와 그 부분공간 \(A\)가 주어졌다 하자. Canonical inclusion \(\iota:A\rightarrow X\)에 대하여, 식 \(r\circ\iota=\id_A\)를 만족하는 연속함수 \(r:X\rightarrow A\)가 존재한다면 \(r\)을 부분공간 \(A\)로의 (continuous) retraction_수축이라 부르고, 이 때 \(A\)를 \(X\)의 retract_수축이라 부른다.

집합론의 관점에서 위의 조건을 만족하는 함수 \(r\)은 항상 존재하지만, 핵심은 이 함수 \(r\)이 연속이라는 것이다.

예시 8 가령 2차원 상의 꽉 찬 원판 \(D^2\)와 그 경계 \(S^1\)에 대하여, \(D^2\)에서 \(S^1\)으로의 retraction이 존재하지 않음이 알려져 있다. 만일 retraction \(r:D^2\rightarrow S^1\)이 존재한다면, \(H_n\)의 functoriality로부터

\[H_n(r)\circ H_n(\iota)=H_n(r\circ\iota)=H_n(\id_{S^1})=\id_{H_n(S^1)}\]

이 모든 \(n\)에 대해 성립할 것이다. 특히 \(H_n(\iota):H_n(S^1)\rightarrow H_n(D^2)\)는 injective여야 한다. 그런데 §호몰로지, ⁋예시 8에서 우리는 \(H_1(D^2)\cong 0\)임을 보였고, \(D^2\setminus \left\{(0,0)\right\}\)의 계산을 따라하면 \(H_1(S^1)\neq 0\)임을 알 수 있으므로, injective homomorphism \(H_1(\iota)\)가 존재할 수 없다.

그런데 이 예시와 §호몰로지, ⁋예시 8에서의 \(D^2\setminus \left\{(0,0)\right\}\)의 호몰로지의 계산을 비교해보면, \(D^2\setminus \left\{(0,0)\right\}\)에서 나타날 수 있는 nontrivial한 호몰로지는 결과적으로 그 부분집합인 \(S^1\)에서도 동일하게 나타난다는 것을 알 수 있다. 우리는 명제 6에 의하여 homotopic한 연속함수가 homotopic한 chain map을 유도하는 것을 알고, 따라서 이들이 호몰로지 위에서 같은 함수를 유도하는 것을 알고 있으므로, 이를 어떻게 일반화해야할지는 자명하다.

정의 9 위상공간 \(X\)와 그 부분공간 \(A\)가 주어졌다 하고, \(r:X\rightarrow A\)가 retraction이라 하자. 만일 \(\id_X\)에서 \(r\)로의 homotopy \(F\)가 존재한다면, 이를 \(A\)로의 deformation retraction_{변형 수축}이라 부르고, \(A\)를 \(X\)의 deformation retract_{변형 수축}이라 부른다.

그럼 위의 예시 8에서의 retraction \(r\)에 대하여, 다음의 식

\[t\frac{\mathbf{x}}{\lvert\mathbf{x}\rvert}+(1-t)\mathbf{x}\]

으로 정의하면 이것이 \(\id_X\)에서 \(r\)로의 homotopy를 정의한다. 즉 \(S^1\)은 \(D^2\setminus \left\{(0,0)\right\}\)의 deformation retract이다.

Fundamental group

우리는 §호몰로지, ⁋예시 8에서, 만일 \(1\)-simplex \(\Delta^1\)을 \(I=[0,1]\)로 본다면 \(C_1(X)\)을 생성하는 원소들을 그 정의에 의해 \(X\) 위에서의 path로 생각할 수 있다고 하였으며, 이로부터 homology \(H_1(X)\)를 얻어낼 때, 우리는 closed path들을 생각하게 된다. 이는 본질적으로 \(S^1\)에서 \(X\)로의 함수들을 보는 것과 같다. 이를 더 엄밀하게 다뤄보자.

우선 두 homotopic한 연속함수 \(f,g:X \rightarrow Y\)와 이들 사이의 homotopy \(F\)에 대하여, 만일 부분집합 \(A\subseteq X\)에 대해 다음의 식

\[F(x,t)=f(x)\qquad\text{for all $t\in[0,1]$}\]

이 성립한다면 \(F\)가 homotopy relative to \(A\)라 말한다. 만일 정의 9에서, homotopy \(F\)가 homotopy relative to \(A\)라면 우리는 \(A\)가 \(X\)의 strong deformation retract라 부른다.

이제 임의의 두 path \(\alpha_0,\alpha_1:I\rightarrow X\)에 대하여, 이들 사이의 path homotopy는 것은 homotopy relative to \(\{0,1\}\)를 의미한다. 즉, 두 path \(\alpha_0,\alpha_1\)가 끝점들을 공유하며 (즉 \(\alpha_0(0)=\alpha_1(0)\)이고 \(\alpha_0(1)=\alpha_1(1)\)이며) homotopy \((\alpha_t)_{0\leq t\leq 1}\)가 끝점들을 보존하여

\[\alpha_0(0)=\alpha_t(0)=\alpha_1(0),\qquad \alpha_0(1)=\alpha_t(1)=\alpha_1(1)\qquad\text{for all $0\leq t \leq 1$}\]

인 것이다.

정의 10 만일 두 path \(\alpha_0,\alpha_1:I\rightarrow X\) 사이의 path homotopy가 존재한다면, 이들이 path homotopic하다고 말하고 \(\alpha_0\sim \alpha_1\)로 표기한다.

그럼 명제 3의 증명을 약간 활용하여 path homotopy가 끝점 \(p,q\)를 갖는 path들의 집합에 equivalence relation을 주는 것을 안다. 뿐만 아니라, 이 equivalence relation은 reparametrization을 보존하는 것 또한 자명한데, 임의의 path \(\alpha:I \rightarrow X\)와 임의의 reparametrization \(\varphi:I\rightarrow I\) (즉, \(0,1\)을 보존하는 homeomorphism)에 대하여

\[\alpha_t(s)=\alpha(t\varphi(s)+(1-t)s)\]

로 정의하면 이것이 \(\alpha_0=\alpha\)와 \(\alpha_1=\alpha\circ\varphi\) 사이의 path homotopy이기 때문이다. 이를 사용하면 우리는 두 path의 곱을 다음의 식

\((\alpha\ast \beta)(s)=\begin{cases}\alpha(2s)&0\leq s \leq 1/2\\ \beta(2s-1)&1/2\leq s \leq 1\end{cases}\tag{\)\ast\ast\(}\)

으로 정의한다. 이것이 continuous path가 되기 위해서는, 물론 \(*\)는 \(\alpha(1)=\beta(0)\)를 만족해야 한다. 그럼 다음 성질들이 성립한다.

1. 만일 \(\alpha_0\sim \alpha_1\)이고 \(\beta_0\sim \beta_1\)이며 \(\alpha_0\ast \beta_0\)이 잘 정의된다면, \(\alpha_1\ast \beta_1\)도 잘 정의되며 \(\alpha_0\ast \beta_0\sim \alpha_1\ast \beta_1\)이 성립한다. 이는 homotopy \(\alpha_t\ast \beta_t\)를 생각하면 자명하다.
2. 따라서 \(C(I,X)\)에 path homotopy로 equivalence relation을 주면 식 \([\alpha]\ast[\beta]=[\alpha\ast \beta]\)을 통하여, \(\alpha(1)=\beta(0)\)을 만족하는 \(\alpha,\beta\)마다 \([\alpha]\)와 \([\beta]\)의 연산이 잘 정의된다.
3. 그럼 점 \(\alpha(0)\)과 점 \(\alpha(1)\)에 머무르는 constant path들 \(c_{\alpha(0)}\)과 \(c_{\alpha(1)}\)에 대하여 \([c_{\alpha(0)}]\ast [\alpha]=[\alpha]=[\alpha]\ast[c_{\alpha(1)}]\)이 성립한다. 이는 대략적으로 path homotopy는 reparametrization을 보존하므로 식 (\(\ast\ast\))에서 \(1/2\)를 \(0\)과 \(1\) 사이의 아무 숫자로 바꾸어도 되고, 이 숫자를 \(0\) 혹은 \(1\)로 접근시키는 것이 원하는 homotopy를 주기 때문이다. 거의 같은 논리로 \(\ast\)가 associative라는 것을 보일 수 있다.
4. 뿐만 아니라 역원도 존재하는데, 임의의 path \(\alpha\)에 대해 \(\bar{\alpha}(t)=\alpha(1-t)\)로 정의하면 \([\alpha]\ast[\bar{\alpha}]=[c_{\alpha(0)}]\)이고 \([\bar{\alpha}]\ast[\alpha]=[c_{\alpha(1)}]\)이 성립한다.

이 결과들을 정리하면 다음과 같다.

정의 11 위의 결과들에 의해 \(C(I,X)/{\sim}\)은 groupoid를 이루며, 이를 \(X\)의 fundamental groupoid라 부르고 \(\Pi_1(X)\)로 적는다. ([범주론] §범주, ⁋정의 11)

즉 임의의 공간 \(X\)에 대하여, fundamental groupoid \(\Pi_1(X)\)는 \(X\)의 점들을 object로, 두 점 \(x,y\)에 대해 \(x\)에서 \(y\)로의 path들의 homotopy type을 morphism으로 갖는 category이다. \(\Cat\)의 full subcategory로서, \(\Grpd\)에서의 morphism은 그냥 functor이다. 명시적으로, 임의의 continuous map \(f:X \rightarrow Y\)가 주어졌을 때 \(\Pi_1(f):\Pi_1(X)\rightarrow\Pi_1(Y)\)는 object에 대해서는 \(x\mapsto f(x)\)로 정의되고, morphism에 대해서는 합성

\[\Pi_1(f)([\alpha])=[f\circ\alpha]\]

로 정의되며, 이것이 잘 정의된다는 것은 두 path \(\alpha_0\sim\alpha_1\)에 대하여, \(\alpha_t\)가 이들 사이의 path homotopy라면 \(f\circ \alpha_t\)가 \(f\circ\alpha_0\)과 \(f\circ\alpha_1\) 사이의 path homotopy이므로 자명하다. 뿐만 아니라, 만일 두 continuous map \(f_0,f_1:X \rightarrow Y\)가 homotopic하다면 이들이 유도하는 두 functor \(\Pi_1(f_0)\)와 \(\Pi_1(f_1)\) 사이의 natural isomorphism이 존재한다. ([범주론] §자연변환, ⁋정의 1) 즉 \(x_0,x_1\)을 각각 시작점과 끝점으로 갖는 임의의 path \(\alpha:I \rightarrow X\)에 대하여, 다음의 diagram

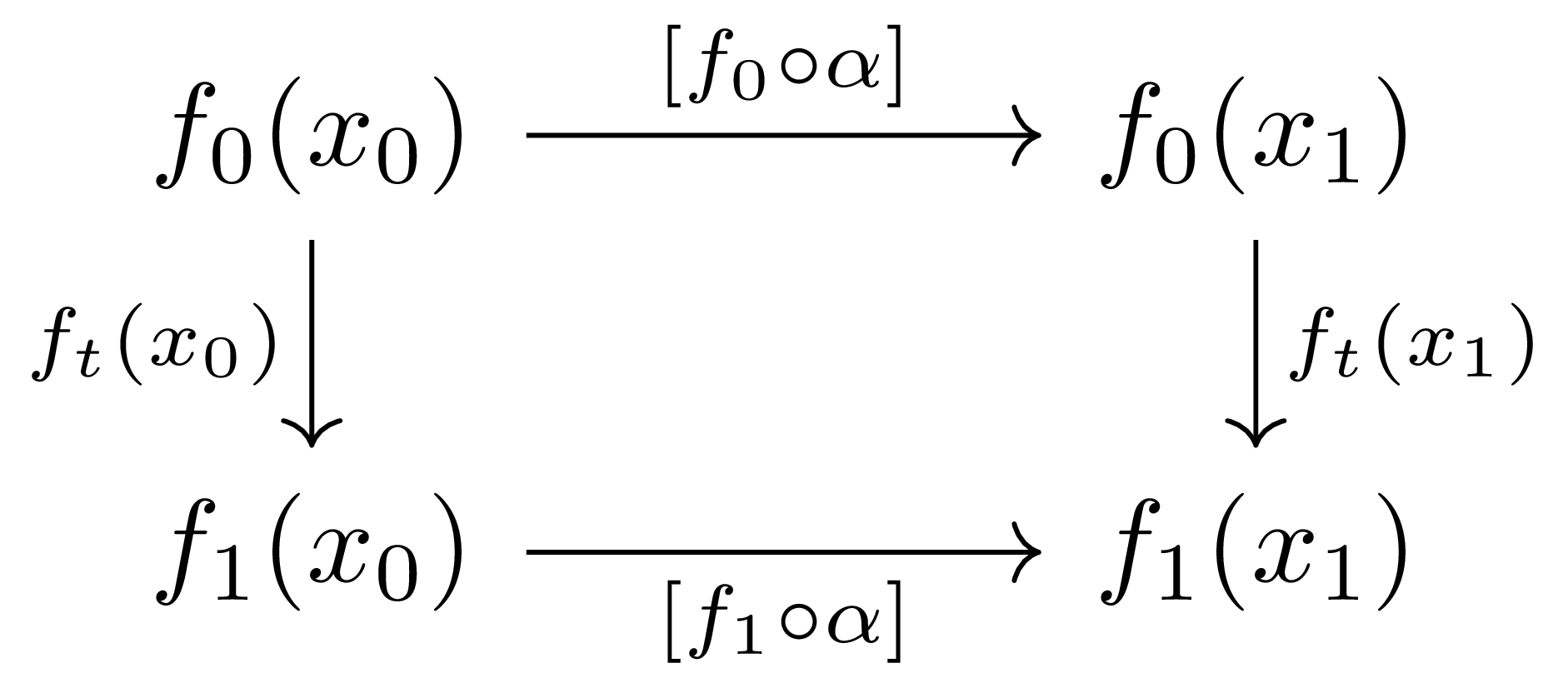
이 commute (up to path homotopy)한다. 여기서 \(f_t(x_0)\)과 \(f_t(x_1)\)은 homotopy \((f_t)_{0\leq t\leq 1}\)에 의해 생기는 path들이며, commutativity는 다음의 path homotopy

\[F(s,t)=f_t(\alpha(s))\]

에 의해 분명하다.

특별히 고정된 점 \(x\in X\)을 시작점과 끝점으로 갖는 path들 (즉 \(x\)를 base point로 갖는 loop들)만을 생각하면, 이는 category \(\Pi_1(X)\)의 \(x\)에서의 endomorphism monoid를 생각하는 것과 같고 \(\Pi_1(X)\)가 groupoid이므로 이는 사실 automorphism group이다. 이를

\[\pi_1(X,x)=\Aut_{\Pi_1(X)}(x)\]

로 적으며, 만일 \(X\)가 path-connected라면 이 group은 \(x\)의 선택에 의존하지 않는다. 이를 \(X\)의 fundamental group이라 부르며, 이는 \(\Pi_1(X)\)의 skeleton이다. ([범주론] §자연변환, ⁋정의 4) 따라서 \(\pi_1(X,x)\)는 category로서 \(\Pi_1(X)\)와 equivalent하다. 그럼 위에서 살펴본 것과 같이, homotopic한 연속함수는 fundamental groupoid 사이의 natural isomorphism을 유도하므로 fundamental groupoid와 fundamental group은 homotopy invariant임을 안다.

예시 12 예를 들어, 공간 \(\mathbb{R}^n\)의 fundamental groupoid \(\Pi_1(\mathbb{R^n})\)는 다음의 데이터로 이루어진 category이다.

• \(\Pi_1(\mathbb{R}^n)\)의 object는 정확히 \(\mathbb{R}^n\)의 점들이다.

• 임의의 \(\mathrm{x}_1,\mathrm{x}_2\in \mathbb{R}^n\)에 대하여, \(\mathrm{x}_1\)에서 \(\mathrm{x}_2\)로의 유일한 morphism이 존재한다. 즉 \(\mathrm{x}_1\)에서 시작하여 \(\mathrm{x}_2\)로 가는 임의의 path \(\alpha_1:I \rightarrow \mathbb{R}^n\)은 항상 다음의 path

  \[\alpha_0:t\mapsto (1-t)\mathrm{x}_1+t\mathrm{x}_2\]

  와 path homotopic하다. 이는 \(\alpha_t=(1-t)\alpha_1+t\alpha_0\)으로 두면 쉽게 확인할 수 있다.

따라서, 임의의 \(\mathrm{x}\)에 대하여 \(\pi_1(\mathbb{R},\mathrm{x})\)는 trivial group이다.

---

참고문헌

[Hat] A. Hatcher, Algebraic Topology. Cambridge University Press, 2022.
[Mun] James Munkres, Topology. Prentice Hall, 2000.

---