피복공간

이전 글에서 우리는 fundamental group $\pi_1(X)$를 정의하고 간단한 성질들을 살펴보았다. 그럼 정의들로부터 다음 보조정리는 거의 자명하다.

보조정리 1 Path-connected space $X$에 대하여, 다음이 모두 동치이다.

끝점을 공유하는 임의의 두 path $p,q$는 항상 path homotopic하다.
임의의 loop $f:S^1 \rightarrow X$는 항상 null-homotopic이다.
임의의 loop $f:S^1 \rightarrow X$에 대하여, 적당한 continuous map $\widetilde{f}:D^2 \rightarrow X$가 존재하여 $\widetilde{f}$의 domain을 그 boundary $S^1$로 제한한 것이 $f$이도록 할 수 있다.
$\pi_1(X)=0$이다.

증명

첫째 조건, 둘째 조건과 마지막 조건이 동치라는 것은 두 path $p,q$에 대하여 loop $p\ast\bar{q}$를 생각하면 자명하다. 따라서 셋째 조건과 이들이 동치임을 보이면 충분하다.

우선 첫째 조건을 가정하여, 임의의 loop $f:S^1 \rightarrow X$에 대하여 적당한 homotopy $(f_t)$가 존재하여 $f_1=f$이고 $f_0$은 고정된 점 $x_0$으로의 constant map이도록 할 수 있다. 그럼 다음 식

\[\widetilde{f}(\mathrm{x})=\begin{cases}f_{\lvert\mathrm{x}\rvert}(\mathrm{x}/\lvert\mathrm{x}\rvert)&\text{if $\lvert\mathrm{x}\rvert\neq 0$}\\ x_0&\text{if $\lvert\mathrm{x}\rvert=0$}\end{cases}\]

이 셋째 조건에서 요구하는 연속함수라는 것을 알 수 있다. 거꾸로 셋째 조건을 가정하면, 임의의 loop $f$가 주어졌을 때 $f_t(\mathrm{x})=\widetilde{f}(t\mathrm{x})$로 둔 것이 $f_1=f$에서 constant map으로의 homotopy가 된다.

정의 2 만일 보조정리 1의 동치조건들이 성립한다면, path-connected $X$를 simply connected space_{단순연결공간}이라 부른다.

남은 글에서 우리는 편의상 path-connected space들만 생각한다. Simply connnected가 아닌 공간의 fundamental group을 계산하기 위해서는 여러 방법이 필요한데, 가장 기초적이고 핵심적인 방법 중 하나는 covering space를 사용하는 것이다.

정의 3 Continuous surjection $p:E \rightarrow B$에 대하여, $B$의 열린집합 $U$가 $p$에 의해 evenly covered_{고르게 덮임}이라는 것은 $p^{-1}(U)$가 $U$와 homeomorphic한 $E$의 disjoint open set들의 합집합으로 쓰여지는 것이다. 만일 임의의 $x\in B$마다 $p$에 의해 evenly covered인 적당한 open neighborhood $U$가 존재한다면 $p$를 covering map이라 부르고, $E$를 covering space_피복공간라 부른다.

정의는 다소 복잡하지만, 본질적으로는 다음의 그림을 염두에 두면 편하다.

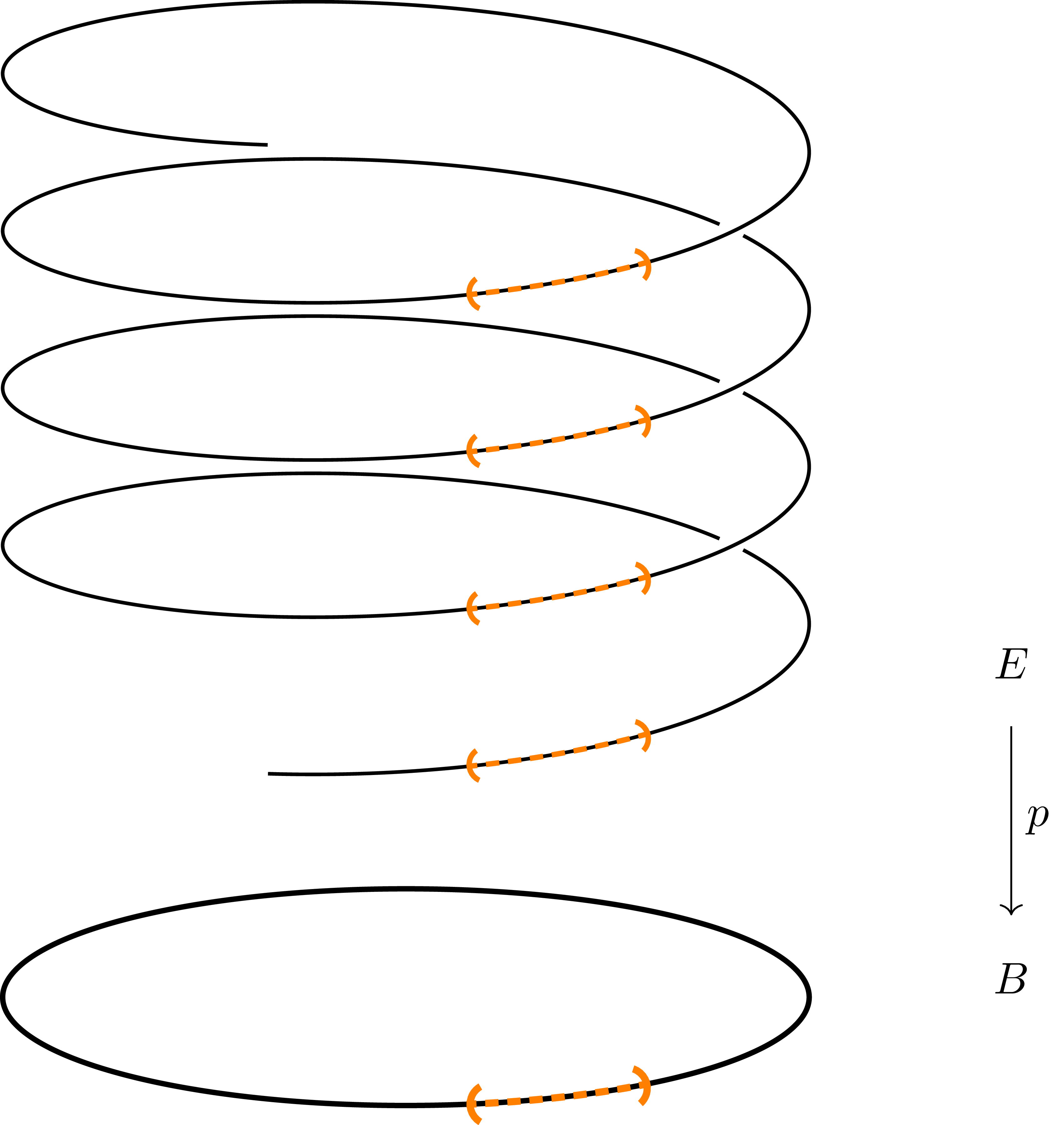
$S1_covering$

이는 covering map

\[p:\mathbb{R}\rightarrow S^1;\quad t\mapsto (\cos 2\pi t, \sin 2\pi t)\]

를 나타낸 것이며, 이것이 정의 2의 조건을 만족하는 것을 안다. 한편 일반적인 경우, covering map은 다음과 같이 부분공간과 곱공간에 대해 잘 작동한다는 것을 쉽게 증명할 수 있다.

명제 4 다음이 성립한다.

Covering map $p:E \rightarrow B$와 $B$의 부분공간 $A$에 대하여, $p\vert_{p^{-1}(A)}:p^{-1}(A) \rightarrow A$는 covering map이다.
두 covering map $p_1:E_1 \rightarrow B_1$, $p_2:E_2\rightarrow B_2$에 대하여, $p_1\times p_2:E_1\times E_2 \rightarrow B_1\times B_2$는 covering map이다.

피복공간의 기본정리

Fundamental groupoid $\Pi_1:\Top \rightarrow \Grpd$의 functoriality를 이용하면, 임의의 연속함수 $p:E \rightarrow B$는 다음의 groupoid homomorphism

\[\Pi_1(f):\Pi_1(E) \rightarrow \Pi_1(B)\]

을 정의한다. 특히 임의의 $y_0, y_1\in E$에 대하여, 다음의 homomorphism

\[\Hom_{\Pi_1(E))}(y_0, y_1)\rightarrow \Hom_{\Pi_1(B)}(p(y_0), p(y_1))\tag{$\ast$}\]

이 잘 정의된다. 만일 $B$가 path-connected이고 $p(y_0)=p(y_1)$라면, 이는 fundamental group $\pi_1(B)$로의 (groupoid) homomorphism이 될 것이다. 만일 $E$가 $B$의 fundamental group (혹은 groupoid)에 대한 정보를 모두 가지고 있다면 적어도 이 homomorphism이 surjective여야 한다.

정의 5 Continuous map $p:E\rightarrow B$를 고정하자. 그럼 임의의 continuous map $f:X \rightarrow B$에 대하여, $f$의 $p$에 대한 lifting이란 식 $p\circ\widetilde{f}=f$를 만족하는 $\widetilde{f}:X\rightarrow E$를 의미한다.

이러한 정의를 생각하는 이유는 당연히 $X=I$이고 따라서 $f$가 $B$로의 path일 경우, 만일 $f$의 $p$에 대한 lifting이 존재한다면 이것이 homomorphism ($\ast$)에 의한 $f$의 preimage에 속하기 때문이다. 그렇다면 우리의 주장은 만일 $p$가 covering space라면 이러한 lifting이 항상 존재한다는 것이다.

보조정리 6 Covering map $p:E \rightarrow B$와 $E$의 임의의 한 점 $y_0$를 생각하자. 그럼 $x_0=p(y_0)$에서 시작하는 임의의 path $\alpha:I \rightarrow B$가 주어질 때마다, $y_0$에서 시작하는 lifting $\widetilde{\alpha}:I \rightarrow E$가 유일하게 존재한다.

증명

우선 $p$가 covering space라는 가정으로부터, $B$의 open covering $(U_i)$이 존재하여 각각의 $U_i$들이 $p$에 의해 evenly covered이도록 할 수 있다. 이제 $(\alpha^{-1}(U_i))$는 $I$의 open covering이므로 $I$를 덮는 finite subcover가 존재한다. 이제 ##ref##를 사용하여, $I$의 subdivision

\[0=s_0<s_1<\cdots<s_n=1\]

을 찾아 $\alpha([s_i,s_{i+1}])$이 $U$ 안에 들어가도록 할 수 있다. 이제 $\widetilde{\alpha}(0)=y_0$으로 정의하고, 귀납적으로 $\widetilde{\alpha}$를 정의하기 위해 $0\leq s\leq s_i$에 대해 $\widetilde{\alpha}$가 정의되었다 가정하고 $[s_i,s_{i+1}]$에서 $\widetilde{\alpha}$를 정의하자. 우선 $s_i$들의 선택에 의해 $\alpha([s_i,s_{i+1}])$이 $p$에 의해 evenly covered인 열린집합 $U$에 들어간다. 따라서, $p^{-1}(U)$를 $U$와 homeomorphic한 열린집합들의 disjoint union $\coprod_{j\in J}V_j$으로 쓸 수 있다. 이제 $\widetilde{\alpha}(s_i)\in V_j$이도록 하는 $V_j$에 대하여, $\widetilde{\alpha}$를 다음의 식

\[\widetilde{\alpha}(s)=(p\vert_{V_j})^{-1}(\alpha(s))\]

으로 정의해주면 된다. 유일성의 경우, $[s_i,s_{i+1}]$이 connected이고, 귀납적으로 $\alpha(s_i)$가 속하는 component가 차례차례 정해지므로 자명하다.

증명은 다소 기술적으로 보일 수 있지만, 핵심 아이디어는 $x_0\in B$에서 시작하는 임의의 path는 적어도 짧은 시간 동안에는 $p$에 의해 evenly cover되는 $x_0$의 열린근방 $U$에 들어있을 것이고, 정의에 의해 $p^{-1}(U)$는 $U$와 homeomorphic한 $E$의 disjoint open subset들의 합집합이며 따라서 시작점이 이들 중 어디에 속해있는지만 알면 (연결성에 의해) 이 짧은 시간동안 path가 머무는 component가 어떤 것인지가 정해진다는 것이다. Lebesgue number lemma는 이 과정이 유한하다는 것을 보일 때만 쓰였다.

다시 ($\ast$)의 groupoid homomorphism을 보자. 보조정리 6에 의하여, covering space $p:E \rightarrow B$에서 임의의 $x_0,x_1\in B$와 이들을 끝점으로 하는 path $\alpha$가 주어졌다 하면, $y_0\in p^{-1}(x_0)$의 선택은 $y_1\in p^{-1}(x_1)$과 $\widetilde{\alpha}\in \Hom_{\Pi_1(E)}(y_0,y_1)$을 결정한다. 그렇다면 자연스러운 질문은 만일 $\alpha$와 path-homotopic한 $\alpha'$에 대하여, 동일한 $y_0$의 선택이 동일한 $y_1$과 homotopy type을 주는지의 여부일 것이다. 만일 $p$가 covering space라면 이에 대한 답도 긍정적이다.

보조정리 7 Covering map $p:E \rightarrow B$와 $E$의 임의의 한 점 $y_0$을 생각하고 $p(y_0)=x_0$이라 하자. 그럼 $F(0,0)=x_0$을 만족하는 연속함수 $F:I\times I \rightarrow B$가 주어질 때마다, $\widetilde{F}(0,0)=y_0$을 만족하는 lifting $\widetilde{F}:I\times I \rightarrow E$가 유일하게 존재한다. 뿐만 아니라, 만일 $F$가 path homotopy라면 $\widetilde{F}$도 path homotopy이다.

이에 대한 증명은 본질적으로 보조정리 6와 다를 것이 없으므로 생략하기로 한다. 중요한 것은 이 보조정리가 주는 path homotopy에 의하여, covering space $p:E \rightarrow B$와, path class $[\alpha]\in\Hom_{\Pi_1(B)}(x_0,x_1)$이 주어졌다 하면 $y_0\in p^{-1}(x_0)$의 선택이 $E$의 path class $[\widetilde{\alpha}]\in \Hom_{\Pi_1(E)}(y_0,y_1)$을 유일하게 결정한다는 것이다.

이제 다시 fundamental groupoid $\Pi_1(B)$를 생각하고, covering map $p:E \rightarrow B$을 고정하자. 그럼 evenly covered 조건에 의해, 각각의 $x\in B$에 대하여 $p^{-1}(x)$는 discrete set이다. 이 때 임의의 path class $[\alpha]\in\Hom_{\Pi_1(B)}(x_0,x_1)$에 대하여, $y_0\in p^{-1}(x_0)$을 택하면 보조정리 7는 유일한 path class $[\widetilde{\alpha}]$를 정의하고, 따라서 $y_1\in p^{-1}(x)$를 정의한다. 즉 $[\alpha]$는 함수 $p^{-1}(x_0)\rightarrow p^{-1}(x_1)$를 정의한다.

정의 8 위와 같은 상황에서, 함수 $p^{-1}(x_0)\rightarrow p^{-1}(x_1)$을 transport map이라 부르고 $T_{[\alpha]}$로 적는다.

Transport map은 bijective이다. 이는 우선, 임의의 $y_1\in p^{-1}(x_1)$이 주어진다면 우리는 path class $[\overline{\alpha}]\in\Hom_{\Pi_1(B)}(x_1,x_0)$를 사용하여 $y_1$에서 시작하고 $p^{-1}(x_0)$의 어떤 원소 $y_0$에서 끝나는 path를 찾을 수 있으며, 이러한 과정이 보조정리 7에 의해 유일하기 때문이다. 비슷하게, lifting의 유일성에 의하여 이러한 대응이 path의 concatenation을 잘 보존한다는 것을 안다. 즉 $x\in \Pi_1(B)$를 $p^{-1}(x)$로, $[\alpha]\in\Hom_{\Pi_1(B)}(x_0,x_1)$을 $T_{[\alpha]}:p^{-1}(x_0)\rightarrow p^{-1}(x_1)$로 보내는 대응은 functorial하다.

정의 9 위에서 정의한 functor $\Pi_1(B) \rightarrow \Set$을 $p$가 정의하는 monodromy functor라 부르고 $M_p$로 표기한다.

고정된 base space $B$에 대하여, 우리는 자명한 방식으로 $B$의 covering space들의 category $\Cov(B)$를 정의한다. 명시적으로 이 category의 object들은 covering map들 $p:E\rightarrow B$이고, 이를 사이의 morphism은 다음의 commutative diagram

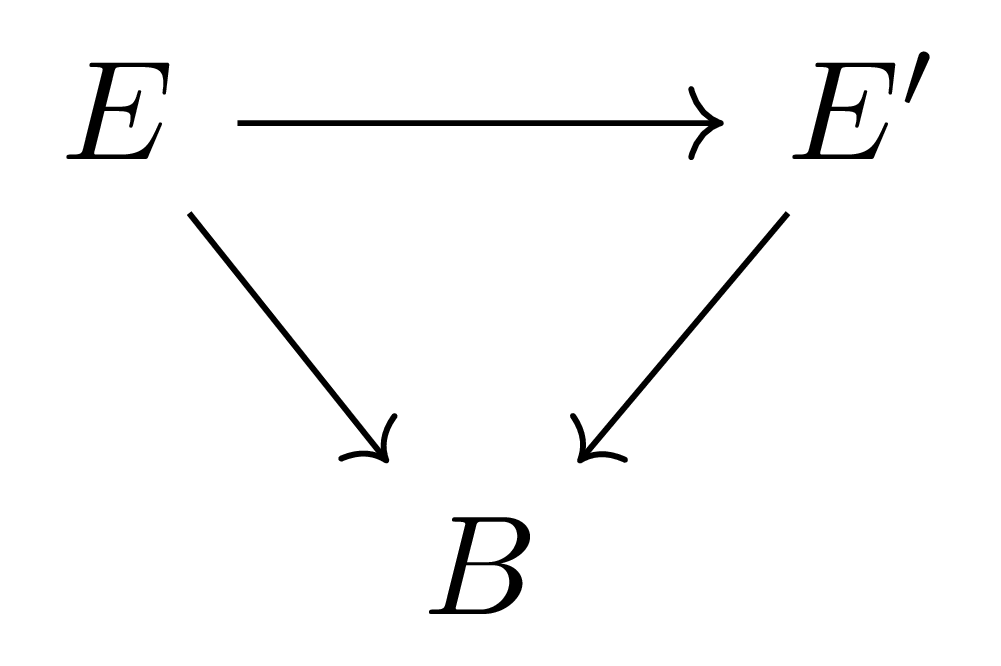
$morphism_of_covering_spaces$

이다. 이를 통해, 각각의 $p\in \Cov(B)$마다 monodromy functor $M_p$를 대응시키는 것이 functor

\[M:\Cov(B) \rightarrow \Fun(\Pi_1(B),\Set)\]

를 정의하는 것을 알 수 있으며, 이번 글의 핵심 결과는 이것이 두 category 사이의 equivalence라는 것이다. 이를 보이기 위해서는 우선 위의 대응의 functoriality부터 시작하여, 보여야 할 것이 많지만 결과적으로 가장 핵심적인 내용은 임의의 functor $\Pi_1(B)\rightarrow \Set$이 주어졌을 때 이로부터 covering space $E \rightarrow B$를 만드는 것이다. 이를 위해 임의의 functor $F:\Pi_1(B) \rightarrow \Set$이 주어졌다 하면, 위의 monodromy functor를 거꾸로 따라가보면 $p:E\rightarrow B$를 집합 사이의 함수로서 어떻게 만들어야 하는지는 자명하다. 각각의 $x\in \Pi_1(B)$에 대하여, $F(x)$는 $x$에서의 $p$의 fiber에 해당할 것이므로 projection

\[p:E=\coprod_{x\in B}F(x) \rightarrow B\]

로 잡으면 된다. 문제는 이것이 covering space가 되도록 하는 위상구조를 $E$ 위에 부여하는 것이다. 만일 이러한 위상구조가 존재한다면 $x$의 open neighborhood $U$가 존재하여 $p^{-1}(U)$와 $U\times F(x)$ 사이의 homeomorphism이 존재해야 할 것이다. 우리에게 익숙한 $\mathbb{R}\rightarrow S^1$을 생각하면 이는 직관적으로 자명한데, $p^{-1}(U)$는 $U$와 homeomorphic한 집합들의 disjoint union이며 따라서 $p^{-1}(U)$의 임의의 원소는 이 원소가 이러한 집합들 중 어디에 들어있는지 ($F(x)$), 그리고 그 집합의 어떤 점인지 ($U$)에 의해 결정되기 때문이다. 우리는 거꾸로 bijection $\phi:p^{-1}(U) \rightarrow U\times F(x)$을 만들어 이를 이용하여 $p^{-1}(U)$ 위에 위상구조를 정의할 것이다. 그럼 이들 $\phi$들이 겹치는 부분에서는 같은 함수를 정의하고, 따라서 이 bijection들이 $E$ 위에 적절한 위상구조를 주며 이것이 우리가 원하는 성질을 만족한다는 것을 보이는 것은 단순한 노동이며, 증명의 핵심은 $\phi$를 정의하는 부분이다.

위에서 정의한 $p$의 형태에 의하여, 우리는 $p^{-1}(U)$는 $x'\in U$를 만족하는 $x'$들에 대하여, $F(x')$들의 모임임을 안다. 그럼 $\phi(x')$의 첫 번째 좌표는 당연히 $x'$ 자기 자신이 나와야 할 것이며 둘째 좌표는 transport map을 생각하면 $x'$와 path로 이어지는 $F(x)$의 원소가 되어야 할 것이다. 그런데 이를 위해서는 이 정보가 $\Pi_1(B)$에 들어있어야 하므로, 우리는

$U$가 path-connected가 되어 $x$와 $x'$를 잇는 path class $[\alpha]\in \Hom_{\Pi_1(B)}(x,x')$가 항상 존재하며,
이러한 path class가 유일하게 결정되어야 한다는 것을 안다.

첫째 조건은 $B$가 locally path-connected라는 것 뿐이다. 둘째 조건은 조금 더 미묘한데, $U$ 안에서 끝점을 공유하는 두 path가 $B$에서 같은 path class를 정의하면 된다. 이는 locally simply connected보다 더 약한 조건이다.

정의 10 위상공간 $X$가 semi-locally simply connected라는 것은 임의의 $x\in X$마다 적당한 open neighborhood $U$가 존재하여 $U$의 임의의 loop가 $X$에서 contractible이도록 할 수 있는 것이다.

그럼 위의 논증이 성립하기 위해서는 공간 $B$가 기존에 가정했던 path-connected 조건 외에도 두 조건 locally path-connected, semi-locally simply connected 조건을 만족해야 하는 것을 안다. 이제 위의 논의를 종합하면 다음의 결과를 얻는다.

정리 11 (Fundamental theorem of covering spaces) Path-connected, locally path-connected, semi-locally simply connected space $B$에 대하여, 두 category 사이의 equivalence

\[M:\Cov(B) \rightarrow \Fun(\Pi_1(B), \Set)\]

이 존재한다.

예를 들어 임의의 path-connected topological manifold는 항상 위의 조건을 만족한다.

이제 $\Fun(\Pi_1(B), \Set)$이 무엇인지 살펴보아야 한다. 더 일반적으로 임의의 groupoid $\mathscr{G}$에 대하여 functor $\mathscr{G}\rightarrow \Set$이 무엇인지를 생각해보자. 이는 정의에 의해

$\mathscr{G}$의 각각의 object $G\in \mathscr{G}$에 대응되는 집합 $S_G$,
$\mathscr{G}$의 각각의 (iso)morphism $G \rightarrow H$마다 대응되는 bijection $S_G \rightarrow S_H$

로 이루어진다. 이것만으로는 여전히 functor $\mathscr{G}\rightarrow \Set$이 무엇인지 보이지 않으니 특별히 $\mathscr{G}$가 하나의 object $\ast$만을 가지고 따라서 $\mathscr{G}$의 모든 morphism들이 $\ast$의 automorphism이 되는 상황을 보자. 즉 $\mathscr{G}$는 group이다. 그럼 이 가정 하에서, functor $\mathscr{G}\rightarrow \Set$은 다음의 데이터이다.

$\mathscr{G}$의 유일한 object에 대응되는 집합 $S$,
임의의 automorphism $g:\ast \rightarrow \ast$에 대응되는 bijection $g\cdot-: S\rightarrow S$.

즉, 표기에서 짐작할 수 있듯 이 정보는 정확하게 group $\mathscr{G}$의 action이며, $\Fun(\mathscr{G},\Set)$은 정확히 $\mathscr{G}$-set들의 모임이고 이들 사이의 morphism은 $\mathscr{G}$-equivariant map들이다. 일반적인 groupoid $\mathscr{G}$에 대하여는 그저 여러 개의 group이 여러 개의 집합에 따로따로 act하되, isomorphic한 $\mathscr{G}$의 두 object $G,H$는 각각의 (isomorphic한) 집합 $S_G$와 $S_H$에 같은 방식으로 act해야 하는 것이다.

그런데 공간 $B$가 path-connected이므로, fundamental groupoid $\Pi_1(B)$는 connected groupoid이고 따라서 $\Pi_1(B)$는 임의의 $x\in B$에 대하여 group $\pi_1(B,x)$와 category로서 equivalent하다. 즉 $\Pi_1(B)$의 groupoid action은 group $\pi_1(B,x)$의 group action을 groupoid $\Pi_1(B)$에서의 isomorphism을 따라 복제한 것에 불과하다. 따라서 위의 정리 11에 담겨있는 정보는 본질적으로 skeleton에 담겨있다. 따라서

\[\sk(M):\sk(\Cov(B))\rightarrow \sk(\Fun(\Pi_1(X), \Set))\]

을 생각하자. 이는 covering space들의 isomorphism class를 받아 monodromy functor $M_p$를 up to natural isomorphism으로 내놓는 equivalence이다. 즉, $\Pi_1(X)$-sets up to isomorphism이다. 일반적으로

\[\sk(\Fun(\Pi_1(X),\Set))\simeq\Fun(\sk(\Pi_1(X)), \Set)\]

이므로, 다시 여기에서 $X$가 path-connected임을 이용하면 우리는 covering space들의 isomorphism class를 받아 $\pi_1(X,x)$-set을 내놓는 categorical equivalence가 존재함을 안다.

그런데 [대수적 구조] §군의 작용, ⁋정리 14와 그 증명을 생각하면, 임의의 $G$-set $E$가 주어졌을 때 우리는 $E$를 $G$의 orbit들로 분해할 수 있고, 그럼 이들 각각의 orbit들로 제한했을 때의 $G$-action은 transitive하며 이들은 $G$의 적당한 normal subgroup $N$에 대하여, canonical $G$-action이 주어진 $G/N$과 isomorphic하다. 따라서 transitive group action만 생각하기로 한다면, monodromy functor의 정의에 의해 이는 target에서는 connected cover들만 생각하는 것이 된다. 즉 다음의 equivalence

\[\left\{\text{isomorphism classes of covering spaces of $B$}\right\}\simeq \left\{\text{transitive $\pi_1(B,x)$-sets}\right\}\]

가 존재하며, 다시 transitive $\pi_1(B,x)$-set들을 isomorphism에 대해 분류한 skeleton category를 생각하면 최종적으로 다음의 equivalence

\[\left\{\text{isomorphism classes of covering spaces of $B$}\right\}\simeq \left\{\text{conjugacy classes of subgroups of $\pi_1(B,x)$}\right\}\]

를 얻는다. 이제 이들 각각의 category를 살펴보면, 이들은 그저 partially ordered set에 불과하며 ([범주론] §범주, ⁋예시 3) 이 equivalence는 poset 사이의 isomorphism임을 안다. 즉 다음의 결과를 얻는다.

따름정리 12 (Fundamental theorem of covering spaces, classical version) Path-connected, locally path-connected, semi-locally simply connected space $B$에 대하여, connected covering space들의 isomorphism class들의 집합과, $\pi_1(B)$의 subgroup의 conjugacy class들 사이의 Galois correspondance가 존재한다.

명시적으로, covering space $p:E \rightarrow B$가 주어지면 $\pi_1(p):\pi_1(E)\rightarrow \pi_1(B)$를 통해 subgroup이 정의되며, 이 때 두 transitive $G$-set $X\cong G/H$와 $Y\cong G/K$가 isomorphic한 것은 $H$와 $K$가 서로 conjugate인 것과 동치이므로 위의 결과를 얻는다. 한편 만일 $\pi_1(B,x)$의 subgroup들의 conjugacy class들 대신 명시적인 subgroup들 그 자체를 생각한다면 이는 isomorphic한 covering space 중 하나를 택하는 것이 되고, 이는 정확히 $B$의 base point 하나를 고정한 다음, pointed covering map $p:(E, y)\rightarrow (B,x)$를 생각하여 이들 isomorphism class들의 원소를 따로따로 보는 것과 같다. 즉 다음의 Galois correspondance

\[\left\{\text{isomorphism classes of \textit{pointed} covering spaces of $B$}\right\}\simeq \left\{\text{subgroups of $\pi_1(B,x)$}\right\}\]

이 존재한다. 이를 조금 더 익숙한 형태로 만들면, 우리는 임의의 $H\leq \pi_1(B,x)$에 대하여 이에 대응되는 covering space $E_H$를 만들 수 있고 그럼 $E_H$의 automorphism group $\Aut(E_H/B)$에 대하여

\[\Aut(E_H/B)\cong N_G(H)/H\]

이 성립한다. 이를 $E_H$의 Deck transformation group이라 부른다. 더 일반적으로 (fiber $p^{-1}(x)$의 서로 다른 원소를 택하여 얻어지는) covering space들의 automorphism은 $\pi_1(B,x)$의 subgroup들에 inner automorphism을 취하는 것에 대응되며, 우리는 이를 Deck transformation이라 부른다.

한편 $\pi_1(B,x)$의 subgroup(들의 conjugacy class들)의 poset에는 minimal한 원소 $\left\{e\right\}$가 존재한다. 그럼 위의 Galois correspondance에 의해 여기에 대응되는 universal cover $\widetilde{B}$가 존재한다. 이 covering space의 Deck transformation group은 $\pi_1(B,x)$와 isomorphic하며,

자이페르트-반 캄펜 정리

우리가 알고있는 좋은 공간들은 정의로부터 fundamental group 혹은 homology를 계산할 수도 있지만, 대부분의 경우 이를 정의로부터 계산하는 것은 과도하게 복잡하거나 거의 불가능하다. 우리의 아이디어는 큰 공간의 fundamental group을 계산하기 위해 이를 작은 공간들로 나타내는 것이다.

이러한 방법 중 가장 단순한 것은 공간 $X$가 두 열린집합들의 합집합 $X=U\cap V$로 나타나는 경우일 것이다. 그럼 [위상수학] §준층, ⁋보조정리 1에 의하여 우리는 다음의 diagram

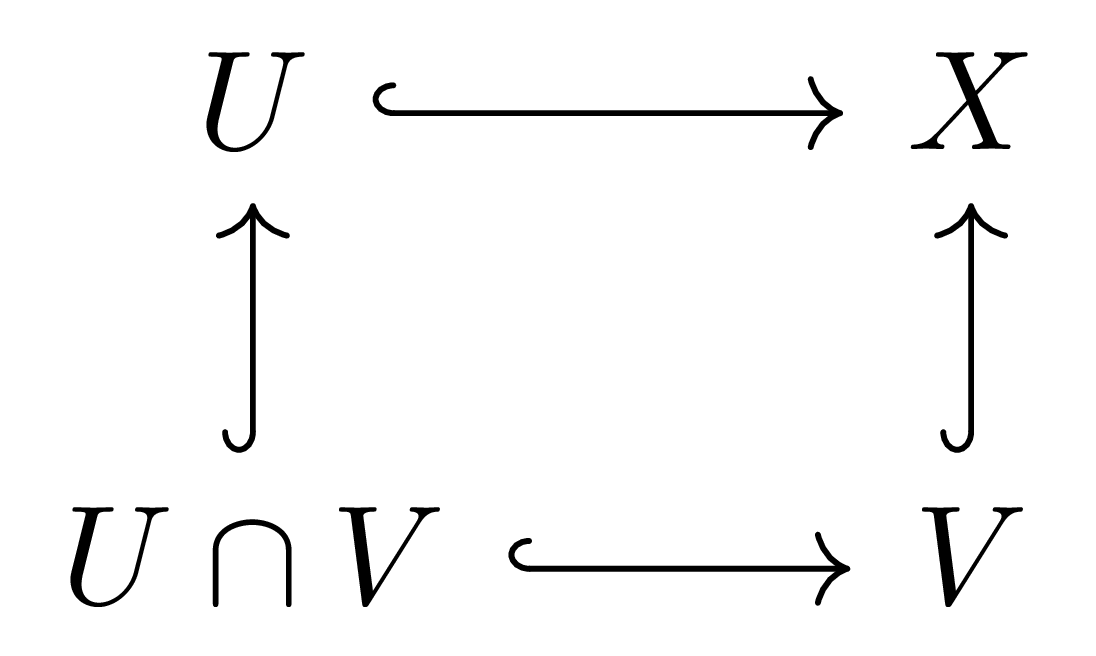
$union_as_colimit$

이 colimit diagram인 것을 안다. 이 경우 우리는 이 diagram에 fundamental groupoid functor $\Pi_1$을 취해 $\Pi_1(X)$를 $\Pi_1(U)$, $\Pi_1(V)$, 그리고 $\Pi_1(U\cap V)$를 이용하여 나타내는 것을 목표로 할 것이다. 한편 [위상수학] §준층, ⁋보조정리 1는 임의의 open covering $(U_i)$에 대하여 다음의 diagram

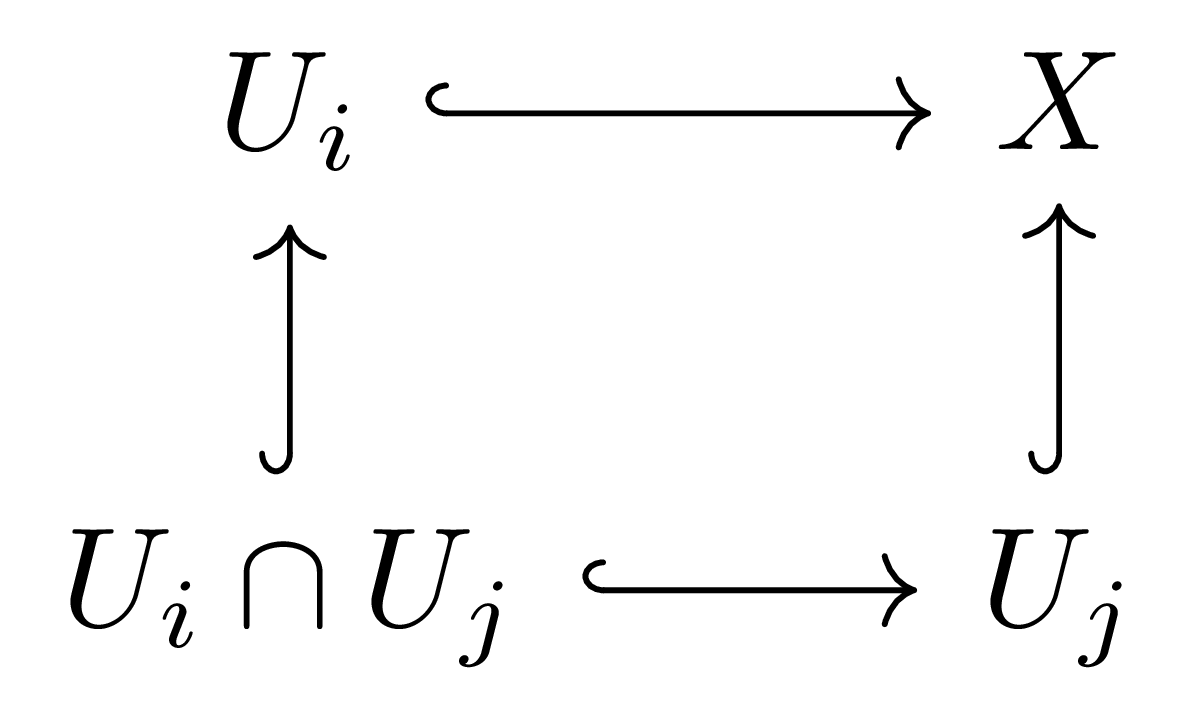
$general_union_colimit$

이 colimit diagram임을 안다. 우리의 주장은 만일 $(U_i)$와 이들의 finite intersection들의 fundamental groupoid가 모두 알려져 있다면 이들로부터 $\Pi_1(X)$의 fundamental groupoid를 계산할 수 있다는 것이다.

정리 13 (Seifert-van Kampen) 위상공간 $X$의 path-connected open cover $\mathcal{O}=(U_i)$가 주어졌다 하고, $\mathcal{O}$의 원소들의 유한한 교집합이 다시 $\mathcal{O}$에 속한다고 가정하자. 그럼 $\mathcal{O}$-shaped diagram $\Pi_1:\mathcal{O}\rightarrow\Grpd$의 colimit이 존재하며 이는 $\Pi_1(X)$와 isomorphic하다.

증명

즉 임의의 groupoid $\mathscr{G}\in\Grpd$와 임의의 cocone $\lambda:\Pi_1\vert_\mathcal{O}\Rightarrow \mathscr{G}$에 대하여, 각각의 $U\in \mathcal{O}$마다 $\widetilde{\lambda}$와 $\lambda$가 같아지도록 하는 $\widetilde{\lambda}$가 존재한다는 것을 보이면 된다. 당연히 우리는 임의의 $x\in X$마다, $x\in U$를 만족하는 $U$를 찾은 뒤 이 위에서는 $\lambda_U$가 정의되므로 $\widetilde{\lambda}(x)$를 이 값 $\lambda_U(x)$로 정의하면 된다. 이것이 $U$의 선택에 무관하다는 것은 $x$를 포함하는 임의의 $U_1,U_2$에 대해 $\lambda_{U_1}(x)$와 $\lambda_{U_2}(x)$는 모두 $\lambda_{U_1\cap U_2}(x)$와 같은 값을 가져야 한다는 것으로부터 자명하다. 한편 morphism에 대하여도 비슷한 식으로 정의를 할 수 있는데, 어떠한 $U\in \mathcal{O}$에 완전하게 포함되는 path $f$에 대해서는 위와 마찬가지 이유로 이 정의가 잘 정의되며, 유일하게 보여야 하는 것은 path가 단일한 $U\in \mathcal{O}$에 속해있지 않은 경우 어떻게 정의해야 할지에 대한 것이다. 그런데 이 경우 그냥 path의 concatenation을 사융하면 된다. 이것이 항상 정의되며 잘 정의된다는 것을 보이면 된다.

이제 위의 따름정리 12를 얻어낼 때와 마찬가지로 하나의 대상에서만 이 정리를 적용하고, 따라서 $\Grpd$를 $\Grp$로 바꿔준 후, $\Grp$의 colimit이 free product임을 사용하면 다음의 결과를 얻는다.

따름정리 14 (Seifert-van Kampen theorem, classical version) 위상공간 $X$가 두 connected open subset $U,V$의 합집합으로 나타난다고 하고, $U\cap V$가 connected라 하자. 그럼 다음의 diagram

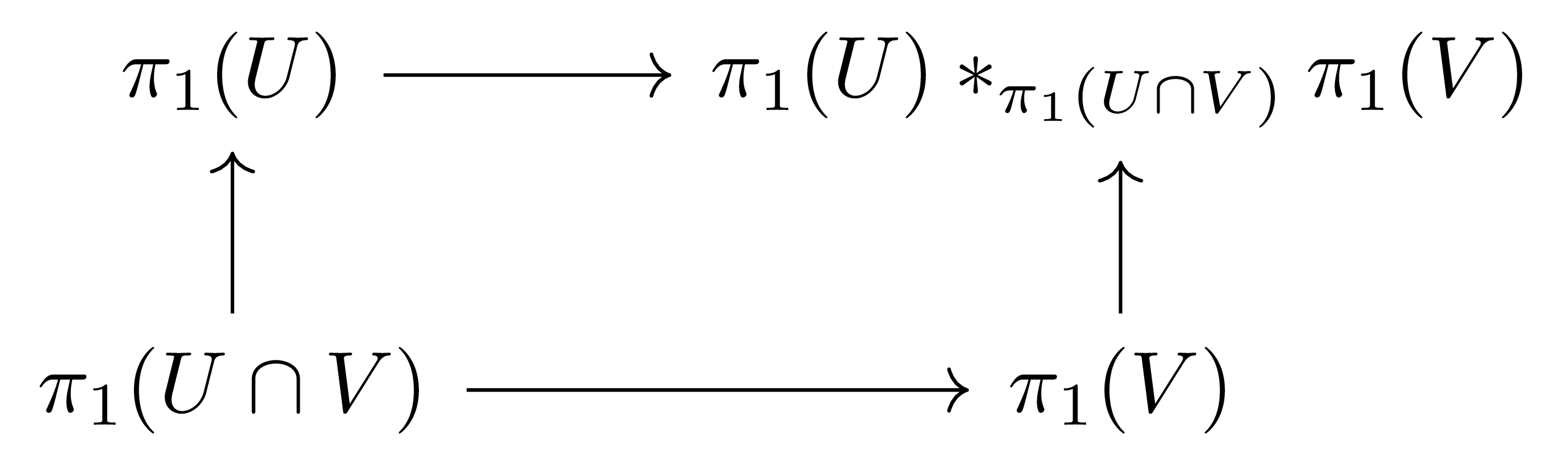
$van_Kampen$

이 pushout diagram이며 이로부터 나오는 $\pi_1(U)\ast_{\pi_1(U\cap V)}\pi_1(V)\rightarrow \pi_1(X)$는 isomorphism이다.

Hurewicz theorem

Homology group은 fundamental group보다 더 단순한 구조를 가지고 있다. 가령 $\pi_1(X)$는 일반적으로 abelian group일 필요가 없지만, $H_1(X)$는 그 정의에 의해 abelian group이다. 그러나 §호몰로지, ⁋예시 8에서 살펴본 것처럼 $H_1(X)$의 원소들도 일단은 일종의 loop들처럼 생각할 수 있으므로 이들 사이의 관계를 기대하는 것이 자연스럽다.

정리 15 (Hurewicz) Path-connected space $X$를 고정하자. 그럼 각각의 $n$에 대하여, group homomorphism

\[h_n:\pi_n(X) \rightarrow H_n(X)\]

이 존재한다. 특별히 $n=1$인 경우, $h_1$은 surjective이고 $\ker h_1$은 $\pi_1(X)$의 commutator subgroup $[\pi_1(X),\pi_1(X)]$이 되어 first isomorphism theorem에 의해

\[H_1(X)\cong \pi_1(X)/\ker h_1=\pi_1(X)/[\pi_1(X),\pi_1(X)]=\pi_1(X)^\ab\]

이 성립한다. 더 일반적으로, 만일 모든 $i< n$에 대하여 $\pi_i(X)=0$이라면 $h_n$은 isomorphism이고 $h_{n+1}$은 surjective이다.

Hurewicz homomorphism $h_n$은 임의의 $f:S^n \rightarrow X$가 주어졌을 때 $f_\ast([S^n])$으로 주어진다. 여기에서 $[S^n]$은 $H_n(S^n)\cong \mathbb{Z}$의 generator이다.

참고문헌

[Hat] A. Hatcher, Algebraic Topology. Cambridge University Press, 2022.
[May] J. P. May, A concise course in algebraic topology.
[Mun] James Munkres, Topology. Prentice Hall, 2000.
[Tao] Terence Tao, van Kampen’s theorem via covering spaces.

Twitter Facebook LinkedIn

피복공간

K

피복공간

피복공간의 기본정리

자이페르트-반 캄펜 정리

Hurewicz theorem

공유하기

댓글남기기