코호몰로지

코호몰로지는, 그 이름에서 알 수 있듯, 호몰로지의 dual에 해당하는 개념이라 할 수 있다. 그러나 단순히 공간 \(X\)의 \(k\)번째 코호몰로지 \(H^k(X)\)가 \(k\)번째 호몰로지 \(H_k(X)\)의 dual이었다면 이를 별도로 생각할 필요가 없을 것이다.

실제로 코호몰로지는 호몰로지보다 더 정교한 불변량을 주는데, 가령 코호몰로지 위에는 자연스러운 곱셈 구조가 정의되며, 같은 호몰로지를 갖는 공간이라 하더라도 이 곱셈구조가 다르다면 homtopic하지 않다. 이번 글에서는 코호몰로지의 정의와 기본적인 성질들에 대해 살펴본다.

호몰로지의 보편계수정리

본격적인 논의를 시작하기 전에 우리는 §호몰로지의 계산, ⁋정의 6 이후에 다루었던 homology with coefficient에 대해 우선 살펴본다. 우리는 simplicial homology 혹은 singular homology를 정의할 때 chain group들 \(C_\bullet(X)\) 혹은 \(C_\bullet^\Delta(X)\) 대신 abelian group \(A\)와의 tensor product를 통하여 chain complex

\[C_\bullet(X;A):=C_\bullet(X)\otimes_\mathbb{Z}A,\qquad C_\bullet^\Delta(X;A):=C_\bullet^\Delta(X)\otimes_\mathbb{Z}A\]

을 얻어내고, 그럼 이들의 homology group들로 호몰로지들

\[H_k(X;A),\qquad H_k^\Delta(X;A)\]

을 정의할 수 있다는 것을 살펴보았다. 이를 실질적으로 계산하기 위해서는 가령 \(H_k(X;A)\) 혹은 \(H_k^\Delta(X;A)\)가 \(H_k(X;A)\otimes_\mathbb{Z}A\) 혹은 \(H_k^\Delta(X;A)\otimes_\mathbb{Z}A\)와 같은 식으로 나오는지를 추가적으로 살펴보아야 할 것인데, 일반적으로 텐서곱은 right-exact이지만 left-exact는 아니므로 이는 과도한 기대일 것이며, 우리는 텐서를 취함으로써 손실되는 정보를 추가로 측정해주어야 할 것이다.

이를 위해, free abelian group들로 이루어진 chain complex \(C_\bullet\)을 생각하고, \(\Ch_{\geq 0}(\Ab)\)에서의 short exact sequence

\[0 \rightarrow Z_\bullet \rightarrow C_\bullet \rightarrow B_{\bullet-1}\rightarrow 0\tag{1}\]

를 생각하자. 여기에서 \(Z_k=\ker(\partial:C_k \rightarrow C_{k-1})\)이며 \(B_{k-1}=\im(\partial:C_k \rightarrow C_{k-1})\)이고 위의 sequence의 첫째 함수는 inclusion, 둘째 함수는 boundary map \(\partial\)이다.

이 때, \(Z_{k}\)과 \(B_{k-1}\)은 각각 free abelian group \(C_k,C_{k-1}\)의 subgroup이므로 free이고, 따라서 ##ref##에 의해 이 short exact sequence는 split exact sequence이며 따라서 임의의 abelian group \(A\)에 대하여, 다음의 sequence

\[0 \rightarrow Z_\bullet\otimes_\mathbb{Z}A \rightarrow C_\bullet\otimes_\mathbb{Z}A \rightarrow B_{\bullet-1}\otimes_\mathbb{Z}A\rightarrow 0\]

또한 spiltting short exact sequence이다. (##ref) 이 때, 이들을 풀어쓰면 다음의 commutative diagram

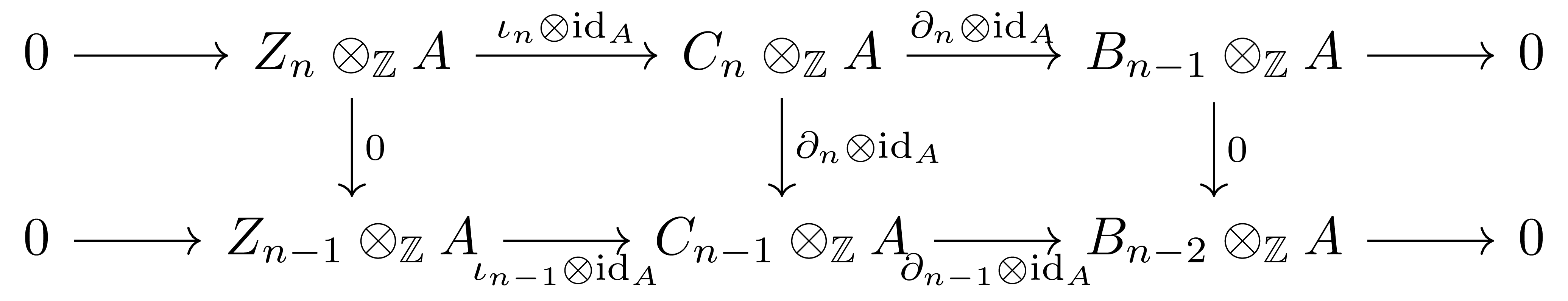
과 같은 꼴이고 따라서 [호몰로지 대수학] §긴 완전열, ⁋정리 1에 의해 다음의 long exact sequence

\[\cdots B_k\otimes_\mathbb{Z}A\overset{\delta_k}{\longrightarrow}Z_k\otimes_\mathbb{Z}A\rightarrow H_k(C\otimes A)\rightarrow B_{k-1}\otimes_\mathbb{Z}A\overset{\delta_{k-1}}{\longrightarrow} Z_{k-1}\otimes_\mathbb{Z}A\rightarrow\cdots\tag{2}\]

를 얻는다.

이제 이 exact sequence로부터 정보를 얻어내기 위해서는 connecting map \(\delta\)들을 살펴보아야 한다. 정의를 따라가보면, \(\delta_k:B_k\otimes_\mathbb{Z}A\rightarrow Z_k\otimes_\mathbb{Z}A\)는 정확하게 inclusion homomorphism \(i_k:B_k \rightarrow Z_k\)에 \(-\otimes \id_A\)를 취한 것과 같으므로, 다음의 short exact sequence

\[0 \rightarrow B_k\overset{i_k}{\longrightarrow} Z_k \overset{p_k}{\longrightarrow}H_k(C)\rightarrow 0\]

을 생각하자. 그럼, \(B_k\)과 \(Z_k\), 그리고 \(0\)은 모두 free abelian group이므로 이는 \(H_k(C_\bullet)\)의 free resolution으로 볼 수 있고, 따라서 정의에 의해 \(\delta_k\)을 다음의 exact sequence

\[0 \rightarrow \Tor_1^\mathbb{Z}(H_k(C))\rightarrow B_k\otimes_\mathbb{Z}A\overset{\delta_k}{\longrightarrow} Z_k\otimes_\mathbb{Z}A\rightarrow H_k\otimes_\mathbb{Z}A\rightarrow 0\]

에 넣을 수 있다. 즉, 다음의 isomorphism

\[\ker\delta_{k-1}\cong \Tor_1^\mathbb{Z}(H_{k-1}(C), A),\qquad \coker\delta_k\cong H_k(C)\otimes_\mathbb{Z} A\]

이 존재하며, 이를 (2)에 대입하면 short exact sequence

\[0 \rightarrow H_k(C)\otimes_\mathbb{Z}A\rightarrow H_k(C;A)\rightarrow \Tor_1^\mathbb{Z}(H_{k-1}(C), A)\rightarrow 0\]

을 얻는다.

한편 (1)은 splitting short exact sequence이므로, 우리는 retraction \(r_k:C_k \rightarrow Z_k\)을 하나 택할 수 있다. ([다중선형대수학] §완전열, ⁋명제 10) 그럼 이러한 선택 하에서, \((p_k\circ r_k)\otimes \id_A\)는 호몰로지에서의 함수 \(H_k(C;A)\rightarrow H_k(C)\otimes_\mathbb{Z} A\)를 유도하며 이것이 위의 \(H_k(C)\otimes_\mathbb{Z}A\rightarrow H_k(C;A)\)의 retraction임을 안다. 즉 다음을 얻는다.

명제 1 (Universal coefficient theorem for homology) 임의의 위상공간 \(X\)와 abelian group \(A\)에 대하여, 다음의 short exact sequence

\[0 \rightarrow H_k(X)\otimes_\mathbb{Z}A\rightarrow H_k(X;A)\rightarrow \Tor_1^\mathbb{Z}(H_{k-1}(X), A)\rightarrow 0\]

가 존재한다. 뿐만 아니라, 이 sequence는 (non-canonical하게) split하며 따라서 다음의 (non-canonical) isomorphism

\[H_k(X;A)\cong \left(H_k(X)\otimes_\mathbb{Z}A\right)\oplus \Tor_1^\mathbb{Z}(H_{k-1}(X), A)\]

을 준다.

코호몰로지의 정의와 보편계수정리

§호몰로지의 계산, ⁋정의 6과 마찬가지로 우리는 코호몰로지의 Eilenberg-Steenrod axiom을 정의하고, 이를 만족하는 contravariant functor와 connecting morphism들을 cohomology라 부를 수 있을 것이다. 이를 명시적으로 적으면 다음과 같다.

정의 2 (Eilenberg-Steenrod axioms) 위상공간들의 pair들의 category에서 abelian group들의 category로의 contravariant functor들 \(H^k\)과, 이들 사이의 natural transformation

\[\delta: H^k(X) \rightarrow H^{k+1}(X,A)\]

들에 대하여, Eilenberg-Steenrod axiom은 다음의 공리들을 뜻한다.

• (Homotopy) 두 homotopic map \((X,A) \rightarrow (Y,B)\)이 주어졌다면, 이들이 유도하는 두 homomorphism들 \(H^k(Y,B) \rightarrow H^k(X,A)\)들도 동일하다.
• (Excision) §호몰로지의 계산, ⁋정리 2의 조건을 만족하는 \((X,A,Z)\)에 대하여, \((X\setminus Z, A\setminus Z)\hookrightarrow (X,A)\)는 isomorphism을 유도한다.
• (Dimension) One-point space \(\ast\)에 대하여, \(H^k(\ast)=0\)이 모든 \(k>0\)에 대해 성립한다.
• (Additivity) 만일 \(X=\coprod X_\alpha\)라면, \(H^k(X)\cong\bigoplus H^k(X_\alpha)\)이다.

• (Exactness) 각각의 pair \((X,A)\)와, 두 inclusion \((A,\emptyset) \hookrightarrow (X,\emptyset)\) 그리고 \((X,\emptyset)\hookrightarrow (X,A)\)들은 다음의 long exact sequence

  \[\cdots \rightarrow H^k(X,A)\rightarrow H^k(X) \rightarrow H^k(A) \rightarrow H^{k+1}(X,A)\rightarrow \cdots\]

  에 들어간다.

이러한 조건들을 만족하는 cohomology theory의 존재성을 보이기 위해 §호몰로지에서와 마찬가지로 위상공간 \(X\)의 singular simplex들로 이루어진 chain complex

\[C_\bullet(X):\qquad\cdots \rightarrow C_{k+1}(X)\rightarrow C_k(X) \rightarrow C_{k-1}(X)\rightarrow \cdots\]

를 생각하자. Coefficient group으로 사용할 abelian group \(A\)를 하나 고정하면, 이 chain complex의 dual에 해당하는 다음의 chain complex

\[(C^\vee)^\bullet(X;A):\qquad\cdots \leftarrow \Hom_\mathbb{Z}(C_{k+1}(X), A)\leftarrow\Hom_\mathbb{Z}(C_k(X),A)\leftarrow\Hom_\mathbb{Z}(C_{k-1}(X),A)\leftarrow\cdots\]

를 생각할 수 있다. 이는 [대수적 구조] §가군의 직접곱과 직합, 텐서곱, ⁋정리 6에 의하여

\[\qquad \cdots\leftarrow\Hom_A(C_{k+1}(X;A),A)\leftarrow \Hom_A(C_k(X;A),A)\leftarrow \Hom_A(C_{k-1}(X;A),A)\leftarrow\cdots\]

으로 생각할 수 있으므로, chain complex \(C_\bullet(X;A)\)의 dual에 해당하는 것이라 생각할 수 있다. 그럼 이 chain complex \((C^\vee)^\bullet(X;A)\)의 \(k\)번째 호몰로지를

\[H^k(X;A):=H_k(C^\vee)\]

로 적고, 이를 \(X\)의 \(k\)번째 코호몰로지라 부른다. 여기서 \(H\)와 \(C^\vee\)에 위첨자를 이용하여 index를 표기해주는 이유는 homology와 반대로, long exact sequence가 index가 커지는 방향으로 만들어지기 때문이며, 앞으로는 혼동의 여지가 없다면 \((C^\vee)^\bullet(X)\)를 \(C^\bullet(X;A)\)라 쓰기로 하자.

그럼 이렇게 정의한 \(H^k(X;A)\)와 \(H_k(X)\) 사이에 어떠한 관계가 있는지를 살펴보아야 한다. 이 글의 서두에서 밝힌 것과 같이, 단순히 \(H^k(X;A)\cong H_k(X)^\ast\)가 성립하는 것은 아니다. 그러나 위의 명제 1의 증명과 유사한 방식으로 우리는 다음의 명제를 얻어낼 수 있다.

명제 3 (Universal coefficient theorem for cohomology) 임의의 위상공간 \(X\)와 abelian group \(A\)에 대하여, 다음의 short exact sequence

\[0\rightarrow\Ext_\mathbb{Z}^1(H_{k-1}(X), A)\rightarrow H^k(X;A)\rightarrow \Hom_\mathbb{Z}(H_k(X),A)\rightarrow 0\]

이 존재한다. 뿐만 아니라, 이 sequence는 (non-canonical하게) split하며 따라서 다음의 (non-canonical) isomorphism

\[H^k(X;A)\cong \Hom_\mathbb{Z}(H_k(X),A)\oplus \Ext^1_\mathbb{Z}(H_{k-1}(X),A)\]

을 준다.

이는 대략적으로, 명제 1을 [대수적 구조] §가환군, ⁋정리 15를 통해 번역한 것이라 생각할 수 있다.

드람 코호몰로지

위상공간 \(X\)에 chain complex \(C_\bullet(X)\)를 대응시키는 것은 \(X\)의 부분공간들에 대한 정보를 대수적으로 옮기는 것이라 할 수 있다. 코호몰로지를 정의할 때 우리는 \(C_\bullet(X)\)에 \(\Hom_\mathbb{Z}(-,A)\)를 취한 후 이 cochain complex의 호몰로지를 정의하며, 이 때

\[C^k(X;A)=\Hom_\mathbb{Z}(C_k(X), A)\]

의 임의의 원소는 \(C_k(X)\)의 원소들 (즉 \(k\)-chain들)마다 \(A\)의 원소를 대응시키는 함수로 생각할 수 있다. 즉 코호몰로지는 본질적으로 공간 위에 정의된 함수들을 보는 것이라 할 수 있다.

더 구체적으로, 임의의 \(c\in C_k(X)\)와 \(\varphi\in C^k(X;A)\)에 대하여 우리는 다음의 canonical pairing

\[C_k(X)\times C^k(X;A)\rightarrow A;\qquad (c,\varphi)\mapsto \varphi(c)\in A\]

이 존재한다는 것을 알고, 이 때 \(C_\bullet(X)\)의 boundary map을 \(\partial\), 이로부터 나오는 \(C^\bullet(X;A)\)의 coboundary map을 \(\delta\)라 한다면 임의의 \(c\in C_{k+1}(X)\)와 \(\varphi\in C^k(X;A)\)에 대하여 다음의 식

\[\langle \partial c, \varphi\rangle=\langle c, \delta\varphi\rangle\]

이 성립하는 것을 알고, 이로부터 이들이 homology와 cohomology 레벨의 pairing

\[H_k(X)\times H^k(X;A)\rightarrow A\]

을 주는 것을 안다.¹

예를 들어 de Rham cohomology를 보기 위해 differential \(k\)-form들로 이루어진 \(\mathbb{R}\)-벡터공간들

\[\Omega^k(\mathbb{R}^n)=\{\text{$k$-forms on $\mathbb{R}^n$}\}\]

를 생각하자. 여기서 coboundary map \(\Omega^k(\mathbb{R}^n)\rightarrow \Omega^{k+1}(\mathbb{R}^n)\)은 exterior derivative로 주어지며, differential \(k\)-form은 \(k\)차원 부분집합이 주어졌을 때, 적분을 통해 이에 대응하는 숫자를 내놓는다. 또, closed \(k\)-form들은 이 coboundary의 kernel로, exact \(k\)-form들은 이 coboundary의 image로 주어진다.

가령 \(\mathbb{R}^3\) 위에 정의된 differential \(2\)-form

\[\omega=dx\wedge dy\]

을 생각하자. \(\mathbb{R}^3\)의 \(2\)차원 부분집합은 \(\mathbb{R}^2\)의 (단위) 직사각형에서 \(\mathbb{R}^3\)으로의 함수로 주어지며, 이를 통해 우리는 \(2\)차원 부분집합에 \(\omega\)를 적용하는 것이 무엇인지 안다.

가령 다음의 집합

\[S = \{ (x, y, 0) \mid 0 \leq x \leq 1,\, 0 \leq y \leq 1 \}\]

이 주어졌다 하자. 그럼 이 집합에서의 \(\omega\)의 값은 단순히

\[\int_S \omega = \int_{x=0}^{1} \int_{y=0}^{1} 1\,dy\,dx = 1\]

로 계산된다. 다른 예시로, 곡면

\[\Sigma = \{ (x, y, z) \mid x^2 + y^2 + z^2 = 1,\ z \geq 0 \}\]

이 주어졌다면, 우리는 우선 구면좌표계

\[x = \sin \phi \cos \theta,\qquad y = \sin \phi \sin \theta,\qquad z = \cos \phi\]

를 이용하여 이를 \([0,\pi/2]\times[0,2\pi]\)에서 \(\Sigma\)의 함수로 매개화한 후, \(dx \wedge dy = \sin \phi \cos \phi\, d\phi \wedge d\theta\)임을 이용하여

\[\begin{align*} \int_{\Sigma} \omega &= \int_{0}^{2\pi} \int_{0}^{\pi/2} \sin \phi \cos \phi\, d\phi \, d\theta = \int_{0}^{2\pi} d\theta \int_{0}^{\pi/2} \sin \phi \cos \phi\, d\phi \\ &= 2\pi \times \frac{1}{2} \int_{0}^{\pi/2} \sin(2\phi) d\phi = 2\pi \times \frac{1}{2} \left[ -\frac{1}{2} \cos(2\phi) \right]_{0}^{\pi/2} \\ &= 2\pi \times \frac{1}{2} \left( -\frac{1}{2} [\cos(\pi) - \cos(0)] \right) = 2\pi \times \frac{1}{2} \left( -\frac{1}{2}(-1 - 1) \right) = 2\pi \times \frac{1}{2} \times 1 \\ &= \pi \end{align*}\]

와 같은 식으로 적분을 계산할 수 있다. 그럼 differential \(2\)-form \(\omega\)는, 이러한 방식으로 \(S\)나 \(\Sigma\)와 같은 2차원 부분집합을 받아 숫자를 내놓는 함수라 생각할 수 있다.

이제 Poincaré lemma에 의하여 우리는 \(\mathbb{R}^n\) 위의 임의의 closed \(k\)-form들은 항상 적당한 \(k-1\)-form의 exterior derivative로 나온다는 것을 안다. 따라서 임의의 \(k>0\)에 대하여

\[H^k_\dR(\mathbb{R}^n)=0\]

이며, \(k=0\)인 경우, 미분했을 때 \(0\)이 되는 함수는 정확히 상수함수이므로

\[H^0_\dR(\mathbb{R}^n)=\mathbb{R}\]

이다.

이러한 방식으로 정의된 de Rham cohomology 또한 정의 2의 모든 조건들을 만족하며, 따라서 cohomology theory의 유일성 (그리고 임의의 singular chain을 smooth chain으로 근사할 수 있다는 사실)에 의해 \(\mathbb{R}\) 계수의 singular cohomology와 de Rham cohomology가 같다는 것을 확인할 수 있다. 위의 계산은 그럼 §호몰로지, ⁋명제 11의 계산을 명제 3을 통해 \(\mathbb{R}\)-valued cohomology로 옮겨온 것에 불과하다.

(코)호몰로지의 계수

위에서 살펴본 de Rham cohomology는 coefficient group이 \(\mathbb{Z}\)가 아닌 cohomology theory의 한 예시이다. Singular cohomology 혹은 simplicial cohomology theory와는 다르게, de Rham cohomology는 coefficient group이 \(\mathbb{R}\)인 것이 그 정의상 당연하다.

이러한 cohomology theory는 좋은 성질들을 가지고 있는데, 가령 \(\mathbb{R}\)은 torsion-free abelian group이므로 \(\Tor_1^\mathbb{Z}(A,\mathbb{R})=0\)이 임의의 abelian group \(A\)에 대해 성립하고, 따라서 명제 1에 의해 다음의 isomorphism

\[H_k(X;\mathbb{R})\cong H_k(X)\otimes_\mathbb{Z}\mathbb{R}\]

이 성립한다는 것을 안다. 뿐만 아니라, \(\mathbb{R}\)은 injective \(\mathbb{Z}\)-module이므로 \(\Ext_\mathbb{Z}^1(A,\mathbb{R})=0\)이 임의의 abelian group \(A\)에 대해 성립하고 따라서 이번에는 명제 3이 다음의 isomorphism

\[H^k(X;\mathbb{R})\cong \Hom_\mathbb{Z}(H_k(X),\mathbb{R})\]

을 준다.

그럼 이러한 종류의 호몰로지와 코호몰로지를 살펴보는 것이 또 다른 관심사가 될 것이다. 이를 위해 \(H_k(X;A)\)와 \(H^k(X;A)\)를 정의할 때 사용했던 chain complex를 다시 떠올려보면, 우리는 두 chain complex

\[C_\bullet(X;A):=C_\bullet(X)\otimes_\mathbb{Z}A,\qquad C_\bullet^\Delta(X;A):=C_\bullet^\Delta(X)\otimes_\mathbb{Z}A\]

들은, 만일 \(A\)가 ring이었다면, \(A\)-module들의 chain complex이고, 앞서 정의한 \(C^\bullet(X;A)\) 또한 그러하다는 것을 안다.따라서 이들에 호몰로지 혹은 코호몰로지를 취하면 그 결과 또한 \(A\)-module이 될 것이다.

한편, 우리는 만일 \(A\)가 principal ideal domain이라면 임의의 free \(A\)-module의 submodule은 다시 free \(A\)-module임을 알고 있다. 명제 1의 증명을 다시 살펴보면, \(\mathbb{Z}\)가 principal ideal domain이므로 free \(\mathbb{Z}\)-module (즉 free abelian group)의 submodule이 다시 free \(\mathbb{Z}\)-module이 된다는 사실을 활용한 것이며, 이를 바탕으로 앞선 두 명제를 다음과 같이 일반화할 수 있다.

정리 4 (Universal coefficient theorem for homology, general version) Principal ideal domain \(A\)와, free \(A\)-module들의 chain complex \(C_\bullet\), 그리고 임의의 \(A\)-module \(M\)에 대하여 다음의 short exact sequence

\[0 \rightarrow H_k(C)\otimes_AM\rightarrow H_k(C\otimes_AM)\rightarrow \Tor_1^A(H_{k-1}(C), A)\rightarrow 0\]

이 존재한다. 뿐만 아니라, 이 sequence는 (non-canonical하게) split하며 따라서 다음의 (non-canonical) isomorphism

\[H_k(C\otimes_AM)\cong \left(H_k(C)\otimes_AM\right)\oplus \Tor_1^A(H_{k-1}(C), M)\]

을 준다.

정리 5 (Universal coefficient theorem for cohomology, general version) Principal ideal domain \(A\)와, free \(A\)-module들의 chain complex \(C_\bullet\), 그리고 임의의 \(A\)-module \(M\)에 대하여 다음의 short exact sequence

\[0\rightarrow\Ext_A^1(H_{k-1}(C), M)\rightarrow H_k(\Hom_A(C,M))\rightarrow \Hom_A(H_k(C),M)\rightarrow 0\]

이 존재한다. 뿐만 아니라, 이 sequence는 (non-canonical하게) split하며 따라서 다음의 (non-canonical) isomorphism

\[H_k(\Hom_A(C,M))\cong \Hom_A(H_k(C),M)\oplus \Ext^1_A(H_{k-1}(C),M)\]

을 준다.

메이어-피토리스 열

한편 정의 2의 공리들 중 excision axiom은 우리가 작은 공간들의 코호몰로지로부터 큰 공간의 코호몰로지를 계산할 수 있게 해 준다. 다음 명제는 [대수적 위상수학] §호몰로지의 계산, ⁋명제 7의 코호몰로지 버전이며, 그 증명은 [대수적 위상수학] §호몰로지의 계산, ⁋정의 6로부터 [대수적 위상수학] §호몰로지의 계산, ⁋명제 7를 얻어낸 과정을, 정의 2에서 시작하여 반복하면 된다.

명제 6 (Mayer-Vietoris sequence) 위상공간 \(X\)가 두 열린집합들의 합집합 \(X=U\cap V\)로 나타난다 하고, 이 위에 정의된 cohomology theory \(H\)를 생각하자. 그럼 long exact sequence

\[\cdots \to H^{n}(X) \xrightarrow{(i^*, j^*)} H^{n}(U) \oplus H^{n}(V) \xrightarrow{k^* - l^*} H^{n}(U \cap V) \xrightarrow{\delta} H^{n+1}(X) \to \cdots\]

가 존재하며, 이 때 \(i^\ast, j^\ast, k^\ast, l^\ast\)는 각각 inclusion들

\[i:U\rightarrow X,\quad j:V\rightarrow X,\quad k:U\cap V\rightarrow U,\quad l:U\cap V \rightarrow V\]

에 유도되는 함수들이다.

사슬복합체의 텐서곱

Mayer-Vietoris sequence를 사용하면 큰 공간의 작은 부분공간들의 호몰로지 혹은 코호몰로지로부터 큰 공간의 호몰로지, 코호몰로지를 계산할 수 있다. 한편 우리는 두 공간 \(X,Y\)를 곱하여 더 큰 공간 \(X\times Y\)를 만들 수도 있는데, 퀴네트 공식은 이러한 곱공간의 호몰로지와 코호몰로지를 계산하는 데에 도움을 준다. 이를 위해서는 우선 두 chain complex \(C_\bullet\), \(D_\bullet\)이 주어졌을 때 이들의 텐서곱을 정의해야 한다.

정의 7 Ring \(A\)와 \(A\)-module들의 chain complex \(C_\bullet,D_\bullet\)이 주어졌다 하자. 그럼 이들의 tensor product \((C\otimes D)_\bullet\)은 각각의 \(k\)에 대하여

\[(C\otimes D)_k=\bigoplus_{p+q=k}C_p\otimes_A D_q\]

로 정의하고, differential은 homogeneous element에 대해서는

\[\partial(x,y)=(\partial^Cx,y)+(-1)^{\deg(x)}(x,\partial^Dy)\]

으로 정의한 후, 이를 linear하게 확장하여 얻어지는 것이다.

즉, \((C\otimes D)_\bullet\)은 \((p,q)\) 성분이 \(C_p\otimes D_q\)이고, horizontal differential이 \(\partial^C\otimes\id_D\), vertical differential이 \(\id_C\otimes \partial^D\)로 주어지는 double complex의 total complex라 할 수 있다. (##ref##)

그럼 퀴네트 공식의 대수적인 내용은 다음 보조정리에 담겨있다.

보조정리 8 Principal ideal doamin \(A\)와 \(A\)-module들의 chain complex \(C_\bullet\), \(D_\bullet\)이 주어졌다 하고 \(C_\bullet\)이 free \(A\)-module들의 chain complex라 하자. 그럼 임의의 \(k\)에 대하여 다음의 short exact sequence

\[0 \rightarrow \bigoplus_{p+q=k}H_p(C)\otimes_AH_q(D)\rightarrow H_k(C\otimes D)\rightarrow \bigoplus_{p+q=k-1}\Tor_1^A(H_p(C),H_q(D))\rightarrow 0\]

가 존재한다. 뿐만 아니라, 이 short exact sequence는 (non-canonical하게) split하며 따라서 다음의 isomorphism

\[H_k(C\otimes D)\cong \left( \bigoplus_{p+q=k}H_p(C)\otimes_AH_q(D)\right)\oplus \left(\bigoplus_{p+q=k-1}\Tor_1^A(H_p(C),H_q(D)) \right)\]

이 존재한다.

증명

우선 다음의 short exact sequence

\[0 \rightarrow Z_p(C) \rightarrow C_p\rightarrow B_{p-1}(C)\rightarrow 0\]

를 생각하면, \(B_{p-1}(C)\)와 \(Z_p(C)\)는 free \(A\)-module \(C_{p-1},C_p\)의 submodule이고 \(A\)가 principal ideal domain이므로 이들은 다시 free \(A\)-module이다. 따라서 이 short exact sequence에 \(D_q\)를 텐서곱하여 얻어지는 다음의 short exact sequence

\[0\rightarrow Z_p(C)\otimes D_q \rightarrow C_p\otimes D_q \rightarrow B_{p-1}(C)\otimes D_q\rightarrow 0\]

이 존재한다. Chain complex \((C\otimes D)_\bullet\)의 정의로부터, \(p+q=k\)를 만족하는 모든 \((p,q)\)에 대해 이러한 short exact sequence를 생각한 후 모두 direct sum을 취하면 다음의 short exact sequence

\[0 \rightarrow (Z(C)\otimes D)_k \rightarrow (C\otimes D)_k \rightarrow (B(C)\otimes D)_{k-1}\rightarrow 0\]

를 얻는다. 이제 이 short exact sequence로부터 homology들의 long exact sequence를 생각하면,

\[\cdots \rightarrow H_{k}(B(C)\otimes D)\overset{\delta_k}{\longrightarrow} H_{k}(Z(C)\otimes D)\rightarrow H_{k}(C\otimes D)\rightarrow H_{k-1}(B(C)\otimes D)\overset{\delta_{k-1}}{\longrightarrow} H_{k-1}(Z(C)\otimes D)\rightarrow \cdots\]

를 얻을 수 있다. 특히 \(H_k(C\otimes D)\)를 기준으로 다음의 short exact sequence

\[0 \rightarrow \coker\delta_k\rightarrow H_k(C\otimes D)\rightarrow \ker\delta_{k-1}\rightarrow 0 \tag{$\ast$}\]

를 얻는다. 이제 \(\coker\delta_k\)와 \(\ker\delta_{k-1}\)을 살펴보기 위해 short exact sequence

\[0 \rightarrow B_\bullet(C)\rightarrow Z_\bullet(C)\rightarrow H_\bullet(C)\rightarrow 0\]

를 생각하고, 여기에 \(H_\bullet(D)\)와의 tensor product로 얻어지는 다음의 exact sequence

\[0 \rightarrow \Tor_1^A(H(C), H(D))_\bullet\rightarrow (B(C)\otimes H(D))_\bullet\rightarrow (Z(C) \otimes H(D))_\bullet \rightarrow (H(C)\otimes H(D))_\bullet \rightarrow 0\]

를 생각하자. 여기서 첫 항의 \(0\)은 \(Z_\bullet(C)\)이 free module들인 것으로부터 얻어진 것이다. 한편, free module은 flat이므로, free module과의 tensor product를 취하는 것은 호몰로지를 취하는 것과 commute하고 따라서 위의 sequence에서

\[(B(C)\otimes H(D))_\bullet\cong H_\bullet(B(C)\otimes D)\qquad (Z(C)\otimes H(D))_\bullet \cong H_\bullet(Z(C)\otimes D)\]

임을 안다. 이 때 \((B(C)\otimes H(D))_\bullet \rightarrow (Z(C)\otimes H(D))_\bullet\)은 inclusion \(B_\bullet(C)\rightarrow Z_\bullet(C)\)으로부터 얻어지는 것이며, 위의 identification을 거쳤을 때 \(\delta_\bullet\)과 같은 함수인 것을 안다. 따라서

\[\coker \delta_k\cong (H(C)\otimes H(D))_k,\qquad \ker \delta_{k-1}\cong \Tor_1^A(H(C),H(D))_{k-1}\]

을 얻는다. Splitting에 대한 주장의 경우,

\[0 \rightarrow Z_\bullet(C)\rightarrow C_\bullet \rightarrow B_{\bullet-1}(C) \rightarrow 0\]

이 split exact sequence이므로, section \(B_{\bullet-1}(C)\rightarrow C_\bullet\)에 의해 (\(\ast\))의 splitting이 유도된다.

아일렌베르크-질버 정리와 퀴네트 공식

보조정리 8의 결과를 염두에 두면, 우리가 해야 할 일은 명확하다. 두 위상공간 \(X,Y\)와 이에 해당하는 chain complex \(C_\bullet(X),C_\bullet(Y)\)가 주어졌을 때, product space \(X\times Y\)의 호몰로지 \(H_\bullet(X\times Y)\)와, 두 chain complex \(H_\bullet(X)\), \(H_\bullet(Y)\)의 tensor product \((H(X)\otimes H(Y))_\bullet\)의 관계를 살펴보는 것이다. 다음 정리는 이를 두 대수적인 대상들이 동일한 것이라는 것을 보여준다.

정리 9 (Eilenberg-Zilber) 두 위상공간 \(X,Y\)와 이들로부터 얻어지는 chain complex \(C_\bullet(X),C_\bullet(Y)\), 그리고 \(C_\bullet(X\times Y)\)에 대하여, 두 chain complex \((C(X)\otimes C(Y))_\bullet\)과 \(C_\bullet(X\times Y)\) 사이의 chain homotopy equivalence가 존재하며, 따라서

\[H_\bullet(C(X\times Y))\cong H_\bullet(C(X)\otimes C(Y))\]

이 성립한다.

이는 보편적으로 acyclic models theorem을 사용하여 증명하지만, acyclic models theorem은 사실 Eilenberg-Zilber theorem의 일반화에 가까운 정리라 acyclic models theorem을 사용하여 이를 증명하는 것은 과한 감이 있다. 다만 Eilenberg-Zilber theorem을 직접 증명하는 것은 상당히 피곤한 일이므로, 우리는 이 증명 과정에서 등장하는 두 map

\[\AW:C_\bullet(X\times Y) \rightarrow (C(X)\otimes C(Y))_\bullet,\qquad \EZ:(C(X)\otimes C(Y))_\bullet \rightarrow C_\bullet(X\times Y)\]

만 살펴볼 것이다. Acyclic models theorem에 대한 증명은 흐름을 깨지 않기 위해 별도의 글로 적어둔다.

우선 Alexander-Whitney map \(\AW:C_\bullet(X\times Y) \rightarrow (C(X)\otimes C(Y))_\bullet\)의 경우, 임의의 \(k\)-simplex \(\sigma:\Delta^k \rightarrow X\times Y\)를

\[\sum_p (\pi_X\circ \sigma\vert_{[v_0,\ldots,v_p]})\otimes (\pi_Y\circ \sigma\vert_{[v_p,\ldots v_k]})\in \bigoplus_{p+q=k}C_p(X)\otimes C_q(Y)\]

으로 보내어 얻어진다. 이는 만일 \(X=Y\)였다면, \(C(X)\rightarrow C(X)\otimes C(X)\)를 통해 \(C(X)\)를 (differential graded counital coassociative) coalgebra로 만드는 함수가 될 것이며 이러한 이유로 다음 글에서 다시 등장하게 된다.

Eilenberg-Zilber map \(\EZ:(C(X)\otimes C(Y))_\bullet \rightarrow C_\bullet(X\times Y)\)는 simple tensor들에 대하여 다음의 식

\[\EZ(\sigma\otimes\tau)=\sum_{\substack{\alpha_1<\cdots <\alpha_p\\\beta_1<\cdots <\beta_q}}\sgn(\alpha_1,\ldots,\alpha_p,\beta_1,\ldots,\beta_q)(\sigma\circ s_{\alpha_p}\cdots s_{\alpha_1})\times(\tau\circ s_{\beta_q}\cdots s_{\beta_1})\]

로 정의되며, 이는 식으로 보면 복잡하지만 §호모토피, ⁋명제 6의 증명에서 등장하는 \(h_n\) 함수, 즉 prism \(\Delta^p\times \Delta^q\)를 simplex들로 쪼개주는 방법을 나타낸 것에 불과하다. 그럼 정리 9의 결과는 다음의 두 식

\[\AW\circ\EZ=\id_{(C(X)\otimes C(Y))_\bullet},\qquad \EZ\circ \AW\simeq \id_{C_\bullet(X\times Y)}\]

으로부터 나온다.

따라서 보조정리 8에 정리 9를 종합하면 다음의 결과를 얻는다.

따름정리 10 (Künneth) 위상공간 \(X,Y\)를 고정하자. 그럼 이들의 곱공간 \(X\times Y\)와 principal ideal domain \(A\)에 대하여, 다음의 short exact sequence

\[0 \rightarrow \bigoplus_{p+q=k}H_p(X;A)\otimes_AH_q(Y;A)\rightarrow H_k(X\times Y;A)\rightarrow \bigoplus_{p+q=k-1}\Tor_1^A(H_p(X;A),H_q(Y;A))\rightarrow 0\]

가 존재한다. 뿐만 아니라, 이 short exact sequence는 (non-canonical하게) split하며 따라서 다음의 isomorphism

\[H_k(X\times Y;A)\cong \left( \bigoplus_{p+q=k}H_p(X;A)\otimes_AH_q(Y;A)\right)\oplus \left(\bigoplus_{p+q=k-1}\Tor_1^A(H_p(X;A),H_q(Y;A)) \right)\]

이 존재한다.

물론, 이 결과와 정리 5를 사용하면 코호몰로지 버전의 퀴네트 공식을 얻을 수 있다.

---

참고문헌

[Hat] A. Hatcher, Algebraic Topology. Cambridge University Press, 2022.
[May] J. P. May, A concise course in algebraic topology.

---

1. 물론 우리는 이 pairing이 \(H^k(X;A)\)에서 \(\Hom(H_k(X),A)\)로의 homomorphism을 주는 것을 바랄 것이나, 상황이 이처럼 단순하지는 않고 숨겨진 torsion을 담고 있는 \(\Ext\) 항이 나와야 한다는 것을 명제 3로부터 알고 있다. ↩