§코호몰로지에서 언급한 것과 같이, acyclic models theorem은 §코호몰로지, ⁋정리 9의 원래 증명을 일반적인 방식으로 확장한 것으로, 비단 §코호몰로지, ⁋정리 9를 증명할 때뿐만 아니라 다양한 경우에 사용할 수 있다. 이번 글에서는 acyclic models theorem을 증명하고, §코호몰로지, ⁋정리 9의 증명을 포함한 몇몇 따름정리들을 소개한다.
Category with models
호몰로지 이론을 전개할 때 우리는 보통 $n$-simplex들을 사용하게 되며, 이들은 우리가 $\Top$의 임의의 원소들을 살펴보는데 도움이 된다. 이를 다음과 같이 정의로 삼을 수 있다.
정의 1 Category with models는 category $\mathcal{A}$와, $\mathcal{A}$의 object들의 모임 $\mathcal{M}$으로 이루어진 pair $(\mathcal{A},\mathcal{M})$을 뜻한다. 이 때, $\mathcal{M}$에 속하는 object들을 우리는 model들이라 부른다.
이 정의는 그 자체만으로는 별 영양가는 없다. 이제 우리는 다음을 정의한다.
정의 2 Category with models $(\mathcal{A},\mathcal{M})$이 주어졌다 하고, covariant functor $F_\bullet:\mathcal{A}\rightarrow \Ch_{\geq0}(\lMod{A})$가 주어졌다 하자.
- Functor $F_\bullet$가 acyclic on $\mathcal{M}$이라는 것은 각각의 $M\in\mathcal{M}$에 대하여, $H_i(F(M))=0$이 모든 $i>0$에 대하여 성립하는 것이다.
-
Functor $F_\bullet$가 free on $\mathcal{M}$이라는 것은 각각의 $n$에 대하여, 다음의 natural isomorphism
\[F_n(-)\cong \bigoplus_{M\in \mathcal{M}}\mathbb{Z}\Hom_\mathcal{A}(M,-)\]이 성립하는 것이다.
예를 들어, standard $n$-simplex들 $\Delta^n$들의 모임 $\mathcal{M}$을 model들로 갖는 category with models $(\Top, \mathcal{M})$을 생각하자. 그럼 각각의 $X\in \Top$마다 singular $n$-simplex들의 chain complex $C_\bullet(X)$을 대응시키는 functor $C_\bullet:\Top \rightarrow \Ab$는 acyclic on $\mathcal{M}$인 동시에 free on $\mathcal{M}$이다.
- $C_\bullet$이 acyclic on $\mathcal{M}$이라는 것은 §호몰로지, ⁋명제 11의 결과이다. 여기에서 functor $F_\bullet$이 $\mathcal{M}$ 위에서 acyclic하다는 조건은 $F_\bullet(X)$의 $0$번째 호몰로지가 $0$일 것을
요구하지는 않는다 는 것에 주의하자. - $C_\bullet$이 free on $\mathcal{M}$이라는 것은 정확히 각각의 $C_n(X)$들이 $\Delta^n \rightarrow X$로 생성되는 free abelian group이므로, 즉 $C_n(X)=\mathbb{Z}\Hom_\Top(\Delta^n,X)$이므로 자명하다.
Acyclic models theorem
이번 글의 메인 정리는 다음의 정리이다.
정리 3 (Acyclic models theorem) Category with models $(\mathcal{A},\mathcal{M})$과, 두 functor $F_\bullet, G_\bullet:\mathcal{A}\rightarrow \Ch_{\geq0}(\lMod{A})$이 주어졌다 하고 $F_\bullet$이 free on $\mathcal{M}$, $G_\bullet$이 acyclic on $\mathcal{M}$이라 하자. 그럼 두 functor
\[H_0(F(-)),H_0(G(-)): \mathcal{A}\rightarrow \lMod{A}\]사이의 임의의 natural transformation
\[f(-)_0:H_0(F(-)) \Rightarrow H_0(G(-))\]가 주어질 때마다, 적당한 natural transformation
\[f_\bullet(-):F_\bullet(-) \rightarrow G_\bullet(-)\]가 존재하여 $H_0(f)=f_0$이도록 할 수 있으며, 이러한 natural transformation $f$는 natural chain homotopy에 대하여 유일하게 존재한다.
즉, 호몰로지 레벨에서 정의된 $f(X)_0: H_0(F(X))\rightarrow H_0(G(X))$에서부터 시작하여, chain map $f_\bullet(X):F_\bullet(X)\rightarrow G_\bullet(X)$를 만들어야 한다. 이를 위해 우선 $f_\bullet(X)$의 $0$번째 성분 $f_0(X)$를 정의하자. 이는, $F_0(X)$이 free이므로, 각각의 $u:M\rightarrow X$이 어디로 옮겨지는지를 정의하는 것과 같다. 한편 다음의 commutative diagram
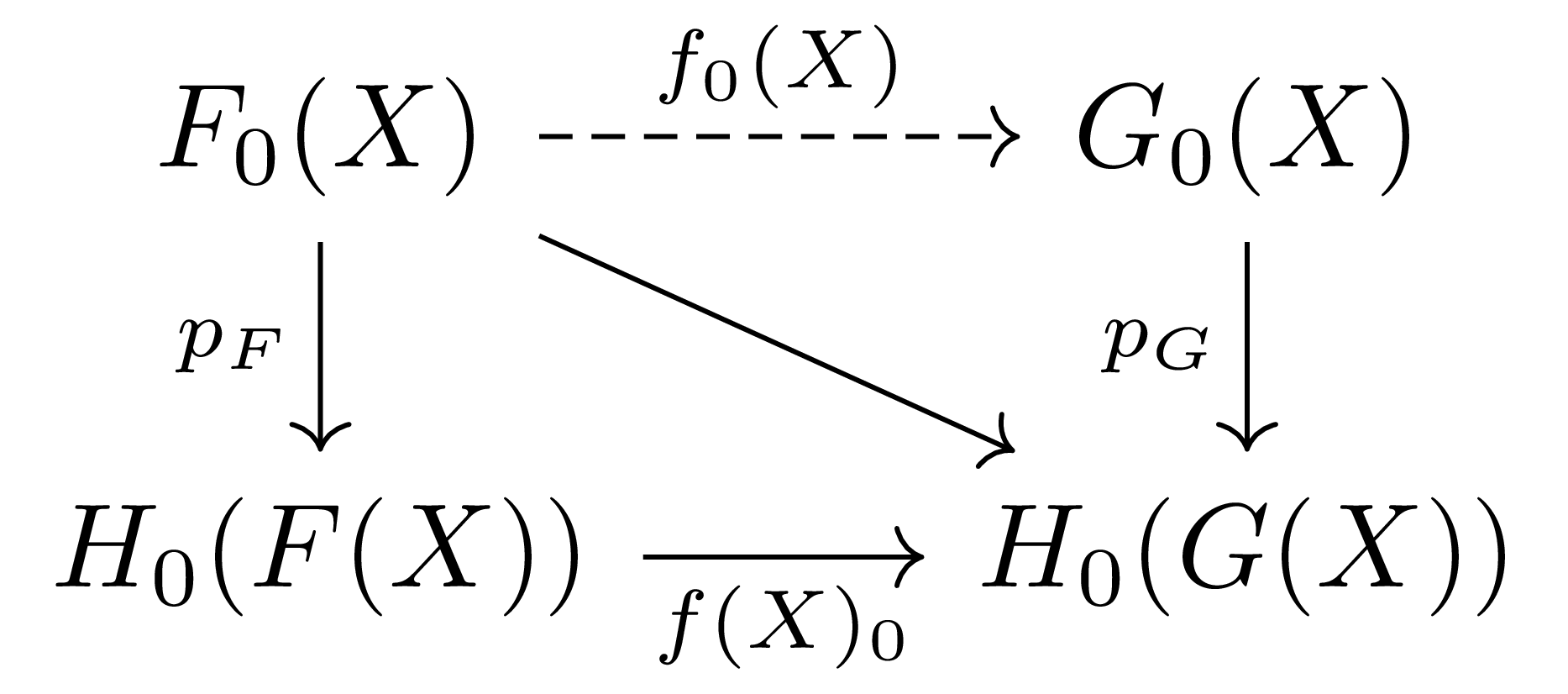
에 의하여, $F_0(X)\rightarrow H_0(G(X))$는 자명한 방식으로 정의되고, $p_G$가 surjective이므로 이로부터 lifting $F_0(X)\rightarrow G_0(X)$를 정의할 수 있다.
그러나 더 높은 차수에서 $f_\bullet(X)$를 정의하려면 약간의 문제가 있다. 귀납적으로 $f_{n-1}(X)$까지의 성분이 정의되었다고 하고 $f_n(X)$를 정의하자. 즉 다음의 diagram
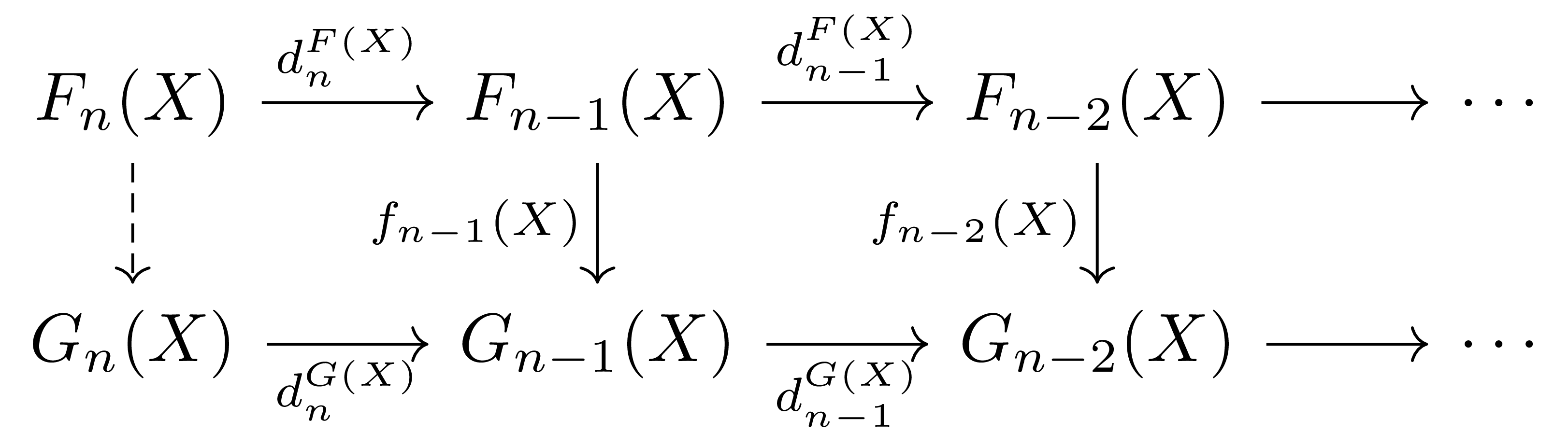
의 lifting을 정의해야하는데, 위의 상황과는 다르게 우리는 새로 정의한 $f_n(X)$가 다음의 commutativity 조건
\[d_n^{G(X)}\circ f_n(X)=f_{n-1}(X)\circ d_n^{F(X)}\]을 만족할 것을 요구해야 한다. 또 $f_n(X)$를 (위의 commutativity 조건이 없더라도) 어떻게 정의해야 할지도 명확하지 않다.
이를 해결하기 위해 $G$가 acyclic on $\mathcal{M}$이라는 조건을 사용한다. 우선 functor $F_n$이 free라는 것으로부터, 우리는 $f_n$을 model들 $M$ 위에서만 정의하면 된다는 것을 안다. 임의의 대상 $X$와 free module $F_n(X)$, 그리고 generator $u:M \rightarrow X$에 대하여 다음 diagram
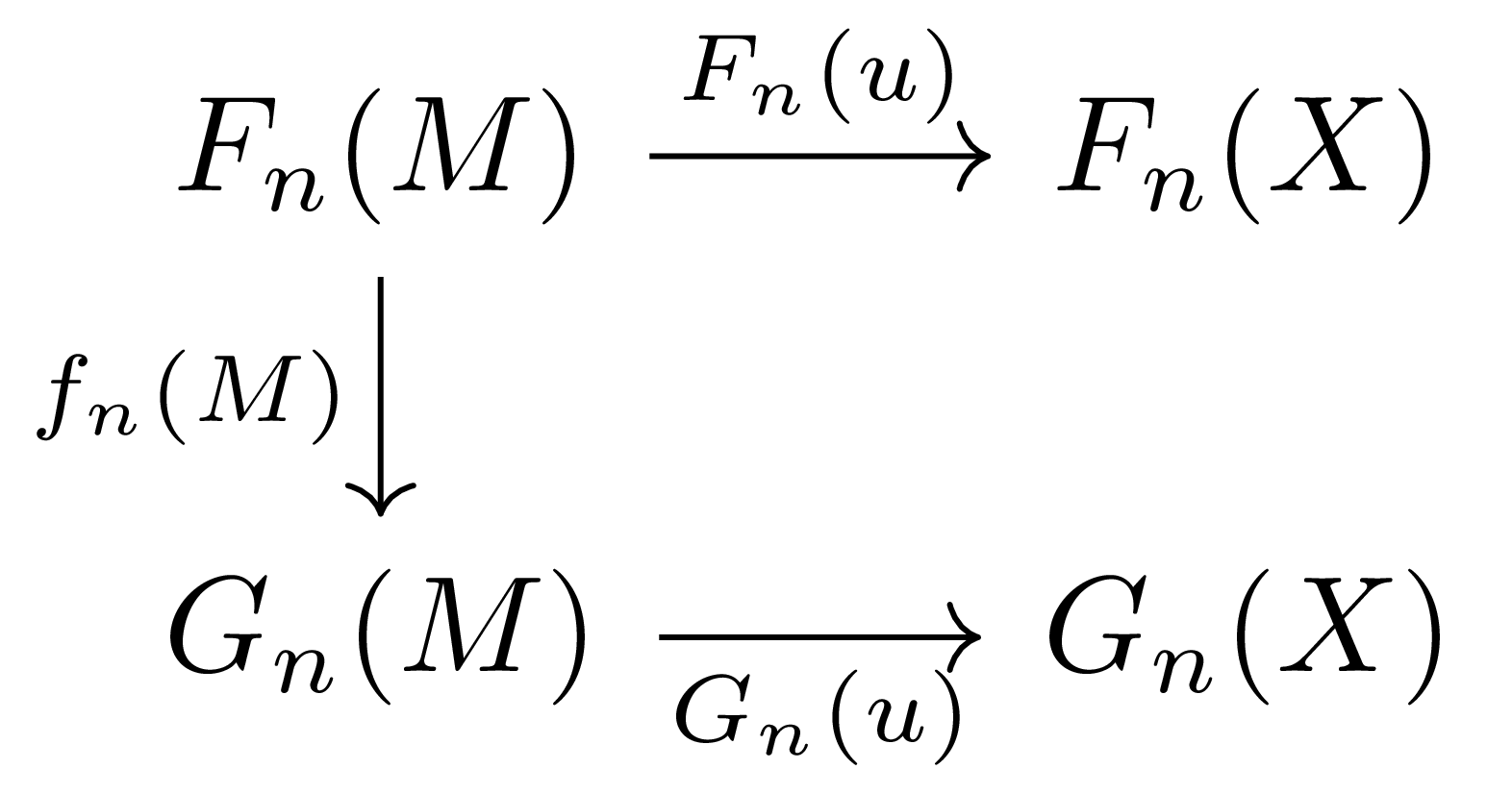
을 이용하면, $\id_M$에 해당하는 $F_n(M)$의 원소가 $F_n(X)$에서는 $u$가 되며, 그럼 $u$를 $(G_n(u)\circ f_n(M))(\id_M)$으로 옮겨주면 되기 때문이다. 이제 우리의 관심사를 model들로 옮겨놓고 나면, 우리가 해야할 일은 앞선 diagram
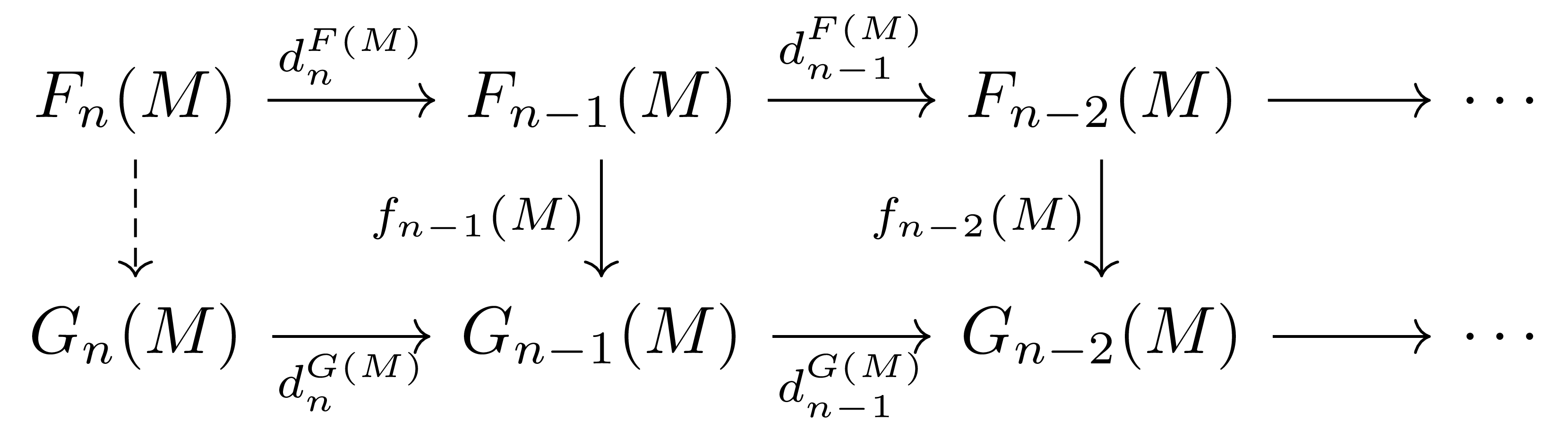
을 lift하는 것이다. 그런데 이제 임의의 $x_n\in F_n(M)$에 대하여,
\[0=(f_{n-2}(M)\circ d_{n-1}^{F(M)}\circ d_n^{F(M)})(x_n)=(d_{n-1}^{G(M)}\circ f_{n-1}(M)\circ d_n^{F(M)})(x_m)\]이므로 $G$가 acyclic on $\mathcal{M}$이라는 가정으로부터
\[f_{n-1}(d_n^{F(M)}(x_n))\in \ker d_{n-1}^{G(M)}=\im d_n^{G(M)}\]이고, 따라서 $d_n^{G(M)}(y_n)=f_{n-1}(d_n^{F(M)}(x_n))$을 만족하는 $y_n$을 찾을 수 있으며 이로부터 chain map $f_\bullet(M)$의 $n$번째 성분을 만들어줄 수 있다. 이 때 서로 다른 $y_n$의 선택은 서로 다른 lift $f_n$을 주며, 이들의 차이가 곧 chain homotopy를 정의한다.
Acyclic models theorem의 활용
Acyclic models theorem은 우선, 앞선 글에서 살펴본 퀴네트 정리를 증명할 때 사용된다. 두 위상공간의 pair로 이루어진 category $\Top^2$를 생각하고, 여기에서 $\Ch_{\geq 0}(\lMod{A})$로의 두 functor
\[C_\bullet(-\times -;A),\qquad C_\bullet(-;A)\otimes_A C_\bullet(-;A)\]를 생각하자. 이제 model $\mathcal{M}$을
\[(\Delta^p, \Delta^q)\in\Top^2\]들의 모임으로 잡으면, 이들은 모두 free on $\mathcal{M}$, acyclic on $\mathcal{M}$이다. 이제 다음의 함수
\[C_p(X;A)\times C_q(Y;A)\rightarrow C_{p+q}(X\times Y;A);\qquad (\sigma,\tau)\mapsto \sigma\times\tau\]가 $H_0$에서는 isomorphism인 것을 알 수 있고, 그럼 이 함수의 lifting이 Eilenberg-Zilber map, 그리고 이 함수의 inverse의 lifting이 Alexander-Whitney map이 된다.
비슷한 예시로, $\Top^2$에서 $\Ch_{\geq 0}(\lMod{A})$로의 네 functor
\[(X,Y)\mapsto C_\bullet(X\times Y;A),\quad (X,Y)\mapsto C_\bullet(Y\times X;A),\quad (X,Y)\mapsto C_\bullet(X;A)\otimes_AC_\bullet(Y;A),\quad (X,Y)\mapsto C_\bullet(Y;A)\otimes_AC_\bullet(X;A)\]를 생각하면, 이들 사이의 자명한 함수들을 생각할 수 있으며 이를 정리 3을 이용하여 lift하면 $\Ch_{\geq0}(\lMod{A})$에서의 commutative diagram
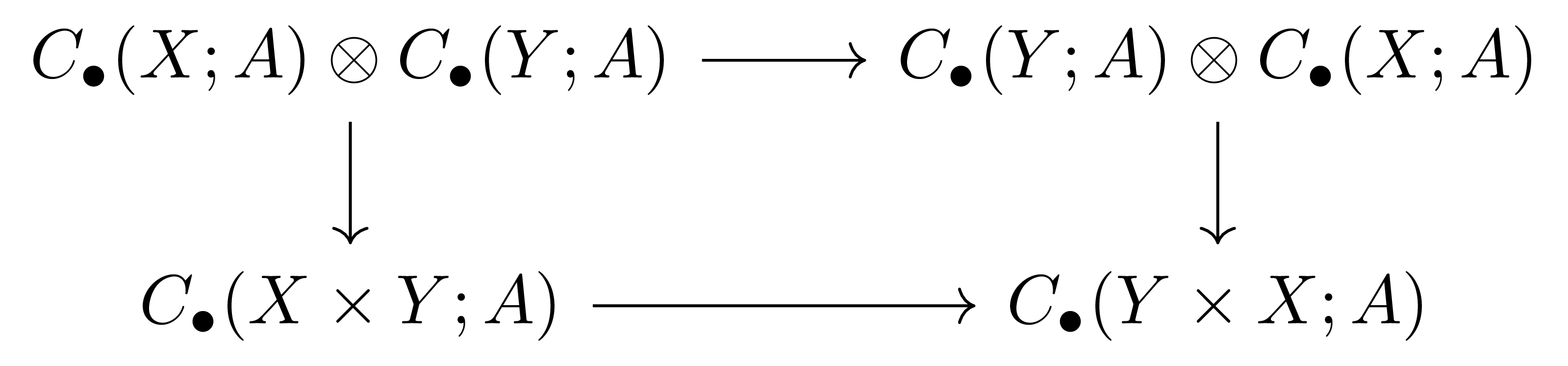
을 얻는다.
참고문헌

댓글남기기